一类扩展交错级数的收敛判别法
2015-08-24钟艳林闽南理工学院福建泉州362700
钟艳林(闽南理工学院,福建 泉州 362700)
一类扩展交错级数的收敛判别法
钟艳林
(闽南理工学院,福建 泉州 362700)
无穷级数是高等数学的重要组成部分,通过对交错级数的扩展得到一类新的级数,对新级数加括号后并将每个括号看作一个整体就得到一个交错级数,通过证明得出判断新级数的判别方法。
级数;收敛;交错级数;判别法
无穷级数是高等数学的重要组成部分,它是表示函数、研究函数性质以及进行数值计算的一种重要的数学工具,在电学、力学及计算机辅助设计等方面有着广泛的应用。无穷级数由数项级数和函数项级数两部分构成。设有数列 u1,u2,…,un,…,则式子…称为数项级数。级数
的前n项之和为Sn,即,称 Sn为级数的部分和,当n=1,2,…时,则得到一个部分和数列:若部分和数列的极限存在,即,则称级数收敛,否则称级数发散[1]。
判断一个数项级数是收敛还是发散,我们有著名的柯西收敛原理:级数收敛的充分必要条件是:对任意给定的正数ε,总存在N,使得当n>N时,对于任意的自然数p=1,2,…,恒成立。在一般情况下,利用级数的的定义或柯西收敛原理来判断一个级数是否收敛通常难度较大,也有一定的局限性,因此介绍一些判断级数是否收敛的方法就十分必要。若级数中的各项均非负,即,则称该级数为正项级数,判断正项级数是否收敛,我们有好多判别法,如比较判别法、达朗贝尔比值判别法、柯西判别法[2]、柯西积分判别法等[3]。若级数中正、负项交替出现,即其中称该级数为交错级数,判断交错级数我们有莱布尼茨判别法。本文将讨论一类级数:该级数由正项和负项合成,但正项与负项不是交替出现,例如,这个级数第1, 2,3项为负,而第4,5,6,7,8项为正。众所周知,对于一般的级数而言,将一个级数加括号后作成一个新级数,即使加括号后得到的新级数收敛,我们也没办法推出原级数是收敛的[4],例如:级数,若将此级数第1,2项加括号,第3,4项加括号,依此类推下去得到一个新级数收敛,可原级数明显是发散的。但如果加括号后的新级数每个括号里的项都同号且收敛的话,那原级数是否收敛呢?
定理1:若级数的项加括号后,每个括号里的所有项都有相同的符号并且收敛,则原级级数一定收敛。
收
当n(k=1,2,…)时,所有的 un的符号都相同,现记
Uk,现对原级数
又由
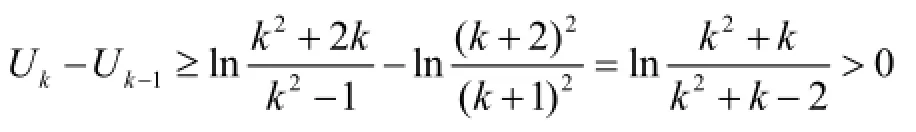
[1]同济大学数学系.高等数学[M].高等教育出版社,北京,(2007)
[2]杨钟玄.正项级数敛散性的一个新判别法[J].四川师范大学学报(自然科学版).2005(06):41-44.
[3]吴慧伶.正项级数收敛性判别的一个推广[J].丽水学院学报. 2006(05):24-27.
[4]苏翃;邱利琼;王大坤;董建.一类交错级数的收敛定理[J].大学数学.2006(05):143-145.
[5]范新华.关于交错级数敛散性判别法的一些探讨[J].常州工学院学报.2007(05):57-59.
(责任编辑:雷君)
Method of Discrimination a class series
ZHONG Yan-lin
(Minnan University of Science and Technology,Quanzhou Fujian 362700)
Infinite series is an important part of higher mathematics,through the alternating series of extensions to get a new kind of series,the new series in parentheses after each bracket as a whole will get an alternating series,through come to judge the new series prove discrimination method.
Series;Convergence;Staggered series;Method of discrimination
O29
A
10.3969/j.issn.1672-7304.2015.03.037
1672-7304(2015)03-0089-02
钟艳林(1980-),男,湖南衡阳人,讲师,研究方向:数学与应用数学。
福建省中青年教师教育科研项目资助(JB14108)。
