动能定理的解法例析

陈　群

(江苏省南京市第二十九中学,江苏　南京　210036)



动能定理的解法例析

陈群

(江苏省南京市第二十九中学,江苏南京210036)

摘要：本文针对高中物理中变力、多过程等复杂问题,利用动能定理来解决物理问题,让学生学会分析运动过程，并且能够体会动能定理解题的清晰巧妙，文中以实例的形式进行了分析.

关键词：动能定理;变力做功;多过程问题

动能定理是力学研究中的重要原理之一,它反映了做功与动能之间的关系,给出了过程量功与状态量动能之间的标量运算式.

动能定理表述为:合外力做的功等于物体动能的变化,表达式为W合=ΔEk.也可以表述为:外力对物体做的总功等于物体动能的变化.实际操作时,后一种表述不必求合力,特别是在研究多过程的问题时,当受力有变化的情况下,只要把各个力在各个阶段所做的功都代数加起来即可.

学生在最初接触动能定理时,更喜欢用牛顿运动定律解题,但其实用动能定理解题一般更为简捷,特别是在处理变力问题及多过程问题上.故在教学过程中,需要注意恰当的引导.

1应用动能定理巧求变力的功

例1:质量为5×105kg的机车,以恒定的功率沿平直轨道行驶,在3min内行驶了1450m,其速度从10m/s增加到最大速度15m/s.若阻力保持不变,求机车的功率和所受阻力的数值.

解析:本题的受力分析并不困难(如图1),但机车的牵引力是变力,若直接用牛顿运动定律计算不可行,故可引导学生运用动能定理.在机车速度从10m/s增加到15m/s的过程中,重力和支持力不做功,牵引力F对机车做正功,阻力对机车做负功.

图1

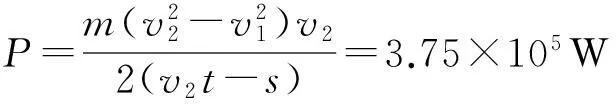
例2:如图2所示,粗糙的1/4圆弧的半径为0.45m,有一质量为0.2kg的物体自最高点A从静止开始下滑到圆弧最低点B时,然后沿水平面前进0.4m到达C点停止.设物体与轨道间的动摩擦因数为0.5(g=10m/s2),求:物体在圆弧轨道上克服摩擦力所做的功.

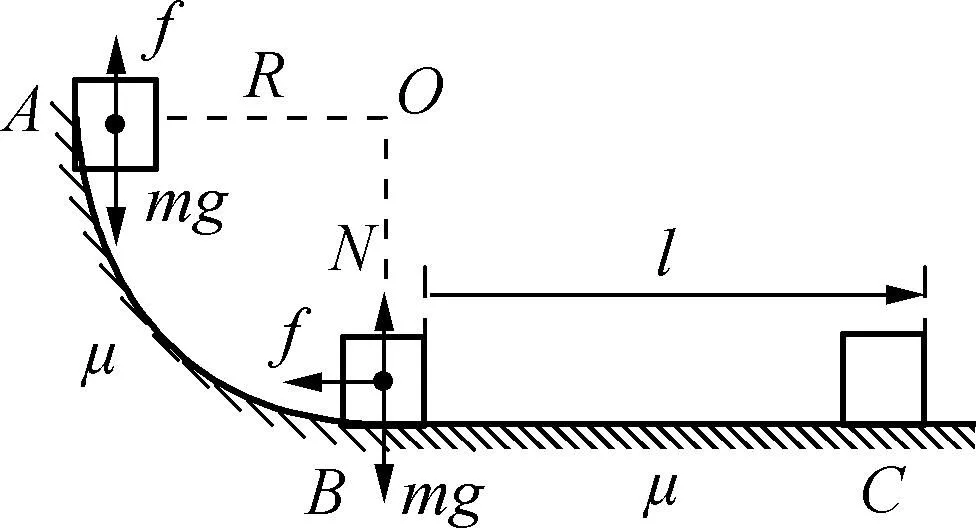
图2

小结:在教学过程中,可以通过以上类似的问题,让学生体会当所研究的问题中只有一个变力做功,或者有多个力做功,但其中有一个力是变力做功时,选用动能定理解题,可化难为易.

2应用动能定理解多过程问题

例3:固定的轨道ABC如图3所示,其中水平轨道AB与半径为R/4的光滑圆弧轨道BC相连接,AB与圆弧相切于B点.质量为m的小物块静止在水一平轨道上的P点,它与水平轨道间的动摩擦因数为μ=0.25,PB=2R.用大小等于2mg的水平恒力推动小物块,当小物块运动到B点时,立即撤去推力(小物块可视为质点).求小物块沿圆弧轨道上升后,可能达到的最大高度H.

3.实施多证合一，开展联合监管。加强与工商、环保公安等部门的合作，成立联合执法检查组，对辖区范围内纳税人开展联合检查、联合管理；与公安经侦部门建立信息互通机制，及时通报偷逃骗税等违法案件。开创多部门联合管理的新局面，有效防止纳税人虚开发票后走逃或失联，企业违规退税、骗税，造成税款流失。

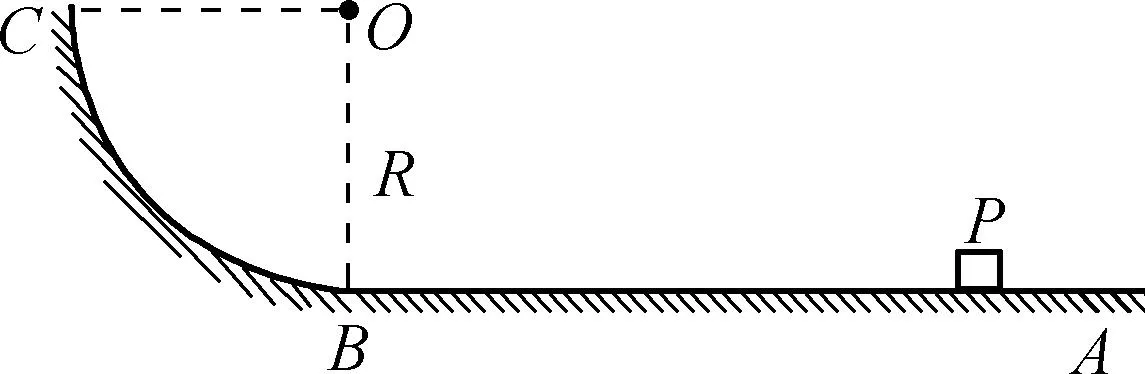
图3

解析:本题若用牛顿运动定律解题是可以完成的,但涉及的公式较多,需要求加速度、时间等物理量.运用动能定理解题可以从过程出发,避开小的细节,更为简便.

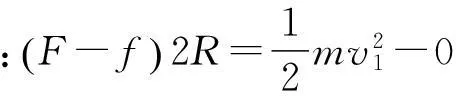
物块由C点竖直上抛,根据动能定理:

解法二：可以用整体法,更为方便，对全过程求解:P→C,根据动能定理:F·2R-f·2R-mgh=0,其中F=2mg,f=μmg,所以H=3.5R.

例4：如图4所示,倾角为θ=45°的斜面固定于地面,斜面顶端离地面的高度h0=1m,斜面底端有一垂直于斜面的固定挡板.在斜面顶端自由释放一质量m=0.09kg的小物块(视为质点).小物块与斜面之间的动摩擦因数μ=0.2.当小物块与挡板碰撞后,将以原速返回.重力加速度g=10m/s2.试求:

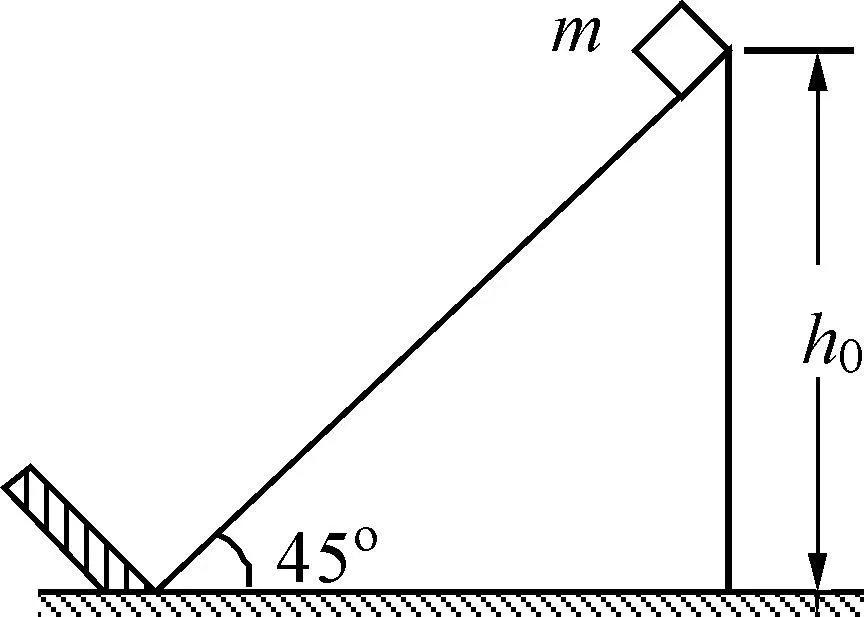
图4

(1) 小物块与挡板发生第一次碰撞后弹起的高度;

(2) 小物块从开始下落到最终停在挡板处的过程中,小物块通过的总路程.

(1) 在物块自起点至弹起到最高点的全过程中，根据动能定理,有:

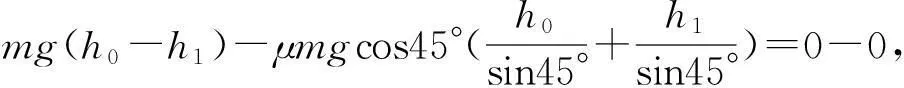
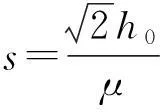
小结:在教学过程中,可以适当地选择一些多过程的问题,激励学生讨论,让学生从中感悟物体在某个运动过程中包含有几个运动性质不同的小过程(如加速、减速的过程),此时可以分段考虑,也可以对全过程考虑,但如能对整个过程利用动能定理列式，则会使问题简化.

3对多物体系统应用动能定理

例5：质量为M、厚度为d的方木块,静置在光滑的水平面上,如图5所示,一子弹以初速度v0水平射穿木块,子弹的质量为m,木块对子弹的阻力为Ff且始终不变,在子弹射穿木块的过程中,木块发生的位移为L.求子弹射穿木块后,子弹和木块的速度各为多少？

图5

解析:牛顿运动定律对解决系统的运动问题相对复杂,尤其是系统内的物体加速度不同的时候.但从能量的角度就容易处理了.本题可以不去求解子弹和木块的加速度,直接用动能定理梳理出各自的动能变化.以地面为参考系,子弹受力如图6左图所示,由题知子弹的初速度为v0,对地位移为s=L+d,阻力为Ff.对于子弹射穿木块的过程，由动能定理得：

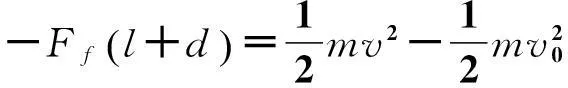
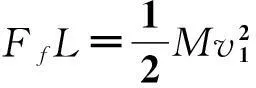
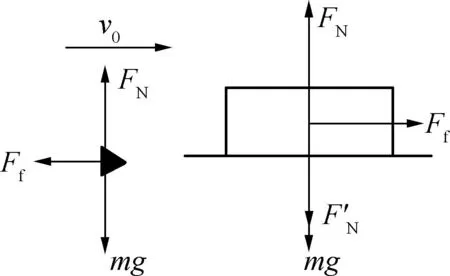
图6

例6：如图7所示,在水平桌面的边角处有一轻质光滑的定滑轮K,一条不可伸长的轻绳绕过K分别与物块A、B相连,A、B的质量分别为mA、mB,开始时系统处于静止状态,现用一水平恒力F拉物块A,使物块B上升.已知当B上升距离为h时,B的速度为v,求：(1) 动摩擦因数为多大？(2) 撤去拉力后,物块A还能滑行多远？(重力加速度为g)

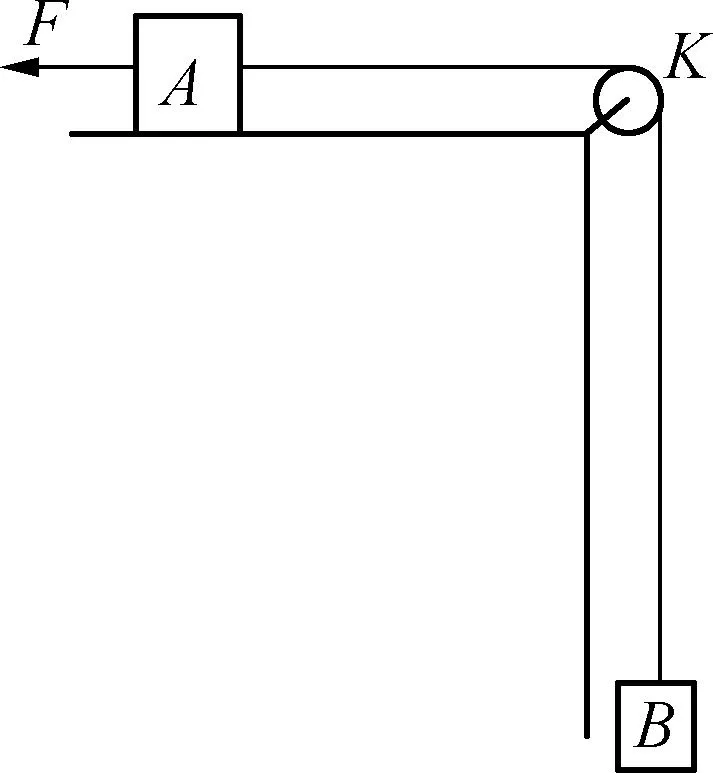
图7

解析:针对多物体系统采用动能定理解题，通常比较便利.无需单独分析物块各自的加速度,从系统动能的变化入手,可直接得到结果.

(2)撤去拉力后,A、B以共同的加速度a减速运动,直到速度为零,对系统全过程,由动能定理:Fh-μmAg(s+h)-mBg(s+h)=0-0,联立代入数据解得:s=0.5m.

小结:在教学过程中,可以选择一些多物体系统问题,让学生从中领会应用动能定理时,要确定好研究对象,找出始、末位置及其对应的动能,确定好研究过程,进行受力分析,并确定过程中各个力做功的情况,以便找到总功.学会应用动能定理解决物理问题的解题思路,可提升学生思维能力、分析问题和解决问题的能力.