列车荷载作用下渗漏隧道的长期非线性固结

曹 奕，蒋 军，谢康和，陈炜昀3

（1.中国电建集团华东勘测设计研究院有限公司，310014杭州；2.浙江大学建筑工程学院，310058杭州；3.南京工业大学岩土工程研究所，210000南京）

列车荷载作用下渗漏隧道的长期非线性固结

曹 奕1，2，蒋 军2，谢康和2，陈炜昀3

（1.中国电建集团华东勘测设计研究院有限公司，310014杭州；2.浙江大学建筑工程学院，310058杭州；3.南京工业大学岩土工程研究所，210000南京）

为研究列车荷载对地铁周边土体长期非线性固结的影响，以及其与隧道渗漏的共同作用，将列车荷载等效为矩形循环荷载，采用经典的土体非线性固结理论，以及衬砌与土体相对渗透性系数，得出列车荷载作用下局部渗漏隧道的非线性固结解析解.通过本文预测值与上海地铁实测数据的对比，验证了解析解的合理性.分析结果表明：列车荷载加剧了隧道上方地表长期沉降，衬砌渗漏程度越大，沉降增加量越大.本文解析解能较好模拟隧道周边土体的长期固结特性，为预测地铁隧道长期运营导致的地表沉降提供一个较为合理有效的方法.

列车荷载；盾构隧道；非线性固结；解析解；衬砌渗漏

饱和软土地区的地铁在运营过程中，列车振动荷载的长期作用将导致隧道轴向的变形、地面沉降的加剧，对地铁运营的耐久性和周边环境造成不良影响.许多学者就此问题进行了研究，文献［1－4］等分别采用动三轴试验等方法确定土体的动弹性模量，采用有限元计算等数值模拟方法计算了饱和软土地区列车振动荷载作用下地基变形及地面沉降的经验模型、数值解或解析解.这些研究均未考虑隧道渗漏条件造成的地表附加沉降.而在饱和软土地区，由于隧道衬砌内外存在一个较大的水头差，且衬砌管片接头的手孔、螺栓孔等处存在不同程度的渗漏，由此隧道在其周边土体中引入了一个新的透水边界.文献［5－9］的研究表明这将对土体内的孔压发展和变形产生较大影响，盾构隧道衬砌局部渗漏特性对地表长期沉降的影响不容忽视.

为研究隧道周边土体在列车荷载作用下的长期固结沉降，作者在文献［10－11］中将隧道衬砌理想化为完全透水和完全不透水两种极端情况，得到了衬砌渗漏对地铁隧道周边土体长期固结影响的上下限.本文采用文献［12］提出的衬砌与土体相对渗透性系数模拟隧道衬砌的局部渗漏特性，采用文献［13－15］提出的非线性固结理论建立土体的固结控制方程，通过将列车荷载等效为矩形循环荷载，推导相应的孔压和土体沉降解析解，然后通过等效矩形循环荷载参数的调整，分析列车荷载对土体固结、地表沉降的影响，并通过与上海地铁1号线实测数据的对比，验证解析解的合理性.

1 问题描述

1.1 基本假定

对于饱和软土中考虑衬砌透水的隧道周边土体的非线性固结问题，采用图1计算简图.隧道半径为r，埋深为h，坐标原点位于隧道正上方地表处.综合文献［13－15］对土体非线性固结所作的假设和隧道周边土体的固结问题，基本假定：

1）隧道纵向长度足够长，满足平面应变条件；

2）洞周土体视作带圆孔的半无限空间；

3）隧道周围土体均为各向同性饱和多孔介质，土体渗透性的变化服从e－lg k关系，压缩性的变化符合e－lgσ关系［11－13］；

4）土颗粒和孔隙水不可压缩，孔隙水流动服从达西定律，地表及无穷远处的超静孔压为零；

5）变形为小变形，不计变形对坐标的影响；

6）地基内各点土体自由变形，不受土体自身及隧道成拱作用影响；

7）盾构施工只在土体中引起超孔压，土体竖向总应力不变.

图1 半无限空间中隧道计算简图

1.2 列车荷载的简化

本文将列车荷载简化为矩形循环荷载，加载形式见图2.假设列车长度L，运行速度v，则列车荷载单次加载时间ta＝L／v，间隔时Δt，等效荷载最大值qu，列车运行时刻表以一天为周期.

列车荷载的函数表达式为

式中：t0为每天列车开始运营的时间，Δt为列车间隔时，n为列车单日运营序数.

图2 列车荷载示意

2 问题求解

2.1 控制方程

依据文献［13－15］的假定，以及文献［11］对控制方程的推导，由自由应变条件下的基本假定得到饱和土体连续方程：

式中：e为土体孔隙比，e0为土体的初始孔隙比，ks为土体的渗透系数，εv为土体中某点的体应变，γw为水的重度，Δu为超孔隙水压力.

假定土体初始渗透系数为ks0，初始有效应力σ′0，由文献［13－15］，土体的压缩性和渗透性服从经验公式：

式中：ks0为土体的初始渗透系数，Cc为压缩指数，Ck为渗透指数，σ′0为初始有效应力，σ′为有效应力.

由式（4）、（5）可得

式中mv0＝Cc／(1 ＋e0)σ′0ln10为初始土体压缩系数，mv为土体压缩系数.

将mv0代入式（7）可得

由有效应力原理且总应力不变，则有由于非线性方程求解困难，作与文献［11］类似的假定：土体压缩性和渗透性同步变化，即Cc／Ck＝1，将式（4）、（6）、（9）代入式（1），可得控制方程为

令

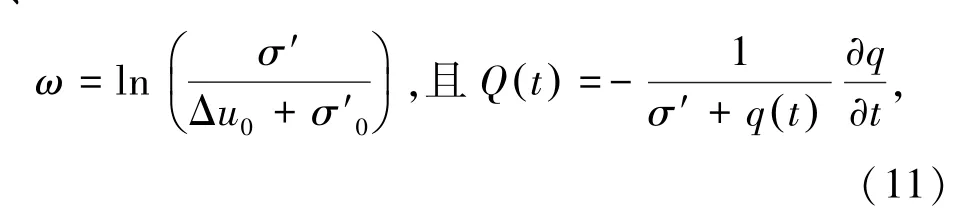
则控制方程（10）简化为

式中Cv0＝ks0／(γwmv0)为固结系数.

2.2 保角变换

因为在x－y坐标系内求解上述问题十分困难，故将复平面z＝x＋i y中隧道边界外的半无限空间通过保角变换ω（ζ）映射为ζ平面内的一个环域，其中半径为1的圆环外边界为原Z平面中地表，半径为R的圆环内边界为隧道衬砌边界，见图3.采用文献［16］提出的保角映射函数：

式中：h为隧道埋深，R为ζ平面内隧道边界.其中

此时控制方程（12）变为

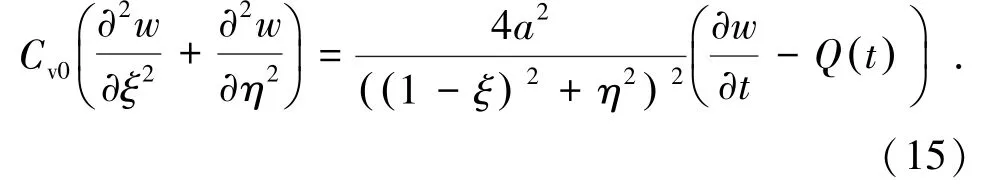
图3 保角映射后的区域

2.3 局部渗漏边界及初始条件

采用文献［17］的假设，在初始时刻隧道外壁附近土体的超孔压已知为q的情况下，土体中由于盾构推进等施工因素所引起的超孔隙水压力Δuc，隧道渗漏引起的漏水，可近似认为隧道外壁处的超静孔压是均匀的，而在地表及无穷远处的超静孔压为零.

盾构隧道在土体中引入了新的渗流边界，当达到新的渗流平衡状态时，隧道周边土体中静水孔压的减小量，与隧道施工造成的超孔压的消散量，共同构成了渗流固结稳定后的总有效应力增量，即

式中：Δσf为固结完成时总有效应力增加量，Δu0为固结完成时的孔压总消散量，u0为隧道开挖前土体中的静水孔压，us为隧道周边土体达到稳定渗流状态时的孔隙水压力.

根据文献［18］提出单位时间内流入单位长度隧道衬砌的渗流量解析解为

式中：Qt为单位长度隧道在单位时间内的渗流量.kc为衬砌的渗透系数，ksf最终固结完成时土体的渗透系数，r1和r2分别为隧道内外半径，uT为最终固结完成时衬砌与土体边界面上孔压.土体中离隧道中心距离为r＝处，单位时间内沿单位隧道长度土体的渗流量解析解为

由单位时间内单位隧道长度的土体中经过不同渗流边界面的渗流量相等，可得稳定渗流时土中的孔压分布为

式中uT可从式（18）得到.

据文献［12］，引入考虑隧道衬砌尺寸效应的土与衬砌相对渗透性系数 κ，其与超孔压的方向导数有

将式［6］代入式［21］，可得

式中：κ0＝kc／(ks0r2ln（r2／r1）)为初始相对渗透性系数.由于非线性固结过程中，κ发生了很大变化，下文中以κ0表示隧道局部渗漏特性.

从而可得局部渗漏边界条件和初始条件：

2.4 问题求解

采用分离变量法求解上述控制方程和边界条件，令ω（ρ，θ，t）＝ω（ρ，θ）·T（t）代入控制方程：

求解上述方程，可得

其通解为

式中：J0（λχ）为 零阶 Bessel函数，N0（λχ）为零阶Neumann函数，A、B为待定系数，由边界条件确定.

采用局部渗漏边界条件直接求解式（26）中的待定参数存在很大困难，故本文采用逐步递推法：将整个非线性固结过程划分为若干个等时间长度为ΔT的阶段，考虑地铁列车的运营周期，取ΔT＝1 d.以Δui表示第i阶段的超孔压，相应地Δui0，σ′i0分别为第i阶段初始超孔压和初始有效应力，κi0为第i阶段的初始相对渗透性系数.

将边界条件代入通解可得

式中：λij为固结过程中第i阶段的第j个特征值，且

其中Ω＝1＋R2－2R cosθ，ζ＝R( R －cosθ).

由方程组（27）可知，要得到Ai、Bi的非零解，λij须满足特征方程：

式（29）为关于λij的特征方程，记作f（λij）＝0，其为关于λij的偶函数，可不考虑负根，用逐步搜索的办法得到f（λij）＝0由小到大的无数多个正根序列为{ λi1，λi2，…，λij，…，λin}.

可得

式中Gij是由边界条件决定的待定系数，Ωρ＝1＋ρ2－2ρcosθ.

将特征值λij代入式（24），可得

由关于t的Laplace变换可得

式中T（0）＝1，且

对式（31）作Laplace逆变换，可得到Tij，由此可得

由式（11），可得孔压表达式为

由有效应力原理且总应力不变，可得第i时间段任意时间点的有效应力σ′i，由式（3）～（5）可得第i＋1时间段的衬砌与土体的初始相对渗透性系数为

式中：kc为初砌渗透系数，ks，i第i时间段土体的渗透系数，ks0，i为第i时间段土体的初始渗透系数.之后便可以进行第i＋1时间段土体超孔压的迭代求解.

2.5 待定系数Gij的确定

根据Bessel函数的性质，特征值不同的特征函数在区间［R，1］上为加权正交：

由初始条件式和Wn（χ）的加权正交性得到

2.6 按超静孔压定义的固结度

第i时间段按超静孔压定义的土体平均固结度为

2.7 固结沉降的求解

同时根据广义胡克定律和平面应变假设，可得第i时间段土中任意一点某一时刻的竖向应变为

式中K0为静止土压力系数，ν为土体泊松比.

由此可得第i时间段某一时刻地表某处的沉降为

3 隧道周边土体长期固结沉降的预测

为分析列车荷载以及隧道局部渗漏状态对周边土体长期固结性状的影响并验证本文解析解的合理性，取文献［19］提供的上海地铁1号线测点的土性参数和实测沉降数据，进行沉降预测和对比分析.

3.1 计算参数

上海地铁1号线全长14.6 km，隧道直径6.2 m，上覆土层厚度6～8m，位于软弱的饱和淤泥质粘土层中.计算断面处埋深11 m，盾构隧道外径6.2 m，内径5.5 m.等效均质土体的初始渗透系数为 5.14× 10－9m／s，初始压缩指数为0.25，初始孔隙比为1，泊松比ν为0.36，静止土压力系数K0为0.43.根据文献［20］，由盾构施工在隧道周边土体中引起的超孔压q取为30.3 kPa.取3种隧道局部渗漏状态，以衬砌与土体相对渗透性系数表示，分别为κ0＝∞即衬砌完全渗漏，κ0＝0.018即当衬砌渗透性接近于隧道实际渗漏情况（衬砌渗透系数 kc约为 3.89×10－11m／s［21］），κ0＝0即隧道衬砌完全不渗漏.列车荷载情况采用文献［22］提供的上海地铁列车荷载数据，列车荷载qu约为70 kPa，地铁运行时速80 km／h，地铁列车车厢长度约为22m，按照每列车5节车厢，则式（1）中单次列车荷载作用时间ta为4.95 s，列车间隔时Δt取为3min，每日运行次数n取320次.

3.2 土体固结情况

等效矩形循环荷载峰值 qu分别为 0 kPa和70 kPa时，不同衬砌渗漏条件下土体平均固结度的发展情况见图4.

图4 土体平均固结度与时间的关系

图4表明，隧道局部渗漏程度的不同，将使隧道周边软土固结度的发展表现出很大的差异性.在不考虑列车荷载即取qu＝0 kPa的情况下，且κ0＝∞时，土体的非线性固结在700 d接近完成；当衬砌为实际的局部渗漏状态即κ0＝0.018时，在1 600 d接近完成；而隧道处于完全不渗漏状态即κ0＝0时，2 200 d接近完成.这也证实了隧道衬砌相对与土体的渗漏特性，很大程度上决定了隧道周边土体的固结速度.

而列车荷载取qu＝70 kPa时，由于列车荷载作用下累积孔压的增长和消散，不论隧道处于何种渗漏状态，周边土体固结度的发展均比相应渗漏条件下qu＝0 kPa（即不考虑列车荷载）时缓慢.因此，在分析隧道周边土体的长期非线性固结时，考虑列车荷载以及隧道衬砌与土体的相对渗透性对于土体固结的影响是合理而且必要的.

3.3 隧道中心线处地表沉降发展情况

等效矩形循环荷载峰值 qu分别为 0 kPa和70 kPa时，不同衬砌渗漏条件下的隧道中心线处地表总沉降量随时间的发展情况及上海地铁1号线的实测沉降值，见图5.由列车荷载导致的地表沉降增加量见图6.

由图5可知，当qu为70 kPa且局部渗漏时，在地铁运营前期（0～80 d），本文解析解的预测沉降值略小于实测沉降值，其差异约4%～6%，而在100 d以后，本文预测沉降值同实测沉降值十分接近，其差异在3%以内.当考虑列车荷载时，考虑衬砌局部渗漏的非线性固结解析解较为符合土体的长期固结特性.而在相同的列车荷载条件下，隧道处于实际衬砌渗漏条件即κ0＝0.018时，非线性固结解析解得到的沉降预测值均位于完全渗漏状态和完全不渗漏状态获得的预测值范围内.实测沉降值，要远大于列车荷载为零时本文提出的解析解预测值.

图5 地表沉降与时间的关系

图6 列车荷载导致的地表沉降与时间的关系

从图5可得出与上小节类似的结论：衬砌局部渗漏为隧道周边土体提供了一个新的边界，加速了土体的固结；当最终渗漏稳定时，衬砌的局部渗漏增大了静水孔压消散量，从而加剧地表的长期沉降.

由图6可知各个隧道渗漏条件下，与列车荷载为零时相比，qu为70 kPa时，隧道中心处地表沉降均有不同程度的增加.沉降增加量与衬砌渗漏条件有关，渗漏程度越大，沉降增加量越大.这表明，列车荷载与隧道局部渗漏条件相耦合，共同影响了长期固结沉降.与文献［2］采用不排水条件下累积孔压消散模型相比，本文采用局部渗漏边界条件能够更好预测地表固结沉降.

3.4 地表沉降速率发展情况

等效矩形循环荷载峰值 qu分别为 0 kPa和70 kPa时，不同衬砌渗漏条件下的隧道中心线处地表总沉降速率随时间的发展情况见图7，由列车荷载作用而增加的地表沉降速率见图8.

图7中，在经历了固结初期沉降速率的快速下降后，在200 d左右，不同渗漏条件下的沉降速率趋于一致，其后κ0衬砌与土体的相对渗透性越小时，其沉降速率的减少越为缓慢.隧道渗透性越差，固结后期的沉降增加量越大.实测沉降速率的下降趋势同实际局部渗漏条件下本文解析解预测值趋势较为一致.隧道衬砌相对土体的渗透性越大，隧道周边软土在固结初期（0～200 d）的沉降速率越大，这一现象证实了：隧道本身作为一个新的排水边界加速了土体的固结沉降，而列车荷载的加载，加快了地表沉降的发展.

图7 地表沉降速率与时间的关系

图8 列车荷载导致的地表沉降速率与时间的关系

图8表明：当κ0＝∞时，列车荷载导致的沉降速率在固结初期可达0.12 mm／d；当κ0为0.018时，沉降速率最大值可达0.07mm／d；相应地，当κ0＝0时，其值为0.02 mm／d.这表明隧道局部渗漏程度越大，列车荷载导致的地表沉降速率越大.

4 结 论

1）施加70 kPa的列车荷载比未施加列车荷载时，地表沉降均有不同程度增加.沉降增加量与隧道衬砌渗漏条件有关，渗漏程度越大，沉降增加量越大.

2）采用衬砌与土体相对渗透性系数能够有效模拟隧道局部渗漏特性，并通过与实测沉降数据的对比验证了本文解析解的合理性.

3）隧道衬砌的局部渗漏通道，为周边土体的固结提供一个新的排水边界，与列车荷载相耦合，共同影响了地表沉降的长期发展.

［1］唐益群，栾长青，张曦，等.地铁振动荷载作用下隧道土体变形数值模拟［J］.地下空间与工程学报，2008，4（1）：105－110.

［2］刘明，黄茂松，李进军.地铁荷载作用下饱和软粘土的长期沉降分析［J］.地下空间与工程学报，2006，2（5）：813－817.

［3］张学钢，黄阿岗，郭旺军.列车荷载长期作用下隧道地基固结变形的数值分析［J］.铁道工程学报，2011（4）：22－26.

［4］赵春彦，周顺华，袁建议.地铁荷载作用下叠交隧道长期沉降的半解析法［J］.铁道学报，2010，32（4）：141－145.

［5］MAIR R J.Tunnelling and geotechnics：new horizons［J］.Geotechnique，2008，58（9）：695－736.

［6］张冬梅，黄宏伟，杨峻.衬砌局部渗流对软土隧道地表长期沉降的影响研究［J］.岩土工程学报，2005，27（12）：1430－1436.

［7］刘印，张冬梅，黄宏伟.盾构隧道局部长期渗水对隧道变形及地表沉降的影响分析［J］.岩土力学，2013，34（1）：290－298

［8］WARD W H，PENDER M J.Tunnelling in soft ground：general report［C］／／Proceedings of the 10th International Conference on Soil Mechanics and Foundation Engineering.Stockholm：［s.n.］，1981，4：261－275.

［9］SHIRLAW JN.Observed and calculated pore pressures and deformations induced by an earth balance shield：discussion［J］.Canadian Geotechnical Journal，1995，32（1）：181－189.

［10］CAO Y，JIANG J，XIE K H，et al.Analytical solutions for nonlinear consolidation of soft soil around a shield tunnel with idealized sealing linings［J］.Computers and Geotechnics，2014，61：144－152.

［11］CAO Y，JIANG J，HUANGW M，etal.Influence of train loading on long-term nonlinear consolidation of soil around a idealized sealing tunnel［J］.Electronic Journal of Geotechnical Engineering，2014，19（D）：929－945

［12］LIX.Stress and displacement fields around a deep circular tunnelwith partial sealing［J］.Computers and Geotechnics，1999，24（2）：125－140.

［13］DAVIS E H，RAYMOND G P.A Non-linear theory of consolidation［J］.Geotechnique，1965，15（2）：161－173.

［14］BARDON L，BERRY P L.Consolidation of normally consolidated clay［J］.Journal of the Soil Mechanics and Foundation Division，ASCE，1965，91（SM5）：15－35

［15］MESRIG，ROKHSAR A.Theory of consolidation of clays［J］.Journal of the Geotechnical Engineering Division，ASCE，1974，100（GT8）：889－903.

［16］VERRUIJTt A.A complex variable solution for a deforming circular tunnel in an elastic half-plane［J］.International Journal for Numerical and Analytical Methods in Geomechanics，1997，21（2）：77－89.

［17］詹美礼，陈绪禄.粘弹性地基中洞周土体固结问题的解析解［J］.河海大学学报（自然科学版），1993，21（2）：54－60.

［18］WONGSAROJ J.Three-dimensional finite element analysis of short-and long-term ground response to open face tunnelling in stiff clay［D］.London：Cambridge University，2005.

［19］璩继立.盾构施工引起地面长期沉降研究［D］.上海：同济大学，2002.

［20］张冬梅，黄宏伟，王箭明.软土隧道地表长期沉降的粘弹性流变与固结耦合分析［J］.岩石力学与工程学报，2003，22（Z1）：2359－2362.

［21］包鹤立.衬砌局部渗漏条件下软土盾构隧道的长期性态研究［D］.上海：同济大学，2008.

［22］程斌.车致振动下地铁隧道位移规律的研究［D］.上海：同济大学，2003.

（编辑赵丽莹）

Long-term nonlinear consolidation of soil around a shield tunnel w ith partially sealing linings under train loading

CAO Yi1，2，JIANG Jun2，XIE Kanghe2，CHENWeiyun3

（1.Hydrochina Huadong Engineering Corporation，Hydrochina Corporation，310014 Hangzhou，China；2.College of Civil Engineering and Architecture，Zhejiang University，310058 Hangzhou，China；3.Institute of Geotechnical Engineering，Nanjing Tech University，210000 Nanjing，China）

The train loading is simplified as equivalent rectangular cyclic loading in this paper to investigate the influence of train loading on long-term deformation of soft soil around a shield tunnel.Based on the empirical relation between permeability and compressibility，the governing equation of nonlinear consolidation is established.Then the analytical solutions are derived after the partially sealing lining as boundary condition is considered by introducing a dimensionless relative parameter of soil-lining permeability.The rationality of corresponding analytical solutions is confirmed by the comparison among predictions of ground settlementby presented solution and field data from Shanghai Metro Line No.1.The results show that the increment of ground settlement by train loading is positively correlated with partially sealing condition.The presented solutions provide a reasonable and effective tool for the prediction of long-term ground settlement by the operation ofmetro way.

Train loading；shield tunnel；nonlinear consolidation；analytical solution；sealing linings

TU441＋.8

A

0367－6234（2015）12－0050－07

10.11918／j.issn.0367-6234.2015.12.009

2014－05－21.

国家自然科学基金（51078329）.

曹 奕（1986—），男，博士.

蒋 军，jiangjunzju＠163.com.