纺织基小口径人工血管材料的体外水渗透性研究

方璇，薛雯，李晓才，来兴明，邓佳惠，关国平，王璐，Guidoin Robert,2

1. 东华大学纺织学院和纺织面料技术教育部重点实验室(上海，201620) 2. 加拿大拉瓦尔大学外科系

1952年， Voorhees等人应用维纶制备人工血管并移植到狗的颈动脉， 发现管壁的多孔结构对管腔内形成内膜具有积极意义[1]。此后， 人工血管的研究进入纺织材料时期。目前， 大、 中口径纺织基覆膜血管已经成功应用于临床并取得了满意的效果。然而， 小口径人工血管尚无理想的产品应用于临床， 主要是由于内皮化不完整、 远期通畅率低[2]。

为了有利于人工血管在体内实现原位内皮化， 其管壁多设计成多孔结构， 从而有利于管腔内外的物质交换。纺织材料就是理想的小口径人工血管材料， 具备规则的多孔结构、 及100%的孔连通性。然而， 管壁孔径太大会导致人工血管移植后的血液外漏， 造成不良后果。因此， 临床使用纺织基人工血管时往往需要预凝， 将血液渗透性降低到一定程度。然而， 预凝要用到病人自身血液增加了手术环节和感染风险。另一方面， 为了避免漏血， 往往将人工血管的管壁织造得很致密， 水渗透性几乎为零。这就大大削弱了纺织基人工血管的优势。

尽管已有报道研究了人工血管的孔隙率与水渗透性之间的关系[3]、 管壁均匀性[4]、 孔径大小及分布对水渗透性的影响[5]、 织物正反面水渗透性的差异[6]及渗透理论[7]等。然而， 目前尚无针对特定口径、 特定压强下纺织基小口径人工血管的水渗透性、 模拟血浆渗透性和全血渗透性方面的研究， 亦未见水渗透性与血液渗透性关系的研究。

因此， 本研究旨在探究两种机织小口径(内直径为4 mm)人工血管材料， 在不同压强下的水渗透性、 模拟血浆渗透性和抗凝全血渗透性及它们之间的相互关系。通过该量化关系， 可由体外水渗透性预测体外抗凝全血的渗透性， 为进一步研究水渗透性与体内血液渗透性之间的关系奠定基础。为临床预凝提供明确而量化的指导意见， 为开发具有适度孔隙的纺织基人工血管提供参考。

1 材料和方法

1.1 主要实验材料和仪器

30D涤纶单丝， 50D24f涤纶复丝。右旋糖酐40氯化钠注射液(四川科伦药业股份有限公司)， 人工血管整体水渗透性测试仪(自行研发)， 一次性塑料采血袋(四川南格尔生物科技有限公司)， TM3000型扫描电子显微镜(日本日立公司)。

1.2 方法

1.2.1小口径人工血管材料的制备

采用改进后的剑杆小样机一次成型内直径为4 mm的涤纶小口径人工血管管坯， 组织结构为平纹， 经纱使用30D单丝，纬纱使用50D24f复丝，设计经密为1 100根/10 cm,纬密分别为300根/10 cm，700根/10 cm。

1.2.2孔隙率计算

试样孔隙率计算参照文献已报道的方法[8]， 计算公式如式(1)：

(1)

式中：P， 孔隙率；M， 每平方米克重；t， 厚度；ρ， 涤纶密度。

1.2.3人工血管渗透性的测试方法

测试液体分别为去离子水、 模拟血浆和抗凝全血。测试试样的整体渗透性， 测试压强分别为8 kPa、 10 kPa、 12 kPa、 14 kPa、 16 kPa。在每个压强下， 测量每分钟透过人工血管材料有效长度管壁的液体量， 连续测量10 min。测试仪器采用本实验室自行研发的人工血管整体水渗透性测试仪[9]。每个压强下每种试样重复测试5次计算每个时间点的平均值， 渗透性计算公式如式(2)：

(2)

式中：W， 人工血管的液体渗透性(mL·cm-2·min-1)；Q， 一定时间内渗透过人工血管管壁的液体体积(mL)；A， 液体经过人工血管管壁的有效面积(cm2)；t， 测试时间(min)。

1.2.4扫描电子显微镜观察血细胞粘附

在抗凝全血渗透性测试之后， 抽取两种人工血管材料各5个， 每个测试压强下取1个， 共取10个。从每个材料中部剪下长14 mm、 宽4 mm的试样， 分别放入平皿中。使用多聚甲醛固定试样。将固定过的试样依次在浓度分别为60%、 70%、 80%、 90%、 95%、 100%的乙醇溶液中浸泡15 min脱水。最后， 将试样取出晾干。试样喷金后， 使用TM3000型扫描电子显微镜(SEM)观察试样内表面血细胞的粘附情况。测试电压为15 kV。每个试样阅读5个视野， 血细胞计数， 最后取平均值[10]。

1.3 数据表达及统计学分析

2 结果与讨论

2.1 人工血管材料的形态结构

试样热定型后， 实际结构参数发生变化， 与设计参数相比， 经密和纬密均有增大(表1)。这可能主要是由于热碱水溶液处理对织物有紧密化作用[11]。而且， 高温热定型对增加织物经密和纬密也有积极作用。孔隙率计算结果表明， 纬密较大的2#试样， 其孔隙率较低， 为52.4%。1#试样的孔隙率为67.6%。热定型后人工血管材料管壁结构的光学显微镜照片如图1所示。由图1可更加直观地观察到， 两种材料在孔径及其分布、 孔隙率方面存在显著差异。2#试样结构更加紧密。

表1 人工血管材料实际结构参数Tab.1 Parameters of the artificial vascular graft samples

图1 人工血管材料管壁的光学显微镜照片(×40)Fig.1 Micrographs under a light microscope of walls of vascular grafts after thermal treatment (×40)

2.2 水渗透性

由图2和图3可知， 两种试样水渗透性均随时间的延长而减小， 随着压强的增大而增大。曾有学者对水等流体在织物中的渗透进行了一系列的研究， 他们多将织物模型确定为由纤维组成的多孔介质[12]， 或内部含有许多平行于液体流动方向的毛细管的固体板材[13-14]。液态水通过试样管壁的途径主要包括：纤维表面浸润铺展及毛细传递产生的导水， 织物中的孔隙产生的透水[15]。一方面去离子水在纤维集合体表面铺展浸润的本质是液滴在固体表面铺展成膜， 原有的固-气界面消失， 而留下固-液界面和气-液界面。当固体在微观上吸附一个液体分子后， 形成固-液单分子层中的表面张力为零， 即不能再吸附液体分子。此时渗透过程的主要途径为通过织物孔隙产生透水[16]， 所以试样的水渗透性随时间的延长而减小。水及模拟血浆在管壁微孔中的流动可看作层流， 近似符合Poiseuille定律[17]， 其表达式为：

(3)

其中Q， 体积流量；R， 为管道半径；ΔP， 压差；η， 流体粘滞系数；L， 管道长度。所以当压强越大时， 去离子水的流量越大。

在8 kPa、 10 kPa、 12 kPa下， 水渗透性在测试时间内下降幅度较小， 而在14kPa、 16kPa下水渗透性下降幅度较大。这是因为在低压条件下， 试样结构相对更稳定 ， 因此水渗透性没有出现明显的下降趋势。而在高压条件下， 复丝经水流作用发生散开和重排， 管壁的平均孔径减小[11]， 固-液界面的形成加快， 因此水渗透性出现明显的下降。另外， 在各个压强下， 1#试样水渗透性均明显高于2#试样， 这说明织物孔隙率对水渗透性结果影响明显， 孔隙率越大则水渗透性越大。

图2 1#试样水渗透性结果Fig.2 Water permeability of sample 1#

图3 2#试样水渗透性结果Fig.3 Water permeability of sample 2#

2.3 模拟血浆渗透性

本文使用的模拟血浆是右旋糖酐40氯化钠注射液， 室温条件下粘滞系数为1.1 mPa·s。分析图4和图5可知， 两种试样模拟血浆渗透性均随时间的延长而减小， 随压强的增大而增大。孔隙率大的试样， 其渗透性也相对较高。同理， 在8 kPa、 10 kPa、 12 kPa下， 模拟血浆渗透性下降幅度较小， 而在14kPa、 16kPa下， 模拟血浆渗透性下降幅度较大。这些结果与水渗透性的结果相一致。结合图2和图3结果可知， 同种试样在相同压强下， 其模拟血浆渗透性小于水渗透性， 因为模拟血浆的粘滞系数大于水的粘滞系数。

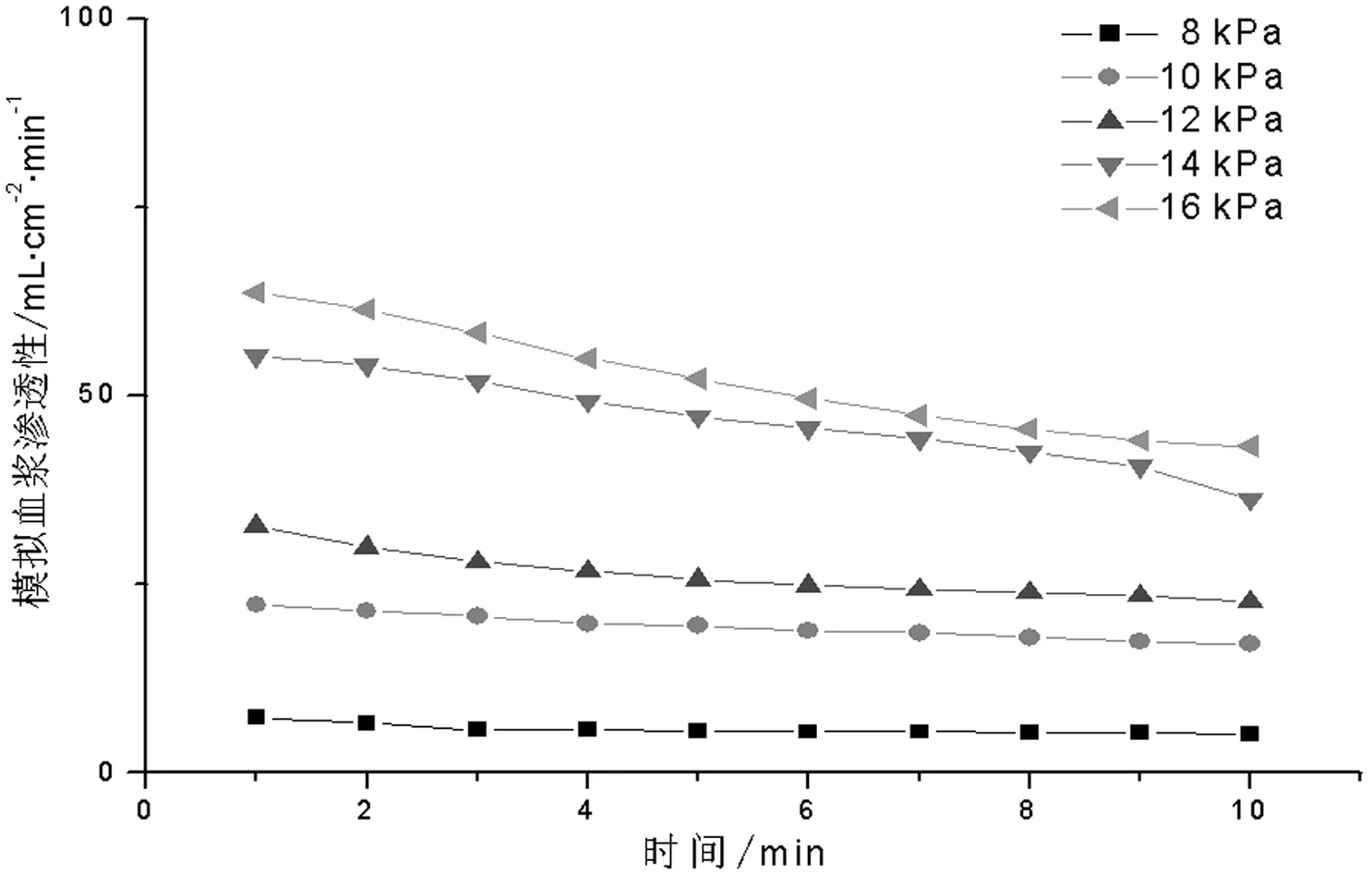
图4 1#试样模拟血浆渗透性结果Fig.4 Simulated plasma permeability of sample 1#图5 2#试样模拟血浆渗透性结果Fig.5 Simulated plasma permeability of sample 2#

2.4 水渗透性

本研究使用的抗凝全血采自健康成年猪静脉， 室温条件下粘滞系数为4.2 mPa·s。由图6和图7可知， 水渗透性随时间和压强的变化趋势与上述水渗透性及模拟血浆渗透性的变化趋势一致。然而， 两种样品的抗凝全血渗透性均远低于其水渗透性及模拟血浆渗透性。即使在16kPa条件下， 1#试样第1分钟的抗凝全血渗透性最高也只有15.11 mL·cm-2·min-1。而在8kPa条件下， 2#试样抗凝全血渗透性甚至接近0 mL·cm-2·min-1。这就说明， 液体的渗透性除了与液体的粘滞系数密切相关， 液体里面的颗粒物对渗透性也有重要影响。因为， 颗粒物的沉积或粘附会对孔径和孔隙率产生影响。由图8可知， 随着压强的增大， 试样内表面血细胞的沉积量显著增大， 孔径大的试样， 血细胞沉积数较小。

图6 1#试样抗凝全血渗透性结果Fig.6 Anticoagulant whole blood permeability of sample 1#图7 2#试样抗凝全血渗透性结果Fig.7 Anticoagulant whole blood permeability of sample 2#

图8 抗凝全血渗透性测试完成后人工血管材料内表面血细胞沉积数量Fig.8 The number of the blood cells deposited on the internal surface of artificial vascular graft after test on anticoagulant whole blood

抗凝全血在试样中的渗透过程可近似看作悬浮颗粒在多孔介质中的过滤过程。1937 年T. Iwasaki等[18]首先建立了深层过滤系统中颗粒迁移的数学模型。A. C. Payatakes 等[19]于1973年提出了颗粒状多孔介质模型， 这成为后续研究的基础。根据经典过滤模型， 悬浮颗粒沉积系数k与收集器收集效率η关系[20]可表示为式(4)：

(4)

式中：φ， 多孔介质孔隙率；u， 为悬浮颗粒速度；dc， 收集器的直径；η， 收集器收集效率。

抗凝全血在管壁毛细管渗透的过程中， 根据流体的流量连续性方程可知， 流体恒定流动中， 流过微孔某个截面的不可压缩液体的流量是相等的， 于是有：

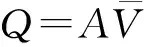
(5)

由式(5)可知， 对于同种试样而言， 在相同时间内， 透过管壁的流体的平均速度越大则流量越大。由图8可知， 当压强越高时， 抗凝全血渗透性越高。这就解释了测试压强越高、 流量越大， 血细胞沉积数量越高的现象。与1#试样相比， 2#试样表面血细胞沉积的数量更多。这是因为2#试样的孔径较小、 分布更加均匀， 截留了更多的尺寸大于孔径的颗粒， 即血细胞及其聚集体。

2.5 水渗透性与模拟血浆渗透性关系

流体介质透过多孔材料时， 在层流条件下， 同时多孔介质的直径又不至于小到能产生分子流时， 流体介质的流动特性满足线性的Darcy定律[22]：

(6)

式中q为流体流过过滤层的体积流量，k为渗透系数，AP为横截面孔隙所占的面积，ΔP为压降，μ为流体介质的动力粘滞系数，H为滤层厚度。由式(6)可知， 相同压强下， 对于同一试样而言， 有如下关系：

(7)

图9和图10分别为1#试样与2#试样水与模拟血浆渗透性之间的拟合曲线。从图9可以看出， 两种试样在各种压强下， 第1 min到第10 min的水渗透性与模拟血浆渗透性之间均存在一定的线性关系。然而， 在8 kPa条件下， 拟合曲线的相关性较低。这是因为在8 kPa条件下， 模拟血浆在管壁微孔流动过程中受固体表面对模拟血浆分子的长程范德华力作用影响较大。室温下水与模拟血浆的粘滞系数之比μ水/μ模拟血浆=0.9 mPa·s /1.1 mPa·s=0.82。而回归方程斜率在0.7～0.9之间， 即模拟血浆与水的渗透性之比在0.7～0.9之间。因此，可以认为模拟血浆渗透性与水渗透性之比近似等于水和模拟血浆的粘滞系数之比。

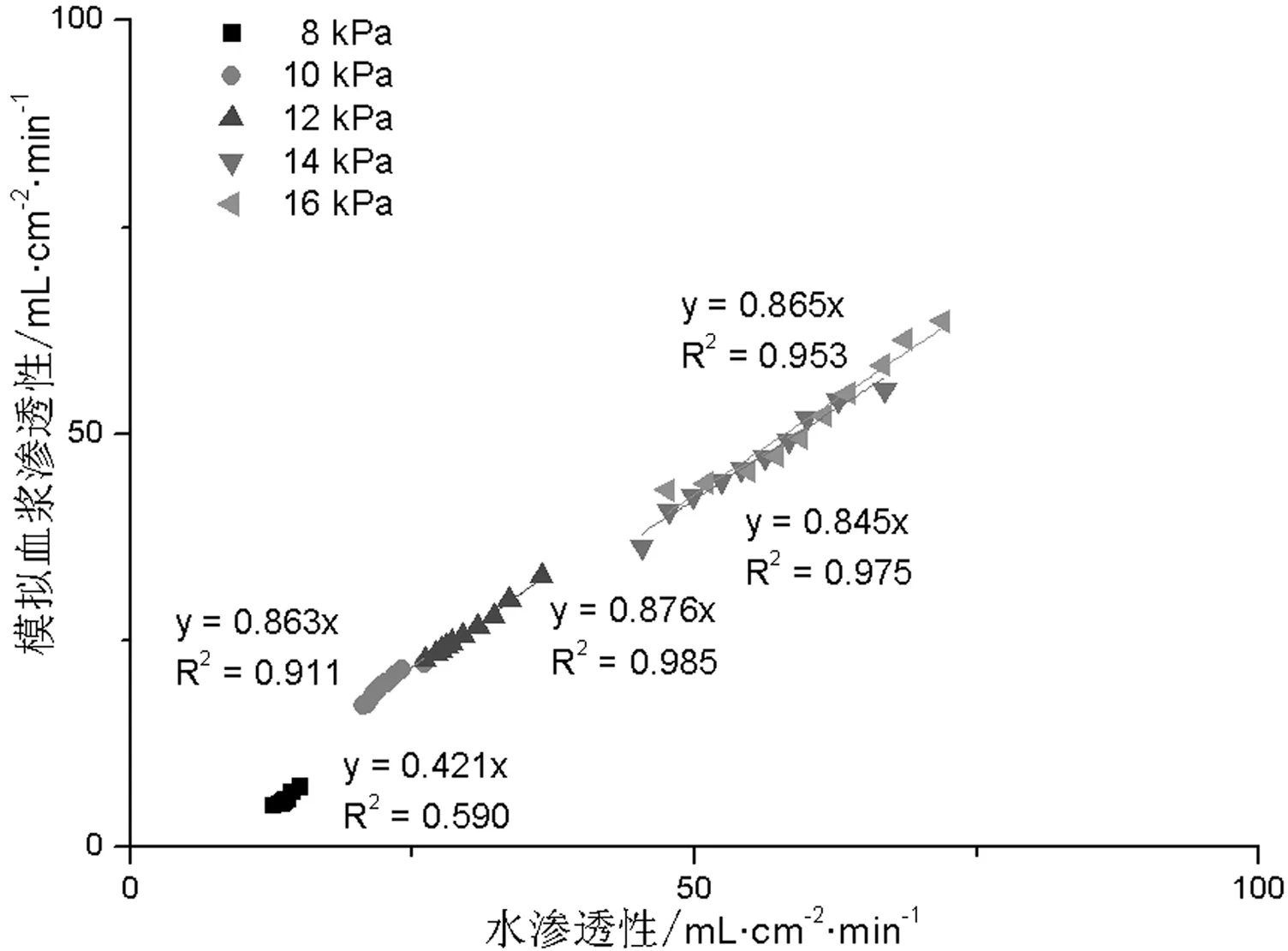
图9 1#试样水渗透性与模拟血浆渗透性关系Fig.9 Relationship between water permeability and simulated plasma permeability of sample 1#图10 2#试样水渗透性与模拟血浆渗透性关系Fig.10 Relationship between water permeability and simulated plasma permeability of sample 2#

2.6 模拟血浆渗透性与抗凝全血渗透性关系

图11和图12分别为1#试样与2#试样模拟血浆渗透性与抗凝全血渗透性之间的关系曲线。1#试样与2#试样在8 kPa、 10 kPa、 12 kPa低压下模拟血浆渗透性与抗凝全血渗透性之间存在一定的线性关系， 而在14 kPa、 16 kPa高压下呈现非线性关系。这是因为抗凝全血中存在血细胞， 血液是血细胞与血浆组成的悬浮液[23]。其粘度较大， 属于一种非牛顿流体[24]。血细胞的存在会对抗凝全血的渗透性产生显著影响。拟合曲线与Y轴交点对应的Y值， 可近似认为是当抗凝全血渗透性为0时， 即试样不渗血时模拟血浆的渗透性。

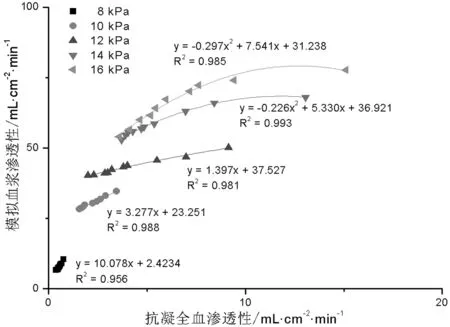
图11 1#试样抗凝全血渗透性与模拟血浆渗透性关系Fig.11 Relationship between anticoagulant whole blood permeability and simulated plasma permeability of sample 1#

图12 2#试样抗凝全血渗透性与模拟血浆渗透性关系Fig.12 Relationship between anticoagulant whole blood permeability and simulated plasma permeability of sample 2#

2.7 水渗透性与抗凝全血渗透性关系

图13和图14分别为1#试样与2#试样水渗透性与抗凝全血渗透性之间的关系曲线。1#试样在8 kPa、 10 kPa、 12 kPa下水渗透性与抗凝全血渗透性之间呈线性关系， 在14 kPa、 16 kPa高压下呈非线性相关。2#试样在8 kPa条件下抗凝全血渗透性为0， 未能得到拟合曲线。在10 kPa、 12 kPa下呈线性相关， 在14 kPa、 16 kPa下呈非线性相关。这与试样模拟血浆渗透性与抗凝全血渗透性之间有相似的关系。也就是说， 在体外由水渗透性推测抗凝全血渗透性是可行的。同时， 回归曲线与Y轴交点对应的Y值， 可认为是当抗凝全血渗透性为0时， 即当试样不渗血时的水渗透性。该值可为人工血管的结构设计提供参考， 保证人工血管在不渗血的同时， 实现最大程度的管壁内外物质交换。

3 结论

本研究通过测量不同压强下两种人工血管材料的整体水、 模拟血浆及抗凝全血渗透性， 探究了材料结构、 测试压强对渗透性的影响规律和三种渗透性之间的相互关系。得到以下主要结论：(1)水、 模拟血浆及抗凝全血渗透性均随时间的延长而减小，随测试压强的增大而增大， 随织物孔隙率增大而增大。在低压下， 渗透性下降幅度较小而在高压下降幅度较大。(2)在各个压强下， 两种人工血管材料的抗凝全血渗透性均小于模拟血浆渗透性和水渗透性。(3)模拟血浆渗透性与水渗透性之比近似等于水和模拟血浆的粘滞系数之比。(4)两种试样水渗透性与抗凝全血渗透性之间存在一定线性关系， 即通过体外实验， 由水渗透性推测抗凝全血渗透性是可行的。

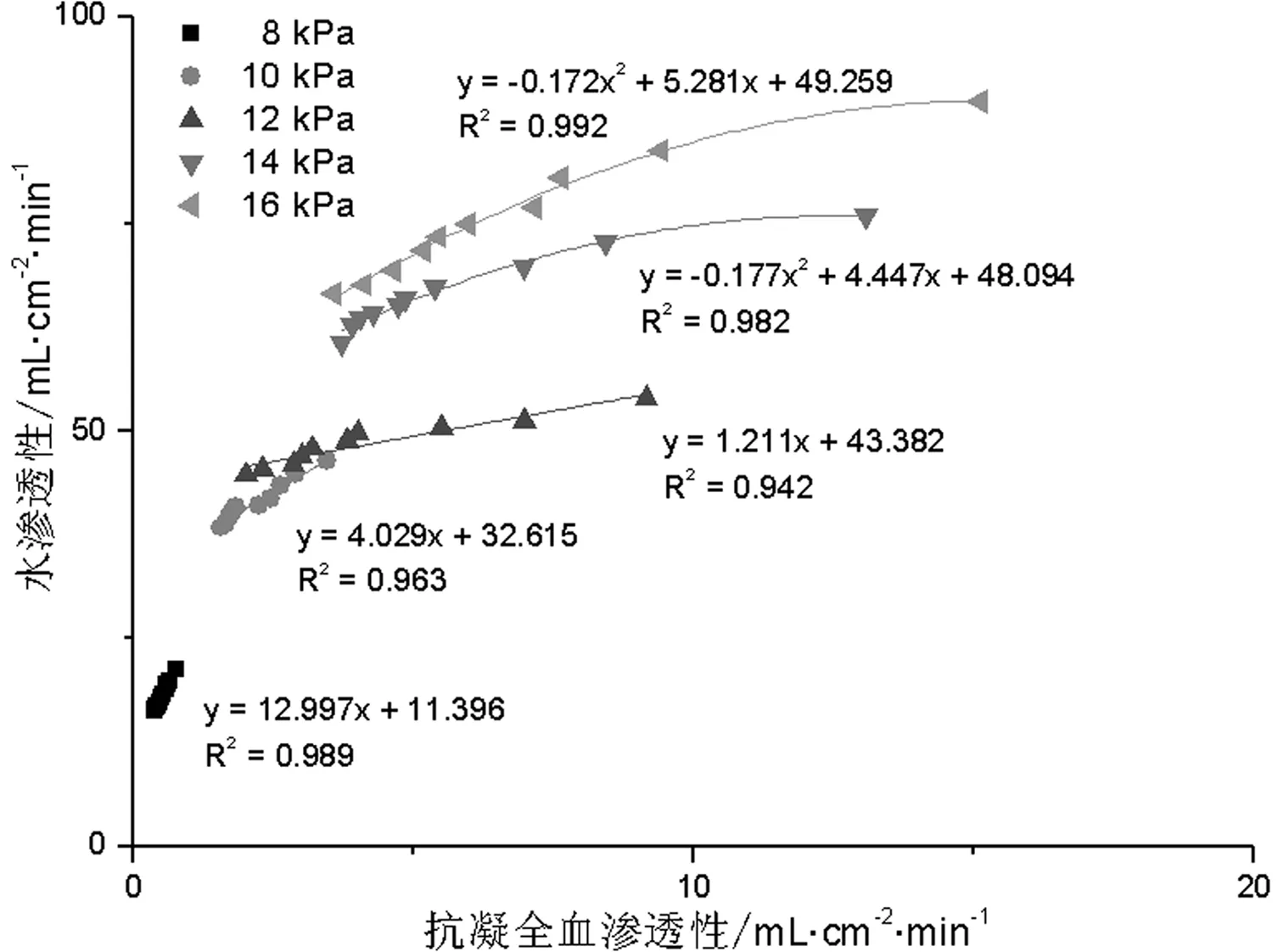
图13 1#试样抗凝全血渗透性与水渗透性关系Fig.13 Relationship between anticoagulant whole blood permeability and water permeability of sample 1#

图14 2#试样抗凝全血渗透性与水渗透性关系Fig.14 Relationship between anticoagulant whole blood permeability and water permeability of sample 2#

[1] 胡波, 何延政. 人工血管内皮化的研究进展 [J]. 中国组织工程研究, 2007, 11(10) :1923-1926.

[2] Mahara A, Somekawa S, Kobayashi N, et al. Tissue-engineered acellular small diameter long-bypass grafts with neointima-inducing activity [J]. Biomaterials, 2015, 58:54-62.

[3] Guidoin R, King M, Marceau D, et al. Textile arterial prostheses: Is water permeability equivalent to porosity? [J]. J Biomed Mater Res, 1987, 21(1):65-87.

[4] 许琭, 王璐. 两种机织型人造血管管壁的均匀特性研究 [J]. 生物医学工程学进展, 2008, 29(4) :210-214.

[5] 贾立霞,王璐,凌凯.纺织基人工血管管壁水渗透性和孔径分布研究 [J].棉纺织技术,2009,37(9):520-522.

[6] 贾立霞,刘君妹,王璐. 产业用纺织品正反面水渗透性差异的实验研究 [J]. 产业用纺织品,2010,10 :15-17.

[7] 杨夫全, 李毓陵, 陈旭炜, 等. 人工血管水渗透率的理论探究 [J]. 东华大学学报(自然科学版), 2011, 37(6) :689-692.

[8] 王璐, 丁辛, Durand Bernard. 人造血管的生物力学性能表征 [J]. 纺织学报, 2003, 24(1):7-9.

[9] 关国平, 胡星友, 沈高天, 王璐, 金伦. 压强可控的人工血管整体水渗透性测试仪及其使用方法中国CN105021510A[P].2015.

[10] 关国平. 多孔丝素蛋白材料的血管化及其组织再生性能的研究 [D]. 苏州: 苏州大学, 2009.

[11] 徐睿, 关国平, 王义斌, 等. 纺织基人工血管的水渗透性 [J]. 东华大学学报(自然科学版), 2014, 40(6) :696-700.

[12] Greenkorn R A. Porous media fluid transport and pore structure [J]. AIChE J, 1980, 26(5):876-876.

[13] Minor F W, Schwartz A M, Buckles L C, et al. The migration of liquids in textile assemblies: Part IV: Penetration of fabrics by liquids [J]. Text Res J, 1961, 31(6):525-539.

[14] Hsieh Y L. Liquid transport in fabric structures [J]. Text. Res. J, 1995, 65(5):299-307.

[15] 于伟东. 纺织材料学 [M]. 北京: 中国纺织出版社, 2006.

[16] 于伟东, 储才元. 纺织物理 [M]. 上海: 东华大学出版社, 2009.

[17] 朱克勤, 许春晓. 粘性流体力学 [M]. 北京: 高等教育出版社, 2009.

[18] Iwasaki T, Slade J J, Stanley W E. Some notes on sand filtration[with discussion] [J]. J Am Water Works Assoc, 1937, 29(10):1591-1602.

[19] Payatakes A C, Chi T, Turian R M. A new model for granular porous media: Part I. Model formulation [J]. AIChE J, 1973, 19(1):58-67.

[20] Bedrikovetsky P, Zeinijahromi A, Siqueira F D. Particle detachment under velocity alternation during suspension transport in porous media [J]. Transp Porous Media, 2012, 91(1):173-197.

[21] 国亚东. 金属橡胶液体过滤特性及试验研究 [D]. 哈尔滨: 哈尔滨工业大学, 2010.

[22] F.A.Dullien. 多孔介质: 流体渗移与孔隙结构 [M].杨富民, 等. 译.北京: 石油工业出版社, 1990.

[23] 周庆. 新型医用(血液)屏蔽织物的研究 [D]. 天津: 天津工业大学, 1999.

[24] 王鸿儒. 血液循环力学 [M]. 北京: 北京医科大学, 中国协和医科大学联合出版社, 1990.