考虑非均匀收缩徐变的PC箱梁桥时变性能

项贻强，何晓阳

（浙江大学土木工程系，310058杭州）

考虑非均匀收缩徐变的PC箱梁桥时变性能

项贻强，何晓阳

（浙江大学土木工程系，310058杭州）

为研究箱梁顶板、底板及腹板厚度差异引起的非均匀收缩徐变效应，分析了某三跨预应力混凝土（PC）连续箱梁桥时变性能.考虑混凝土抗压强度、弹性模量的时变性，分别建立模拟实际悬臂施工顺序的实体单元及梁单元有限元模型，比较成桥后在均匀及非均匀收缩徐变下的结构变形、混凝土应力和钢束应力.同时将长期挠度、钢束应力与相应规范值进行对比，并估算了车辆荷载及非均匀收缩徐变导致跨中底板出现拉应力和裂缝的时间.结果表明，与均匀收缩徐变相比，非均匀收缩徐变对跨中长期下挠影响较小，而对混凝土应力影响较大，在箱梁设计中应予以考虑.

桥梁工程；箱梁桥；悬臂施工；非均匀收缩徐变；长期下挠；混凝土应力

PC箱梁桥以其结构刚度大、变形小、行车平稳舒适等优点，被广泛应用于桥梁建设.然而，国内外PC箱梁桥下挠开裂现象日益突出，对结构的安全性和适用性构成了严重威胁，受到了工程界的普遍关注［1－3］.混凝土收缩、徐变是引起PC桥梁长期下挠的重要因素，甚至会导致桥梁倒塌［4－5］.因此，精确评估PC箱梁桥的收缩、徐变响应对控制结构下挠开裂显得尤为重要.

近年来，国内外学者从不同角度对PC箱梁的收缩徐变响应进行了各种研究.文献［6－9］采用粘弹性模型模拟混凝土徐变，分析了Koror-Babeldaob桥的长期变形，得出非均匀收缩徐变下的结构变形比均匀收缩徐变更接近实测值的结果；文献［10］编制了非均匀收缩变形分析的杆系程序，计算得到苏通刚构桥的跨中长期变形比未考虑非均匀收缩增大了5.5 cm；文献［11－13］分别基于二维湿度场和板单元研究了PC箱梁桥非均匀收缩变形，并进行了工字型试件的非均匀收缩试验；文献［14］通过粘弹性模型来模拟混凝土的徐变及预应力松弛，采用壳单元分析了箱梁桥变形，结果显示考虑非均匀收缩在长期变形分析中非常重要；文献［15－18］提出了钢筋混凝土梁开裂面的力学性能和数值模拟方法，分析了PC箱梁桥底板开裂的机理，给出了简化设计分析方法，并对混凝土箱梁桥的开裂控制方法及弯剪扭复合受力性能进行了总结.

上述研究大多采用梁壳单元分析混凝土桥梁的长期效应，无法较为精确地模拟宽箱结构的空间效应，同时较多研究仅考虑桥梁运营阶段，忽视了施工阶段对结构受力的影响.部分研究利用难以直接考虑混凝土老化的粘弹性模型来模拟徐变，导致计算有一定偏差［19］.除此之外，以上文献均仅分析了非均匀收缩徐变对结构变形的作用，几乎未关注其对混凝土应力的影响.为此本文利用CEB－FIP1990的收缩徐变模型，通过建立实体有限元模型以俘获箱梁空间受力效应，按实际悬臂施工顺序模拟，着重分析了在非均匀和均匀收缩徐变作用下，某三跨PC变截面连续箱梁桥在成桥后的变形和应力.

1 混凝土材料时变性质

混凝土材料性质会随龄期增长而变化，预测PC桥梁在施工及运营阶段的变形及应力，必须考虑混凝土材料时变性质.其主要包括抗压强度、弹性模量及收缩、徐变特性.

1.1 抗压强度

混凝土抗压强度取决于水泥类型、温度及养护条件，不同龄期混凝土的抗压强度根据下式评估［20］：

式中βcc（t）是依赖于混凝土龄期的系数.

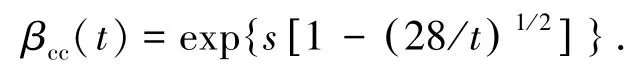
式中：fcm（t）为龄期 t时混凝土的平均抗压强度，MPa；fcm为28 d抗压强度，MPa；t为混凝土龄期，d；s根据水泥类型不同分别取0.20（快硬高强水泥）、0.25（普通及快硬水泥）及0.38（慢硬水泥）.

1.2 弹性模量

混凝土相应龄期的弹性模量可根据结构分析时划分的时间点，按下式计算［20］：

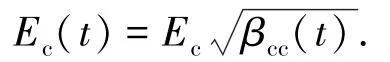
式中：Ec（t）为龄期t时混凝土的弹性模量，MPa；Ec为28 d混凝土弹性模量，MPa.

1.3 收缩

CEB－FIP规范给出了混凝土总收缩应变的计算式［20］：

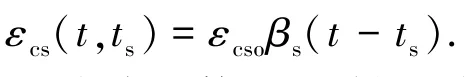
式中：εcso是名义收缩系数；βs是描述收缩系数随时间变化的函数；ts为混凝土收缩起始龄期，d.名义收缩系数可从下式得到：

式中βsc根据水泥种类不同，分别取4（慢硬水泥）、5（普通及快硬水泥）及8（快硬高强水泥）.

式中RH为环境相对湿度.函数βs的表达式为

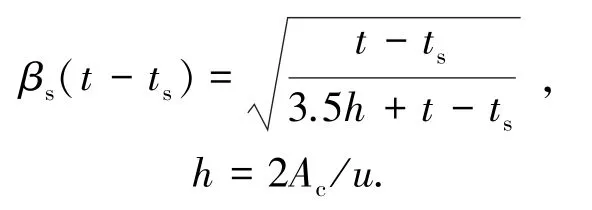
式中h是名义厚度，mm；Ac为构件截面面积，mm2；u为构件与大气接触部分的周长，mm.

1.4 徐变

混凝土的徐变系数计算如下［20］：

βc可由下式获得：

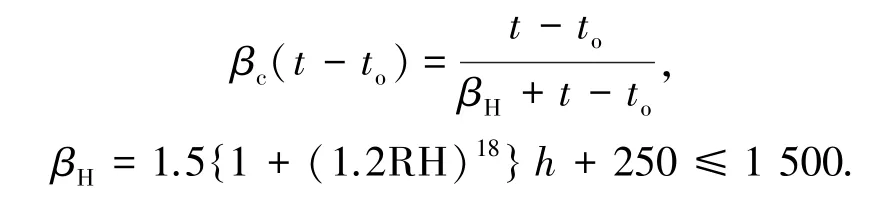
2 工程实例及计算参数

2.1 工程实例

绍兴某PC变截面连续箱梁桥立面见图1，本桥采用普通硅酸盐水泥制备的C55混凝土建造，为单向四车道设计，汽车荷载等级为公路－I级，跨径为60 m＋100 m＋60 m.全桥采用悬臂浇筑施工，箱梁截面为单箱双室截面，顶板宽19.75 m，底板宽13.5 m；根部截面梁高6 m，跨中及边跨截面梁高3 m，变截面梁段梁高按抛物线变化；顶板厚度均为30 cm，根部底板厚度为80 cm，跨中及边跨截面底板厚度为25 cm，其余按抛物线变化；腹板厚度从跨中的50 cm线性变化到墩顶处的75 cm，见图2.

图1 某PC连续箱梁桥立面布置（m）

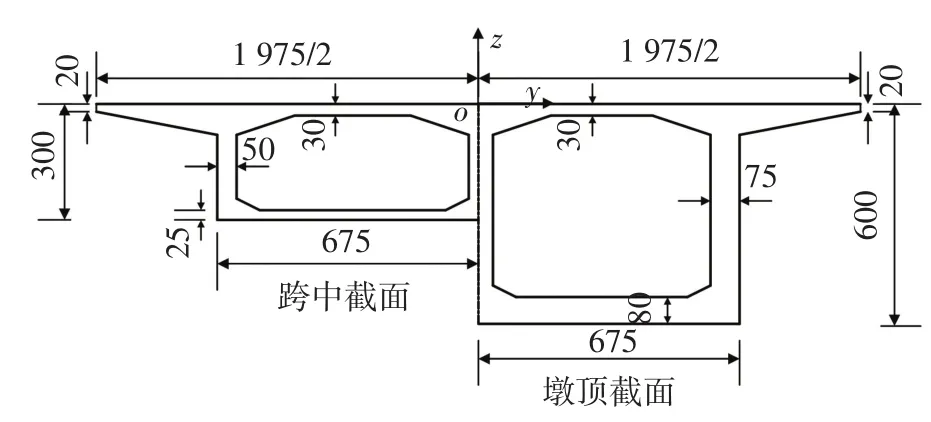
图2 某PC连续箱梁典型截面（cm）

2.2 计算参数

根据JTG D62—2004规范［21］选取材料参数，其中28 d C55混凝土弹性模量为35 500 MPa；纵横向钢束采用Φs15.2 mm预应力钢绞线，其弹性模量为195 000 MPa；竖向钢束采用Φ32 mm精轧螺纹钢筋，其弹性模量为200 000 MPa；同时取环境相对湿度为70%.

如图1所示，顶板厚度从箱梁1号到12号截面沿跨径方向基本不变，而底板和腹板厚度均连续变化，尤其是底板厚度变化较大.非均匀收缩徐变现象由各部位名义厚度h来体现，顶板名义厚度沿跨长基本不变，底板及边、中腹板沿跨径变化，且各部位名义厚度与截面平均名义厚度差异都较大.因此有必要考虑箱梁各部位不同名义厚度沿跨径变化的情况.

射波刀治疗后，口服S-1治疗2～3个疗程(剂量80 mg/m2，2次/日)，每个疗程28 d，间隔14 d。后期出现远处转移后可接受介入或静脉化疗等其他治疗手段。

3 桥梁有限元建模及荷载

3.1 计算模型

本文采用Midas Fea商用软件［22］建立了模拟施工阶段的空间有限元模型，来计算在混凝土抗压强度、弹性模量、收缩徐变等时变因素作用下，典型PC箱梁桥的非均匀收缩徐变响应.模型具有93 188个实体单元，25 196个钢筋单元.在分析中不计施工模板及铺装层对箱梁截面名义厚度的影响.

3.2 荷载

在桥梁长期响应分析中考虑以下荷载：

1）恒荷载：结构自重；

2）二期恒载：沥青铺装、管线、栏杆重量，取为3 kN／m2；

3）挂篮荷载：悬浇挂篮和模板重量按1 200 kN考虑；

4）预应力荷载：箱梁预应力钢束的初始张拉应力均为1 350 MPa，计算中扣除了由于预应力与管道壁摩擦、锚具变形等引起的瞬时损失，并在分析中分步考虑收缩徐变和预应力松弛引起的钢束应力变化；

5）汽车荷载：荷载等级为JTG D60—2004［23］规定的公路－I级，采用车道荷载加载.

3.3 施工阶段模拟

在进行混凝土结构收缩徐变分析时，是否考虑施工阶段，会造成结构分析结果有很大差异［24］.尤其对于节段施工桥梁，各节段浇筑时间不同，加载龄期不一致，且在施工期混凝土应力值变化较大，所以有必要模拟桥梁悬臂施工顺序.每个标准施工步骤包含混凝土浇筑养护、预应力张拉以及挂篮安装，持续时间为12 d.模拟标准施工步骤时，先激活混凝土节段包含的单元，同时施加该节段自重.混凝土节段强度、弹性模量、收缩徐变性质随龄期增长而变化.然后张拉该阶段钢束，并前移施工挂篮.如此反复，直到浇筑跨中合龙段时张拉主跨底板钢束.本文分析的典型PC箱梁施工节段划分及钢束布置见图3.

图3 某PC连续箱梁桥钢束布置及混凝土节段

4 计算结果及分析

4.1 结构变形

为研究各因素对结构长期下挠的影响，分别建立考虑收缩徐变的梁单元模型（模型1）、考虑均匀收缩徐变的实体单元模型（模型2）、考虑非均匀收缩徐变的实体单元模型（模型3）、考虑均匀收缩徐变且仅含纵向钢束的实体单元模型（模型4）及考虑非均匀收缩徐变且仅含纵向钢束的实体单元模型（模型5）.其中梁单元模型采用Midas Civil软件建立.梁单元与实体单元模型均使用时间增量法计算结构长期响应，区别在于后者考虑三维的收缩徐变，精度更高，并可分割箱梁各板来考虑结构的非均匀收缩、徐变问题.

图4给出了以上各模型在桥梁成桥30 a内的主跨跨中挠度.各模型成桥30 a时的跨中挠度均比运用规范［21］推荐方法得出的挠度值大，可见规范推荐方法偏于危险.与实体单元计算结果相比，梁单元分析得到的跨中挠度增长速率较慢，且两者差距随时间不断增大.在成桥30 a时，相比考虑剪力滞的实体单元模型，梁单元分析得出的下挠量小23.9%，证明箱梁的剪力滞对结构长期挠度影响较大.此外，分别比较模型2与模型4、模型3与模型5的计算值，发现时程曲线差异较小，说明横竖向钢束并不是影响跨中下挠的主要因素.

图4 不同模型下桥梁主跨跨中时变挠度

对比模型2与模型3的计算结果，发现考虑非均匀收缩、徐变的长期下挠值相对较小，该结果与文献［7、25］基本一致.这是由于底板厚度比顶板大，顶板收缩、徐变发展速率快于底板，减缓了箱梁下挠曲率增长.在成桥30 a时，两者差距为6.9%.

图5分别给出在均匀收缩、均匀徐变、非均匀收缩及非均匀徐变作用下，主跨跨中挠度的时程曲线.可见收缩和徐变对长期下挠的影响均很大，表明仅考虑非均匀收缩来预测长期变形是不精确的.同时发现，非均匀收缩引起的下挠量比均匀收缩下挠量要小.这是因为顶板厚度比底板小，水分扩散较快，顶板干燥速率大于底板，使得箱梁产生向上趋势的附加挠曲，跨中下挠量减小.

图5 均匀（非均匀）收缩（徐变）对主跨跨中挠度的影响

4.2 钢束应力

箱梁纵向预应力钢束是影响结构长期变形和应力的重要因素［4］.如图6所示，采用有限元法及规范［21］推荐方法，分析了主跨底板钢束Z1～Z3在长期荷载下的时变应力.在成桥30 a时，有限元法计算得到的钢束应力均小于规范值.在钢束张拉时，因钢束与管道壁摩擦、锚具变形，钢束应力产生瞬时损失.而后，在混凝土收缩徐变及钢筋松弛的影响下，钢束应力随时间不断减小.同时，非均匀收缩徐变作用下的钢束应力均小于均匀收缩徐变下的计算值.在成桥30 a时，两者差距达到5 MPa.相较于钢束应力，该数值较小，但数值不大的混凝土应力对此却十分敏感.

图6 主跨箱梁底板纵向钢束Z1～Z3的时变应力

4.3 混凝土应力

图7、8分别给出了主跨跨中和L／4截面顶底板纵向应力沿板宽的分布.其中t指的是所在混凝土节段的龄期.成桥后，箱梁顶底板剪力滞效应非常明显.在收缩徐变及预应力松弛影响下，跨中及L／4截面顶底板纵向压应力均随混凝土龄期增长而减小，其中底板压应力变化幅度较大，但纵向应力沿板宽的分布形状并未有显著变化.说明当桥梁成桥后，不考虑其他外荷载作用，收缩徐变效应仅改变混凝土应力值，而对纵向应力的横向分布形状无明显影响.

值得注意的是，在非均匀收缩徐变作用下，钢束应力随时间不断减小，且比均匀收缩徐变计算值小，使得结构混凝土压应力减小得更快.尤其在经过10 a非均匀收缩徐变作用后，主跨箱梁跨中底板开始出现拉应力.这对混凝土结构来说极为不利，也无法满足规范JTG D62—2004［21］对混凝土应力限值的要求.进一步选取主跨箱梁跨中底板关键点，见图9，分析其在成桥30 a内的应力变化.图10给出了主跨箱梁跨中截面典型关键点的应力时程.其中车道荷载采用主跨跨中截面最不利的四车道静力加载，并根据JTG D60—2004［23］进行横向折减，但不考虑车道荷载的徐变效应.

图7 主跨箱梁跨中截面顶底板纵向应力沿宽度的分布

图8 主跨L／4截面箱梁顶底板纵向应力沿宽度的分布

图9 主跨箱梁跨中截面典型关键点（cm）

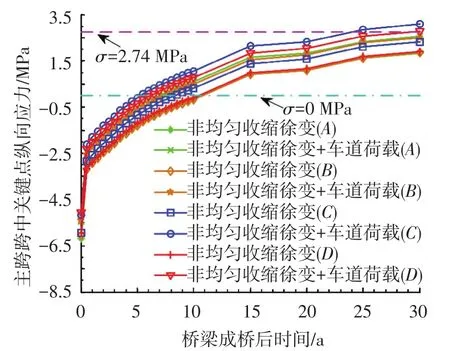
图10 主跨箱梁跨中截面典型关键点时变纵向应力

从上述分析结果可看出，主跨箱梁底板各关键点的压应力均随时间逐渐减小.若不考虑车道荷载，仅在非均匀收缩徐变作用下运营10 a左右，C点出现拉应力.若加之车道荷载，C点提前5 a出现拉应力，而其他关键点提前4 a左右出现拉应力.最为重要的是，在成桥25 a时，综合考虑非均匀收缩徐变及车道荷载的影响，C点轴向应力将超过C55混凝土的抗拉强度，引起底板开裂，进而加快桥梁的下挠.可见，PC箱梁桥非均匀收缩、徐变对桥梁混凝土应力有很大影响.为保证桥梁的安全性和适用性，在设计计算该类桥梁时，应计及该因素对混凝土长期应力的影响.

5 结 论

1）与采用实体单元计算结果相比，在成桥30 a时，采用梁单元计算的PC箱梁桥长期挠度较小，且两者均大于规范值.而仅考虑箱梁纵向钢束与考虑三向预应力作用时的长期下挠相近，说明剪力滞效应是大跨PC箱梁桥出现过大长期下挠的主要原因.

2）主跨箱梁底板钢束应力随时间不断减小，在非均匀收缩徐变作用下的应力值比均匀收缩徐变的小，且两者均小于规范值.与均匀收缩徐变相比，在非均匀收缩徐变作用下，混凝土压应力减小得较快.

3）在10 a非均匀收缩徐变作用下，主跨箱梁跨中底板开始出现拉应力.若综合考虑车辆荷载和非均匀收缩徐变效应，在成桥5 a时，跨中底板将出现拉应力，在成桥25 a时，其应力将超过混凝土抗拉强度.因此，应重视非均匀收缩徐变对混凝土应力的影响.

［1］汪剑，方志.大跨预应力混凝土箱梁桥收缩徐变效应测试与分析［J］.土木工程学报，2008，41（1）：70－81.

［2］ SOUSA H，BENTO J，FIGUEIRAS J.Construction assessment and long-term prediction of prestressed concrete bridges based on monitoring data ［J］.Engineering Structures，2013（52）：26－37.

［3］GOEL R，KUMAR R，PAUL D K.Comparative study of various creep and shrinkage prediction models for concrete［J］.Journal of Materials in Civil Engineering，2007（19）：249－260.

［4］BAZANT Z P，YU Qiang，LIGuanghua.Excessive longtime deflections of prestressed box girders.I：Record-span bridge in Palau and other paradigms［J］.Journal of Structural Engineering，2012（138）：676－686.

［5］SOUSA C，SOUSA H，NEVES A S，et al.Numerical evaluation of the long-term behavior of precast continuous bridge decks［J］.Journal of Bridge Engineering，2012（17）：89－96.

［6］KRISTEK V，BAZANT Z P，ZICH M，et al.Box girder bridge deflections：Why is the initial trend deceptive？［J］.ACIConcrete International，2006，28（1）：55－63.

［7］BAZANT Z P，YU Qiang，LIGuanghua，et al.Excessive deflections of record-span prestressed box girder：Lessons learned from the collapse of the Koror-Babeldaob Bridge in Palau［J］.ACI Concrete International，2010，32（6）：44－52.

［8］BAZANT Z P，YU Qiang，LIGuanghua.Excessive longtime deflections of prestressed box girders.II：Numerical analysis and lessons learned［J］.Journal of Structural Engineering，2012（138）：687－696.

［9］YU Qiang，BAZANT Z P，WENDNER R.Improved algorithm for efficient and realistic creep analysis of large creep-sensitive concrete structures［J］.ACI Structural Journal，2012（109）：665－675.

［10］张运涛，孟少平，刘安中.非均匀收缩对大跨径连续刚构桥长期变形的影响 ［J］.西南交通大学学报，2011， 46（3）：379－384.

［11］黄海东，向中富，郑皆连.PC箱梁桥非均匀收缩变形分析［J］.土木建筑与环境工程，2009，31（4）：60－65.

［12］向中富，谭景文，许航，等.非均匀收缩对混凝土箱梁桥挠曲变形的影响 ［J］.土木建筑与环境工程，2011，33（增刊1）：84－87.

［13］黄海东，向中富，郑皆连.混凝土结构早期非均匀收缩试验［J］.中国公路学报，2010，23（3）：64－69.

［14］MALM R，SUNDQUIST H.Time-dependent analyses of segmentally constructed balanced cantilever bridges［J］.Engineering Structures，2010（32）：1038－1045.

［15］唐国斌，项贻强.钢筋混凝土梁开裂面的力学性能和数值模拟［J］.水利学报，2015，46（1）：42－50.

［16］XIANG Yiqiang，TANG Guobin，LIU Chengxi.Cracking mechanism and simplified design method for bottom flange in prestressed concrete box girder bridge［J］.Journal of Bridge Engineering，2011，16（2）：267－274.

［17］项贻强，唐国斌.混凝土箱梁桥开裂机理及控制 ［M］.北京：中国水利水电出版社，2010.

［18］项贻强，程坤，吴强强.钢筋混凝土构件弯剪扭复合受力分析研究与进展［J］.中国公路学报，2014，27（4）：46－54.

［19］黄海东，向中富，郑皆连.PC箱梁桥三维徐变效应精细化分析［J］.中国公路学报，2013，26（5）：108－114.

［20］CEB-FIP MC90.CEB-FIP model code for concrete structures［S］.London：T Telford，1993.

［21］中华人民共和国交通部.JTG D62—2004公路钢筋混凝土及预应力混凝土桥涵设计规范［S］.北京：人民交通出版社，2004.

［22］北京迈达斯技术有限公司.MIDAS／FEA分析与计算原理［M］.北京：北京迈达斯技术有限公司，2008.

［23］中华人民共和国交通部.JTG D60—2004公路桥涵设计通用规范［S］.北京：人民交通出版社，2004.

［24］ATES S.Numerical modelling of continuous concrete box girder bridges considering construction stages［J］.Applied mathematicalmodelling，2011（35）：3809－3820.

［25］TAKACSP F.Deformation in concrete cantilever bridges：Observations and theoretical modelling［D］.Trondheim：Norwegian University of Science and Technology，2002.

（编辑赵丽莹）

Time-dependent behavior of PC box girder bridges considering non-uniform shrinkage and creep

XIANG Yiqiang，HE Xiaoyang

（Department of Civil Engineering，Zhejiang University，310058 Hangzhou，China）

The time-dependent behavior of a typical three-span prestressed concrete（PC）continuous box girder bridge was analyzed to investigate the effect of non-uniform shrinkage and creep due to thickness differences among webs and top and bottom flanges in box girders.Considering time-varying effects of compressive strength and elasticitymodulus of concrete，finite elementmodels which simulated cantilever-construction by solid and beam elementswere developed，respectively.A comparative study on structural displacement，concrete stress and tendon stress caused by uniform and non-uniform creep and shrinkage after bridge completion was peformed.Meanwhile，long-term deflection and tendon stress were compared with relevant values which were calculated according to the standard.And the time when tensile stress and crack resulting from vehicle load and non-uniform creep and shrinkage in the bottom flange appeared was estimated.The results show that compared with uniform creep and shrinkage，non-uniform creep and shrinkage have smaller influence on the long-term deflection atmidspan，and have greater effect on the concrete stress，which should be concerned in design of box girders.

bridge engineering；box girder bridge；cantilever construction；non-uniform shrinkage and creep；longterm deflection；concrete stress

U448

A

0367－6234（2015）12－0117－06

10.11918／j.issn.0367-6234.2015.12.021

2014－11－30.

国家自然科学基金（51178416）.

项贻强（1959—），男，教授，博士生导师.

何晓阳，hxysunrise＠zju.edu.cn.