新型灌浆套筒的约束机理及约束应力分布

郑永峰，郭正兴，曹 江

（东南大学土木工程学院，210096南京）

新型灌浆套筒的约束机理及约束应力分布

郑永峰，郭正兴，曹 江

（东南大学土木工程学院，210096南京）

为降低预制装配混凝土结构中的钢筋连接成本，利用无缝钢管，采用冷滚压工艺研制了一种新型钢筋连接用灌浆套筒，通过接头单向拉伸试验，主要研究了套筒的约束机理及约束应力分布.结果表明：该新型接头能够满足JGJ107—2010规定的单向拉伸强度要求；套筒在灌浆料硬化阶段产生的初始约束应力与钢筋、灌浆料、套筒的力学特性及接头尺寸有关，并随灌浆料膨胀率的增加呈线性增长；套筒变形段对灌浆料的平均约束应力大于套筒光滑段，变形段约束主要来自内壁环肋处相互挤压力的径向分力，光滑段对灌浆料的约束取决于灌浆料劈裂变形的大小.

预制混凝土结构；灌浆套筒；接头；约束机理；约束应力分布

钢筋套筒灌浆连接是在预制混凝土构件内预埋的金属套筒中插入钢筋并灌注水泥基灌浆料而实现的钢筋连接方式.该方式于上世纪60年代末由Alfred A.Yee首次提出，随后在北美、日本、欧洲等地得到了广泛的工程应用［1］.由于目前国内外套筒产品均为球磨铸铁铸造或采用优质碳素结构钢数控车床加工而成，套筒制作成本较高，造成中国市场上灌浆套筒的价格远高于现浇结构中采用的螺纹套筒，预制构件的连接问题成为制约中国预制装配混凝土结构发展的关键问题之一.

钢筋套筒灌浆连接的承载力取决于钢筋、灌浆料及套筒三者间的相互黏结强度.研究表明，通过限制混凝土或灌浆料的劈裂变形，可有效提高钢筋的黏结强度［2－3］.钢筋套筒灌浆连接正是基于这一原理，通过套筒对填充灌浆料的约束，提高钢筋黏结强度，减小钢筋锚固长度.因此，合理预测套筒对灌浆料的约束作用成为计算钢筋套筒灌浆连接承载力的关键.

本文针对灌浆套筒在应用中存在的问题，提出了一种新型灌浆套筒－GDPS（grouted deformed pipe splice）套筒［4］，该套筒在加工工艺、外形及内腔构造方面与现有套筒产品有显著差异，通过单向拉伸试验及理论分析，对该套筒连接的性能及约束机理进行研究.

1 试 验

GDPS套筒采用Q390B无缝钢管加工而成，钢管材性见表1.套筒两端内壁和外壁分别设置了多道弧形凸环肋及环状倒梯形凹槽，环肋和凹槽通过冷滚压一次成型.连接钢筋采用HRB400钢筋，材性见表2.灌浆料水胶比为0.27，水养条件下的体积变形率见图1.根据与接头试件同时浇筑同条件养护的试块（40 mm×40 mm×160 mm）测定的灌浆料抗压强度为70.2 MPa，抗折强度14.0 MPa.

接头试件尺寸见图2，主要参数见表3.套筒外径及壁厚按以下原则确定：套筒锚固段环形凸起部分的内径最小尺寸与钢筋公称直径的差值≥10 mm［5］.同时，按《钢筋机械连接技术规程》［6］规定（I级接头抗拉强度≥1.1倍钢筋抗拉强度标准值），套筒截面尺寸偏安全应满足fsyk×As≥1.1×fstk×Ab要求.式中fsyk为钢管屈服强度标准值，As为套筒中部截面面积，fstk为钢筋抗拉强度标准值，Ab为钢筋公称截面面积.

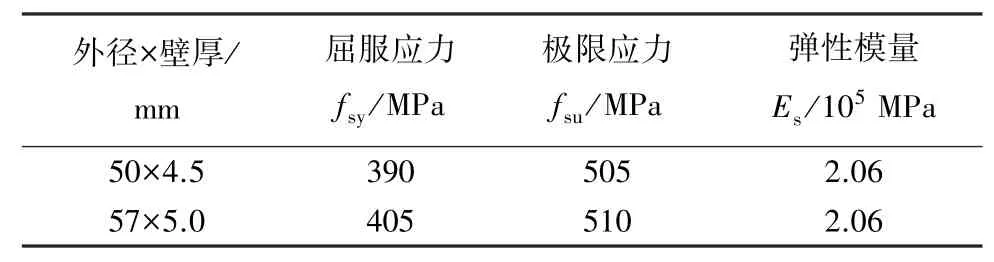
表1 套筒加工用无缝钢管材料性能

表2 连接钢筋材料性能

试件浇筑后置于标准养护室内养护38 d后在万能试验机上进行拉伸试验，见图3.为研究GDPS灌浆套筒接头的约束机理，在套筒外表面密集粘贴了轴向及环向应变片，在连接钢筋表面粘贴了轴向应变片.

图1 灌浆料体积变形率

图2 试件尺寸（mm）

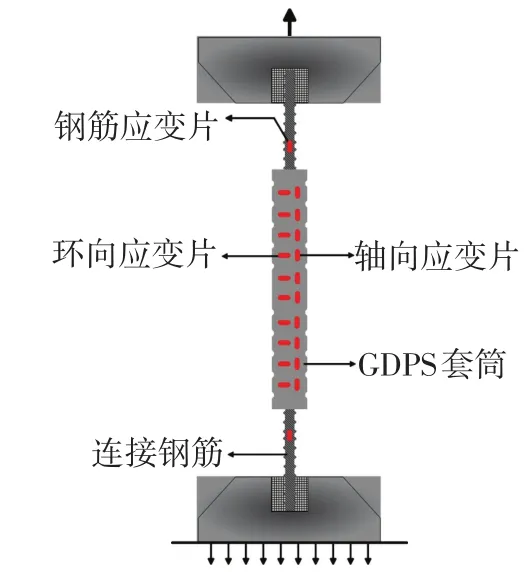
图3 试验加载装置

2 主要结果

2.1 结构性能关键指标及破坏形态

主要试验结果见表3.试件抗拉强度与连接钢筋抗拉强度标准值的比值fu／fbuk均不小于1.10，符合JGJ107—2010［6］中的Ⅰ级接头单向拉伸强度要求，表现出良好的结构性能.试件SM－D22－2和SM－D25－2之所以出现拔出破坏，主要是由于钢筋超强造成.

表3 试件参数及主要试验结果 mm

试件出现了钢筋断裂（图4）和钢筋拔出（图5）两种破坏模式.为观察套筒内部灌浆料的破坏形态，试件破坏后将其对称剖开，见图6、7.图6为钢筋断裂破坏试件SM－D25－1剖开后的破坏状况，套筒端部灌浆料在钢筋断裂时呈锥形剥落，灌浆料在套筒中线及中部第一道肋处呈环形开裂，同时在套筒变形段存在多道劈裂斜裂缝，钢筋横肋、灌浆料及套筒环肋之间的相互作用造成斜裂缝从钢筋横肋指向套筒内壁环肋，最大裂缝宽度约0.1mm.在套筒变形段可见钢筋从套筒端部逐肋向内部发生了黏结滑移，钢筋横肋背面与灌浆料拉脱（间隙逐肋向内减小），肋前灌浆料被局部压碎，最外侧四道钢筋横肋间的灌浆料已被剪断；在钢筋锚固段的后半部分，钢筋与灌浆料间未见明显拉脱，灌浆料压碎现象.套筒与灌浆料之间粘结良好，全长均未发现明显拉脱及灌浆料压碎现象，表明黏结强度仍有较大富裕.

图7为钢筋拔出破坏试件SM－D25－2剖开后的破坏状况，与钢筋断裂破坏试件相比主要差异在于：一端连接钢筋由于钢筋横肋之间的灌浆料咬合齿全部被剪断而产生明显滑移，随着持续加载及滑移发展，滑移面不断地被磨损、挫平，最终形成光滑滑移面.另一端钢筋在锚固段内均可见钢筋横肋背面与灌浆料拉脱现象（间隙逐肋向内减小），肋前灌浆料被局部压碎，除钢筋锚固段尾部4道横肋与灌浆料的咬合齿未被剪断外，其余咬合齿均已发生剪切破坏.

图4 钢筋断裂破坏

图5 钢筋拔出破坏

图6 试件SM－D25－1剖切图

图7 试件SM－D25－2剖切图

2.3 套筒应变特点及分布规律

图8为SM－D22系列试件套筒轴向应变沿套筒长度的分布曲线，为减小由于灌浆料非匀质性及套筒凸环肋处应力集中造成的试验结果离散，应变值取同系列3个试件应变的平均值.曲线可分3段，左、右段为套筒变形段的应变，中部为光滑段的应变，以套筒中线近似呈对称分布.套筒光滑段轴向应变从套筒中线向两端衰减，并在中部第一道肋处从拉应变突变为压应变.套筒变形段轴向应变为压应变，峰值位于中部第一道肋外侧，并向套筒端部衰减.其余试件表现出与SM－D22－1类似的规律，限于篇幅未一一列出.

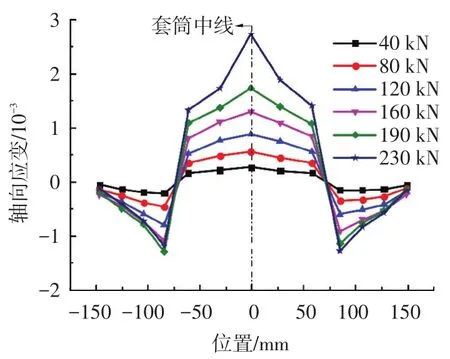
图8 套筒轴向应变分布规律

表4为SM－D22及SM－D25系列试件套筒光滑段和变形段与灌浆料的平均黏结应力计算结果.τs，1为套筒光滑段与灌浆料平均黏结应力，近似按式（1）计算：

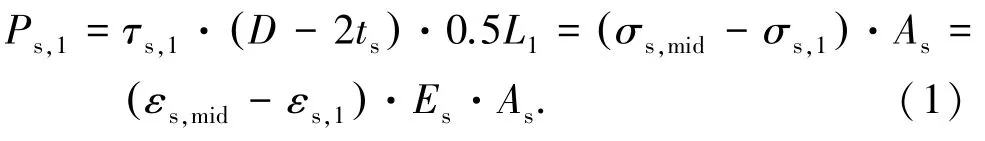
式中：εs，1为套筒光滑段端部的轴向应变；εs，mid为套筒中部轴向应变；As为套筒截面面积；τs，2为套筒变形段与灌浆料平均黏结应力，按式（2）计算；τs为套筒全长与灌浆料的平均黏结应力，按式（3）计算.

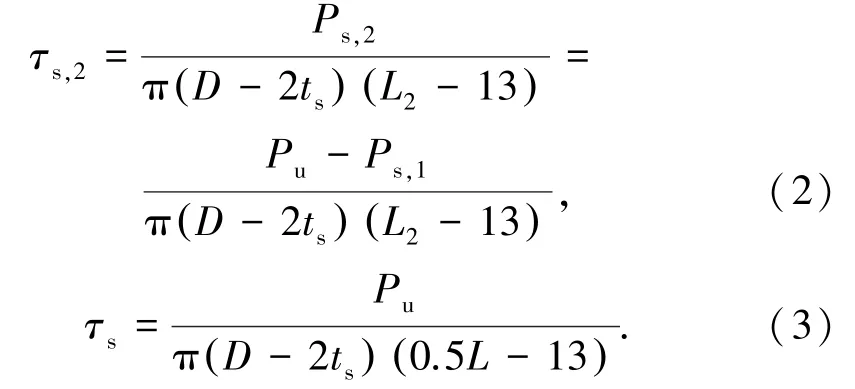
根据计算结果，套筒光滑段的平均黏结应力仅略小于变形段，黏结力Ps，1约为试件破坏荷载Pu的40%，可以推断套筒变形段与灌浆料的机械咬合力尚未达到峰值，黏结强度仍有较大富裕.这一结果与图6所观察到的破坏形态吻合，试件破坏时套筒环肋与灌浆料之间未见明显的拉脱及灌浆料压碎现象.

表4 套筒－灌浆料平均黏结应力

图9为SM－D22系列试件套筒环向应变沿套筒长度方向的分布曲线，为减小试验结果的离散，应变值取同系列3个试件应变的平均值.该曲线与荷载－轴向应变关系曲线类似，可分3段，左、右段为套筒变形段的应变分布，中部为套筒光滑段的应变分布.曲线存在3个峰值点，分别位于套筒中部和中部两侧第一道肋外侧.光滑段环向应变从套筒中线处向两端衰减，变形段从中部第一道肋处向套筒端部衰减.

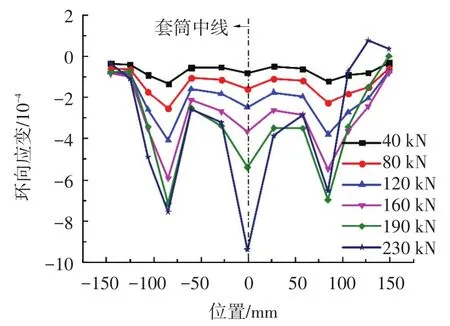
图9 套筒环向应变分布规律

3 约束应力分布

3.1 灌浆料硬化阶段初始约束应力

灌浆料浇筑后，由于其膨胀变形受到套筒的约束，将在灌浆料内产生预压应力，在套筒内产生预拉应力，在钢筋－灌浆料－套筒界面上产生约束压力.该约束将延缓灌浆料的劈裂并对灌浆料劈裂前的钢筋黏结性能有重要影响.

若假定灌浆料在硬化膨胀过程中处于弹性状态，由于钢筋套筒灌浆连接在灌浆料硬化阶段仅受到灌浆料膨胀变形产生的径向作用，并且轴向尺寸远大于径向尺寸，轴向差异对计算结果的影响较小，可简化为平面应变问题，众多学者［2，7－8］通过理论及试验对该简化的可行性进行了验证.同时，灌浆套筒连接在灌浆料硬化阶段属于轴对称问题，剪应力为0.根据厚壁圆筒模型［9］，筒壁任一点的径向应力σr和环向应力σθ为：

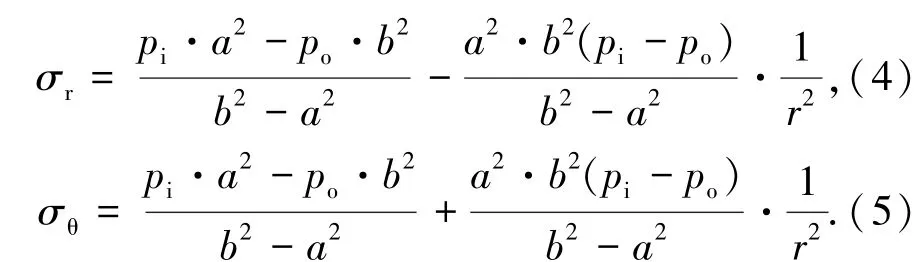
式中：a为筒壁内径，b为筒壁外径，pi为筒壁内表面压力，po为筒壁外表面压力.灌浆套筒连接接头的受力模型见图10.

对于灌浆套筒，在r＝rs处的径向应力、环向应力及径向位移分别为：

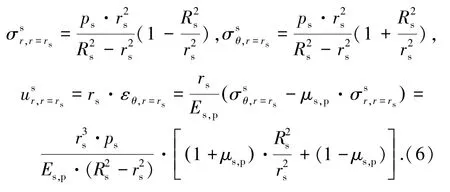
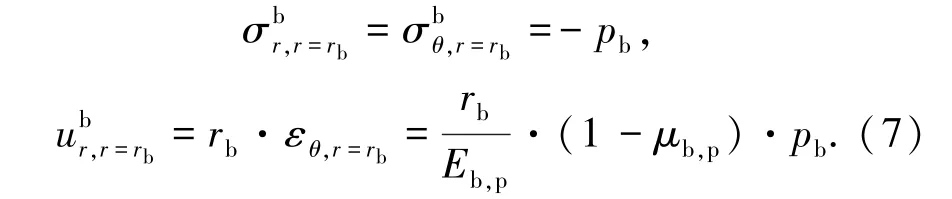
对于灌浆料，考虑浆体在硬化过程中的膨胀变形［8］，在r＝rb处的径向应力及径向位移分别为：

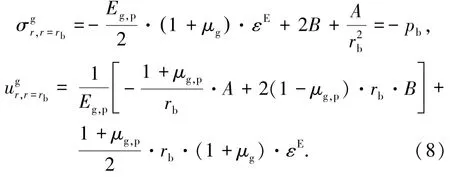
在r＝rs处的径向应力及径向位移为：

式中：A，B为待定常数，上标b表示钢筋，g表示灌浆料，s表示套筒.

图10 钢筋套筒灌浆连接受力模型

在钢筋与灌浆料及灌浆料与套筒接触面上有边界条件：接触面上的径向位移相等，即

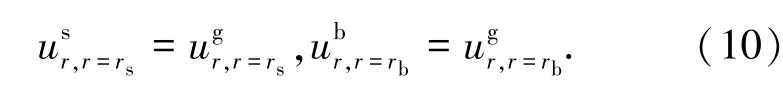
联立式（6）～（10）可得钢筋与灌浆料及灌浆料与套筒接触面上的界面压力pb和ps：

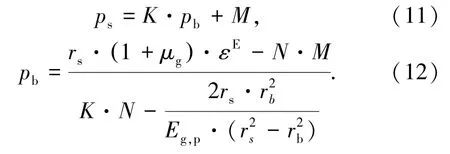
式中：

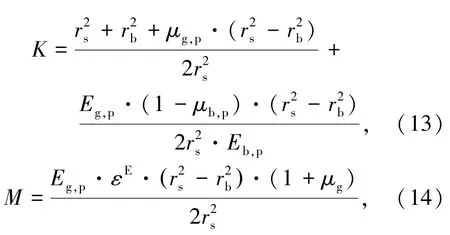
从式（11）～（15）可知，界面处的约束压力与套筒、灌浆料、钢筋的力学特性及钢筋、套筒尺寸有关，当以上指标确定后，K、M、N为常数，界面压力与灌浆料的膨胀率呈正比.

本文采用的材料力学特性如下：套筒平面应变换算弹性模量Es，p＝226.4 GPa，钢筋平面应变换算弹性模量Eb，p＝219.8 GPa，套筒和钢筋的平面应变换算泊松μs，p＝μb，p＝0.429，灌浆料泊松比μg＝0.2，平面应变换算泊松比μg，p＝0.25，灌浆料的弹性模量取钢管弹性模量的1／18［10］，即11.4 GPa，平面应变换算弹性模量Eg，p＝11.9 GPa.需要注意的是，由于灌浆料早期塑性膨胀阶段的弹性模量很小，因此忽略该阶段产生的约束应力，灌浆料自由膨胀率εE近似取试验时的膨胀率与浇筑1 d后的膨胀率的差值，即

初始约束应力（界面压力）及灌浆料最大膨胀率计算结果见表5.套筒与灌浆料之间的界面压力大于钢筋与灌浆料之间的界面压力，若不考虑两个接触面上摩擦系数的差异，由于灌浆料与套筒间的摩擦面积远大于与钢筋的摩擦面积，灌浆料与套筒之间的摩擦力远大于与钢筋之间的摩擦力.

表5 界面初始约束应力及摩擦力

3.2 钢筋黏结破坏时的约束应力

在拉力作用下，由于钢筋的“锥楔”作用，灌浆料产生径向位移，在套筒的约束下，浆体硬化过程中产生的初始约束增大，环向预压应力σgθ减小.随着荷载增加，σgθ逐渐转变为拉应力，当应力超过灌浆料的抗拉强度时，即在钢筋－灌浆料界面处出现劈裂裂缝.裂缝出现后，未开裂区域发生应力重分布，厚璧圆筒模型的基本假定不再成立，灌浆料传力路径发生转变.当灌浆料完全劈裂后，钢筋－灌浆料界面压力通过被裂缝分割的灌浆料小柱传递到套筒－灌浆料界面.

3.2.1 套筒变形段约束应力

试验结果表明，套筒变形段环肋间筒壁轴向及环向应变均为压应变，这主要是由于变形段凸环肋与灌浆料的相互作用造成，见图11.在凸环肋处，环肋与灌浆料之间挤压力的轴向分力阻止灌浆料跟随钢筋滑移，径向分力则约束灌浆料的劈裂膨胀变形.从试件剖开后的破坏形态可见，灌浆料在套筒变形段存在明显的劈裂膨胀，而套筒环肋间的环向应变却始终为压应变，表明环肋处挤压力的径向分力对灌浆料的约束作用非常明显.因此，本文对套筒变形段的约束仅考虑该径向分力，忽略环肋间筒壁对灌浆料的径向约束.

图11 灌浆料与套筒变形段相互作用

根据套筒内腔结构，套筒与灌浆料的黏结承载力可分为光滑段和变形段两部分，光滑段和变形段的黏结力Ps，1和Ps，2分别为

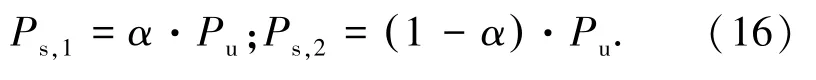
α由试验结果确定（表4），试件破坏时，套筒变形段的黏结力Ps，2主要为摩擦力Ps，f和机械咬合力Ps，zi，则

式中Ps，zi和Ps，ri分别为套筒变形段凸环肋上挤压力的轴向分力和径向分力，ki为两者的比值.从试件破坏后的剖切图可见，灌浆料与套筒之间黏结良好，未见灌浆料压碎现象.因此，假定钢筋拔出破坏时，套筒环肋周边灌浆料处于弹性状态，未出现受压破坏，则各环肋处的ki相等，并可由环肋形状确定.ps，2r为凸环肋处径向分力产生的平均约束应力，n为套筒一端变形段的凸环肋的数量，hr为内壁凸环肋净高，为2.5 mm，μ为摩擦系数［11］.

联立式（17）和（18）可推出

联立式（17）和（19）可推出

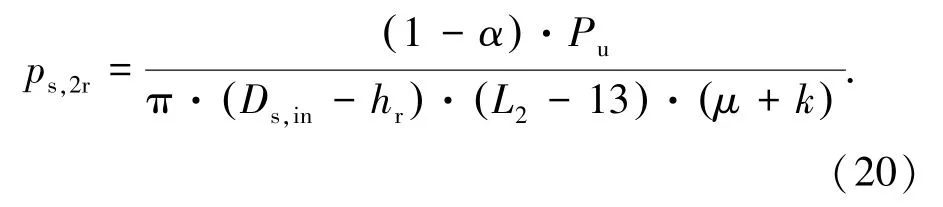
从图5可见，试件破坏时纵向劈裂裂缝已延伸至变形段末端，因此钢筋－灌浆料界面压力pb，2r已全部传递到套筒－灌浆料界面［2］.

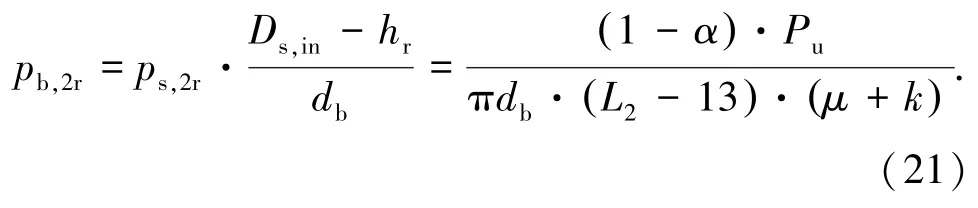
根据上述公式，黏结破坏试件SM－D22－2和SM－D25－2在套筒－灌浆料界面处的约束应力分别为11.65 MPa和13.01 MPa，在钢筋－灌浆料界面处的约束应力分别为20.38 MPa和23.14 MPa.

3.2.2 套筒光滑段约束应力

对于套筒光滑段，其对灌浆料的约束应力可根据试验结果按式（22）［12］计算：

式中：Esθ为套筒环向弹性模量，νsθ为套筒环向泊松比，νsz为套筒轴向泊松比，εsθ为套筒环向应变，εsz为套筒轴向应变.本文假定套筒为各向同性材料，则Esθ＝206 GPa，νsθ＝νsz＝0.3，εsθ和εsz按实测值.计算结果如图12所示：套筒光滑段约束应力呈“M”型，中部约束应力最小，向两端逐渐增大，到达峰值后再逐渐减小；试件SM－D25－2光滑段平均约束应力为4.23 MPa，试件SM－D22－2为6.64 MPa；由于试件SM－D22－2在黏结破坏时，套筒中部已屈服，该点的约束应力计算值失真，计算平均值时未考虑该点，因此其实际平均约束应力应小于6.64 MPa.

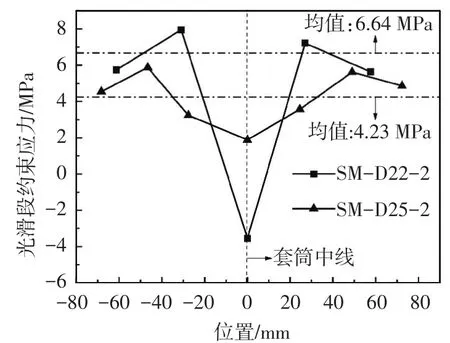
图12 套筒光滑段约束应力

套筒光滑段的约束应力小于变形段，试件SMD22－2和SM－D25－2光滑段约束应力值分别为变形段的57.0%（实际值更小）和32.5%.表明变形段灌浆料产生了更大的膨胀变形，与破坏状况一致.

4 结 论

1）本文GDPS套筒接头试件的钢筋锚固长度为6.9～7.5倍钢筋公称直径，接头抗拉强度与钢筋抗拉强度标准值的比值均不小于1.10，满足规范对接头的单向拉伸强度要求.

2）灌浆料硬化阶段产生的套筒初始约束与接头材料力学特性及尺寸有关，并随灌浆料膨胀率的增加呈线性增长；套筒－灌浆料间的初始界面压力大于钢筋－灌浆料界面压力.

3）荷载作用下，套筒光滑段对灌浆料的约束作用小于变形段，黏结破坏试件SM－D25－2光滑段约束应力值为变形段的32.5%，SM－D22－2光滑段约束应力值小于变形段的57.0%.

4）对于HRB400钢筋，灌浆套筒可按以下原则设计：套筒截面宜满足fsyk×As≥1.1×fstk×Ab；套筒长度L≥2La＋密封塞厚度＋钢筋安装调整长度，钢筋锚固长度La可取7.5 d.

［1］LING J H，ABD RAHMAN A B，IBRAHIM I S，et al.Behaviour of grouted pipe splice under incremental tensile load［J］.Construction and Building Materials，2012，33：90－98.

［2］MALVAR L J.Bond of reinforcement under controlled confinement［J］.ACIMaterials Journal，1992，89（6）：593－601.

［3］MOOSAVIM，JAFARI A，KHOSRAVI A.Bond of cement grouted reinforcing bars under constant radial pressure［J］.Cement and Concrete Composites，2005，27（1）：103－109.

［4］郭正兴，郑永峰，刘家彬，等.一种钢筋浆锚对接连接的灌浆变形钢管套筒：ZL201320407071.4［P］.2014－01－15.

［5］JG／T 398—2012钢筋连接用灌浆套筒［S］.北京：中国标准出版社，2012.

［6］JGJ107—2010钢筋机械连接技术规程［S］.北京：中国建筑工艺出版社，2010.

［7］YAZICIS，KAISER P K.Bond strength of grouted cable bolts［C］／／International Journal of Rock Mechanics and Mining Sciences＆ Geomechanics Abstracts.Pergamon：［s.n.］，1992，29（3）：279－292.

［8］蒋首超，王震.预应力灌浆套管中初始应力分布理论分析［J］.工程力学，2012，30（4）：301－309.

［9］徐芝纶.弹性力学［M］.北京：高等教育出版社，2006.

［10］Health＆ Security Executives.Pile／sleeve connections［R］.Norwich：Offshore Technology Report，2002.

［11］RABBAT BG，RUSSELL H G.Friction coefficientof steel on concrete or grout［J］.Journal of Structural Engineering，1985，111（3）：505－515.

［12］KIM H K.Bond Strength ofmortar-filled steel pipe splices reflecting confining effect［J］.Journal of Asian Architecture and Building Engineering，2012，11（1）：125－132.

（编辑赵丽莹）

Confinementmechanism and confining stress distribution of new grouting coup ler for rebars splicing

ZHENG Yongfeng，GUO Zhengxing，CAO Jiang

（School of Civil Engineering，Southeast University，210096 Nanjing，China）

The novel grouting coupler was developed using seamless steel pipe through cold rolling press to reduce the cost of rebars splicing used in precast connection.Based on incremental tension test，the confinement mechanism and distribution of confining stress in the sleeve were studied.It is shown that the ultimate strength of this new splice can meet the regulation specified in JGJ107—2010.The initial confining stresses caused during the hardening process of the infilled grout are related to themechanical properties of the spliced bars，grout and sleeve and dimensions of the splice.When these parameters are determined，the confining stress increased linearly with the increment of free expansion rate of the grout.The average confining stress in the deformed part is greater than it in the smooth part.For the deformed part，the confinement is mainly provided by the radial component of the interaction between the concentric ribs and the infilled grout.On the other hand，the confining stress in the smooth part is controlled by the dilation of the inner grout.

precast concrete structure；grouting coupler；splice；confinementmechanism；distribution of confining stress

TU39.04

A

0367－6234（2015）12－0106－06

10.11918／j.issn.0367-6234.2015.12.019

2014－12－03.

国家科技支撑计划项目（2011BAJ10B03）.

郑永峰（1981—），男，博士研究生；郭正兴（1956—），男，教授，博士生导师.

郭正兴，guozx195608＠126.com.