基于滑模变结构控制的Buck变换器研究

李美芳，尹 军2

（1.山西大学电力工程系，山西太原030013；2.山西太钢不锈钢股份有限公司，山西 太原030003）

0 引 言

近年来，在电力电子变换器领域，为进一步提高变换器性能，各种先进控制策略以其优良的特性得到广泛的研究。滑模变结构控制［1，2］简称滑模控制（Sliding Mode Control，SMC）是变结构控制的一种有效控制方法，对电力电子开关变换器非线性特质具有天然的适用性，采用滑模变结构控制的变换器具有稳定范围宽、动态响应快、鲁棒性强、控制实现简单等优点，成为研究的热点。

文献［3，4］以Buck变换器为例，研究稳态输出电压误差与边界层的关系，滑模系数的选择原则，以及全局滑模系数的约束条件，文献［5］将精确反馈线性化与滑模变结构控制相结合，并在DC／DC变换器上进行了验证。文献［6］设计了一个工作频率在520 k Hz，基于自适应电压调节的数字滑模控制器DC／DC变换器。本文以Buck变换器为对象，研究了滑模电压控制的实现方法，并进行仿真和实验验证。

1 Buck变换器状态空间描述

图1为滑模电压控制的Buck变换器原理图，选取输出电压误差和输出电压误差的变化率为两个状态变量。

图1 SMC-Buck变换器原理图

在CCM电流连续模式下，状态变量可以表示为

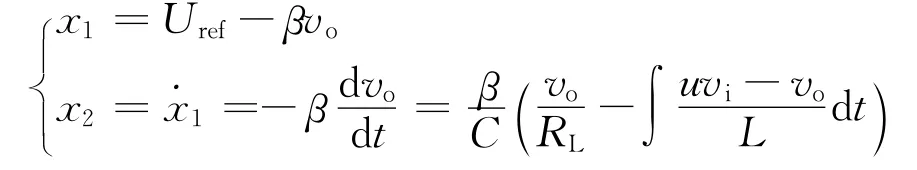
C，L，RL分别为电容、电感和瞬时负载电阻；uref和βvo分别为参考电压瞬时值和检测到的输出电压瞬时值；u=1或u=0为功率开关Sw的开关状态。将上述方程对时间求导，得到状态空间模型为

2 切换函数确定

在滑模控制中，控制器运用一个开关函数来确定系统的输入状态。对于滑模电压控制来说，开关函数u可以根据控制变量x1、x2，运用下面切换函数确定［7］。

式中，α为待设计的控制参数，称为滑动系数。

令σ=0，可得到斜率为-α的切换线，将相平面分为两个区域，每个区域对应着一个开关状态，开关状态引导相轨迹向切换线移动。对于降压变换器的2阶系统，控制律的基本形式为

式（4）的控制律使系统运行轨迹趋向切换线的一般性要求得到满足，然而，为确定系统运动轨迹维持于滑动线上，系统必须遵守由李雅普诺夫定理推导出系统渐进稳定性的存在条件，即

将式（3）对时间求导代入上式，可得到滑模控制存在的条件为

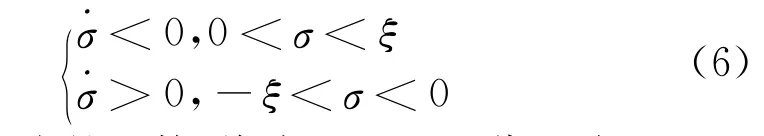
式中，ξ为任意小的正数，将式（2）和（4）代入式（6），不等式变为

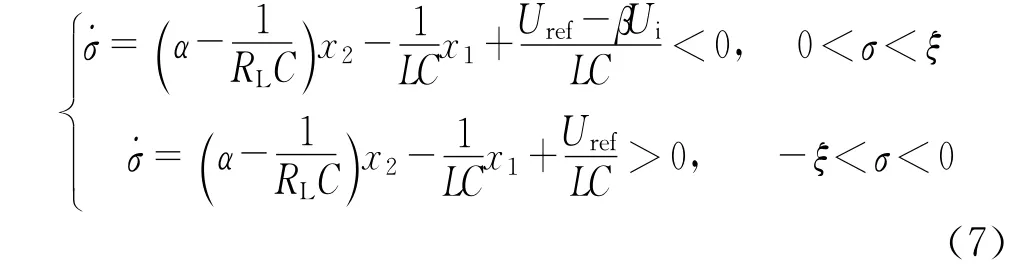
此外，求解式（3），可以得到

式中，x1（t0）为任意时刻t0的电压误差。从此式可以看出，在滑模控制器设计过程中，α的选择需综合考虑存在条件和一阶时间常数τ=1／α的动态响应问题。

因此，为了使系统既具备快速的动态响应又具有足够大的滑动模态区，将α设置为式（9）比较恰当，注意α必须为正。

3 SMC-Buck变换器的仿真与实验

3.1 实验设计

在实际中，为了解决理想滑模控制开关频率无限高和抖振的问题，便于变换器的设计和元器件的选择，必须对变换器的开关频率加以限制。控制变换器的开关频率，可以引入边界条件和滞环，将式（4）的控制律重新定义为：

但采用滞环限制开关频率，会产生变化的开关频率，给变换器的设计带来困难。为此，必须明确滞环宽度κ和开关频率fs之间的关系。滞环较宽时，开关频率低，跟踪误差大；滞环较窄时，跟踪误差小，但开关频率高，开关损耗大。

为对前面所述的理论进行验证，SMC-Buck变换器设计参数如表1。

表1 Buck电路设计参数

图2滑模控制器主要由电压跟随器Ui，差分放大电路UV，UD和比较器构成的滞环US组成。与大多数常规方法一样，β为输出电压Uo检测增益。电流互感器与电容串联，检测电流iC。参数的计算是在连续导电模式下进行的，Ui的变换范围是13～30 V，ir的变换范围是0.5～4 A。纹波电压的最大峰值为50 mV。

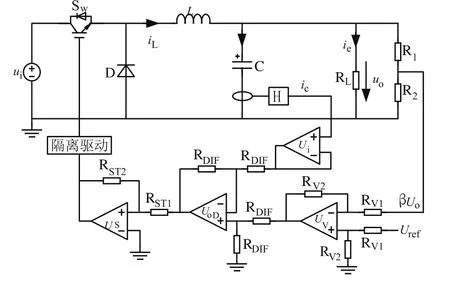
图2 标准SMC-Buck变换器

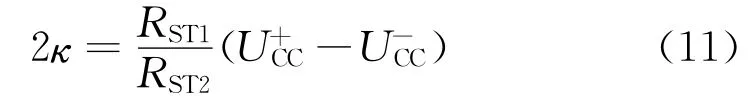
本设计中实际电感Lact=120μH，在额定参数相对不变的情况下，可以更换不同的电感值L使滞环宽度κ最好保持在0.1 VHz-1H-1≤κ≤0.2 VHz-1H-1范围内。

3.2 仿真研究

PSIM（Power Smulink）是电力电子领域针对性较强的专用仿真应用软件包；主界面中的电力电路、控制电路、传感器等模块库为电力电子电路的解析，控制系统的研究提供了强有力的仿真环境。同时其图形观

给定参考电压Uref=3.3 V，电阻RV2=20Ω，RV1=33 kΩ，RDIF=10 kΩ，RST1=110Ω，RST2=12 kΩ。用迟滞比较器来调节滞环宽度，U+CC和U-CC分别为比较器的正、负电源。测界面的Choose X-Axis Variable选项设置为分析非线性系统的相图绘制提供方便。

按照上述参数对SMC-Buck变换器进行了仿真，图3、4为在额定负载6Ω情况下，启动时波形，图4为切换线σ=0实际运行曲线，图5为两状态变量相图。

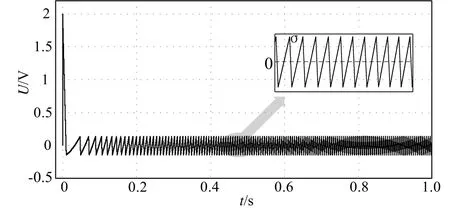
图3 启动到稳态时SMC-Buck切换线

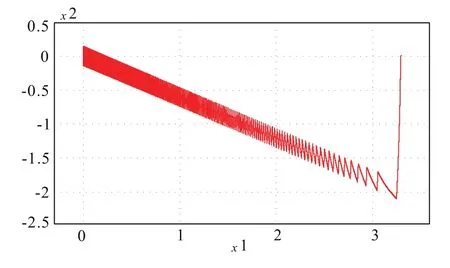
图4 两状态变量x1、x2相图

图5 负载变化时,输出电压、电流曲线

图5为负载6Ω突到3Ω时，仿真的输出电流电压曲线，可见当负载发生较大扰动时，控制对象输出电压基本保持不变，保持很强的鲁棒性。

3.3 实验结果

图6为SMC-Buck实验结果，右侧图为左侧的放大视图，四通道中ch1为输入电压，ch2为开关管Sw的驱动电压vgs；ch3为实验中切换线运动轨迹，可见在穿越切换线σ=0时，开关管Sw关断状态改变。实验输入24 V，输出12 V，满足期望要求，验证了对滑模变结构控制方法理解的正确性。

图6 SMC-Buck实验结果

4 结 论

滑模控制是一种优越的开关反馈控制系统，应用在开关变换器上可以达到很好的效果。本文将滑模变结构理论在Buck变换器上进行了实践，滑模电压控制器设计和实现比较简单，参数可以用数学公式精确地计算出来。通过仿真实验结果来看，滑膜变结构控制器是在大信号变换器模型的基础上设计的，具有较强的稳定性和鲁棒性。

［1］高为炳.变结构控制的理论及设计方法［M］.北京：科学出版社，1996.

［2］刘金琨.滑模变结构控制MATLAB仿真［M］.北京：清华大学出版社，2005.

［3］倪 雨，许建平.准滑模控制开关DC-DC变换器分析［J］.中国电机工程学报，2008，28（21）：1-6.

［4］倪 雨，许建平，王金平，于海坤.滞环调制全局滑模控制Buck变换器设计［J］.中国电机工程学报，2010，30（21）：1-6.

［5］乐江源，谢运祥，洪庆祖，张 志，陈林.Boost变换器精确反馈线型化滑模变结构控制［J］.中国电机工程学报，2011，31（30）：16-23.

［6］Guannan Xu，Chen Jia，Chun Zhang，Zhihua Wang.A digital sliding mode controller for switching power supply converter［C］.IEEE 9thInternational Conference on Digital Object Identifier，2011：994-997.

［7］R Venkataramanan，A Sabanovic，S Cuk.Sliding mode control of DC-to-DC converters［C］.Proceedings IEEE Conference on Industrial Electronics，Control and Instrumentations，1985：251-258.

［8］Siew-Chong Tan，Yuk-Ming Lai，Chi Kong Tse.Sliding mode control of switching power converter techniques and implementation［M］.Florida：CRC press，2012.