基于灰色模糊层次分析的电能质量综合评估

王忠民，高 峰，唐丹红，郭 磊

（国网上海市电力公司金山供电公司，上海200540）

电能质量评估指标众多，对单个指标进行评估具有片面性，评估结果不能够反应总体情况。因此，需要对电能质量进行综合评估。而综合评估的关键是要找到一种简单实用、正确高效的方法。

目前，综合评估的方法有数据包络分析法、突变决策法、概率统计和矢量代数法等［1］。文献［2］针对电能质量指标的特征，从概率统计的角度进行评估。文献［3］则将突变决策法用来进行电能质量综合评估，方法简单，但它将所有指标的重要性等同，没有突出重要指标的影响。

传统AHP法的判断比较极端，没有考虑到人在做出判断时的模糊性，得出的结论往往存在偏差，不够准确［4］。

本文将三角模糊数引入到传统AHP中形成FAHP法，确定电能质量指标的权重，通过灰色关联分析计算各指标的灰色关联系数，将两者加权求和进行综合评估，案例分析证明了本文方法的正确性。

1 电能质量的指标结构

电能质量的技术性指标有：电压质量、频率质量和供电可靠性，其中，供电可靠性主要体现在停电时间的长短上［4］，建立相应的指标层次结构如图1所示。

图1 指标层次结构

2 模糊层次分析法

在现实中，当人们进行决策判断时，常会出现模糊不清的现象。而传统AHP进行比较判断时比较极端，没有考虑人做出判断时的模糊性［4］。因此，本文将三角模糊数和传统的AHP算法［5］相结合，形成模糊层次分析法（FAHP），提高了判断的准确性。

2.1 三角模糊数

如果数M的隶属度函数μM：R→［0，1］表示为：

式中，l≤e≤p，e为M 的中值，则称M（l，e，p）为三角模糊数。M（l，e，p）的运算法则见文献［5］。

2.2 建立模糊判断矩阵

设对于上层某一指标，本层有m个指标与其相关。将这m个指标互相比较打分，建立如下模糊判断矩阵B。

式中，bij=（lij，eij，pij）为指标i相对于指标j的重要程度判断。

2.3 权重的计算

在专家打分，形成模糊判断矩阵后，就可以通过该矩阵进行指标权重的计算，可通过公式（2）、（3）计算指标i的权重大小。

式中，Qi为指标i的权重向量。

对公式（2）得到的三角模糊数Qi（li，ei，pi）做如下处理：

wi即为指标i的权重。

3 灰色关联分析

灰色关联分析是灰色系统理论中应用较为广泛的方法［6］，它可以比较不同因素相对于某一标准的贴近程度，关键是计算灰色关联度，计算步骤如下：

（1）设有n个对象，每个对象有m个指标，表示如下：

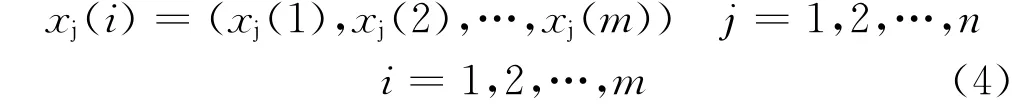
将其写成如下矩阵形式：

本文取x0（i）=（1，1，…，1）作为参考数列。

（2）计算灰色关联系数δ（x0（i），xj（i））

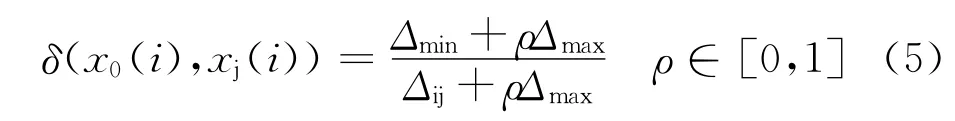
式中，Δij=|x0（i）-xj（i）|；ρ为分辨系数，一般取0.5。（3）计算灰色关联度ζ（x0，xj）

式中，wi为指标i的权重。

根据ζ（x0，xj）的大小对各方案进行排序。

4 灰色模糊层次分析法电能质量评估

将模糊层次分析法和灰色关联分析相结合，形成灰色模糊层次分析法来对电能质量进行综合评估，步骤如下：

（1）确定评估指标层次结构。如图1所示。

（2）确定参考数列x0（i）=（1，1，…，1）。

（3）归一化处理。本文采用相对优属度进行归一化处理［4］。

a.固定型指标

如：电压波动、三相不平衡等。相对优属度ηij为：

式中，fij为检测点j的第i个指标；fi0为指标i的最佳值；σi=max|fij-fi0|。

b.区间型指标

如电压偏差等。相对优属度ηij为：

式中，fdi、fui为指标i最佳值的下界和上界；βi=max｛fdi-fimin，fimax-fui｝。

c.成本型指标

如：谐波含量、停电时间等。相对优属度ηij为：

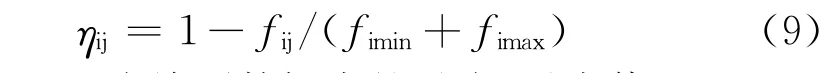
式中，fimin、fimax为检测数据中的最小、最大值。

（4）相对优属度矩阵η

按照式（7）～（9）进行归一化处理，形成相对优属度矩阵η：

（5）确定评估矩阵。将相对优属度矩阵η代入公式（10）中，可以得到第j个检测点的电能质量和参考数列比较时，第i个指标的灰色关联系数δj（i）为：

（6）通过FAHP法确定各指标权重W。

（7）综合评估

根据公式（11）计算灰色关联度。

ξ即为评估结果向量。

5 案例分析

表1为某地区5个监测点的电能质量数据。表2为各指标的等级界限［9］。应用本文方法对该地区5个点的电能质量进行综合评估。

表1 实测数据

为了能够从结果中判断出各检测点的等级，本文将各项指标的等级界限也当做检测数据处理。根据文中第4节的步骤3～5，最终可得到关联系数矩阵δ：

根据FAHP法得到各项指标权重为：

综合评估向量ξ为：

向量ξ中前四个数为Ⅰ～Ⅳ等级界限的评估值。ξ后面五个数为各检测点的评估值。从中可以看出5个点的电能质量优劣顺序为：

Ⅰ＞检测点2＞Ⅱ＞检测点5＞检测点4＞检测点3＞Ⅲ＞检测点1＞Ⅳ

可以得出以下结论：检测点1的电能质量为Ⅳ级，检测点3、4、5的电能质量均为Ⅲ级，检测点2的电能质量为Ⅱ级。

另外，根据本文方法还可以看出检测点3、4、5虽然等级都为Ⅲ级，但检测点5的电能质量要好于检测点4，检测点4的电能质量要好于检测点3。本文方法不但可以确定检测点的等级，而且对于相同等级的检测点也可以比较出优劣。

表3为应用不同方法得到的评估结果。

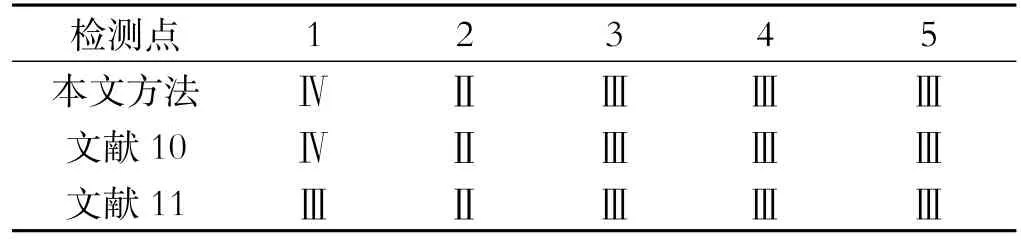
表3 评估结果比较

从上表中可以看出应用本文方法和文献10中的组合赋权法得出的评估结果是一样的，和文献11的结果略有差异。可见，本文方法得到的评估结果是可信的。

6 结 论

本文将三角模糊数和层次分析法结合形成FAHP法，确定各电能质量指标的权重，并通过灰色关联分析法计算出各指标的关联系数。最后，将两者加权求和进行综合评估。该评估方法简单、正确、实用。

［1］付学谦，陈皓勇.基于加权秩和比法的电能质量综合评估［J］.电力自动化设备，2015，35（1）：128-132.

［2］江 辉，彭建春，欧亚平，等.基于概率统计和矢量代数的电能质量归一量化与评价［J］.湖南大学学报：自然科学版，2003，30（1）：66-70.

［3］曾 正，杨 欢，赵荣祥.基于突变决策的分布式发电系统电能质量综合评估［J］.电力系统自动化，2011，35（21）：52-57.

［4］康世崴.基于模糊层次分析的电能质量综合评估［D］.长沙：湖南大学，2010.

［5］曹婷婷.基于模糊层次分析法与灰色关联分析的服务外包供应商选择方法研究［D］.沈阳：东北大学，2012.

［6］黄贯虹，方 刚.系统工程方法与应用［M］.广州：盛南大学出版社，2005.

［7］邓聚龙.灰色预测与灰色决策［M］.武汉：华中科技大学出版社，2002.

［8］Kaufman A，Gupta M M.Introduction to fuzzy arithmetic theory and application［M］.New York：Van Nostrand Reinhold，1991.

［9］肖湘宁，韩民晓，徐永海，等.电能质量分析与控制［M］.北京：中国电力出版社，2004.

［10］李连结，姚建刚.组合赋权法在电能质量模糊综合评估中的应用［J］.电力系统自动化，2007，37（4）：56-60.

［11］王 鹤，曾 鸣，陈 珊，等.基于模糊层次分析法的供电服务质量综合评价模型［J］.电网技术，2006，30（17）：92-96.

［12］谭家茂，黄少先.基于模糊理论的电能质量综合评价方法研究［J］.继电器，2006，34（3）：55-59.