有限混合非对称Laplace分布的渐近分布

黄建文，庹中友，刘衍民(遵义师范学院数学与计算科学学院，贵州遵义563002)



有限混合非对称Laplace分布的渐近分布

黄建文，庹中友，刘衍民
(遵义师范学院数学与计算科学学院，贵州遵义563002)

摘要:设是独立同分布的随机变量序列并且共同的分布函数是混合非对称Laplace分布.表示的部分最大值.表示部分最小值.作者主要研究同服从混合非对称Laplace分布的独立随机变量序列最大值和最小值的分布的渐近分布以及相应的赋范常数.

关键词:非对称Laplace分布;混合分布;渐近分布;赋范常数

随着概率论与数理统计的不断发展，有限混合分布的应用也逐渐深入，例如应用在医学、农学、畜牧学、地理学和遗传数据分析等各个领域，因此，有限混合分布的极值理论便成为我们目前主要的研究对象，其结论将会为以后混合分布的更深入的研究提供方便.

有限混合分布(Finite Mixed Distributions)在现代统计的整个发展过程中作为一个模型得到了广泛的研究和应用.

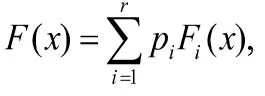
Mladenovic[2]给出了由两个指定的分布构成的混合分布的极值理论，即混合正态分布混合柯西分布、均匀与截断指数分布的混合.Chen Qiong和Peng Zuoxiang[3]将上面的结论分别推广到有限混合分布与等价类的情形.

非对称Laplace分布主要应用在贝叶斯分位数回归、审查的基因表达数据、商务智能和金融工程、基因选择和分类方法、经济行为和组织、分派和货币速度、模拟摆圆形数据、模拟金融时间序列、利率和货币兑换数据等方面,详细内容请看参考文献[4-6].

本文给出在独立同分布情况下，由两个指定的分布以及有限个指定的分布构成的混合分布的渐近分布和相应的赋范常数，其中，指定的分布是非对称Laplace分布.

符号说明：

首先给出有限混合分布的定义如下:

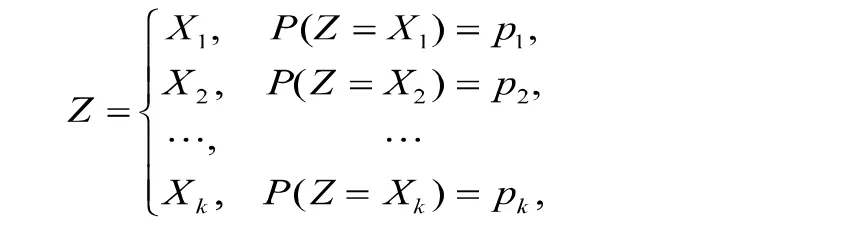
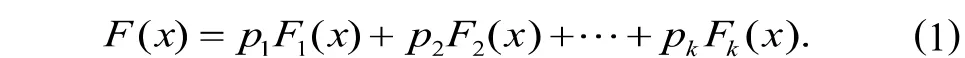
特别地，当k=2时，

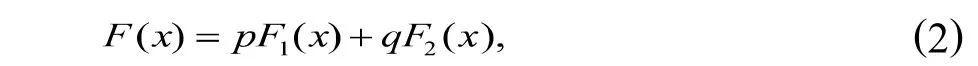
然后，我们给出非对称Laplace分布的定义.

定义1设随机变量X的概率密度函数和累积分布函数分别是

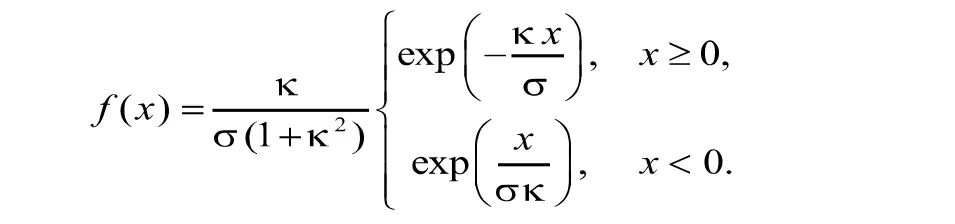
和

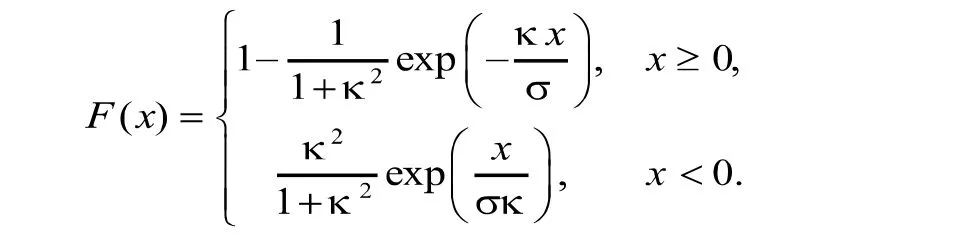
首先，我们给出由两个指定分布构成的混合分布的渐近分布以及相应的赋范常数.

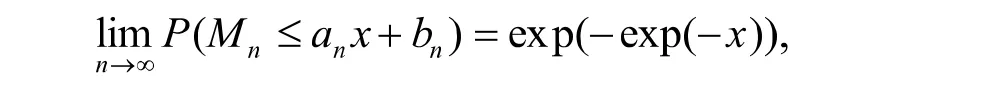
其中，

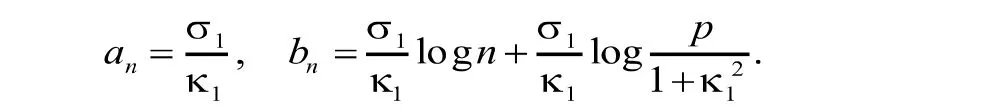
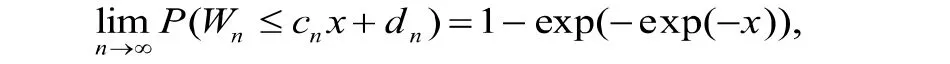
其中，

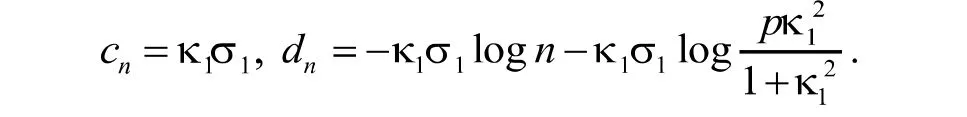
下面，我们将上述结果推广到由有限个分布构成的混合分布的情形.

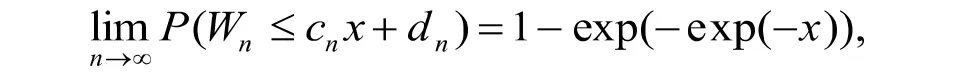
其中，

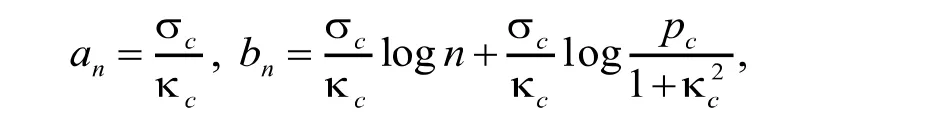
其中，

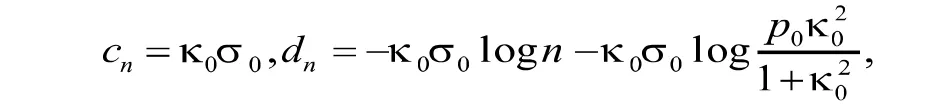
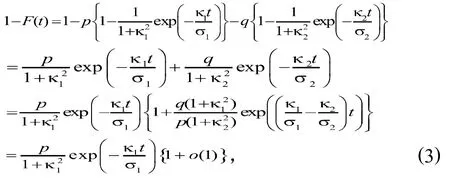
由(3)式可得，

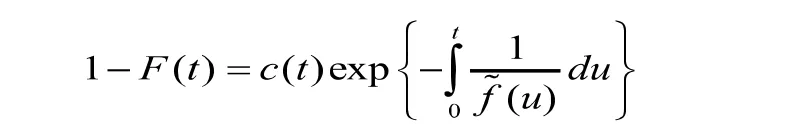
并且

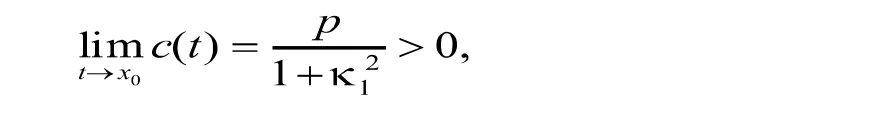
因此，根据命题1.4[7]，得到

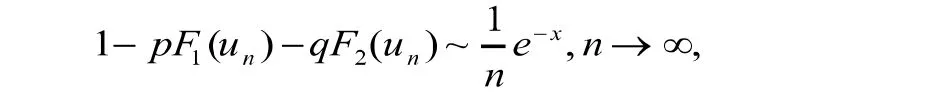
再由(3)式，则有

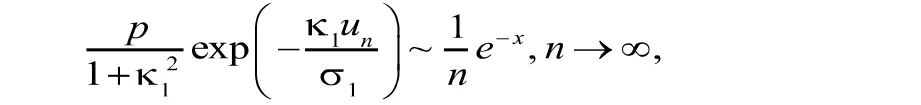
因此，

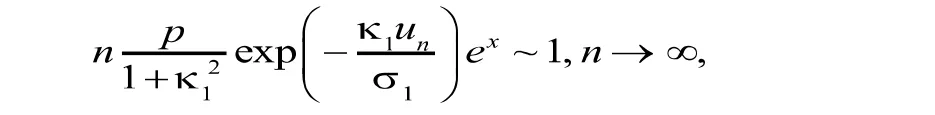
从而，

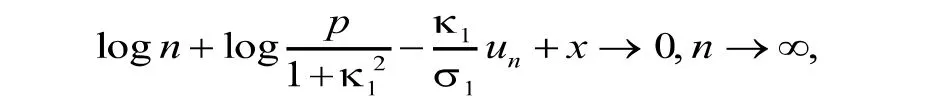
所以，

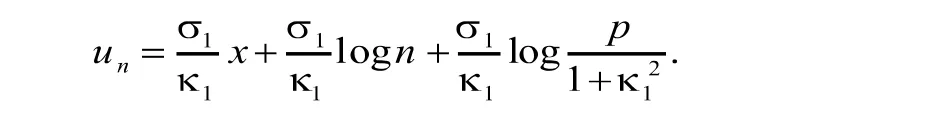
当t＜0时，证明方法与t≥0时类似，结合Galambos中定理2.1.6[8]，就可以得证.

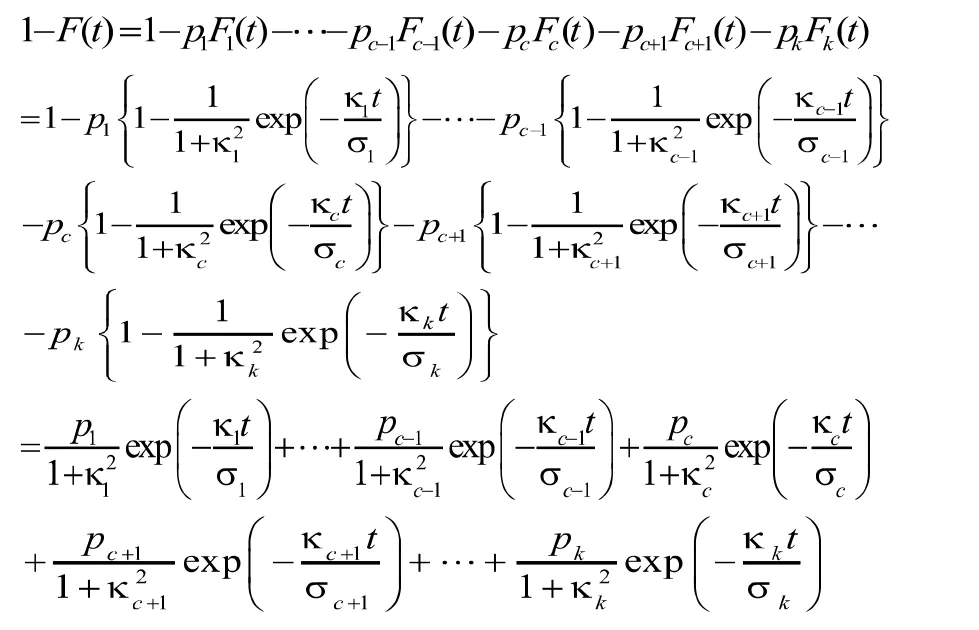
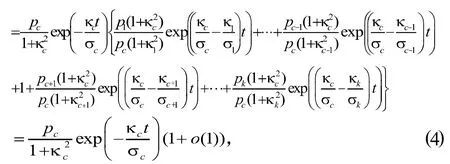
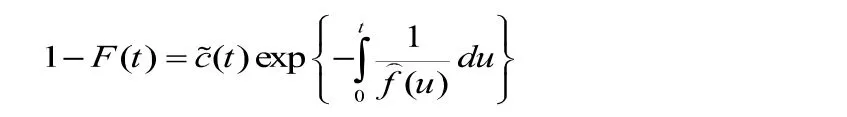
并且

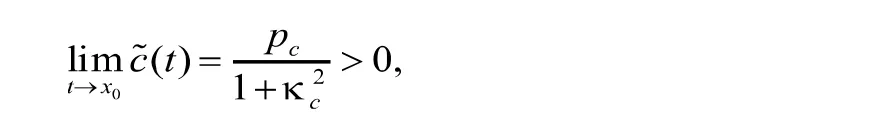
因此，根据命题1.4[7]，得到对于赋范常数an和bn的求解，方法与定理1的证明类似，这里就不作详尽推导了.

对于t＜0，证明方法与t≥0的情形类似，结合Galambos中定理2.1.6[8]，就可以得证.

参考文献：

[1]Nelson D B.Conditional heteroskedasticity in asset returns: A new approach[J].Econometrica,1991,59(2): 347-370.

[2]Mladenovic P.Extreme Values of the Sequences of Independent Random Variables with Mixed Distributions[J]. Matematicki Vesnik,1999,51(1-2):29-37.

[3]Cheng Q,Peng Z.Limiting distributions of maxima on mixed distributions[J].西南大学学报(自然科学版),2011,33(1):5-10.

[4]Jayakumar K,Kuttykrishnan A P.A time-series model using asymmetric Laplace distribution[J].Statistics and Probability Letters. 2007,77(16):1636-1640.

[5]Johnson N L,Kotz S,Balakrishnan N.Continuous Univariate Distributions[M]. New York:John Wily and Sons, 1995.

[6]Kozubowski T J,Podgorski K.A class of asymmetric distribu tions[J].Actuarial Research Clearing house,1999,(1): 113-134.

[7]Resnick S I.Extreme value,Regular Variation,and Point Processes[M].New York:Springer-Verlag,1987.

[8]Galambos J.The Asypmtotic Theory of Extreme Order Statistics[M].New York: Wiley,1987.

（责任编辑：朱彬）

The asymptotic distribution of finite mixture asymmetric Laplace distribution

HUANG Jian-wen,TUO Zhong-you,LIU Yan-min
(School of Mathematics and Computational Science,Zunyi Normal College,Zunyi 563002，China)

Abstract:Letbe an independent and identically distributed random sequence with common distribution Fobeying mixture asymmetric Laplace distribution.denotes partialmaximum.denotes partial minimum. In this paper, the asymptotic distribution of distribution of the maximum and minimum of independent identically distributed random variable sequence with mixture asymmetric Laplace distribution and associated normalizing constants are studied.

Key words:asymmetric Laplace distribution; mixed distribution; asymptotic distribution; normalizing constants

作者简介：黄建文，男，甘肃甘谷人，遵义师范学院数学与计算科学学院助教，硕士，主要从事极值统计分析的研究。

基金项目：国家自然科学基金资助项目（NO.71461027）；贵州省自然科学基金资助项目（黔科合J字LKZS[2014]22号，黔科合J 字LKZS[2014]29号）

收稿日期：2015-5-12

中图分类号：O211

文献标识码：A

文章编号：1009-3583（2015）-0090-03