导管调距桨实效伴流分数的简化CFD计算

张 弘刘爱兵邹 义刘 艳李海涛

（1.大连理工大学船舶工程学院，大连116024；2.中国船舶重工集团公司第704研究所，上海200031；3.大连理工大学能源动力学院）

导管调距桨实效伴流分数的简化CFD计算

张 弘1刘爱兵2邹 义2刘 艳3李海涛1

（1.大连理工大学船舶工程学院，大连116024；2.中国船舶重工集团公司第704研究所，上海200031；3.大连理工大学能源动力学院）

为了获得实效伴流分数和推力减额系数，一般情况下要进行船桨自航实验。在导管调距桨的自航实验中，由于需要测量导管的推力以及调节螺距比，会增加实验的复杂程度。近年来，数值水池的应用得到了广泛关注。但由于计算模型通常为整条船和桨，几何模型复杂且计算量大。针对船体较长且具有平行中体的船舶，本文探索了一种简化模型方法即考虑半个船模和桨，忽略船首对尾部半流的影响。与实验结果比较，满载和压载工况下计算得到的伴流分数误差均约在4%左右。本文的研究表明在缺少实验条件的情况下，简化模型的CFD方法可以作为研究伴流分数的有效手段。

导管调距桨 自航试验 简化模型 CFD 伴流分数

0 引言

研究螺旋桨性能时，不仅需要考虑螺旋桨的敞水性能，同时还要考虑船体对螺旋桨产生的影响。在敞水中，桨前的来流是均匀的，桨在船后时，由于桨和船体的相互影响，桨前伴流不均匀，这样，桨的水动力性能和空化性能就与敞水性能不一致。船后伴流分为标称伴流和实效伴流，其中标称伴流一般不考虑螺旋桨对船体尾部流场的影响，而实效伴流则考虑，因此，通常所说的伴流分数指的是考虑螺旋桨工作时的实效伴流分数。船模自航试验所得到的结果为实效伴流分数。

目前CFD技术日趋成熟，已成为预报螺旋桨敞水性能、自航性能的重要研究方法。华中科技大学的杨琴等人［1］采用CFD方法对SUBOFF潜艇模型的自航性能进行了研究，对全附体的艇体的压力分布进行了仿真，获得了合理的结果。哈尔滨工程大学的赵大刚等人［2］利用STAR-CCM软件对带自由表面的KCS船桨模型的水动力性能进行了预报，与试验值吻合较好。702研究所的张楠等人［3］采用了VOF方法对带有自由液面的艇／桨干扰特性进行了研究，计算了桨在艇后的推力扭矩并与试验进行对比，验证了计算的可靠性。哈尔滨工程大学的郭春雨等人［4］通过统计的方法，研究了不同船型系数，螺旋桨参数对实效伴流分数的影响。海军工程大学的袭鹏等人［5］采用CFD方法对多桨船舶的自航因子进行了数值预报，分析了数值计算的可靠性以及各个螺旋桨的性能。

由上面文献中的研究方法可以看出，采用CFD方法研究船桨匹配问题时绝大多数计算模型都是考虑整条船和桨。这样既可以得到船模阻力又可以得到船后螺旋桨的性能，获得办理分数和推力减额分数，进而评估船和桨的匹配性能。但是这种建模方式所需网格数量巨大，需要大量的计算时间。如果无需分析船模阻力，只考虑船尾伴流对桨性能的影响，只对船体后半部分以及螺旋桨进行研究是一种可取途径。可以认为，如果船体较长且具有平行中体，尾部伴流受船首的影响较小，此种情况下，这种简化的模型即半个船体和桨放在一起计算是可行的，可以研究实效伴流对桨性能的影响。基于此，本文采用STAR-CCM软件研究船后伴流对某导管调距桨桨性能的影响，进而获得实效伴流分数和推力减额分数，并与自航试验数据进行比较验证简化模型的可靠性。

1 计算模型

1.1 船体模型

实船船长为108 m，设计吃水为6.9 m，螺旋桨直径为4.25 m，自航试验采用30∶1的缩尺比，而敞水试验采用17∶1的缩尺比。为了简化计算，对船体作如下简化：

（1）去掉船体的前半部分，不考虑船首，选择从第十站开始的后半部分模型；（2）去掉水线面以上部分，不考虑自由液面的影响；（3）导管支架对桨盘的流场影响很小，忽略其影响；（4）不考虑舵的影响。图1显示的是简化的船和桨几何模型。图2是放大的船尾部分模型。

图2 船体尾部螺旋桨模型（左）和实物（右）Fig.2 Propeller model（left）and actual object（right）installed at the stern

1.2 螺旋桨模型

试验所使用的螺旋桨是中国船舶重工集团公司第704研究所设计的导管调距桨，其中导管为37导管，其剖面形状如图3所示，桨叶为侧斜桨，实桨直径为4.25 m，导管与桨的间隙为0.1%D（D为桨的直径）。自航试验缩尺比为30∶1，模型桨的直径为141.7 mm，自航试验螺距比为1.31，模型示意如图4所示（实物见图2）。

1.3 计算域和计算方法

本文选取了两种工况进行研究，分别是满载和压载，其中满载的实船吃水为6.9 m，换算到船模上为230 mm；压载的实船吃水为4.8 m，换算到船模上为160 mm。

图4 计算导管螺旋桨模型图Fig.4 Computational model of the ducted propeller

两种工况下的计算域均为长方体，如图5所示，左端面为入口，右端面为出口，其中船底部到下壁面距离为1倍船长，船尾到后端面为2倍的船长，船侧到计算域侧壁面距离为0.5倍的船长。由于螺旋桨旋转，因此计算动域选取为桨周围的一个圆柱，圆柱表面和周围静止域交界面就是动、静交界面。

计算中，入口给定均匀速度，出口给定压力，上端面为水线面，此面采用对称面。下壁面以及侧壁面采用滑移壁面。数值计算是通过使用软件STAR-CCM完成的，湍流模型选用Realizable k-ε两方程模型，定常计算。网格总数为400万。

图5 满载（左）与压载（右）计算域模型Fig.5 Computational domains for full load（left）and ballast（right）conditions

2 自航试验简介

船模自航试验是在大连理工大学船舶工程学院拖曳水池中进行的，采用自航动力仪测量船体和螺旋桨的相关参数。由于是导管桨，测量导管推力的导管测量臂需要穿过船体，给密封增加了一些难度。试验装置图如图6所示。

图6 自航试验照片Fig.6 Picture of self-propulsion test

3 计算结果和分析

下面给出导管螺旋桨的推力系数（KT）、扭矩系数（KQ）和效率（η）的计算公式：

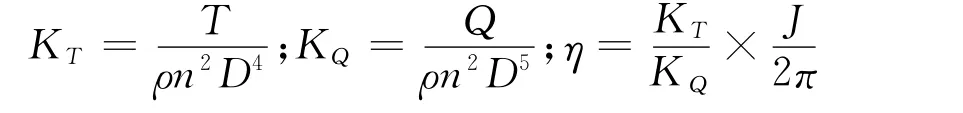
其中T为总推力，Q为扭矩；J＝VA／n D，为进速系数，式中VA为进速；n为螺旋桨转速；D为螺旋桨直径。对于导管的推力系数，将公式中的T用导管推力TN代替。

3.1 满载工况

表1给出了不同航速时船模自航试验测得的和数值模拟计算获得的推力和扭矩。表1中的Vm是拖车的速度也就是试验来流速度，Vs是实船的航速。由表1可以看出，与试验值相比，推力计算值的平均误差为6.227%，扭矩计算的误差除了进速最小的那个工况误差较大外，其余工况的比较小，尽管如此，计算扭矩的平均误差为5.341%。从计算结果与试验值的误差来看，用简化的几何模型计算自航试验，得到的结果还是比较可靠和可信的。这种简化模型大量减小了网格数量，使得计算速度大幅提升，可用于数值研究船舶的自航试验，为验证螺旋桨性能和桨优化设计提供指导。

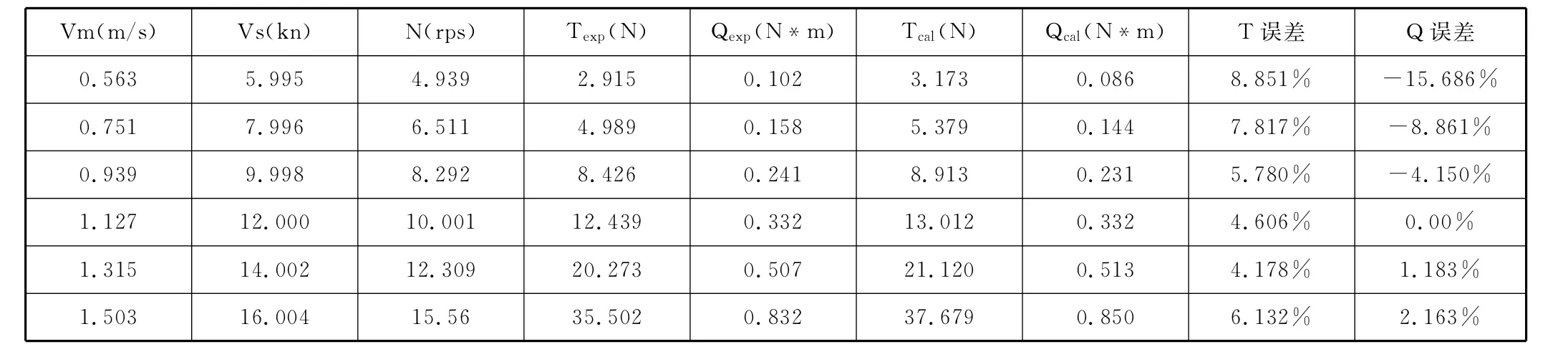
表1 满载工况时自航试验结果和k-ε模型计算结果Table 1 Self-propulsion test data and numerical results fromthe k-εmodel at the full loading condition

为了获得试验伴流分数，需要用到自航试验和敞水试验两个试验结果。具体步骤是在敞水性能的推力系数曲线上找到每个自航点的推力系数，得到该推力系数对应的敞水试验的进速，根据此进速和自航点的进速进而获得伴流分数。

敞水性能试验是在大连理工大学船舶工程学院试验水池进行的，导管桨试验模型图如7所示，缩尺比为17∶1。

图7 敞水试验模型及试验照片Fig.7 Open water test model and test picture

图8给出了螺距比为1.309时螺旋桨的敞水性能试验结果。按照前面所述方法得到相同推力系数时的敞水进速，继而获得伴流分数w（ω＝1－D），结果见表2。

由表2可以看出，在小进速和大进速工况，CFD得到的伴流分数误差比较大，中间进速误差较小，但平均预测误差为3.29%，小于10%，工程上是可以接受的。另外由于伴流分数数值较小，对误差比较敏感，因而导致伴流分数的计算值的与真实值附近上下偏移。

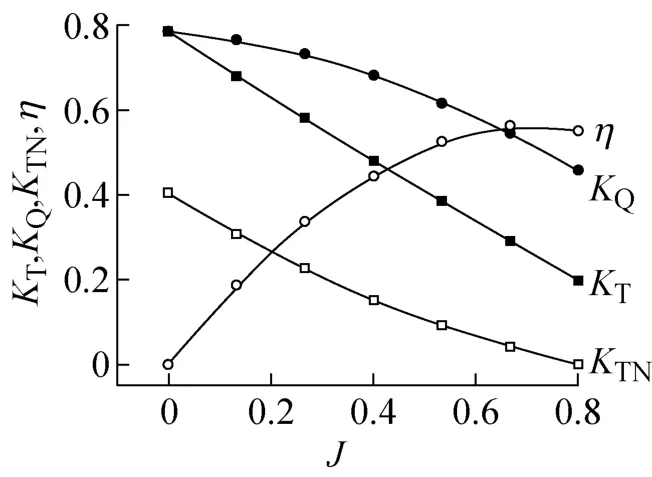
图8 敞水试验结果Fig.8 Open water test results

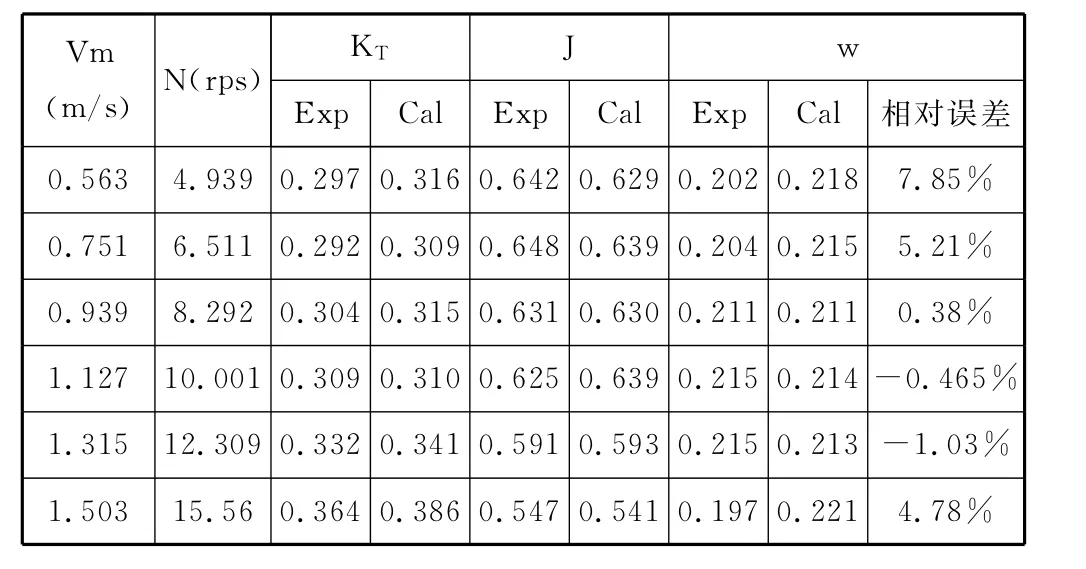
表2 满载工况下伴流分数试验值和CFD计算结果比较Table 2 Comparison of experimental and predicted wake fractionsat the full loading condition

3.2 压载情况下的计算结果

压载工况下的水线面更靠近螺旋桨。表3给出了自航试验不同工况下导管桨总推力、扭矩的试验值和CFD计算结果以及相应的计算误差。由该表得到CFD计算得到的总推力、扭矩的计算误差分别为4.02%和4.09%，计算准确度与满载工况相当，进而说明本文的简化计算策略合理和可靠。

表3 压载工况试验和计算结果Table 3 Test and calculated results at the ballast condition

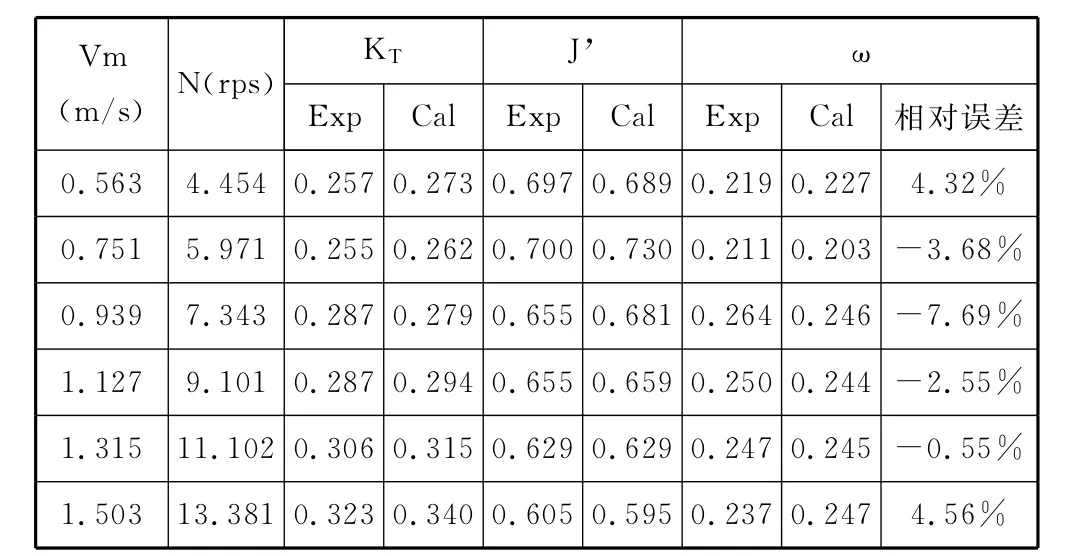
表4 压载工况下试验和计算的伴流分数结果Table 4 Experimental and predicted wake fractionsat the ballast condition

采用满载工况的计算方法，同样可以得到压载工况的伴流分数，计算结果如表4所示。

由表4可以看出，压载工况下的伴流分数计算误差在10%内，基本满足工程需要。

3.3 满载与压载工况下桨前流场比较

图9显示的是满载、压载和敞水工况下，来流速度均为Vm＝1.127 m／s时，桨前8%D截面的轴向速度云图。与敞水工况下的云图比较，可以发现：满载和压载工况下船后螺旋桨前的流场较相似但不均匀，满载工况的流场周向变化更加剧烈，对桨性能带来不利影响。

图9 不同工况下桨前某截面速度分布云图Fig.9 Velocity distribution contours at a plane upstream of the propeller for different conditions

4 结论

本文通过试验和简化的CFD方法对某节能型大型远洋渔船的导管调距桨桨进行了自航和敞水性能研究，得到如下结论：

（1）采用半个船体模型的CFD策略，获得了合理的满载和压载工况下的螺旋桨性能参数以及伴流分数。计算结果与试验值吻合较好，精度符合工程要求。说明简化的处理方法是可行的。因此对于具有平行中体且船长较长的船舶，可以采用半个船体模型的CFD方法进行自航数值试验，既能节约计算资源又能快速获得船后桨的性能，为评估船桨匹配提供有价值的参考。

（2）对于采用导管桨或者导管调距桨的渔船、拖船等船舶，在测量导管推力较为困难的自航试验中，可以采用这种简化模型来得到导管推力。

（3）由于本文采用简化模型，只考虑了部分船长且没有考虑自由液面的影响，所以不能用来计算船模阻力。此外，本文的计算精度可以通过非定常计算进一步提高，这是未来要做的工作。

［1］ 杨 琴，王国栋，张志国，冯大奎，王先洲.基于CFD的潜艇模型自航仿真分析［J］.中国舰船研究，2013（2）：22-27.

［2］ 赵大刚，郭春雨，邹 泽.带自由表面的船桨系统水动力性能理论计算［A］.中国造船工程学会.第十二届全国内河船舶与航运学术会议论文集［C］.中国造船工程学会，2012：9.

［3］ 张 楠，张胜利，沈泓萃，谢 华.带自由液面的艇／桨干扰特性数值模拟与验证研究［J］.水动力学研究与进展A辑，2012（1）：94-99.

［4］ 郭春雨，陈月钢，王成尧，谷双泰，刘桂杰.肥大型船舶实效伴流分析及预报［J］.船海工程，2014（4）：47-50＋54.

［5］ 袭 鹏，熊 鹰，邱辽原，王展智.多桨船舶自航因子数值预报［J］.中国舰船研究，2014（6）：59-64＋99.

［6］ 盛振邦，刘应中.船舶原理（下册）［M］.上海：上海交通大学出版社，2004.

［7］ 初绍伟，邹早建，曲宁宁.船后伴流场影响因素的数值研究［J］.武汉理工大学学报（交通科学与工程版），2013（5）：1026-1030.

［8］ 程宣恺，周志勇，陈 康，魏菲菲，陆琛亮.船模自航试验数值模拟研究［J］.船舶与海洋工程，2013（3）：10-15.

［9］ CHOI J E，MIN K S，KIM J H，et al.Resistance and propulsion characteristics of various commercial ships based on CFD results［J］.Ocean Engineering，2010，37（7）：549-566.

Simplified CFD calculations for the effective wake fraction of ductedcontrollable pitch propellers

Zhang Hong1Liu Aibing2Zou Yi2Liu Yan3Li Haitao1
（1.School of Naval Architecture，Dalian University of Technology，Dalian 116024，China；2.Shanghai Marine Equipment Research Institute，Shanghai 200031，China；3.School of Energy and Power Engineering Architecture，Dalian University of Technology，Dalian 116024）

Self-propulsion tests of a ship and a propeller are generally required in order to obtain effective wake fractions and thrust reduction coefficients.For ducted controllable-pitch propellers，the complexity of measurement is increased because of the need to measure thrust of the duct and to adjust the pitch ratio.Application of numerical towing tanks have been attracted attention in recent years.However due to the computational domain involving the whole hull and propeller，the geometrical model is complex and the amount of computation is huge.For a long ship with a parallel middle body，a simplified ship model involving only half of the ship and a propeller is explored in this paper.The effect of the ship bow on the wake is ignored.Compared with measurements，an error for computed effective wake fractions is about 4%for both full loading and ballast conditions.This result shows that the current simplified method can be used to predict effective wake coefficients when lacking of experimental facility.

Ducted controllable-pitch propeller self-propulsion test simplified model CFD wake fraction

U664.33

A

1006-8244（2015）04-027-05

国家高技术研究发展计划（863计划）（2009AA045002）

张 弘（1991－），男，硕士研究生。研究方向为船舶水动力。