自同步牙嵌式离合器啮合机理建模及其啮合成功概率分析

李兴忠宋 斌童燕华郭丽丽雷雨龙

（1.杭州前进齿轮箱集团股份有限公司，杭州311203；2.吉林大学汽车仿真与控制国家重点实验室，长春130022）

自同步牙嵌式离合器啮合机理建模及其啮合成功概率分析

李兴忠1，2宋 斌1童燕华1郭丽丽1雷雨龙2

（1.杭州前进齿轮箱集团股份有限公司，杭州311203；2.吉林大学汽车仿真与控制国家重点实验室，长春130022）

通过对自同步牙嵌式离合器换档啮合过程的分析，分阶段建立了它的动力学模型，从概率角度描述了其换档成功与否这一不确定结果，建立了其换档啮合成功概率的数学模型，并通过Matlab／Simulink仿真分析了各档位换档过程中影响该概率的因素，确定了不同档位换档时的最优换档速差。最后通过台架实验验证了理论分析的正确性和准确性。分析结果可用于自同步牙嵌式离合器换档啮合过程控制策略的制定以及使用自同步牙嵌式离合器的变速器换档质量的改善和提高。

车辆工程 自同步牙嵌式离合器 建模 概率 扭转振动

0 引言

同步器在换档过程中不需要借助外部控制，而仅依靠自身零部件间的相互作用就可以达到同步，且其在啮合套与啮合齿轮转速达到同步前可以防止过早啮合从而减小换档过程中传动系统扭转振动，因此被广泛应用在机械式自动变速器（AMT）和双离合器自动变速器（DCT）中［1］。但其换档同步时间长、系统组成复杂，且随着控制技术的发展其在换档过程中不需要外部控制的优势不再明显。另外，重型商用车对换档舒适性要求不高，但要求自动变速器在换档过程中动力中断时间要短；电动车要求自动变速器结构简单、便于安装［2-3］。因而装配同步器换档系统的机械式自动变速器已不能满足重型商用车和电动车的使用要求。牙嵌式离合器换档系统因其换档时间短、结构简单、装配空间小、扭矩传递准确且容量大以及制造成本低等优点而成为重型商用车和电动车用自动变速器换档系统的首选［2-4］。

本文以某机械式自动变速器中使用的自同步牙嵌式离合器换档系统为研究对象，通过分析其啮合机理，对其换档啮合过程分阶段进行数学建模，利用Matlab／Simulink建立自同步牙嵌式离合器换档成功概率的仿真模型，研究影响该概率的因素，并通过模型计算确定各档位换档时啮合齿轮与啮合套间最佳速差，为换档过程中电机调速控制策略和算法的设计提供理论依据和参考。

1 自同步牙嵌式离合器换档系统

机械式自动变速系统是连同离合器从动盘（或驱动电机）、自动变速箱在内的综合控制系统，是一个复杂的多自由度、多质量系统，很难精确建模。为了建立有效的传动系统模型，首先进行了如下假设：

1）假设系统由无弹性的惯性元件组成；

2）每个旋转件只有一个自由度；

基于以上假设，机械式自动变速系统可简化为一个离散化的当量系统，将啮合齿轮（即目标档位齿轮）及其之前的参数或变量向啮合齿轮转化，与啮合齿轮对应的啮合套及其之后的参数或变量向该啮合套转化，其简化模型如图1所示，离合器从动盘或驱动电机通过花键与变速器输入轴连接传递动力。

2 自同步牙嵌式离合器啮合机理建模

自同步牙嵌式离合器换档系统是一种在啮合套与啮合齿轮之间存在转速差的情况下进行换档，利用啮合齿轮花键齿端面与啮合套花键齿端面直接接触摩擦完成啮合传递扭矩的换档系统。其换档啮合过程如图2所示，可以划分为初始自由滑行阶段、齿面撞击阶段、齿面摩擦阶段和花键啮合阶段4个阶段。

2.1 自同步牙嵌式离合器啮合过程动力学建模

2.1.1 初始自由滑行阶段

由于啮合套与啮合齿轮之间没有锁止机构，所以啮合套与啮合齿轮之间可以以任何一个角速度差Δω0开始换档。在啮合套花键齿端面与啮合齿轮花键齿端面接触前，离合器不传递任何扭矩，啮合套只

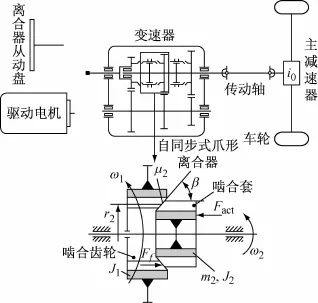
图1 机械式自动变速系统及自同步牙嵌式离合器模型Fig.1 The system of automated mechanical transmission and model of self-synchronization jaw clutch

图2 自同步牙嵌式离合器换档啮合过程Fig.2 Engagement process of self-synchronizer jaw clutch when shifting

需克服其内花键与花键毂外花键之间因扭矩损失造成的沿轴向滑动的摩擦力，这一阶段称为初始自由滑行阶段。

啮合套内花键与花键毂外花键之间沿轴向滑动的摩擦力大小如式1所示。

则啮合套初始自由滑行阶段所持续的时间为：

其中，μ1啮合套内花键与花键毂外花键间的摩擦系数，r1啮合套内花键平均半径；m2－啮合套质量；Tsloss啮合套及其与之相连的旋转部件的扭矩损失；Fμ1啮合套内花键与花键毂外花键间沿轴向的摩擦力，Fact作用于啮合套上的换档力。

由于啮合套与整车连接，可认为其角速度在换档过程中保持不变。因为齿轮搅油、轴承摩擦等原因造成的功率损失会使啮合齿轮及其与之相连的转动部件转速下降［5］，本文中认为该过程为匀减速过程。则可知初始滑行阶段结束时啮合齿轮与啮合套间的角速度差为：

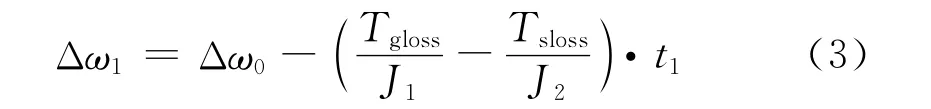
其中J1和J2分别为：

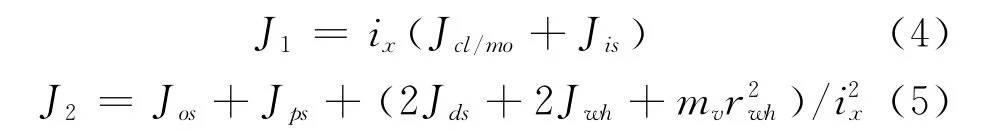
其中，Δω0、Δω1啮合过程各阶段开始时啮合齿轮与啮合套间角速度差；Tgloss啮合齿轮及其与之相连的旋转部件的扭矩损失；J1啮合齿轮等效转动惯量；J2啮合套等效转动惯量，t1、t2、t3、t4啮合过程各阶段结束时刻；Jis变速器输入轴转动惯量；Jos变速器输出轴转动惯量；Jps汽车主传动轴转动惯量；Jds驱动半轴转动惯量；Jwh驱动轮转动惯量；mv整车质量；rwh驱动轮滚动半径；Jcl／mo－离合器从动盘或电动机轴转动惯量。

2.1.2 齿面撞击阶段

当啮合套花键齿端面与啮合齿轮花键端面之间的法向距离达到10－4m时，端面间会形成油膜，此时端面间的摩擦为混合摩擦；当端面间的法相距离达到10－5m时，端面间的大部分润滑油被排出，摩擦过渡到固体摩擦阶段，此时认为啮合套花键齿与啮合齿轮花键齿发生直接撞击，啮合套的轴向速度迅速减小到零，啮合套与啮合齿轮之间的角速度差由Δω1减小到Δω2。本文假设在撞击过程中啮合套的轴向位移忽略不计［6］。

齿面撞击过程中，啮合齿轮和啮合套的角加速度如式6所示：

其中，μ2啮合齿轮花键齿端面与啮合套花键齿端面间摩擦系数；r2花键齿端面平均半径；Fimp齿面撞击时花键齿间的冲击力；β花键齿端面倒角。

由于齿面撞击持续时间t2－t1≈0，则根据动量定理可知在撞击过程中有式7成立：

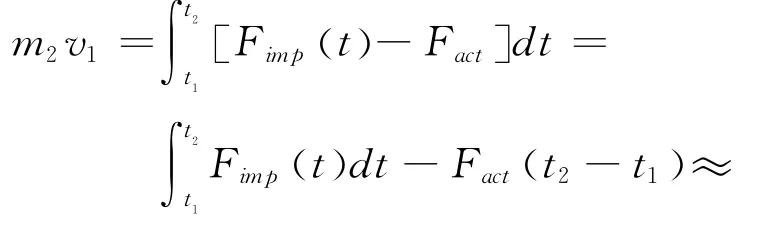
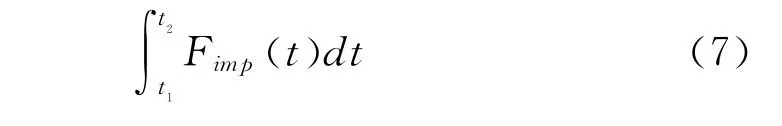
根据式6、7可以推导出啮合齿轮花键与啮合套花键撞击后二者间的角速度差的变化量Δωimp可表示为：

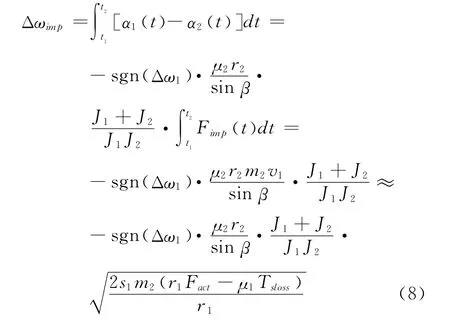
则t2时刻啮合齿轮与啮合套间的角速度差Δω2为：

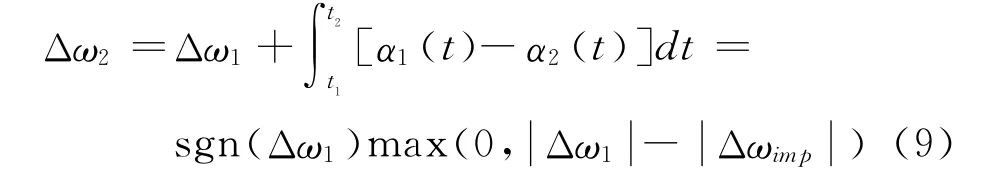
啮合齿轮花键与啮合套花键撞击前后二者的接触位置沿圆周的相对变化量的绝对值可以表示为：

其中，m2啮合套质量，v1初始滑行阶段结束时啮合套轴向速度。

由式10可知，在齿面撞击过程中因齿面间的冲击力而导致的啮合齿轮花键与啮合套花键相对位置的变化量可以忽略。但由式7可以知道，在齿面撞击过程中啮合齿轮与啮合套间的角速度差的变化量Δωimp的变化不能忽略不计。若，则啮合齿轮与啮合套角速度在齿面撞击阶段就可以达到同步。

2.1.3 齿面摩擦阶段

当啮合套的轴向速度稳定在零时，认为啮合套花键齿端面与啮合齿轮花键齿端面接触，齿面摩擦阶段开始，此时端面间的重叠量为φfstart；当啮合套与啮合齿轮角速度达到同步或啮合齿轮花键端面与啮合套花键端面脱离接触时该阶段结束，此时端面间的重叠量为φfend。

假设在t3时刻啮合套花与啮合齿轮角速度达到同步，则在该阶段啮合齿轮和啮合套的角加速度和角速度分别如式11、12所示：

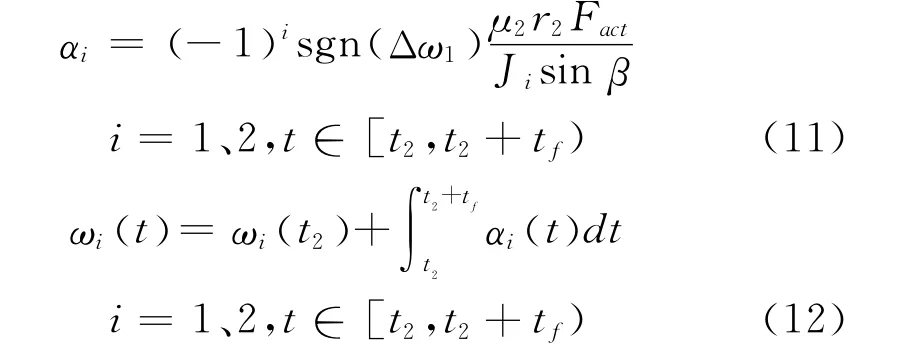
令式12中ω1（ t3）＝ω2（ t3），则由式1、2、3、9、11可知该阶段持续的时间为：

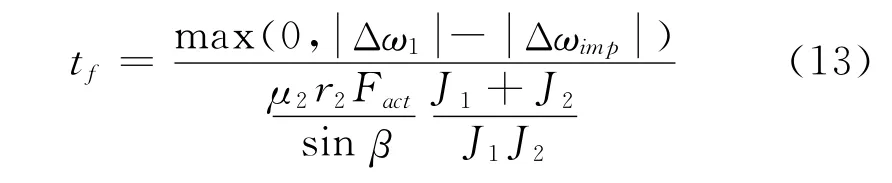
由式9、11、12和13可知，在tf时间内啮合齿轮花键与啮合套花键接触位置沿周向的相对改变量为：

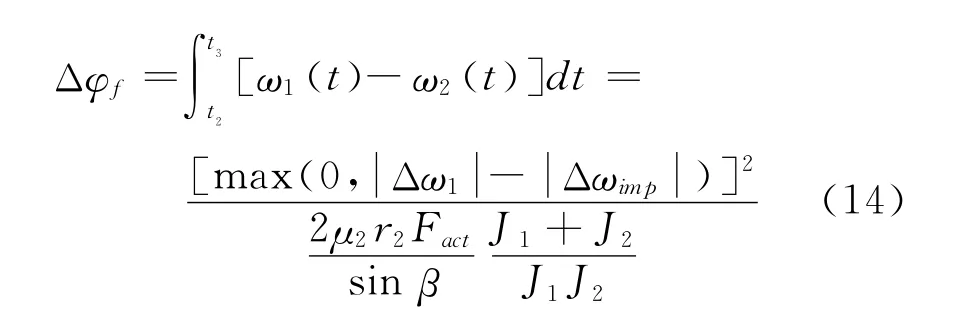
齿面摩擦阶段结束时，会有3种可能的情况出现：1）Δω3＝0，φfend≠0；2）Δω3＝0，φfend＝0；3）Δω3≠0，φfend＝0。第一种情况表示啮合齿轮与啮合套在齿面摩擦阶段转速达到同步，但花键齿端面将永久接触，啮合齿轮花键与啮合套花键不能相互啮合，自同步牙嵌式离合器换档啮合失败，如图3所示。第二和第三种情况表示齿面摩擦阶段结束时，啮合套花键齿端面与啮合齿轮花键齿端面间的重叠已经消除，此时不论相对速差Δω3是否为零，均能保证换档成功。

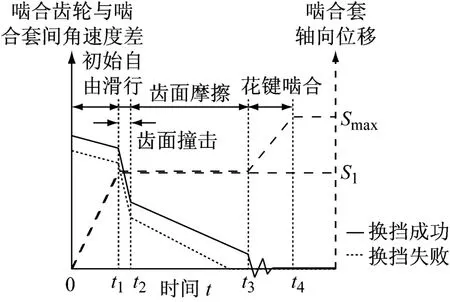
图3 自同步牙嵌式离合器换档成功和换档失败示意图Fig.3 Diagram of the self-synchronized jaw clutch shifting successfully and unsuccessfully

2.1.4 花键啮合阶段

这一阶段中啮合套沿轴向的受力情况与初始滑行阶段相同。在花键齿的啮合过程中，转速差Δω3会由于啮合齿轮花键与啮合套花键之间的撞击迅速减小至零，并会造成传动链短暂的扭转振动，其峰值为：

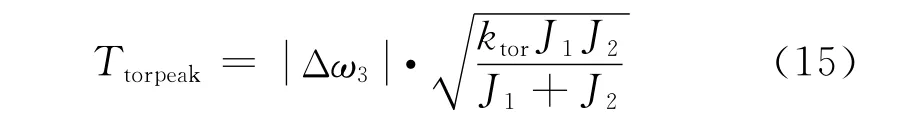
其中，Ttorpeak最后滑行阶段扭转振动峰值扭矩；ktor花键齿端面接触刚度。

2.2 自同步牙嵌式离合器换档啮合概率建模

由2.1.2可知，齿面撞击对啮合齿轮花键与啮合套花键相对周向位置的改变可以忽略，因此齿面摩擦阶段开始时啮合齿轮花键齿端面与啮合套花键齿端面间的重叠量φfstart决定了要成功完成换档啮合齿轮需要相对啮合套转动的角度。

由于φfstart是一个均匀分布的随机变量，本文引入随机因子ξ计算φfstart的大小，如图4所示。ξ在［0，2π／n］上服从均匀分布。

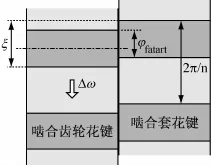
图4 啮合齿轮花键与啮合套花键相对位置Fig.4 The relative position of meshing gear spline and engaging sleeve spline

则齿面摩擦开始时端面重叠量φfstart可以用ξ表示为：

自同步牙嵌式离合器成功完成换档啮合的条件可以用下式表示：

本文中将某一换档速差下自同步牙嵌式离合器成功完成换档的概率定义为该换档速差下的换档容积。其表达式为：

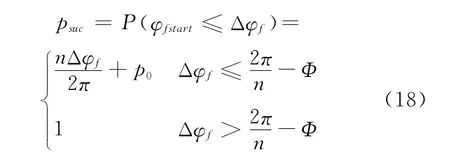
其中p0表示啮合齿轮花键与啮合套花键不发生接触而直接啮合的概率，其值可以表达为：

则由式14、16、17可知：

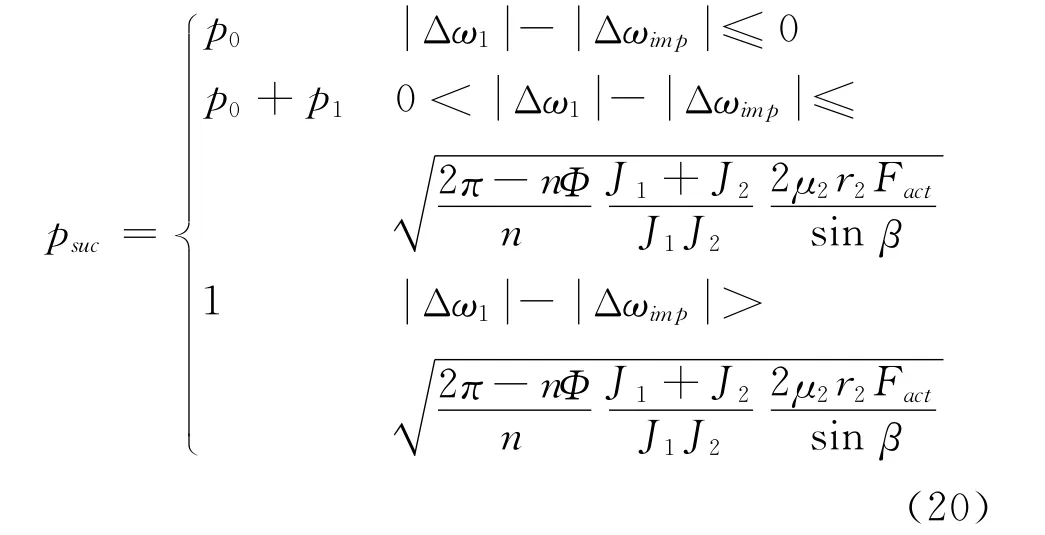
其中，p1为：

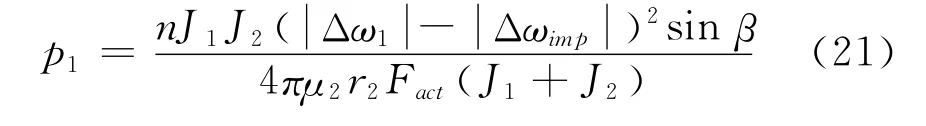
由于φfstar是一个随机变量，所以Δω3也是一个变量，其大小由φfstar与Δω0共同决定。

3 仿真分析及最佳换档速差的确定

利用Matlab／Simulink搭建自同步牙嵌式离合器动力学模型及其换档容积模型，采用变步长的ode23tb（TR-BFF2）求解器，相对误差设置为10－9。为加快模型的仿真速度，本文中用非线性的Sigmoid函数代替模型中的符号判断函数sgn（x），即

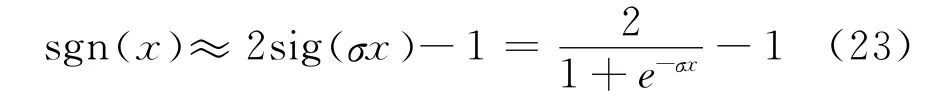
其中，σ为Sigmoid函数的平滑系数。

本文所研究的纯电动客车的1档、2档和3档在各个速差下的换档容积的仿真如图5和图6所示。

由图5可知，自同步牙嵌式离合器换档成功的概率psuc与Δω1是一个非线性变化的关系，随着｜Δω1｜的增加而逐渐增大，当｜Δω1｜增加到某一临界值后，psuc维持在其最大值1不再变化，且psuc关于Δω1＝0对称。齿面摩擦阶段开始时啮合齿轮与啮合齿套角速度差｜Δω1｜越大，齿面摩擦阶段啮合套花键齿端面与啮合齿轮花键齿端面沿圆周的相对位移就越大，齿面摩擦阶段结束时，啮合套花键齿端面与啮合齿轮花键齿端面间的重叠完全消除的可能性就大，从而导致换档成功的概率增加。但当｜Δω1｜增加到临界值时，齿面摩擦阶段结束时啮合套花键齿端面与啮合齿轮花键齿端面间的重叠已经完全消除，不论｜Δω1｜再如何增加，已不能影响此时的换档成功概率。

图5 换档成功概率与速差Δω1的关系曲线Fig.5 The relationship between the probability of successful engagement and speed difference（Δω1）

图6 换档成功概率与速差Δω1的关系曲线Fig.6 The relationship between the probability of successful engagement and speed difference（Δω0）

在相同Δω1下，各档位换档成功的概率并不相同，这是因为该概率不仅与各档位传动系统的转动惯量有关，还受各档位速比的影响。

在初始自由滑动阶段，可以认为啮合齿轮与啮合套均是减速转动。图6中的曲线相对图5中的曲线的移动取决于该阶段啮合齿轮角加速度变化量的绝对值与啮合套角速度变化量的绝对值之间的大小关系：1）若，则图6中的曲线相对图5中的曲线应是向右移动的；2）若，则图6中的曲线相对图5中的曲线应是向左移动的，本文中的情况属于后者。

图6中psuc刚达到1时的啮合齿轮与啮合套角速度差Δω0就是最佳换档速差Δω0opt。因为在这个速差下，不仅可以保证自同步牙嵌式离合器换档啮合成功，而且可以最大程度减小花键啮合阶段因残余速差Δω3造成的扭转振动。Δω0opt的数学模型为：

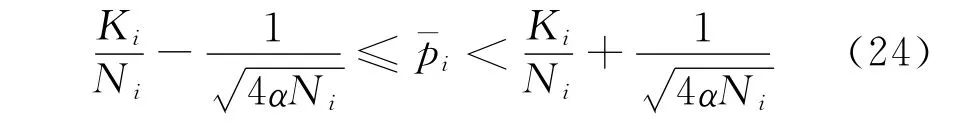
图7为换入3档时花键啮合阶段开始时啮合齿轮与啮合套之间的角速度差Δω3、需要转动的相对角度Δφfstart随啮合齿轮花键与啮合套花键相对位置ξ变化而变化的曲线。

图7 Δω3、Δφfstart与相对位置ξ的关系曲线Fig.7 The relationship betweenΔω3、Δφfstartandξ

4 试验验证

为验证本文对自同步牙嵌式离合器换档容积分析的正确性，通过台架试验对各档位在不同换档速差下的换档结果进行统计分析。啮合齿轮花键与啮合套花键端面开始碰撞时的转速差Δω1通过安装在变速器输入轴和输出轴上的转速传感器计算得到。表1为1档的实验结果，其中的数据包括Δω1区间、总共换档次数（N）、换档成功次数（K）和换档成功的频率（K／N）。

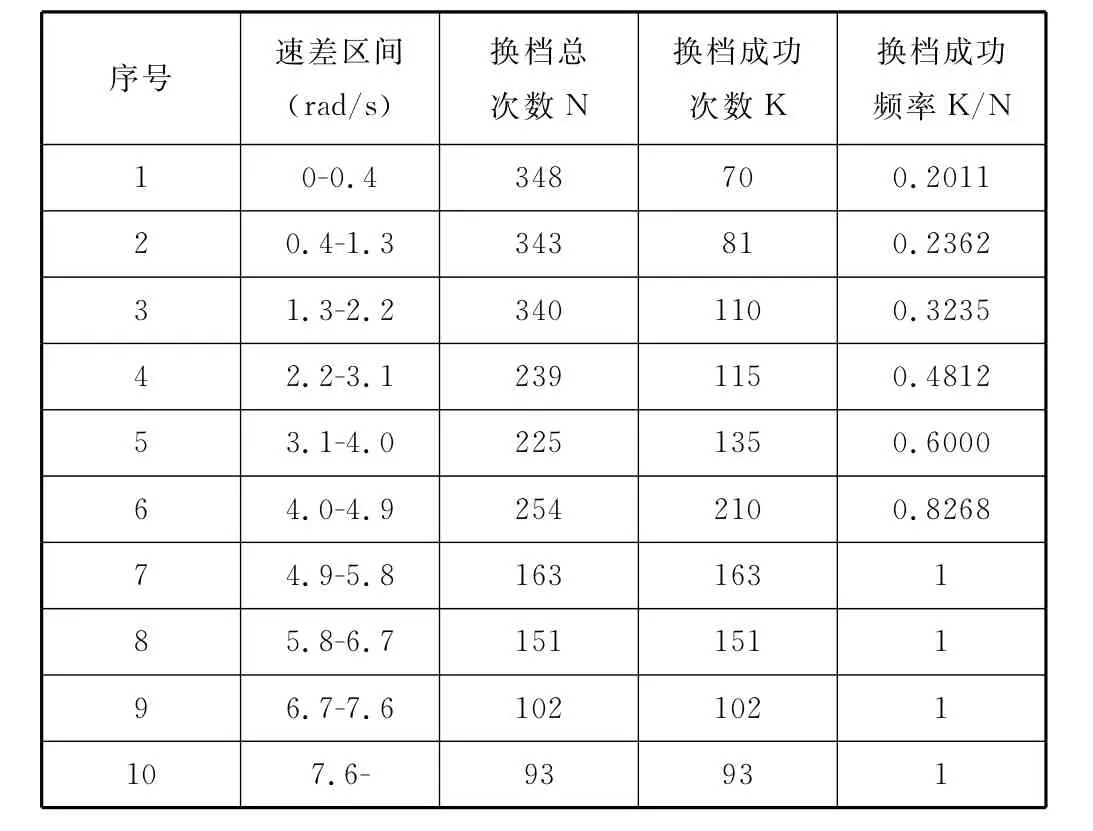
表1 1档试验数据Table 1 1st Test Data

每个Δω1区间上换档成功的概率区间可根据大数定律计算出来［7］，其表达式为：其中α取0.1，则上述估计的置信度为1－α＝0.9。

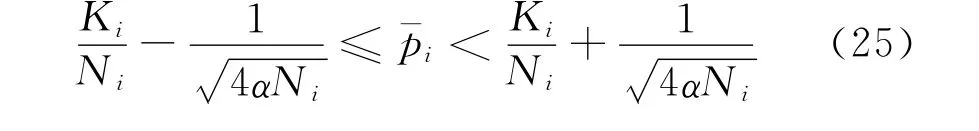
将1挡仿真数据、试验数据及置信区间画在同一幅图上，如图8所示。其中仿真数据即为本文通过上述理论仿真得到的1挡换档成功的概率，试验数据为各Δω1区间内1挡换档成功的频率（K／N），置信区间则为以试验数据为依据通过大数定律估计出来的每个Δω1区间上换档成功的概率范围。

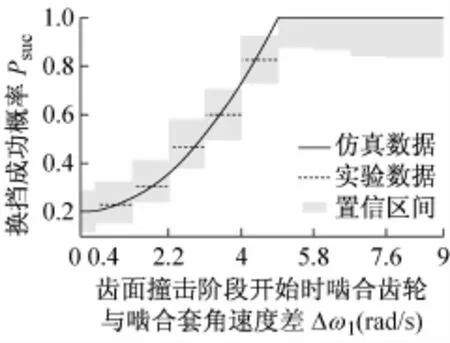
图8 1档试验数据与仿真数据比较及其置信区间Fig.8 Experimental results，simulation data and confidence interval of the first gear

通过分析图8可知，试验数据与仿真数据吻合，且通过实验数据计算出的各Δω1区间内1档换档成功的频率（K／N）都在置信区间范围内。这证明了本文对自同步牙嵌式离合器啮合机理的理论分析及其啮合成功概率模型的正确性和准确性。

5 结论

（1）自同步牙嵌式离合器换档啮合结果具有不确定性，这种不确定性受档位速比、该档位下传动系统转动惯量以及换档开始时的初始角速度差等诸多因素的影响。

（2）自同步牙嵌式离合器换档啮合成功的概率有一个确定的最小值。该值由牙嵌式离合器花键完全啮合后的尺侧间隙角决定，表征了自同步牙嵌式离合器换档啮合过程中不经过齿面撞击和齿面摩擦阶段而直接啮合的可能性。

（3）自同步牙嵌式离合器换档啮合成功的概率与初始角速度差是非线性变化的关系。该概率随着角速度差的增大而增大，但当角速度差达到某一临界值时，该概率达到最大值1，且不再随着角速度差的增大而变化。

（4）最优换档速差不仅可以保证自同步牙嵌式离合器换档啮合的成功，还可以最大程度减小花键啮合阶段因残余速差造成的扭转振动。

［1］ Lovas L，Play D，Márialigeti J，Rigal J F.Mechanical behavior simulation for synchromesh mechanism improvements［J］.Proc.Instn Mech.Engrs，Part D：J Automobile Engineering，2006.

［2］ Markus Schnabler.EV和HEV的爪形离合器变速器［J］.汽车零部件，2012（10）：26.Markus Schnabler.Transmission with dog clutches for EV and HEV［J］.Automobile Parts，2012（10）：26.（in Chinese）

［3］ 张 煜.纯电动客车自动变速系统及控制策略研究［D］.长春.吉林大学，2012.Zhang Yu.Research on Control Strategy of Automated Transmission System for Pure Electric Bus［D］.Changchun：Jilin University，2012.（in Chinese）

［4］ Laird M P B，Lawton B，Gregory R P.Dog clutches for rapid gear changes in automotive gearboxes［J］.Proceedings of the Institution of Mechanical Engineers，First International Conference，Gearbox Noise and Vibrations，IMech E，1990，pp.103-112.

［5］ Boness，R.J.Churning losses of discs and gears running partially submerged in oil［J］.Proceedings of the 1989 International Power Transmission and Gearing Conference，Chicago，pp.355-359.

［6］ Kim，J.，Sung，D.etc.Development of shift feeling simulator for a manual transmission［J］.SAE paper 2002-01-2202，2002.

［7］ Dougherty，E.R.Probability and statistics for the engineering，computing，and physical sciences，Prentice-Hall，Inc.，Upper Saddle River，NJ，USA，1990.

Engagement Mechanism Modeling and Successful Engagement Probability Analysis of Self-synchronized Jaw Clutch

Li Xingzhong1，2Song Bin1Tong Yanhua1Guo Lili1Lei Yulong2
（1.Hangzhou Advance Gearbox Group Co.，Ltd.，Hangzhou 311203；2.State Key Laboratory of automotive simulation and Control，Jilin University，Changchun 130022）

A dynamic model of a self-synchronized jaw clutch is established based on the analyses of its engagement process，and then the non-deterministic outcomes of the engagement process are described in the context of probability theory，and a model on calculating probability of the successful engagement is established accordingly.Afterwards，the factors that influence the probability of successful engagement during the gear shift process are studied through Matlab／Simulink simulation，and the optimal speed differences of the jaw clutch during different gear shifts are defined.Finally，simulation results are validated through a series of measurements on the test bench.An analytic results can be used for formulating the shift process control strategies of the self-synchronized jaw clutch as well as for optimizing the shift quality of the gearboxes with such clutches.

Vehicle engineering Self-synchronization jaw clutch Modeling Probability Torsional vibration

U463.11＋

A

1006-8244（2015）04-021-06

浙江省博士后科研项目择优资助项目（BSH1502066）