架空送电线路对地及交叉跨越距离的测量

余启育

（广东电网有限责任公司江门台山供电局，广东 江门529200）

0 引言

国家能源局DL／T741—2010《架空输电线路运行规程》对于架空送电线路的导线对地面、河流的距离以及对电力线路、弱电线（指电话线、有线电视、光缆等通信线）、铁路、公路、地上／地下构筑物的交叉跨越距离均作了具体规定，但随着架空送电线路的长期运行，下列原因会导致对地及交叉跨越距离发生变化：（1）在线路下面或其附近实施新建或改建工程，如道路、填土、电信线路或低压线路等。（2）由于改造工作移动了杆塔或改变了杆塔的尺寸、绝缘子串的长度。（3）导线松了而未调整或导线经过长时运行而拉长。（4）由于相邻两档内荷重不均匀，导线在悬垂线夹内滑动。

当架空送电线路的导线对地和交叉跨越距离发生变动时均需重新测量，测量方法有用绝缘测绳、绝缘测高杆直接测量和用全站仪间接测量。绝缘测绳、绝缘测高杆使用较简单，但受地形条件和测量尺长度限制大。下面主要针对全站仪测量方法展开探讨。

1 常规测量法

当目标点P的下方可以放置反光棱镜时，利用全站仪的悬高测量功能可以测出空中目标距地面点的高度，测量原理如图1所示。

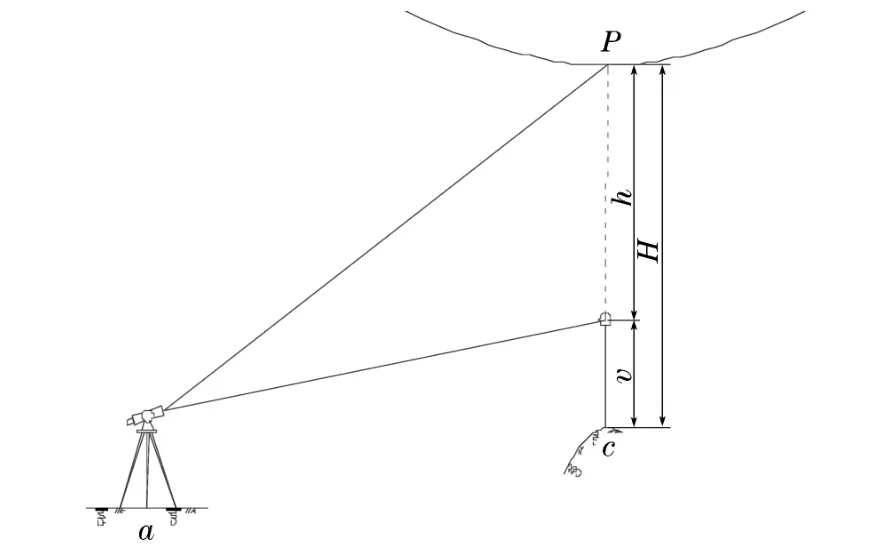
图1 悬高测量原理图

（1）将全站仪架设在距离测量对象较远处a点，使得测站望远镜到目标点P的垂直角度小于45°。因为垂直角较大的话，三角函数推算出来的高差误差较大。（2）在目标点P投影到地面上的基准点架起棱镜。测站和地面基准点的连线，最好与送电线路走向垂直相交。（3）进入全站仪的悬高测量程序，输入棱镜高度v，瞄准棱镜并按测量键，测出测站与棱镜的距离。（4）松开望远镜垂直方向的制动，照准棱镜上方的目标点P，全站仪会随着垂直度盘的转动，实时显示出对应的目标点P到地面的高差H。

由上述步骤可见，当目标点下方可以放置反光棱镜时，利用全站仪来进行悬高测量很方便。值得注意的是，要想利用悬高测量功能测出目标点的正确高度，必须将反射棱镜恰好安置在被测目标点的投影点，否则测出的结果将是不正确的。

2 单向测量法

当目标点下方为河流、湖泊、山谷等无法放置反光棱镜的地形时，从图2中可以看出，当反光棱镜安置的位置偏离P点的投影点d而放置至c点时，用全站仪进行悬高测量得出的数值实际上是点P′距地面的“视悬高”H′，也就是说反光棱镜只要偏离被测目标的铅垂线，全站仪就无法得到正确的结果。c点和d点相差的距离越大，“视悬高”H′和真正的悬高H 的误差也就越大。

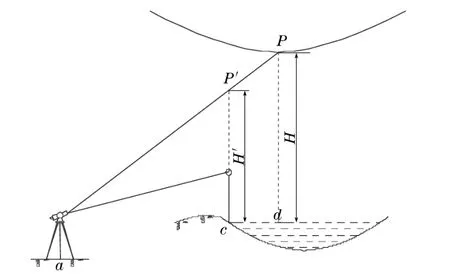
图2 反光棱镜偏离目标示意图

这种特殊情况下既没有办法安置棱镜，又得不到其投影点，此时可以使用单向测量法，测量原理如图3所示。

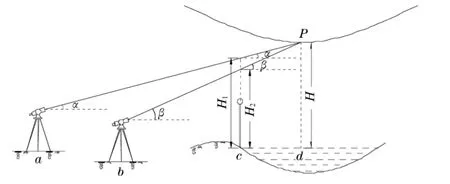
图3 单向测量法悬高测量原理图

（1）在远离目标的a点处安置全站仪，在aP方向线上适当位置c点安置反射棱镜，用全站仪的悬高测量功能测出P点的“视悬高”H1和P点的竖直角α，那么此时真正的悬高H为：

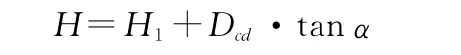
式中，Dcd为棱镜安置点至P点的水平距离，为未知数。

（2）接着在aP方向线上适当位置b点安置全站仪，安置反射棱镜位置不变（c点），用全站仪的悬高测量功能测出P点的“视悬高”H2和P点的竖直角β，那么此时真正的悬高H为：

（3）根据以上两式消去Dcd可得出真正的悬高H 公式：

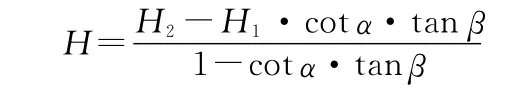
将以上测出的“视悬高”H1、H2和竖直角α、β代入上式，即可求得真正的悬高H。

3 三角函数法

单向测量法在测定单个目标时比较好用，但当某一相导线因为松弛需对这相导线上多个目标点进行测定时，由于单向测量法每测定一个点都需设置2个测站，测量工作量很大。利用方位交汇法，可以测量线路上的固定点和待测目标点的坐标，通过测设的方法确定出待测点的投影位置，然后运用三角函数计算的方法得出结果。如图4所示，b、c两点为电力线路导线的固定点，P 为线路上的目标点，a为全站仪测站 点，a′、b′、c′、P′为这几点在水平面上的投影点。利用正弦、余弦三角函数法，可以计算出测站点a至目标点P的水平距离和悬高H。

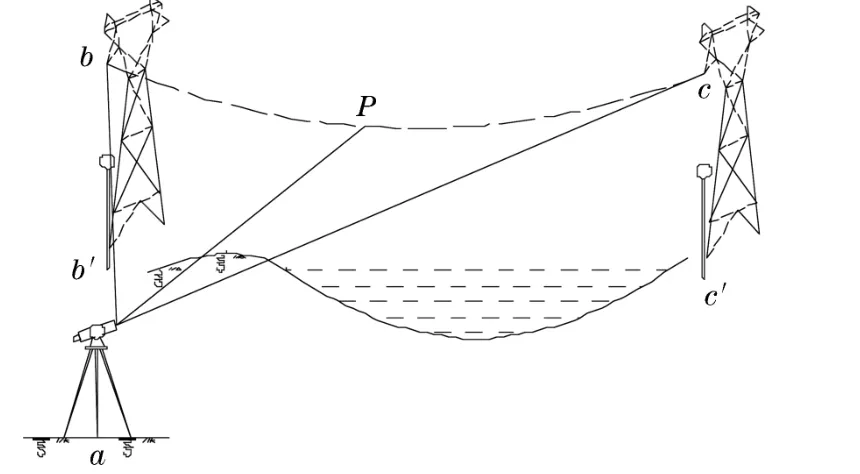
图4 三角函数法悬高测量原理图

（1）在远离目标的a点处安置全站仪，在导线的固定点b下方投影点安置反射棱镜，并将此方向角度置零，测出测站a与棱镜b的水平距离Da′b′。投影图如图5所示。

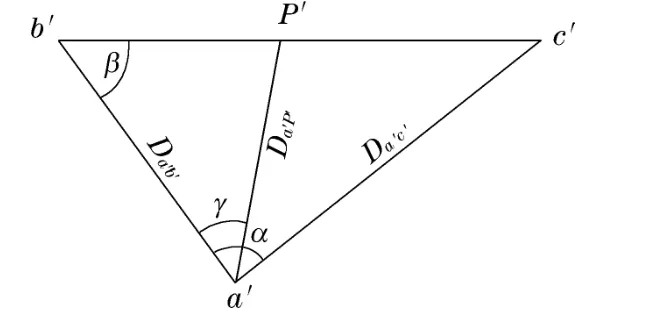
图5 三角函数法水平投影图

（2）在导线的固定点c点下方投影点安置反射棱镜，测出测站a与棱镜c的水平距离Da′c′和∠bac的水平夹角α。

（3）根据余弦定理计算出导线的固定点b、c的水平距离为：

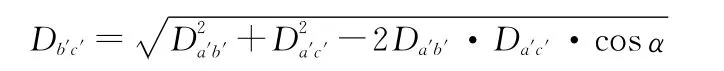
式中，Da′b′为a点至b点的水平距离；Da′c′为a点至c点的水平距离。

（5）转动全站仪，照准导线上的任意目标点P，测出∠baP的水平夹角γ和垂直夹角θ，根据正弦定理有

（6）目标点P的高程：HP＝测站高程＋仪器高＋Da′P′·tanθ。

（7）再用全站仪测出水面的高程后，用目标点P的高程减去水面的高程即可得出导线悬高H。

4 双站三角函数法

本方法主要是对三角函数法的一个补充完善，如图6所示，当由于地形和通视问题限制无法在固定点b、c下方投影点安置反射棱镜时，可以采用双站三角函数法的方法进行悬高测量。利用双站三角函数法，通过多增加一个测站d，可以计算出测站a到导线的固定点b、c的水平距离，再通过三角函数法来进行悬高测量。

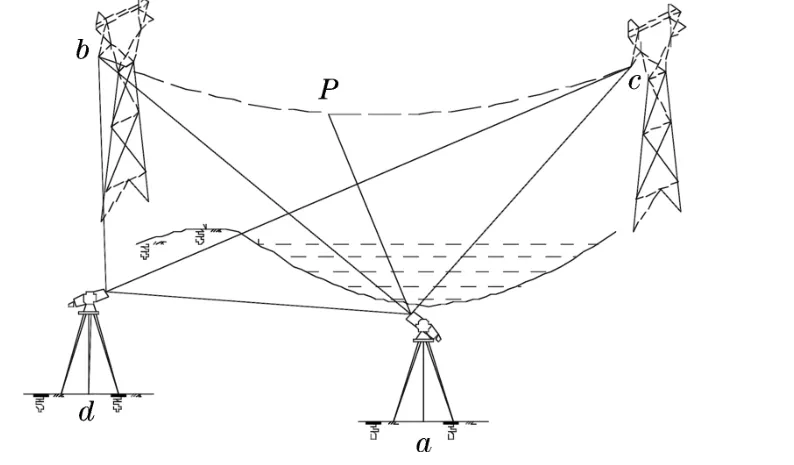
图6 双站三角函数法悬高测量原理图

（1）以三角函数法为基础，在合适的位置增设测站点d，在d点安置全站仪，在测站点a安置反射棱镜，测出测站d与棱镜a的水平距离Da′d′和∠bda的水平夹角d1、∠cda的水平夹角d2。投影图如图7所示。

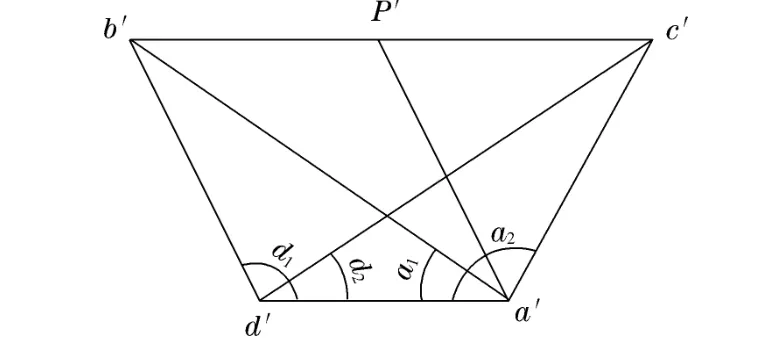
图7 双站三角函数法水平投影图

（2）在测站点a安置全站仪，测出∠dab的水平夹角a1、∠dac的水平夹角a2。

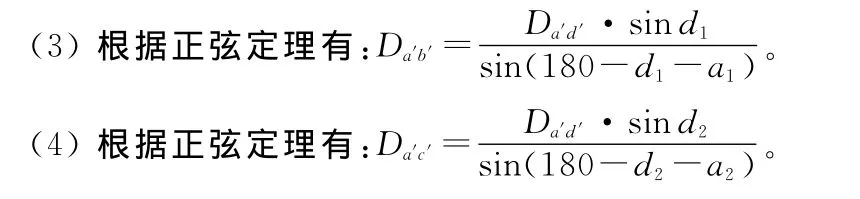
（5）求出 Da′b′、Da′c′后，可按三角函数法的第（3）～（7）步来测出目标点P的悬高。

为提高测量精度，在选定测站时，应注意2个测站的间隔不宜太近，以防在计算过程中由于四舍五入而产生新的误差。

5 结语

利用全站仪来测量架空送电线路对地及交叉跨越距离是一种方便、快捷、精确的作业手段，本文所述方法中，常规测量法简单快捷，单向测量法可以有效解决投影点处无法安置反光棱镜的问题；三角函数法及双站三角函数法可以对导线上多个目标点进行测定，以有效地解决文中所述的问题，从而得到被测目标点的精确对地及交叉跨越距离。

［1］唐云岩.送电线路测量［M］.中国电力出版社，2004

［2］陈久强，刘文生.土木工程测量［M］.第2版.北京大学出版社，2012