广义量词的现代对当方阵研究
2015-03-14林胜强
林 胜 强
(四川师范大学政治教育学院,成都610066)
广义量词的现代对当方阵研究
林 胜 强
(四川师范大学政治教育学院,成都610066)
在现代对当方阵中,逻辑规律具有一致性。对一个现代对当方阵中的任意一个广义量词施加任意多次的三种形式的否定运算,得到的广义量词仍然是原来的现代对当方阵中的广义量词。在〈1,1〉类型的广义量词所对应的现代对当方阵中,不但广义量词与其三个否定量词的单调性之间具有可转换关系;而且它们所对应的广义三段论之间具有可化归关系。由于〈1,1〉类型广义量词在自然语言中普遍存在,所以,此研究对计算机科学中的知识表示和知识推理具有重要的意义。
广义量词;对当方阵;单调性;广义三段论
20世纪中期,人们发现:(1)自然语言中存在很多不能够用一阶逻辑中的标准量词∀和∃来加以定义的,但却具有非常有趣的数学推理性质的量词[1];(2)自然语言中还存在亚里斯多德三段论以外的大量有效推理[2],这些推理就是基于广义量词的扩展三段论的推理。这孕育了广义量词理论(generalized quantifier theory)的诞生。广义量词包括:(1)一阶逻辑的全称量词和存在量词;(2)限定词;(3)由限定词a,an,the或其他量化关系所组成的所有名词短语。在这里,限定词是指能够修饰名词的语词,比如:这个、那个、红色的、至少三分之二的,四个,等等。20世纪80年代以来,在Barwise和Cooper[3]、 Keenan[4]、 Van Eijck[5]、 Peters 和Westerståhl[6]、Szymanik[7]、Chow Ka Fat[8]等人工作的基础上,广义量词理论得到了大力发展。广义量词理论的表达力就于一阶逻辑的表达力。
广义量词理论以集合论为基础,通过模型论对广义量词进行形式化的解释,其基本思想就是:根据广义量词的论元所涉及的集合的性质,或者集合之间的关系来解释广义量词的普遍语义特征[9]。广义量词理论处理问题的方式直观简洁,其成果普适性很强,便于对自然语言的信息处理,其研究成果对于逻辑学、理论语言学、计算语言学、计算机科学等交叉领域都有着重要的意义。在本文中:用A、B、C表示广义量词所涉及的论元所组成的集合,用E、F表示所讨论的论域;广义量词用其对应的英语来表示;若无特别说明,量词都是指广义量词。
需要特别说明的是,广义量词理论和本文中研究的“量词”都是指“广义量词”,它们与汉语语言学中的“量词”是完全不同的两个概念。按张晓君的观点:大致说来,汉语语言学家认为的“表示事物或动作单位”的“量词”与数词、指代词组成的量词短语,就相当于英语语言中指称名词短语中的量化词项的“限定词”;对汉语语言中的量词短语或名词短语进行语义解释后就得到了集合论中的广义量词,汉语中的“专有名词”,如张三、李四也是广义量词。自然语言中的限定性词语和已经名词化的词语也是广义量词,自然语言中的一些副词性词语,比如:“常常、经常、很少、有时、从不”也是广义量词[10]。
一 问题的提出
在自然语言中,最为普遍存在的是〈1〉类型量词和〈1,1〉类型量词。〈1〉类型量词表示其论元所组成集合的性质,常见名词短语对应〈1〉类型量词。〈1,1〉类型量词表示广义量词左论元和右论元所涉及的集合之间的二元关系,绝大多数限定词对应〈1,1〉类型量词。对〈1〉类型量词的研究常常可以转化为对其〈1,1〉类型的亲缘量词的研究,因而本文重点研究〈1,1〉类型量词。比如“最多五分之一的少年有网瘾”这一语句中的名词短语“最多五分之一的少年”就是〈1〉类型量词,该量词表示“最多五分之一的少年”组成的集合具有“有网瘾”的性质。而这一语句中的限定词“最多五分之一的”就是〈1,1〉类型量词,“最多五分之一的”就是“最多五分之一的少年”的亲缘量词。在自然语言中,任何含有〈1,1〉类型量词Q的量化语句都可以表示为Q(A,B)这样的三分结构,其中A表示量词左论元所组成的集合,B表示量词的右论元所组成的集合。比如“最多五分之一的少年有网瘾”可用Q(A,B)表示,其中“最多五分之一的”对应的是〈1,1〉类型量词Q,A表示论域中所有的少年组成的集合,B表示有网瘾的少年组成的集合。在广义量词理论中,“最多五分之一的”的真值定义是:(at most 1/5 of the)E(A,B)⇔|A∩B|≤1/5|A|,这里的E表示论域,即“最多五分之一的”的语义就是通过“A与B交集的基数小于或等于A的基数的五分之一”来刻画的。类似地,语句“所有的人都渴望得到幸福”可以表示为all(A,B),量词“所有的”的真值定义是all(A,B)⇔A⊆B。
如果一个量词在某个论域上的任意关系是全关系(universal relation),这种量词叫作全量词,我们用粗体1来表示。如果一个量词在某个论域上的任意关系是空关系(empty relation)时,这种量词叫做空量词,我们用粗体0来表示。这两种量词是非足道(trivial)量词,其他量词则是足道(non-trivial)量词。广义量词的主要性质有:同构闭包性、扩展性、驻留性、单调性、对称性、相交性等等。单调性则是广义量词最重要的语义性质。由于〈1,1〉类型量词有两个论元,故其单调性有左右之分。下面定义1中前四种单调性是广义量词的基本单调性,后四种单调性叫做斜向单调性。
定义1[11]47-52:令Q是一个〈1,1〉类型量词,对任意集合A、B、C和论域E、F而言:
(1)Q是右单调递增的(记作Mon↑),当且仅当:若 B⊆C⊆E,则 QE(A,B)⇒QE(A,C);
(2)Q是右单调递减的(记作Mon↓),当且仅当:若 B⊆C⊆E,则 QE(A,C)⇒QE(A,B);
(3)Q是左单调递增的(记作↑Mon),当且仅当:若B⊆C⊆E,则QE(B,A)⇒QE(C,A);
(4)Q是左单调递减的(记作↓Mon),当且仅当:若B⊆C⊆E,则QE(C,A)⇒QE(B,A)。
(5)QE是东南方向单调递增的(记作↑SEMon),当且仅当:若QE(B,A)且B⊆C⊆E且B-A=C-A,则QE(C,A);
(6)QE是西南方向单调递增的(记作↑SWMon),当且仅当:若QE(B,A)且B⊆C⊆E且B∩A=C∩A,则QE(C,A);
(7)QE是西北方向单调递减的(记作↓NWMon),当且仅当:若QE(C,A)且B⊆C⊆E且B -A=C-A,则QE(B,A);
(8)QE是东北方向单调递减的(记作↓NEMon),当且仅当:若QE(C,A)且B⊆C⊆E且B∩A=C∩A,则QE(B,A)。
二 古典对当方阵与现代对当方阵之异同
早在2300多年前,亚里斯多德就对all、some、no、not all这四个亚氏量词有所研究。亚氏三段论可以看作是这四个〈1,1〉类型量词的推理性质的形式化解释。一个三段论具有这样的形式:

在亚里斯多德工作的基础上,大家认为:一个有效的三段论可以有假前提,如若前提真而结论假,那么该三段论就是无效的,否则,就是有效的三段论。后来,一些学者使用对角线的形式把这些亚氏量词表示在古典对当方阵中(见下页图1)。
19世纪末以来,一些学者发现古典对当方阵所描述的逻辑规律有冲突的地方[12]。例如,no(A,B)不能蕴涵现代对当方阵(见下页图2)中的not all(A,B),这是因为在现代对当方阵中,all没有假定主项一定存在,而not all则假定了主项一定存在。但是 no(A,B)确实蕴涵古典意义的 not allei(A,B),这是因为在古典对当方阵中,allei假定了主项一定存在,而not allei没有假定主项一定存在。这一假定与现代对当方阵正好相反[6]22-26。此外,古典对当方阵对指称空集的表达式的空词项的处理不够充分[13]220-224。然而,古典对当方阵对于像all、every这些词的解释,还是很大程度上达到了逻辑学和语言学的目的。从19世纪末以来,现代对当方阵规定量词all不假定主项一定存在,而not all则假定主项一定存在。基于以上这些原因,为了与现代对当方阵中的all与not all区分开来,我们在古典对当方阵中的all与not all都加上了下标ei。与古典对当方阵相比较,现代对当方阵的主要优点是:一是没有逻辑规律上的冲突,二是能够揭示出自然语言和逻辑语言中的三种重要的否定形式(即外否定、内否定、对偶否定)之间的相互关系[14]。
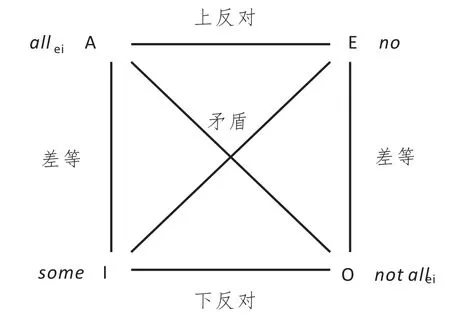
图1.古典对当方阵
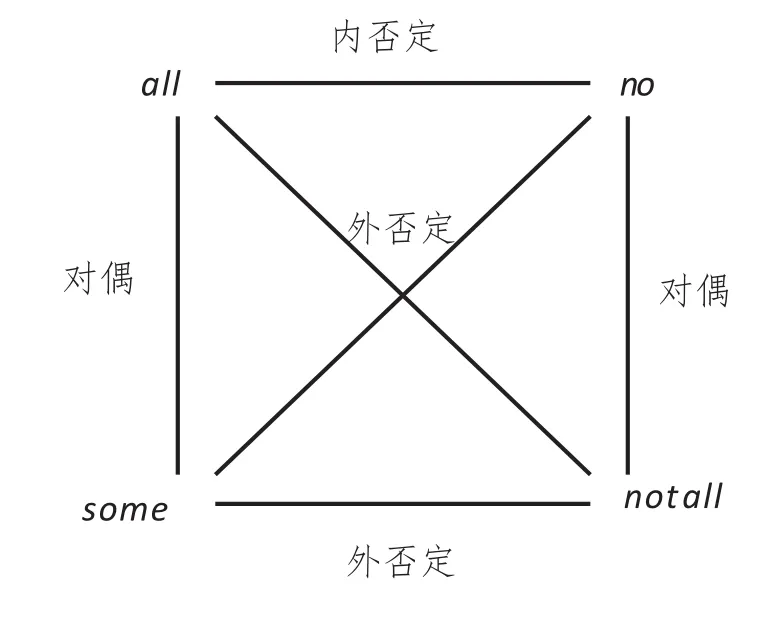
图2.现代对当方阵
在现代对当方阵中,对角线两端的量词互为外否定(outer negation)量词,水平线两端的量词互为内否定(inner negation)量词,铅垂直线两端的量词则互为对偶(dual)否定量词。对〈1,1〉类型广义量词Q而言,令¬Q表示其外否定量词、Q¬表示其内否定量词、Qd表示其对偶否定量词,则其三种否定量词的定义[6]92-93是:
定义2:〈1,1〉类型量词的三种否定运算:

Q的对偶否定就是Q的内否定的外否定,或Q的对偶否定就是Q的外否定的内否定。
三 广义量词的现代对当方阵研究
在之前论述的基础上,现在我们就可以给出广义量词的现代对当方阵的定义[6]133。
定义3:现代对当方阵:
对一个对〈1,1〉类型或〈1〉类型的广义量词Q而言,Q的对当方阵简记为square(Q),而且square(Q)= {Q,¬Q,Q¬,Qd}
例如,图2中的现代对当方阵可以记作square(all)= {all,not all,no,some}。每一个广义量词都可以生成一个现代对当方阵。例如:square(at most n)={at most n,more than n,all but at most n,less than n},其中的n为自然数。因为:at most n是〈1,1〉类型量词,令Q=at most n,根据定义2(1),得:(¬Q)E(A,B)⇔并非QE(A,B)⇔并非(at most n)(A,B)⇔more than n(A,B),所以,¬Q=more than n。根据定义2(2),得:(Q¬)E(A,B)⇔QE(A,E-B)⇔(at most n)(A,E-B)⇔(all but at most n)(A,B),所以 Q¬= all but at most n。根据定义 2(3),得:(Qd)E(A,B)⇔¬((Q¬)E(A,B))⇔¬(all but at most n)(A,B)⇔less than n(A,B),所以Qd=less than n。
在现代对当方阵中,对一个广义量词进行这三种形式的否定运算,其结果是封闭的。也就是说,对一个现代对当方阵中的任意一个广义量词施加任意多次的这三种形式的否定运算,得到的广义量词仍然是原来的现代对当方阵中的广义量词[6]24-26。例如:在现代对当方阵 square(all)中,¬¬¬(somed)¬¬=¬(somed)¬¬=¬(somed)=¬all=not all。
后来的学者研究表明,这三种形式的否定在自然语言中都是大量存在的,而且任意一个广义量词都可以产生一个现代对当方阵。这一点对古典对当方阵而言是不成立的,因为只有现代对当方阵中的量词的外否定在古典对当方阵中,而量词的其他两种形式的否定形式都不在古典对当方阵中。如果没有特殊说明,以下的对当方阵都是指现代对当方阵。对现代对当方阵而言,有如下事实成立:
事实 1[6]133-134:
(1)空量词0与全量词1所对应的对当方阵相同,即square(0)=square(1)={0,1};
(2)如果Q既不是空量词,也不是全量词,那么在Q的对当方阵中的其他三个否定量词也既不是空量词,也不是全量词;
(3)一个对当方阵中的每一个量词生成的对当方阵都是一样的。即:如果 Q′∈ square(Q),那么square(Q)=square(Q′)。
(4)任何一个对当方阵square(Q),要么有两个成员,要么有四个成员。
文献[6]仅仅给出了事实1的(2)(3)(4)的简略证明。在此,我们可以给出以下完整的证明。
(1)当Q是空量词时,即有Q=0,那么¬Q=¬0=1,Q¬=0¬=1-0=1,这时¬Q=Q¬=1;而Qd=¬(Q ¬)=¬1=0,这时 Q=Qd=0,所以 square(0)={0,1}。类似地,当Q是全量词时,即有Q=1,则¬Q=¬1=0,Q¬=1¬=1-1=0,这时¬Q=Q¬=0,而 Qd=¬(Q¬)=¬0=1,这时 Q=Qd=1,所以 square(1)={0,1}。故,square(0)=square(1)={0,1},即空量词0与全量词1所对应的对当方阵相同。
(2)假设Q既不是空量词,也不是全量词,那么就存在论域E,A、B⊆E,使得QE(A,B),而且存在E′,A′、B′⊆E′使得,并非QE′(A′,B′);这对于对当方阵中的其它量词也是一样的。例如,令B1=E-B,且B2=E′-B′,则QE(A,E-B1),并非QE′(A′,E′-B2),即(Q¬)E(A,B1),并非(Q¬)E′(A′,B2),因此Q¬也既不是空量词,也不是全量词。
(3)这里需要考虑(a)与(b)两种情况。(a)如果Q是非足道量词0或1,那么事实1(1)已经证明square(0)=square(1),故结论成立。(b)如果Q是足道量词。例如,我们可以证明 square(Q¬)=square(Qd)。 根据定义2有:¬(Q¬)=Qd,(Q¬)¬=Q,(Q¬)d=¬(Q¬)¬=¬Q,所以square(Q¬)={Q¬,Qd,Q,¬Q};再根据定义2有:¬(Qd)=¬(¬Q¬)¬=Q¬,(Qd)¬=(¬Q¬)¬=¬Q,(Qd)d=¬(¬Q¬)¬=Q,square(Qd)={Qd,Q¬,¬Q,Q},可见square(Q ¬)=square(Qd){Q¬,Qd,Q,¬Q}= square(Q)。其他情况证明与此类似。
(4)由于任意广义量词与它的外否定量词是不同的,因而在对当方阵中最少存在两个量词。现在只需要考虑(a)与(b)两种情况:(a)当¬Q≠Q¬时,Qd=¬Q¬,即Qd是Q¬的外否定,那么Qd≠Q¬,即此时Q≠¬Q≠Q¬≠Qd,这时对当方阵中就有四个成员。(b)当¬Q=Q¬时,Qd=¬Q¬=Q¬¬=Q,这时对当方阵就只有两个成员。根据(1)的证明可知,这种情况是存在的。因此,对当方阵中要么有两个成员,要么有四个成员。结论得证。
四 同一个对当方阵中的广义量词之间的关系
在文献[6][8]和[13-15]的基础上,张晓君发现:在同一个对当方阵中,不同广义量词的单调性之间有着密切的关系。例如:对〈1,1〉类型的广义量词而言,在同一个对当方阵中,不同广义量词的单调性之间具有可转换关系,即:互为外否定的两个量词的左右单调性完全相反;互为内否定的两个量词的左单调性相同,右单调性相反;互为对偶否定的两个量词的左单调性相反,右单调性相同。这一可转换关系可概括成“外否左右反,内否左同右反,对偶左反右同”[15]673-678。 例如,四个〈1,1〉类型的亚氏量词就存在这样的转换关系,请参见图3、图4。

图3.“all”的现代对当方阵中量词的单调性及其相互关系
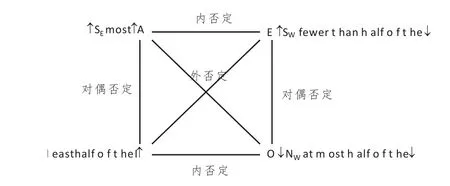
图4.“most”的现代对当方阵中量词的单调性及其相互关系
在图3中,↓all↑表示all是右单调递增且左单调递减的量词,其外否定量词not all的左右单调性正好与它相反,是右单调递减且左单调递增的,即:↑not all↓,其他与此类似。图4中的〈1,1〉类型量词“most”的基本单调性也满足这样的转换关系;而其斜向单调性之间也具有一定的转换关系,具体地说:互为外否定的量词的东与西、南与北、递增与递减正好相反;互为内否定的量词同增同减,只是东与西正好相反;互为对偶否定的量词也同增同减,只是南与北正好相反。
正如广义量词是亚氏量词的扩展一样,广义三段论是亚氏三段论的扩展,广义三段论是指涉及广义量词的三段论,也叫扩展三段论[16]。经过深入研究,我们发现:正是由于在同一个对当方阵中,不同广义量词的单调性之间具有可转换关系,决定了在同一个对当方阵中,不同广义量词所对应的有效广义三段论之间具有可化归关系。我们还是以自然语言中占绝大多数的〈1,1〉类型的广义量词为例。在此,笔者提出事实2,并给出其详细证明。
事实2:对一个〈1,1〉类型的广义量词Q而言,Q是右单调递增的,当且仅当all(B,C)&Q(A,B)⇒Q(A,C),当且仅当all(B,C)&¬Q(A,C)⇒¬Q(A,B),当且仅当all(B,C)&Q¬(A,C)⇒Q ¬(A,B),当且仅当 all(B,C)& Qd(A,B)⇒Qd(A,C)。
证明:先从左到右证明。此证明分(a)(b)(c)(d)四个步骤。(a)对一个〈1,1〉类型量词 Q而言,假设Q是右单调递增的,根据定义1(1)右单调递增的定义可知,对于任意的论域E和集合B与C,如果B⊆C⊆E,那么QE(A,B)⇒QE(A,C)。再根据广义量词理论给出的all的真值定义可知,对于任意的论域E,allE(B,C)⇔B⊆C⊆E。故,此时有:all(B,C)&Q(A,B)⇒Q(A,C)。(b)此时,继续假设语句all(B,C)成立,对Q(A,B)⇒Q(A,C)的两边取否定运算,可得:¬Q(A,C)⇒¬Q(A,B),此时就证明了 all(B,C)& ¬Q(A,C)⇒¬Q(A,B)。(c)又由于Q是右单调递增的,根据其定义可知,对所有的B⊆C⊆E,那么QE(A,B)⇒QE(A,C)。根据定义2(2)内否定的定义可知,(Q¬)E(A,C)⇔QE(A,E-C),(Q¬)E(A,B)⇔QE(A,E-B)。也就是说,内否定只对其右论元取补运算,对左论元没有影响,这就相当于仅仅对右论元取外否定运算,故由QE(A,B)⇒QE(A,C),可得QE(A,E-C)⇒QE(A,E-B),即Q¬(A,C)⇒Q¬(A,B),此时就证明了all(B,C)&Q¬(A,C)⇒Q¬(A,B)。(d)此时,继续假设语句all(B,C)成立,对Q¬(A,C)⇒Q¬(A,B)的两边取否定运算,可得:¬Q¬(A,B)⇒¬Q¬(A,C),再根据Qd=¬Q¬这一定义可知,Qd(A,B)⇒Qd(A,C),此时就证明了all(B,C)&Qd(A,B)⇒Qd(A,C)。反方向的证明与此类似。证毕。
例如,由于more than 2/3 of是右单调递增的量词,若令Q=more than 2/3 of,则¬Q=at most 2/3 of,Q¬=less than 1/3 of,Qd=at least 1/3 of,根据事实2可得:
推论1:more than 2/3 of是右单调递增的,当且仅当all(B,C)&more than 2/3 of(A,B)⇒more than 2/3 of(A,C),当且仅当 all(B,C)& at most 2/3 of(A,C)⇒at most 2/3 of(A,B),当且仅当all(B,C)&less than 1/3 of(A,C)⇒less than 1/3 of(A,B),当且仅当all(B,C)& at least 1/3 of(A,B)⇒at least 1/3 of(A,C)。
也就是说,这四个广义三段论都是有效推理,而且它们之间具有可化归关系。对此,我们举一个自然语言的例子来加以说明。例如,广义三段论实例[1]有效,当且仅当广义三段论实例[2]有效,当且仅当广义三段论实例[3]有效,当且仅当广义三段论实例[4]有效:
[1]前提1:所有渴望得到爱情的人都是心智健全的人。
前提2:超过三分之二的人都渴望得到爱情。
结 论:超过三分之二的人都是心智健全的人。
[2]前提1:所有渴望得到爱情的人都是心智健全的人。
前提2:最多三分之二的人是心智健全的人。
结 论:最多三分之二的人渴望得到爱情。
[3]前提1:所有渴望得到爱情的人都是心智健全的人。
前提2:不到三分之一的人是心智健全的人。
结 论:不到三分之一的人渴望得到爱情。
[4]前提1:所有渴望得到爱情的人都是心智健全的人。
前提2:最少三分之一的人渴望得到爱情。
结 论:最少三分之一的人是心智健全的人。
综上所述,广义量词的现代对当方阵具有逻辑一致性。对一个现代对当方阵中的任意一个广义量词施加任意多次的三种形式的否定运算,得到的广义量词仍然是原来的现代对当方阵中的广义量词。对自然语言中占绝大多数的〈1,1〉类型的广义量词而言,在同一个对当方阵中,不仅不同广义量词的单调性之间具有可转换关系,而且不同广义量词所对应的有效广义三段论之间具有可化归关系。由于广义量词理论进行自然语言信息处理的方式直观简洁,其研究成果有利于计算机的知识表示和知识推理,因此我们有必要加强研究。
[1]MOSTOWSKI A.On a Generalization of Quantifiers[J].Fund Math,1957,44:12-36.
[2]张晓君.扩展三段论的可化归性与广义量词的语义性质之间的关系[J].逻辑学研究,2012,(2):63-74.
[3]BARWISE J,COOPER R.Generalized Quantifiers and Natural Language[J].Linguistics and Philosophy,1981,(2):159-219.
[4]KEENAN E L.The Semantics of Determiners[C]//The Handbook of Contemporary Semantic Theory.Blackwell Publishing,1997.
[5]VAN EIJCK J.Syllogistics=Monotonicity+Symmetry+Existential Import[EB/OL].[2012-06-18].http://www.oai.cwi.nl/oai/asset/10940/10940D.pdf.2005.
[6]PETERS S,WESTERSTåHI D.Quantifiers in Language and Logic[M].Oxford:Claredon Press,2006.
[7]SZYMANIK J.Quantifiers in Time and Space[M].Polen:Geboren te Warschau,2009.
[8]Chow K F.Inferential Patterns of Generalized Quantifiers and their Applications to Scalar Reasoning[D].Hong Kong Polytechnic University,2012.
[9]张晓君.广义量词的相关性质研究[J].逻辑学研究,2010,(3):67-79.
[10]张晓君.广义量词的语义性质研究[D].北京:中国社会科学院,2011.
[11]张晓君.广义量词的各种单调性之间的关系[J].安徽大学学报(哲社版),2012,(5):47-52.
[12]PARSONS T.The Traditional Square of Opposition[EB/OL].[2012-06-18].http://plato.stanford.edu/archives/sum 2004/entries/square/,2004.
[13]QUINE W V.Selected Logic Papers[M].Harvard University Press,1995.
[14]WESTERSTåH1 D.The Traditional Square of Opposition and Generalized Quantifiers[J].逻辑学研究,2008,(3):1-18.
[15]张晓君,黄朝阳.广义量词的单调性与其三种否定量词的单调性之间的关系[J].安徽师范大学学报(人文社科版),2012,(6):673-678.
[16]张晓君,林胜强.如何利用广义量词的语义性质判断扩展三段论的有效性[J].逻辑学研究,2013,(2):42-56.
[责任编辑:张 卉]
B819
A
1000-5315(2015)01-0015-06
2014-08-12
国家社科基金重大项目“应用逻辑与逻辑应用研究”(14ZDB014)。
林胜强(1963—),男,四川隆昌人,四川师范大学政治教育学院副教授,主要从事语言逻辑和哲学逻辑的研究。
