基于多重参考模型的风电场风机尾流模拟

曾利华，张国

(河北省电力勘测设计研究院，石家庄市 050031)



基于多重参考模型的风电场风机尾流模拟

曾利华，张国

(河北省电力勘测设计研究院，石家庄市 050031)

为了研究三维旋转风轮的尾流流动情况，利用多重参考模型(moving reference frame，MRF)数值模拟给定风机的尾流情况，针对风机在不同的入口风速和桨距角的情况下，对其尾流流场的速度和压力分布进行了研究，发现风场的速度、压力分布及尾流、入口风速和桨距角变化对整个流场的影响与实际情况一致。该方法能预测风机运行性能和尾流湍流情况，并达到仿真风力发电机组气动流场的目的，用数值模拟的方法部分取代模型机的实验，既可缩短实验时间、节约实验成本、缩短研发周期，又能为机组运行提供可靠的建议。

风电场；风力发电机组；尾流；数值模拟；模型机

0 引 言

风电场三维流场的精确模拟相对比较复杂，主要包括风机叶片设计、风机建模、风电场建模及网格划分、风电场三维流场数值模拟的计算条件设定、风电场三维流场求解几个部分。Sung C H等[1]采用B-L零方程湍流模型计算了流场，并与试验数据进行了比较，得出此方法可以预测翼型前端的涡旋大小；Parneix S等[2]等通过v2f模型-修正标准的k-ε模型，并采用一定的假设而得，计算了翼型绕流的流场，并与Simpson等人的试验数据进行了比较，结果良好，特别是的翼型的边缘。Deng G等[3]采用新的Reynold应力模型Rij-ω模型也做了类似的工作。刘沛清[4]利用大涡模拟技术对不同来流攻角下的NACA0012翼型绕流进行了数值模拟，给出了翼型绕流分离流随攻角的变化特征和翼型在分离流中的气动参数；Gadel-Hak M等[5]对俯仰翼型进行了研究，发现当升力面在低速和高速流场内俯仰振动时，绕升力面的流场及气动力在其上仰和下俯相同迎角瞬间是不同的；褚洪杰[6]等选取4个线性湍流模式、4个非线性涡粘性湍流模式和1个显式代数应力模式对绕翼型的不可压缩分离流动进行了数值模拟；1993年，Menter F R等[7]提出了k-ωSST模型。该模型混合了k-ε和k-ω这2种模型，描述了剪切应力在具有逆压梯度的边界层的传输过程，该模型能适应压力梯度变化的各种物理现象；通过壁函数的应用，精确地模拟边界层的现象，无须使用较容易失真的粘性衰减函数。2000年，文献[8]提出了湍流模型分离涡模拟方法方法，综合了雷诺平均方程与大涡模拟的优点，使大雷诺数下大分离流动的数值模拟方法提高一大步。在近壁面雷诺平均方程的湍流模型特性，而在远壁面处表现为大涡模拟的亚格子模型的特点。但根据实际应用成果[9]情况来看，此种方法虽然能给出较详细的流场分布，但计算出的风机整体的气动性能并没有改观，且计算必须是非稳态的，需要耗费大量的计算机资源。曾利华等[10]只对尾流以及迭加模型进行了研究，尚未进行数值模拟。

实际情况下，在风的作用下，当升力大于阻力时，风机处于旋转状态。在旋转的作用下，旋转叶片的附面层内气流受离心力的作用而产生径向流，使得叶片翼型上的压力分布、速度分布远复杂于二维静止翼型的情况。在整个风电场中，若风机间的布置不合理，上游的风机尾流将可能影响到下游的风机的工作风速及稳定性。本文采用三维的数值计算方法研究风场的速度、压力分布及尾流，及入口风速和桨距角变化对整个流场的影响，使得数值模拟结果更加接近现实。

1 模型建立

1.1 风场模型的建立和网格划分

因风轮的转动对上游的影响较小，而对尾流的影响较大。计算区域选择上风向约为风轮直径5倍，下风向选择约风轮直径10倍，如图1所示。网格的划分采用非均匀的网格，因为在风轮附近区域空气的湍流度最大，变化最为复杂，因此需要对其进行局部加密处理，如图2所示。

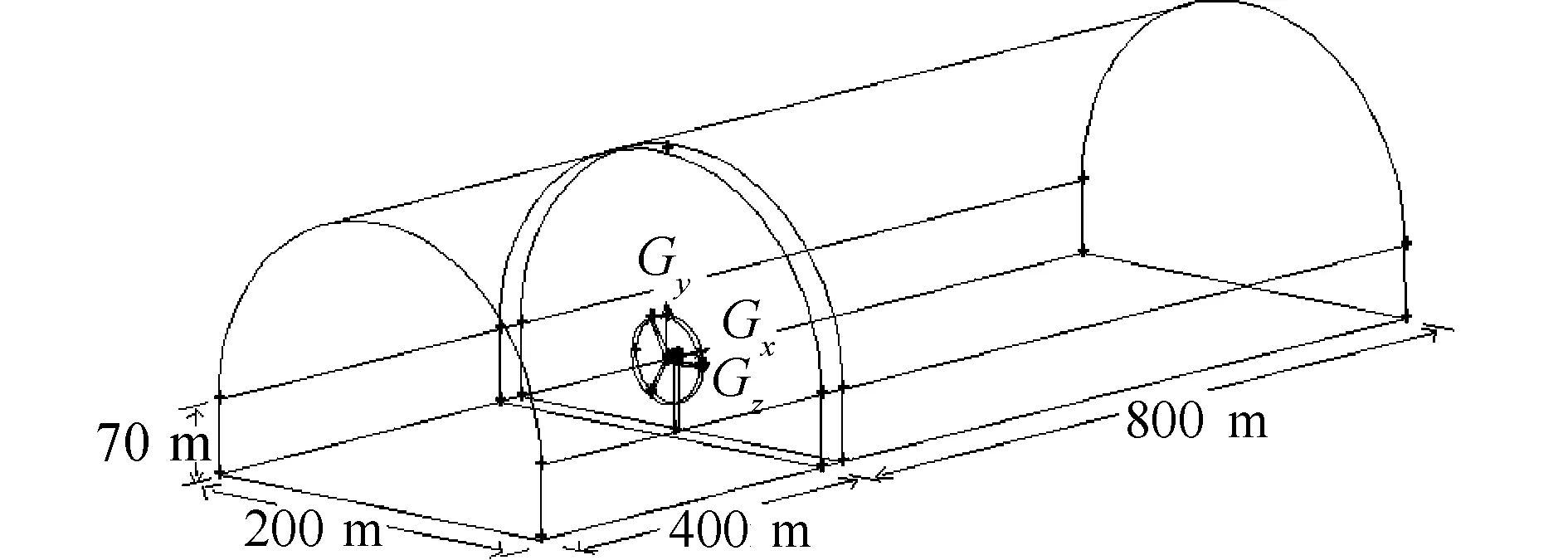
图1 风机及计算的区域

图2 计算区域的网格划分

1.2 风场数值求解

1.2.1 假定条件及求解方法

实际风机在正常的工作时，旋转叶片周围空气的具体流动状态及分布是未知，然而空气处于湍流状态是肯定的。在本文的研究过程中，将风轮放置在来流均匀不变的风洞中进行数值实验研究，也即

忽略了自然风均匀性、方向性和脉动性的影响。由于空气流经风轮过程中，温度变化不大，在极短的时间段内流场各物理量变化不大，马赫数也较低，故在计算过程中，假设研究湍流问题为稳态不可压缩空气流动问题，流动过程与外界无换热(即不考虑能量方程)。

本文采用三维稳态隐式解法，湍流模型采用较成熟的k-ε模型，对于近壁区域采用壁函数法，压力-速度耦合采用simple算法，离散格式采用二阶迎风格式。

1.2.2 边界条件

(1)由假设来流均匀可知，风洞入口可设定为速度入口条件。

(2)风洞出口为压力条件或自由出流。

(3)小控制体的加入是为了局部加密网格而引入的，小控制体的各面设定边界条件为interface(适用于网格不一致的情况)。

(4)风洞壁面选择边界条件为wall。对于粘性流动，物面速度采用无滑移条件。

1.2.3 转动条件

三维动态风场中，风机是不停转动的。实现流体的旋转，在Fluent中可以由MRF、Mixingplane、滑移网格和动网格技术来实现。由于研究问题中不存在静子和转子区域的区分，也无法界定混合面两面的进出条件，实现不了混合平面对的平均，因此Mixingplane技术无法实现；滑移网格一般用来解决非稳态问题，也强调交界面，这恰是研究问题所无法确切界定的问题，因此，该方法也不适合；动网格技术主要考虑到了边界发生形变的情况，而不是刚性边界，另外引入了自定义函数(user-definedfunction,UDF)等许多精确处理方法，对于本文的三维问题，采用动网格技术将非常复杂且必要性不是很大。故采用MRF来研究三维的旋转风场。

2 风场速度和压力分布

在数值计算中，风机叶片的转速假设不变，且额定转速为14.4r/min。以桨距角4.5°、入流速度13m/s的风场为例，采用MRF来研究三维的旋转风场，对其计算结果进行分析，如图3为其计算的各项参差的收敛过程。

2.1 叶片表面速度和压力分布

根据MRF的模拟结果，叶片表面迎风面与背风面的速度与压力分布图如图4、5所示。

如图4所示，风轮叶片的正、背面的风速分布是一致的，风轮半径越大，速度越大，满足速度与转速和

图3 各项参差的收敛过程

图4 风机叶片速度分布

半径的乘积关系。从图5可见，叶片的正面压力为正，且叶片正面翼型的前缘压力较大，而相对的后缘背面为负压，为空气从叶片绕流所致，正是叶片正反面的压力差促使风轮转动。

2.2 流场中各观测面速度分布

分别从x、y、z这3个方向观测到不同观察面的流速分布，如图6所示。

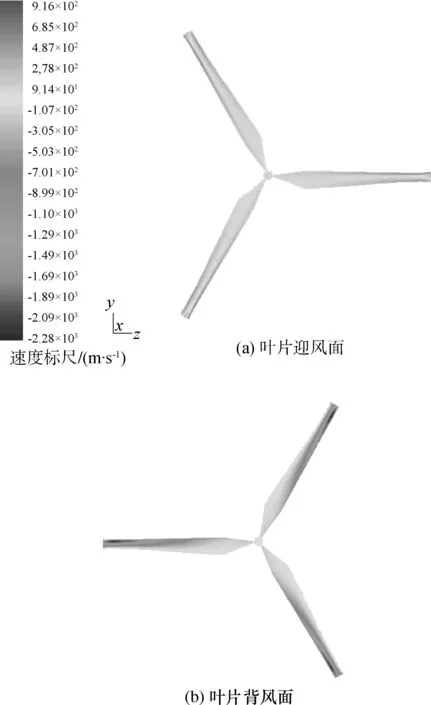
图5 风机叶片表面压力分布

由图6可知：

(1)旋转的风机存在复杂的尾流，而对其上游风场影响较小。图6(a) (b)给出的是z=0和y=0截面的速度图云(左)和等速线(右)分布，可以看出距风机越远，速度梯度的变化越小。这是由于旋转的风机吸收部分风能后，使得风速减小，这种风速减小的区域与下游对流，在尾流和自由气流之间风速梯度会引起附加的切变湍流，形成复杂的混合尾流，随着远离风机，这种尾流变得更宽更浅，直至这个气流在下游远处完全恢复(考虑到计算量太大，本文算例计算了风力机后的800 m的区域)。在风机和机架之后，风速较小，随着距离风机越远，风速越大，这是符合能量守恒方程。旋转的风机的阻挡作用，使得在风机前方附近区域风速有所降低，但影响范围很小。

(2) 由图6(a)与 (b)对比可见，图(b)中的等速线分布极为对称；由于地面和机架的影响，图(a)中的等速线呈不对称分布。地面对临近来流存在较大影响，降低了来流的风速；由z=0和x方向的各截面的速度分布分析，机架不仅降低其后风速，使尾流情况更加复杂，而且阻挡前方来流，降低了风速和改变了来流方向，从而影响风机的风能利用系数，这与实际情况较为吻合。因此，尽可能增加机架高度可降低地面对风机的影响，减小机架的迎风面积可减小对风场的影响范围。

图6 流场中各观测截面的速度云图和等速线分布

(3) 在风轮平面的等速度线如图6(c)所示，可见在叶轮周围等速线的密度较大，而在远离转轮周围区域，等速线较稀疏，主要是由于风力作用于叶轮，叶轮转动，引起速度与压力之间的转化梯度较大而引起的。

2.3 叶片周围速度和压力分布

根据MRF的模拟结果叶片表面迎风面与背风面的速度与压力分布图如图7～9所示。

图7 z=5 m截面处翼型周围压力和速度分布

图8 z=30 m截面处翼型周围压力和速度分布

从图7～9可知，靠近翼型前缘正面(下表面)压力较大，而在相对的背面(上表面)压力较小，甚至为负压；在速度分布图中，靠近翼型前缘背面速度较大，正面风速较小，与实际翼型特性也是吻合的。

3 桨距角变化对风场的影响

叶片桨距角是影响风机转矩和功率的重要参数，可以在叶根调节整个叶片的桨距角。本文计算出不同桨距角下的风机的转矩T，并由下式分别求出轴功率P和风能利用系数Cp:

图9 z=35 m截面处翼型周围压力和速度分布

P=Tω

(1)

(2)

式中：ω为叶片转速，rad/s；ρ为空气密度，kg/m3；υ为上游风速，m/s；S为风轮的扫风面积，m2。

风场入口风速(上有风速)保持设计风速13 m/s，风轮以额定转速14.4 r/min转动，桨距角的变化情况及其相应的计算结果如表1所示。

表1 不同桨距角下的扭矩、功率及风能利用效率的变化

Table 1 changes of torque, power and wind energy utilization efficiency under different pitch angle

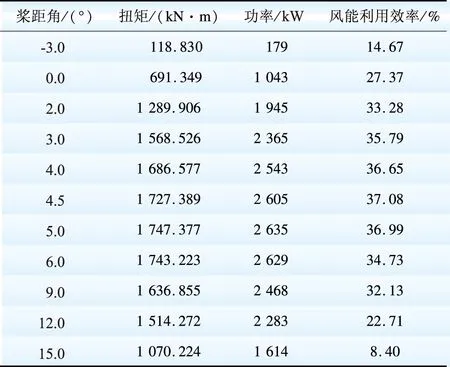
由表1分析可得，桨距角的微小变化对扭矩、功率及风能利用系数有显著的影响。随着桨距角的增加，三者先增大后减小，在桨距角为4.5°时，三者达到了最大。当风场入口风速为13 m/s，风轮以额定转速14.4 r/min转动，桨距角为4.5°时，设计的风机运行在最佳风能捕获状态。当进行正桨距角的调节时，将引起设计桨距角的增加，从而减少了攻角；相反，负桨距角的设置增加了攻角，而且可能导致失速的产生。

在设计风速和额定转速状态下，当桨距角大于最佳桨距角4.5°时，风场尾流的等速线分布较疏，这是因为此时攻角减小，来流沿叶片表面流过，对尾流影响变小；当桨距角小于最佳桨距角4.5°时，此时攻角增大，来流将脱离叶片表面，严重时将在叶片附近出现很明显的漩涡流动，引起失速，因此，风场尾流的等速线分布较密且变得更加复杂。

4 风速变化对风场的影响

风速因受各种因素影响不断变化，且风速变化将影响风力机功率和效率。为了研究风场中风速变化的影响，在桨距角分别为4.5°和9°时，对不同来流风速的风场进行了计算，如图10、11所示。

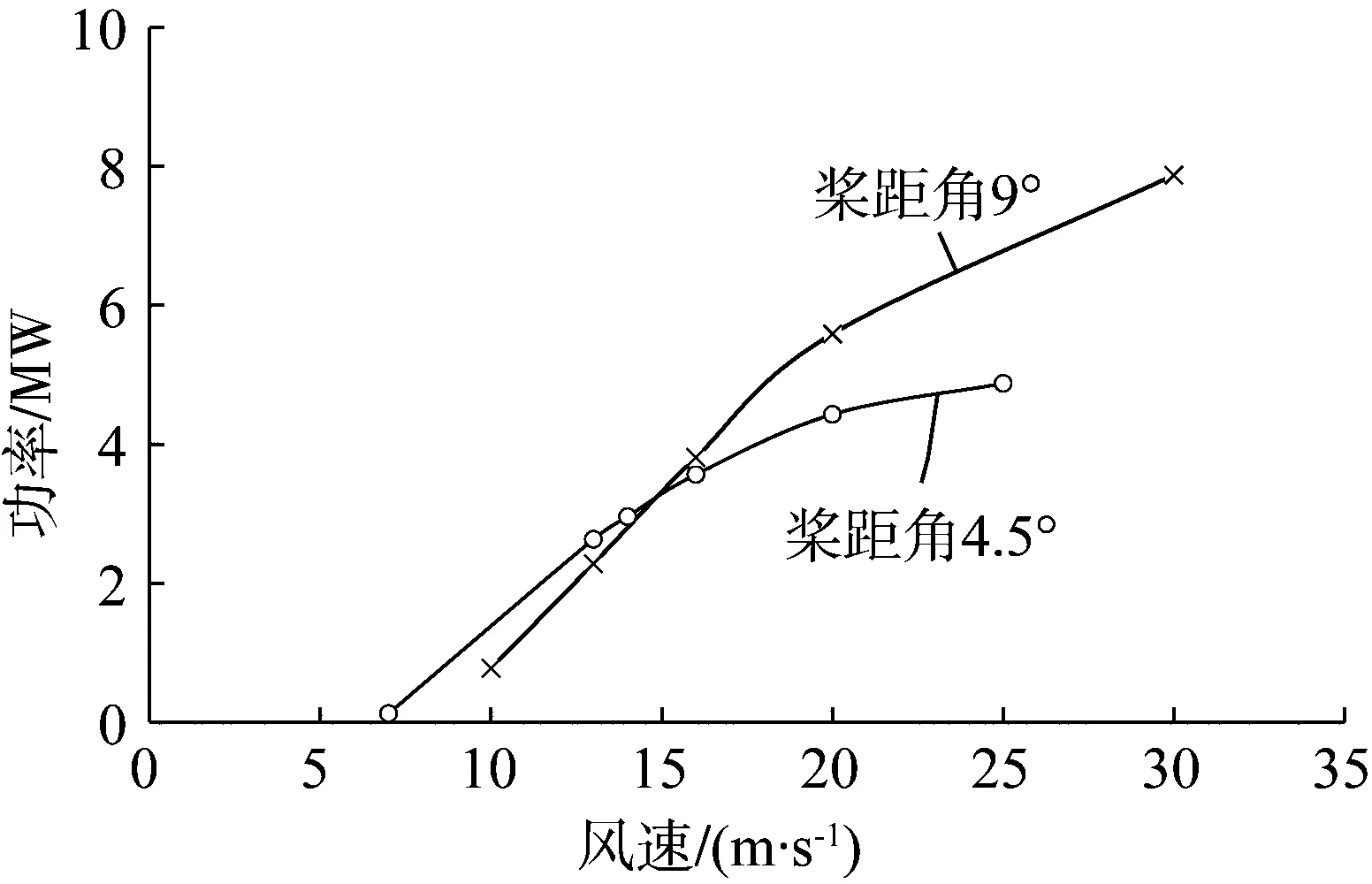
图10 风速变化对功率的影响

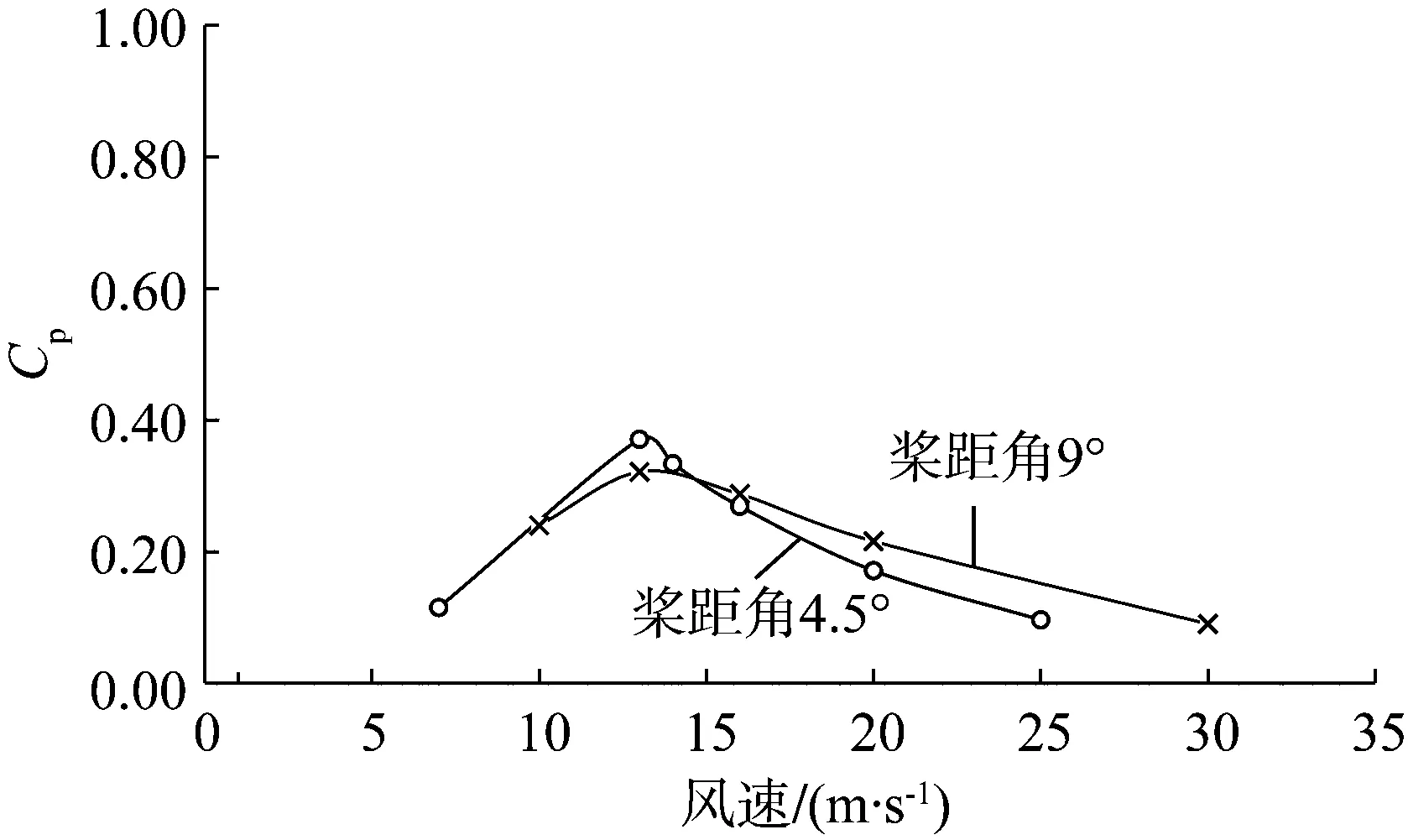
图11 风速变化对风能利用系数的影响

由图10可知：(1) 当风机在设计风速下以额定转速运行时，风轮将运行在最佳风能捕获状态。在桨距角一定时，入口风速减小时，来流攻角将减小，来流沿叶片表面流过，对尾流影响变小，所以尾流的等速线分布较疏，如图入口风速为7 m/s的尾流情况；相反，入口风速增大时，攻角将增大，来流将脱离叶片表面，严重时将在叶片附近出现很明显的漩涡流动，引起失速，因此，风场尾流的等速线分布较密且变得更加复杂，如图入口风速为16、25 m/s的尾流情况。(2) 在额定转速和桨距角一定时，随着风速增加，风机功率是一直增加的。这是因为风速增大，风机受力增加，从而使得扭矩和功率增大。

风能利用系数并非随风速增加而一直增大，而是先增大，当达到一定风速时，风能利用系数达到最高，随后逐渐减小。由图11可知，在设计风速13 m/s时，风能利用系数达到了最大，这说明设计和数值计算的结果是吻合的，与实际风场情况是相符的，因此，设计和数值计算结果均是可信的

5 结 论

(1)三维动态数值模拟计算能有效地反映风场的压力和风速分布，能较好显示出风机叶片附近的流场分布及尾流情况；桨距角和入流风速变化对尾流有很大影响。与处于设计风速、额定转速状态和最佳桨距角的状态相比，当桨距角增大和风速减小时，来流攻角减小，来流沿叶片表面流过，对尾流影响变小；当桨距角减小和风速增大时，来流攻角增大，来流将脱离叶片表面，严重时将在叶片附近出现很明显的漩涡流动，引起失速，因此，风场尾流的等速线分布较密且变得更加复杂。

(2)计算结果表明，桨距角的微小变化对扭矩、功率及风能利用系数有显著的影响。随着桨距角的增加，三者先增大后减小，在桨距角为4.5°时，三者达到了最大；入口风速增大时，风机功率一直增大，而风能利用系数先增大，在风速为13 m/s时达到最大，随后减小。

(3)当风场入口风速为13 m/s，风轮以额定转速14.4 r/min转动，桨距角为4.5°时，设计的风机运行在最佳风能捕获状态，这说明设计和数值计算的结果是吻合的，与实际风场情况是相符的，因此，设计和数值计算结果均是可信的。

[1]Sung C H, Yang C.Validation of turbulent horseshoe vortex flows[C]//17th Symposium on Naval Hydrodynamics.Hague: Maritime Technical Information Facility, 1988: 103-118.

[2]Parneix S, Durbin P A, Behnia M.Computation of 3d turbulent boundary layers using the v2-f model[J].Flow Turbul Combust，1998, 60(1)：19-46.

[3]Deng G, Visonneau M.Computation of a wing-body junction flow with a new Reynolds-stress transport model[M].Washington DC: National Academies Press, 1999: 691-707.

[4]刘沛清,邓学蓥.绕翼型分离流结构的数值研究[J].航空学报, 1997, 18(4): 385-389.Liu Peiqing, Deng Xueying.Numerical study of separated flows over an isolated airfoil[J].Acta Aeronautica Et Astronautica Sinica, 1997, 18(4): 385-389.

[5]Gadelhak M.The Pitch Delta Wing[J].AIAA Journal, 1985, 23(11): 1160-1165.

[6]褚洪杰, 马晖扬.应用于翼型绕流的线性/非线性湍流模式的研究[J].空气动力学学报, 2005, 23(2):237-242.Chu Hongjie，Ma Huiyang.Linear and nonlinear turbulence models for simulation of the flows around airfoil[J].Acta Aerodynamica Sinica，2005, 23(2):237-242.

[7]Menter F R.Multiscale model for turbulent flows[C] //24th Fluid Dynamics Conference.Orlando: American Institute of Aeronautics and Astronautics, 1993: 1311-1320.

[8]AIAA 2000-2306.Trends in turbulence treatments[S].Denver: American Institute of Aeronautics and Astronautics, 2000.

[9]Johansen J, Sorensen N N, Michelsen J A, et al.Detached-eddy simulation of flow around the NREL phase VI blade[J].Wind Energy, 2002, 5(2-3):185-197.

[10]曾利华,王丰,刘德有.风电场风机尾流及其迭加模型的研究[J].中国电机工程学报,2011, 31(19):37-42.Zeng Lihua ,Wang Feng ,Liu Deyou .Study WTG wake model and WTG overlay model in wind farm[J].Proceedings of the CSEE, 2011,31(19):37-42.

(编辑：蒋毅恒)

Wake Numerical Simulation of Wind Farm Based on MRF

ZENG Lihua，ZHANG Guo

(Hebei Electric Power Design & Research Institute, Shijiazhuang 050031, China)

In order to study the wake flow of 3D rotating rotor, this paper numerically simulated the wake of a given fan by using moving reference frame (MRF).The velocity and pressure distribution of wake flow field under different inlet wind velocity and pitch angles were studied for wind turbine generator.It is found that the influences of wind field velocity, pressure distribution, wake, inlet wind velocity and pitch angles changes on the whole flow field are consistent with the actual situation.This method can forecast the running performance and wake turbulence of wind turbine, and achieve the simulation of the aerodynamic flow field of wind turbine.Using numerical simulation method to replace part of model machine experiments can shorten the experiment time, save the experiment cost, shorten the development cycle, and can provide reliable suggestions for the operation of units.

wind farm; wind turbine generator; wake; numerical simulation; model machine

TM 315

A

1000-7229(2015)08-0135-06

10.3969/j.issn.1000-7229.2015.08.022

2015-04-20

2015-05-27

曾利华(1984)，女，硕士，中级工程师，主要从事风电场设计工作；

张国(1981)，男，硕士，中级工程师，主要从事机械设计工作。