揭秘球在点光源下的投影

王常庆

(新疆阿勒泰地区第一高级中学，836500)

在高中阶段我们学习圆锥曲线时，对“圆锥被不同的平面切割而获得不同的圆锥曲线”的理解往往比较抽象,教材又没有给出系统的证明,对学生的学习有一定的困扰.课堂教学中是否有更直观、更容易操作的模型来刻画圆锥曲线的来源及其不同形式呢?

在实践中我们发现,放置于桌面上的球,在手电筒的照射下,其投影会随手电筒的位置变换呈现不同的形状,有圆形,有椭圆形,也有非封闭曲线.这些投影会是真正的圆锥曲线吗,如何证明?对光源的位置有何要求?下面我们就来揭开它神秘的面纱.

如图1,设S为点光源,在S的照射下,球O在平面α上的投影的轮廓线为曲线L.从S发出的所有与球O相切的光线恰好形成一圆锥的侧面,球O刚好内切于该圆锥.球O与光线的所有切点刚好形成一个封闭的圆,记作⊙O1[1].

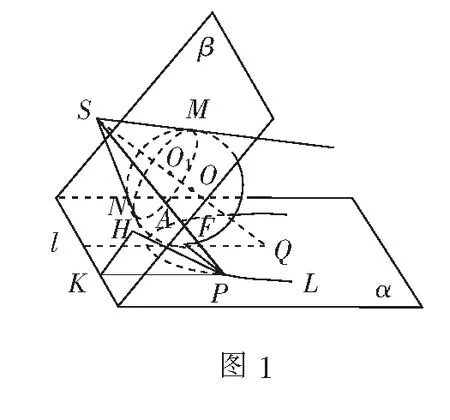
易知,当S在球O的正上方时,曲线L是一个圆.下面重点探究S不在球O的正上方时的情形.

当点光源S不在球O的正上方时,⊙O1所在平面β必与平面α相交,设α∩β=l,球O与平面α相切于点F,当球O大小及点S位置固定时,l为定直线,F为定点.SO1⊥β,OF⊥α.又设SO交α于点Q,则l⊥面O1QF(S，O1，O，Q，F共面).在投影轮廓线L上任取一点P,过点定P作PH⊥β于点H,此时PH∥SO;又作PK⊥l于点K,连结PS交⊙O1于点A.连结HK，HA,则∆PHK，∆PHA均为直角三角形，且∠KPH=∠SQF，∠SPH=∠PSQ,其中∠SQF，∠PSQ分别表示平面α与圆锥轴线所成的角和圆锥的半顶角,分别记作θ1和θ2(均为锐角)即∠KPH=∠SQF=θ1,∠SPH=∠PSQ=θ2.

因为PF，PA均为球O的切线,所以

|PF|=|PA|.

①

又在Rt∆PHK中，有|PH|=|PK|·cos∠KPH；在Rt∆PHA中,|PH|=|PA|·cos∠APH.故

②

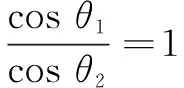
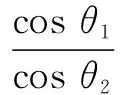
另设⊙O1上距平面α最远点为M,最近点为N(图1),则MN⊂面OQF,且∠MSO=θ2,∠SQF=θ1.所以,当θ1=θ2时,曲线L表示抛物线,SM∥QF,此时,点光源S距平面α高度恰等于球O直径;同理,当θ1>θ2,曲线L表示椭圆,点光源S距平面α高度大于球O直径;当θ1<θ2,曲线L表示双曲线(一支),点光源S距平面α高度小于球O直径.