基于散射特性的混装箔条云RCS计算与仿真*

李亚飞 潘莉莉

(1.海军航空工程学院研究生管理大队 烟台 264001)(2.海军航空工程学院科研部 烟台 264001)



基于散射特性的混装箔条云RCS计算与仿真*

李亚飞1潘莉莉2

(1.海军航空工程学院研究生管理大队 烟台 264001)(2.海军航空工程学院科研部 烟台 264001)

目前对箔条云雷达散射截面(RCS)计算多采用经验公式,难以满足混装箔条弹RCS的精确计算需求,针对这一问题提出了基于散射特性的混装箔条云RCS精确计算方法。结合单根箔条的散射特性和姿态特性,对不同极化条件下单根箔条和箔条云的RCS进行精细化求解,为箔条弹的配比和RCS计算提供了模型基础。MATLAB仿真结果表明,模型能够满足混装箔条云RCS的精确计算,为精确研究箔条干扰提供了数据支持。

散射特性; 混装箔条云; 箔条云雷达散射截面

Class Number TN974

1 引言

箔条干扰是无源干扰中一种有效的干扰手段。为得到有效的箔条干扰,就要保证箔条云由足够的RCS诱使雷达偏离目标。目前对箔条云RCS的计算多是对半波长箔条云根据经验公式求解[1～4]

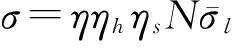
半波长箔条的谐振峰都很尖锐,适用的频带很窄,其带宽一般只有中心频率的15%～20%。在战场环境中,难以预测敌方雷达的准确频率,因此为做到干扰频率的连续覆盖,一般采用混装箔条弹进行无源对抗。经验公式只能计算单波段半波长箔条形成箔条云的RCS,却无法计算混装箔条云的RCS。因此研究不同长度箔条对单频入射波的散射截面积就至关重要。本文提出了基于散射特性的混装箔条云RCS计算方法,结合单根箔条的极化散射特性,求得单根箔条在不同姿态、不同极化条件下的RCS,根据箔条的空间分布统计特性和姿态统计特性,可以精确计算混装箔条云在不同极化条件下的RCS。

2 箔条的散射特性[5～6]

图1 极化坐标系下偶极子散射示意图

箔条云可以看成由大量偶极子散射体组成的云团,因此,对其散射特性的研究需要从单根箔条偶极子出发。以单根偶极子的中心为原点,以入射电场方向为nT轴,以水平极化方向为eH轴,以垂直极化方向为eV轴,建立极化坐标系[7]如图1所示。极化坐标系中,箔条偶极子散射电场为Esc,散射电场曲面是关于箔条轴对称的,取其极化方向为偶极子的空间取向矢量d在极化坐标系平面内投影方向的反向,d在极化坐标系下的方位角为α。

箔条散射电场Esc的极化方向eΘ在极化坐标系中表示为

在极化坐标系中,任意极化入射电场Ein可以表示为:Ein=Eh1·eh+Ev1·ev,假设入射电场在散射平面内的电场分量为E0,则E0可表示为

根据电磁散射理论,偶极子的散射电场Esc为

其中,Θ为入射电场方向nT与偶极子取向d的夹角,k=2π/λ,λ为入射波波长,r为偶极子与雷达的距离,f(Θ)为偶极子散射电场的方向性函数,其表达式见文献[8]。

由于

3 单根箔条的RCS值求解

根据雷达极化理论[9],可得

式中:sHH表示水平极化入射场产生水平极化散射场的散射系数；sHV表示水平极化入射场产生垂直极化散射场的散射系数。sVH表示垂直极化入射场产生水平极化散射场的散射系数；sVV表示垂直极化入射场产生垂直极化散射场的散射系数。

不同极化条件下单根箔条的RCS值如下

(1)

式中:σHH为水平极化照射同极化接收的RCS,σHV为垂直极化照射水平极化接收的RCS,σVH为水平极化照射垂直极化接收的RCS,σVV为垂直平极化照射同极化接收的RCS。为求不同极化条件下单根箔条的RCS,需要求得各散射矩阵的值。

图2 全局坐标系下偶极子散射示意图

在单根箔条RCS求解中建立全局坐标系如图所示,以箔条中心为坐标原点,xoy平面为水平面,y轴可选为正北方向,z轴方向垂直向上。假定箔条的取向矢量为d,其方位角为φd,d与z轴正向的夹角为θd。散射电场的方向为nR,其方位角为φs,nR与z轴正向夹角为θs。对于单站箔条后向散射的情况,入射电场传播方向与散射电场相反,即nR=-nT。

箔条的取向矢量d在空间坐标系下的坐标为

d=[cosφdsinθdsinφdsinθdcosθd]

散射电场的传播方向为

nR=[cosφssinθssinφssinθscosθs]

根据方向余弦定理,可得d与nR的夹角Θ满足:

cosΘ=sinθdsinθscos(φd-φs)+cosθdcosθs

由空间几何关系,经推导可得

d·eH=sinθdsin(φd-φs)

d·ev=cosθssinθdcos(φd-φs)-sinθscosθd

代入式子可得

(2)

其中

a11=sin2θdsin2(φd-φs)

a12=a21= sinθdsin(φd-φs)[cosθssinθdcos(φd-φs)

-sinθscosθd]

a22=[cosθssinθdcos(φd-φs)-sinθscosθd]2

将式(2)代入式(1)即可求得单根箔条在任意极化条件下的RCS。

4 箔条云RCS求解

箔条云RCS由单根箔条RCS求和而成。在箔条云形成初期,由于箔条距离过小,它们会相互作用,即产生互耦,使散射波减小,这就是互耦效应(遮挡效应)。经过一定时间之后,当箔条间隔平均大于2λ时,可以忽略互耦效应。为方便计算,假设箔条云已经充分散开,互耦效应可以忽略,而且都位于雷达波束范围内,箔条云团处于稳定状态,近似认为在纵向、横向、高度上均服从正态分布。

式中:x0,y0,z0为箔条云团中心点坐标,σx,σy,σz为箔条在三维方向的方差。

由单根箔条RCS分析可知单根箔条的散射特性与箔条的空间位置、姿态有关。箔条云方位角在0～2π范围内服从均匀分布,而箔条俯仰角则相对集中于某一倾角,具有一定的分散程度[10]。根据以上的位置关系,可以求得在雷达波束内每根箔条的回波RCS。

设N为箔条云团中总的箔条数目,则箔条云的总的RCS可表示为

(3)

因此,该方法可以求得不同长度、不同极化方式、不同配比箔条云的RCS。

5 仿真分析

为验证计算模型的效果,分别对单种箔条弹在不同极化特性下RCS和混装箔条弹在特定极化条件下的RCS进行仿真。

1) 单种箔条弹在不同极化特性下散射截面

假定箔条水平取向φd在(0,2π)服从均匀分布,俯仰角θd服从水平正态分布(均值为0,方差为10°),箔条数目为10000。箔条中心位置为(6000m,6000m,300m),空间散布服从正态分布,方差为60m。雷达位于原点位置,天线对准箔条云中心,不同收发极化方式对应的箔条总的RCS如图3所示。取入射波长λ=3.5cm,而箔条长度l为变量,横坐标是箔条长度与波长的比值,纵坐标为取对数后箔条云RCS与λ2的比值。

图3 单种箔条弹在不同极化特性下的RCS

仿真结果显示,箔条云总的RCS在l/λ接近0.5和1时有较大的RCS值,该结果与文献[6]中仿真结果一致,由于箔条缩短效应,箔条在接近半波长的整数倍附近谐振,有较大的RCS。不同极化条件下箔条云的RCS不同,σHH>σHV>σVV,由于箔条云姿态服从水平正态分布,对水平极化照射同极化接收的雷达干扰效果较好,对垂直极化照射并且垂直极化接收的雷达干扰效果较差。

2) 混装箔条弹的散射截面

为覆盖较宽的干扰频带,箔条弹一般会混装多种长度的箔条,为了便于生产,箔条弹中箔条长度种类不宜太多,一般为5～8种[9]。表1为假定的箔条弹混装信息。

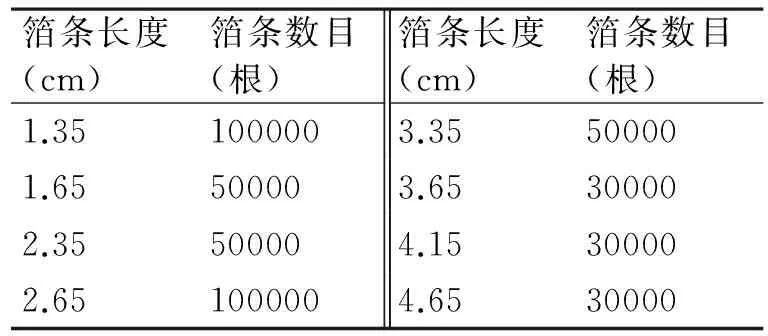
表1 箔条弹混装信息

图4 混装箔条弹散射截面的频率响应

箔条中心位置为(6000m,6000m,300m),每种长度的箔条在空间内散布均服从正态分布,方差为60m。箔条取向角φd在(0,2π)服从均匀分布,θd服从水平正态分布(均值θc=0°,方差为10°),雷达频率为变量,由以上的仿真模型可得混装箔条云在HH极化条件下总的RCS对频率的响应曲线如图4所示。仿真结果表明,混装箔条弹的覆盖频带范围为3GHz～14GHz,其RCS起伏不超过20%,对于多种频率的雷达具有较好的干扰效果。

6 结语

本文从单根箔条的散射特性出发,结合箔条的姿态特性,得到单根箔条在不同极化特性下的RCS精确计算模型。根据箔条云与雷达的位置信息可以得到混装箔条云的RCS。仿真结果表明,该模型能计算不同极化,不同混装条件箔条云的RCS,为箔条弹的配比和RCS计算提供参考。为贴近实际,模型条件设定可以更加复杂,通过设定箔条云的运动特性以及切割效应可以精细化地模拟箔条云RCS的动态变化特性,还可以根据箔条RCS与回波幅度的关系进一步对箔条云的回波进行精细化仿真。

[1] 陈静.雷达无源干扰原理[M].北京:国防工业出版社,2009:96-97.

[2] 李星,赵宏钟.箔条云团扩散过程的建模仿真[J].现代电子技术,2011:16-18.

[3] 骆永军,赵岩泉,王基组.基于粒子系统的雷达箔条干扰仿真[J].火力指挥与控制,2004,29:75-77.

[4] 吕萌萌.箔条云电磁特性研究及仿真软件设计[D].西安:西安电子科技大学,2012:19-20.

[5] 李金梁,王雪松,李永祯.箔条云散射的极化统计特性[J].电子学报,2010,38(3):714-719.

[6] 瓦金CA,舒斯托夫.无线电干扰和无线电技术侦察基础[M].《无线电干扰和无线电技术侦察基础》翻译组译.北京:科学出版社,1977:257-258.

[7] 李金梁.箔条干扰的特性与雷达抗箔条技术研究[D].长沙:国防科学技术大学,2010:54-55.

[8] Anton Nagl. Radar cross section of thin wires[J]. IEEE Transaction on Antennas and progat.,1991,39(1):105-108.

[9] 陈静.雷达箔条干扰原理[M].北京:国防工业出版社,2007:181-183.

[10] Marcus Sherman W. Dynamics and radar cross section density of chaff clouds[J]. Aerospace and Electronic Systems, IEEE Transactions on,2004,40(1):93-102.

Computation and Simulation of Mixed Chaff Cloud RCS Based on the Scattering Characteristics

LI Yafei1PAN Lili2

(1. Brigade of Postgraduate, Naval Aeronautical Engineering Academy, Yantai 264001) (2. Department of Scientific Research, Naval Aeronautical Engineering Academy, Yantai 264001)

According to the situation that many current computation of Chaff cloud’s RCS use empirical formula and can hardly meet the computing need of mixed chaff RCS, a precise computation method is proposed. The scattering and posture characteristics of a single chaff is studied, to get a fine solving of single chaff and chaff cloud’s RCS under different polarization, which provides a computing model for chaff ratio and RVS computation. The simulation in Matlab shows that this model can afford accurate calculation of mixed chaff, and can provide data support for future precise research of chaff jaming.

scattering characteristics, mixed chaff cloud, RCS

2014年7月13日,

2014年8月25日

李亚飞,男,硕士研究生,研究方向:武器系统与运用,箔条仿真。潘莉莉,女,助理研究员,研究方向:武器装备仿真。

TN974

10.3969/j.issn1672-9730.2015.01.022