空运装载问题求解方法研究*

赵鸿飞 齐玉东 司维超

(1.91395部队装备处 北京 102443)(2.海军航空工程学院兵器科学与技术系 烟台 264001)



空运装载问题求解方法研究*

赵鸿飞1齐玉东2司维超2

(1.91395部队装备处 北京 102443)(2.海军航空工程学院兵器科学与技术系 烟台 264001)

针对空运装载问题,重点研究多目标多载具装载问题的数学模型,并提出基于重量差优先的禁忌邻域搜索优化算法来求解模型。实验结果表明该算法不仅保证目标函数值不恶化,还使得解空间搜索时间大大减少,极大地提高了模型求解速度。

空运装载; 多目标; 重量差优先; 禁忌邻域搜索; 优化

Class Number TP202

1 引言

物资空运装载问题可以描述为：给定一组需要运输的货物以及一组可实施运输的飞机,通过合理安排货物在各个飞机上的位置,在满足空间条件、重量条件和飞行平衡限制条件等基础上,以最小代价(常具体化为最少飞机数目)实现物资的全部运输。

国内对物资装载问题的研究多集中在单个载具的货物装载方面,对多飞机多约束条件下的货物装载方案的研究还不是很成熟。文献[1]通过构建空间布局转化模式,将空间布局约束转换成0-1整数线性约束,实现了对0-1数线性空运装载问题的求解,但如果问题规模较大,受限于整数规划算法,容易出现解空间巨大,不容易找到最优解。在军事装载问题研究方面,文献[2]在分析航空兵空运转场和转场物资特点的基础上确定了转场物资集约化装载方案制定方法提出集约化装载方案制定流程。文献[3]运用遗传算法,采用降维、物资集约等策略,研究了军事空运二维装载问题。文献[4]考虑了飞机重心、装货顺序和物资承压等约束条件,使用禁忌搜索算法对空运装载问题进行了求解,但仍有其它一些约束如飞机费用、货盘位置和飞机加油后对重心的影响等没有加以考虑。文献[5]针对陆路和水路形式的集装箱装载问题,分别建立了装载模型并给出了求解算法。文献[6]研究了民航货运装载问题,在维度方面采用了二维装载方案,但没有考虑装载物资对货机重心的影响。文献[7]针对当前军事物资装载与运输问题,映射建立数学模型,运用两次禁忌搜索算法自动输出较优的可行运输方案。第一次禁忌搜索用于确定较优的初始解,然后针对初始解,运用第二次禁忌搜索,保证在一定时间限制条件下,对运输问题进行优化求解。在军事装载问题研究方面,文献[8]以军用物资飞机装载为研究对象,构造军用物资的装载优化模型,并考虑装载容积、装载质量及装载密度等约束条件,提出了一种基于启发策略的遗传算法。

上述研究表明载具装载物资需满足一定的限制条件,如何综合考虑载具数量、载具平衡条件和运输成本,以形成物资装运方案是一个有着重要应用意义的研究方向。

本文重点研究在货物已经被打包,并可以合适的放置在飞机货盘上的前提下的空运装载优化问题,包括：

1) 如何将货物分组；

2) 如何选取合适的一组飞机,包括飞机类型以及飞机数量；

3) 如何将货物放置在合理的位置上,并满足飞机的配重要求。

2 Roesener数学模型

Roesener等[9～10]对空运装载问题进行了深入的研究,给出了数学模型和求解算法,不妨将该数学模型称为Roesener模型。Roesener模型主要包含目标函数、约束条件以及一些相关子过程的计算方法,其中,目标函数综合考虑了飞机数量、飞机重量、空间以及平衡性的限制等条件下的物资装运代价。

2.1 变量定义

表1 物资装载模型中的变量说明

在给出模型之前,首先给出模型中用到的变量及其说明,如表1所示。

2.2 目标函数

(1)

2.3 约束条件

除了以上目标函数最小化带来的动态限制,在算法求解中,还需要下面的运算基本约束。

1) 重量约束

对于每一架飞机,所载货物的总重均不能超过飞机的载重量。可以表示为

(2)

其中Wj表示第j架飞机的载重量上限。

2) 货位数量约束

对于每一架飞机,所载货物打包数量不能超过每一架飞机上的货位数目。

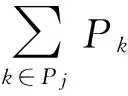
(3)

其中Pj表示第j架飞机的货位数目。Pk∈[0,1],0表示当前货位没有货物,1表示有货物。

3) 横向重心偏移约束

横向重心偏移尽管在一定范围上是允许的,但在算法运算中,为了增加运算速度,仍需要进一步限制这一偏移的大小。有以下约束：

W_CBj,min≤W_CBj≤W_CBj,max

(4)

其中W_CBj,min和W_CBj,max分别为飞机j的横向重心边界值。

4) 纵向重心偏移约束

与横向重心偏移约束类似：

H_CBj,min≤H_CBj≤H_CBj,max

(5)

其中H_CBj,min和H_CBj,max分别为飞机j的纵向重心边界值。

3 Roesener算法分析

为了求解多目标下多载具物资装载问题,Roesener等运用两次禁忌搜索算法得到可行运输方案,不妨将此算法称为Roesener算法。访算法将第一次禁忌搜索用于确定较优的初始解,然后针对初始解,运用第二次禁忌搜索,保证在一定时间限制条件下,对运输问题进行优化求解。

3.1 初始解产生方法

较优的初始解方案意味着,对于每架飞机,要保证其空间利用和负荷载重货物同时达到最大化。基于上述考虑,在第一次禁忌搜索中,Roesener算法试图通过让每一个飞机同时获得最大载重量和最大体积,以较低的计算代价来产生一个高质量的初始解。其评定标准为：当添加任意一个货物,飞机就会超重则认为是飞机获得了最大载重量；当所有货位被占用就认为是获得了最大体积。

3.2 第二次搜索

第二次禁忌搜索是在第一次搜索得到的初始解的基础上,考虑重心越界问题,其目标是,在满足各种限制的前提下,选择目标函数最小的最优方案。Roesener算法使用了一种动态邻域选择机制,在不同的运行上下文中根据飞机装载货物情况来选择合适的邻域操作。

经过第二次禁忌搜索的邻域移动,根据飞机的重心调整了飞机货物载量,并以最小化目标函数为指标,得到最终的装运方案。

4 两次禁忌搜索算法的改进

Roesener算法虽然求解了多目标下多载具物资装载问题。但当存在大量物资需要装载于多架飞机时,算法的执行效率随着问题规模变大而出现明显下降。通过追踪算法的执行过程,发现其90%以上的时间都花费在邻域搜索上面,这是因为邻域搜索时间与物资数量、飞机数量和货盘数量均成正比关系。因此,为了提高Roesener算法的效率,邻域搜索算法还需进行优化,优化的方向就是在目标函数值不出现恶化的前提下,尽量减少搜索时间。

4.1 算法改进的依据

待装载物资首先要进行规格化为包装体(pallet),然后将其固定到飞机货位上。一般的,同种型号的飞机,其货位数是固定的。在二次禁忌搜索优化的过程中,当前装载方案的邻域可以定义为：如果两个货位(并不局限于同机)不同时为空,那么交换这两个货位后的新装载方案,即为当前装载方案的一个邻域。

定义一个二元组pallet(aircraft_id,position),其中元组中的第一个元素为飞机编号,第二个元素为货位放置的pallet编号。那么货物可以用一个二元组pallet(aircraft_id,position)来表示,如第3架飞机的第5个货位,可以标示为pallet(3,5)。任意交换两个货位上的货物后的方案,即为当前方案的一个邻域。

为了提高禁忌算法的搜索速度,必须降低运算的集群规模,具体来说就是减少需要计算花费的邻域个数。单步跟踪Roesener算法的搜索结果,发现每次邻域搜索得到的具有最低花费的最优邻域,其所属的交换位置的pallet都具有较大的重量差,而且绝大部分是当前所有邻域中重量差最大的。

根据这一线索,仔细分析目标函数,可以发现pallets的重量影响五个费用因素中的三个,也就意味着重量是目标函数中的关键敏感性因素,较大的重量差将显著影响目标函数的取值。因此,重量因子相对于目标函数的其他变量因子,具有较大的影响力,也即,目标函数对重量相对更加敏感。显然,在邻域禁忌搜索中,具有较高敏感性的重量差越大的两个pallets交换,将优先成为当前邻域的最优计算方案。

4.2 改进方法

基于上述思想,本文提出基于重量差优先的禁忌邻域搜索算法,即在邻域搜索过程中,通过排除重量差较小的pallets位置交换,减少邻域计算搜索的次数,从而加快禁忌搜索的时间,具体方法如下所述。

1) 保证交换的货位不全为空

实际邻域搜索过程,两个空位置的交换是没有意义的。为了保证要交换的货位不同时为空,定义这样一个二元组：(pallet_num,position)。其中pallet_num代表pallet编号,position代表货位编号(相对于全部飞机而言)。

对于(pallet_num,position)二元组,其对应的邻域为：编号为pallet_num的pallet所在的货位编号position和其它position交换后的方案。这样就可以保证要交换的两个位置不同时为空。

2) 计算当前方案邻域的重量差值表

遍历所有邻域,并根据各个邻域的交换属性,计算其重量差,最终形成重量差值表。实际搜索过程中,相对于计算对应的邻域方案花费的计算量,关于pallet重量差的计算量,可以忽略不计,因此该方法是可行的。

3) 提取重量差较大的邻域,并计算其代价

由于重量并不是目标函数的唯一敏感变量,而只是其中较为敏感的一个,为了平衡其他敏感变量的影响,需要提取多个而不是唯一的一个邻域。根据设定的提取比例,提取重量差最大的邻域方案,并计算提取的邻域花费。

4) 根据当前的邻域花费代价,进行邻域禁忌搜索计算。

5 实验验证

为了比较基于重量差优先的邻域搜索算法和Roesener算法,本节应用文献[10]中使用的部分原始实验数据,分别应用两种搜索算法,以验证前者的优越性。

根据上述邻域优化方法,设定不同的邻域计算百分比p,进行二次禁忌搜索,并根据结果方案,计算其相关评估参数如表2所示。

表2 不同参数的搜索方案评估

由表2可知,第一次禁忌搜索得到的方案,最大利用了飞机的货舱空间和负荷载重货物,但由于没有考虑飞机的重心偏移问题,方案并不一定是可行解,经过第二次禁忌搜索的邻域移动,根据飞机的重心调整了飞机货物载量,并以最小化目标函数为指标,得到表2所示的二次较优的可行装运方案。

可见,通过设置适当的提取比例,将会极大地减少计算量,同时又不影响最终的计算结果。另外二次搜索可以显著的降低初始方案的目标函数值(20.3%),减少运输成本。

6 结语

为了高效求解物资空运装载问题,本文针对所建立的数学模型,提出了基于重量差优先的禁忌邻域搜索优化算法,实验结果表明在二次搜索过程中,采用邻域优化算法处理的搜索方案,可以使得搜索时间大大减少,实验结果验证了该算法的可行性和优越性。

[1] 孟冲,宋华文,陈柏松.规划的军事空运装载优化算法[J].西南交通大学学报,2011(3):500-505.

[2] 张克举,孙波,刘天宝.航空兵成建制空运转场集约化装载方案研究[J].科技信息,2012,33:636-637.

[3] 孟冲.航空兵应急转场空运装载方案优化研究[D].西安:空军工程大学,2009.

[4] 张军.军事空运装载问题的禁忌搜索算法实现[J].国防交通工程与技术,2010,8(6):32-35.

[5] 张劫.航空货运装载问题算法设计与研究[J].计算机工程,2007,39(5):28-30.

[6] Mongeau Marcel, Bes Christian. Optimization of aircraft container loading[J]. IEEE Tractions on Aerospace and Electronic Systems,2003,39(1):140-150.

[7] 齐玉东,谢晓方.基于两次禁忌搜索的军事物资装运方案研究[J].计算机工程与设计,2012,33(7):2766-2770.

[8] 周柯雯,姚爱祥基.基于遗传算法和启发策略的军用物资飞机装载优化[J].物流科技,2010(9):122-124.

[9] Nance R. L., Roesener A. G., Moore J T. An Advanced Tabu Search Approach to the mixed payload Airlift Loading Problem[J]. Journal of the Operational Research Society,2011,62(2):337-347.

[10] Roesener A. G., Hall S N. A Nonlinear Integer Programming Formulation for the Airlift Loading Problem with Insufficient Aircraft[J]. Journal of Nonlinear Analysis and Optimization: Theory & Application,2014:87-92.

Solving Method on Airlift Loading Problem

ZHAO Hongfei1QI Yudong2SI Weichao2

(1. Equipment Department, No. 91395 Troops of PLA, Beijing 102443) (2. Department of Ordnance Science and Technology, Naval Aeronautical and Astronautical University, Yantai 264001)

The paper researched on the problem of airlift loading. It researched the problem mathematical model with multi-object and multi-carrier. And it established an algorithm of tabu neighborhood search with weight difference first, which can be used for solving the airlift loading optimization problem. The result showed that the algorithm can not only assure the target function not worse, but also reduce the search time and enhance the solving speed on the model.

airlift loading, multi-object, weight difference first, tabu search, optimization

2014年7月16日,

2014年8月26日

赵鸿飞,男,高级工程师,研究方向:装备保障。齐玉东,男,博士,教授,研究方向:指挥控制。司维超,男,博士,讲师,研究方向:指挥控制。

TP202

10.3969/j.issn1672-9730.2015.01.012