W(0，1)的李双代数结构

邵霞，付佳媛，祁杰

(中国传媒大学理工学部，北京 100024)

1 引言

Drinfeld于1983年基于量子群的基础首次引入李双代数的概念。量子群理论的核心部分是研究那些既非交换又非余交换的Hopf代数。

本文拟先研究W(0，1)的李双代数结构，确定其三角性与上边缘性。从而更易于我们对W(a，b)的李双代数结构的研究。

2 预备知识

首先，我们回顾一些与李双代数相关的一些基本定义及结果。

R 为复数域C 上的向量空间，ξ是 R⊗R⊗R 上的循环映射，即 ξ(x1⊗x2⊗x3)=x2⊗x3⊗x1，∀x1，x2，x3∈R，τ为 R⊗R 上的扭映射，即 τ(x⊗y)=y⊗x，∀x，y∈R。

R为复数域C上的向量空间，若存在线性映射σ:R⊗R→R满足:

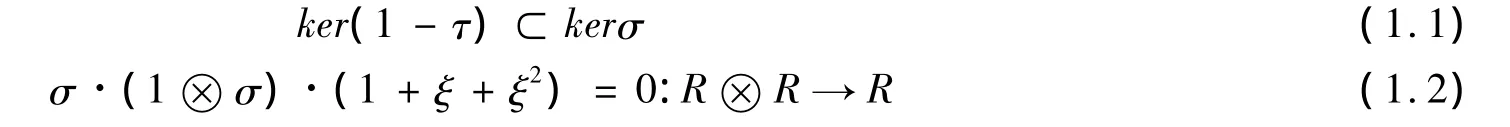
称(R，σ)是一个李代数。

R为复数域C上的向量空间，若存在线性映射:△R→R⊗R:满足:

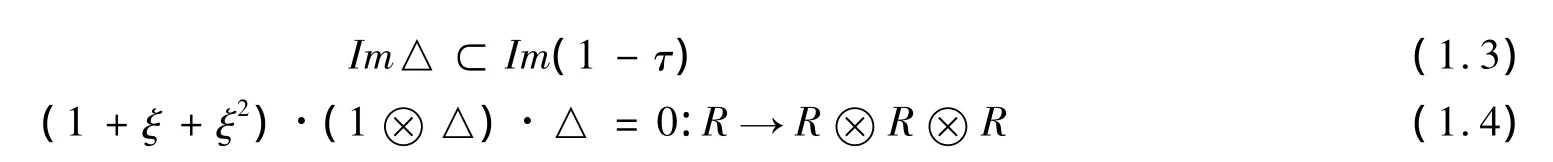
称(R，△)是李余代数。

对于李代数R，我们记［x，y］=σ(x，y)，用·表示伴随对角作用:

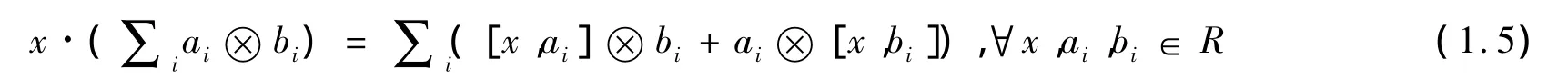
定义2.1 若(R，σ)是李代数，(R，△)是李余代数，且满足相容性条件:

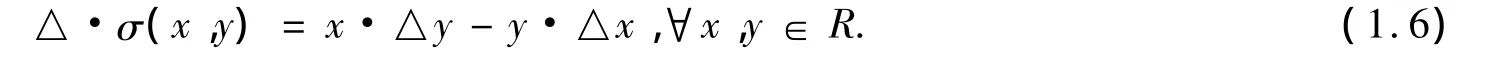
称三元对(R，σ，△)为李双代数。

U(R)是 R 中的普遍包络代数，1 是 U 中的单位元，对，定义 rij，c(r)，i，j=1，2，3

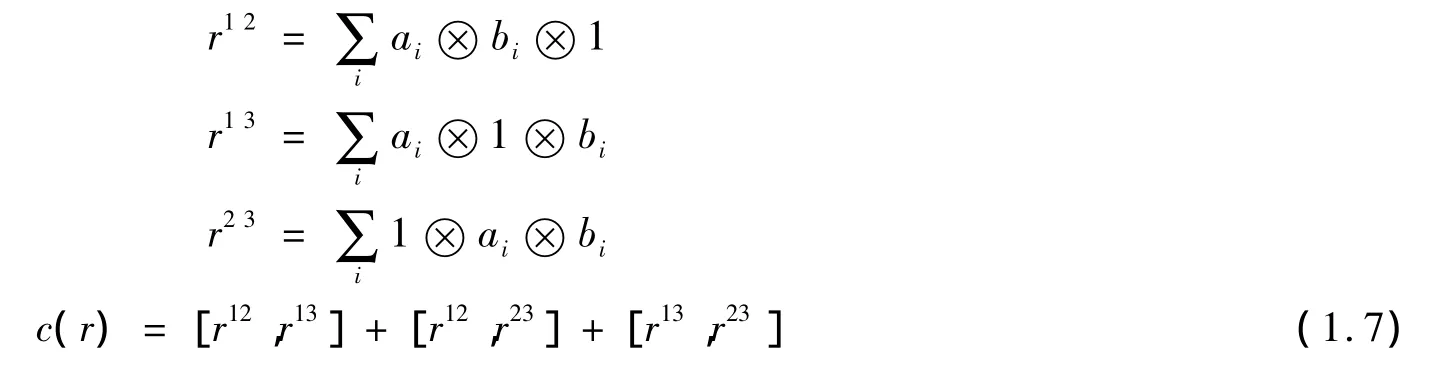
为U⊗U⊗U中的元素。

定义2.2 (1)四元对(R，σ，△，r)称作是一个上边缘的李双代数，如果(R，σ，△)是一个李双代数，r∈Im(1-τ)∈R⊗R使得△是r的一个三角上边缘，即:△=△r，且

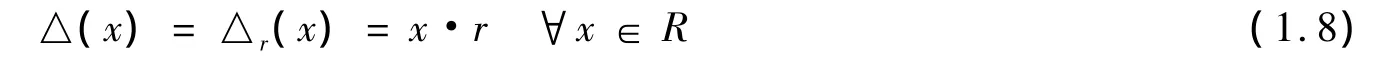
(2)上边缘李双代数(R，σ，△，r)称作是上三角的，如果r满足经典Yang-Batex方程(CYBE):

3 W(0，1)主要结果及其证明

首先，我们给出李代数W(0，1)的定义，复数域C上无限维李代数W(0，1)满足李括号积:

其中 i，j∈ℤ .为方便起见，以下均记 W(0，1).为 W

(1)三元对(R，［·，·］，△)是一个李双代数，当且仅当 r满足 CYBE.

(2)(1+ ξ+ ξ2)·(1⊗ △)·△(x)=x·c(r)，∀x∈ R (2.3)引理3.2 令W⊗n表示n个W的张量积，在W的伴随对角作用下，W⊗n称为一个R-模，假设r∈W⊗n满足x·r=0，∀x∈W.则 r∈C c⊗n。

元素r∈Im(1-τ)⊂W⊗W称为满足修正Yang-Batex方程(MYBE)，若

推论3.3 元素r∈Im(1-τ)⊂W⊗W 满足CYBE，当且仅当它满足MYBE.

V=W⊗W为在伴随对角作用下的W-模.记Der(W，V)为W到V的所有导子的集合，d:W→V，d是一个线性映射，满足:

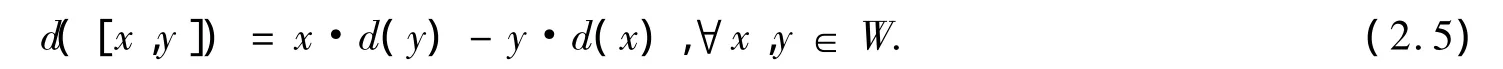
对∀v∈V，定义内导子vinn如下:

记Inn(W，V)为所有内导子的集合.我们知道

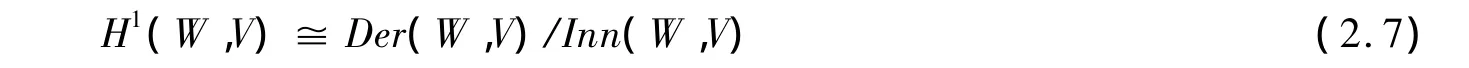
H1(W，V)为的系数在V中的一阶上同调群。

若d(Wn)⊂Wσ+n，n∈ℤ，称导子d∈Der(W，V)是一个次数为α的齐次导子，则

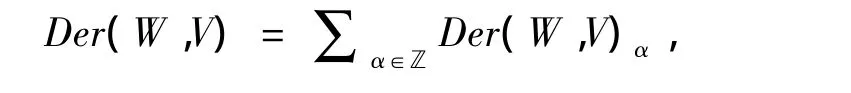
其中

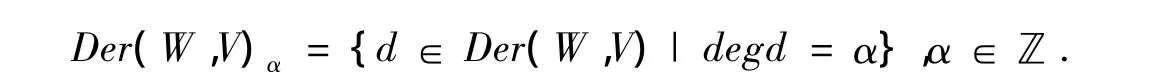
在下面意义下成立，对所有 u∈W，仅有有限多个 dα(u)≠0，d∈Der(W，V).(称 d=∑α∈ℤdα是可加的).

命题3.4Der(W，V)=Inn(W，V)，相应地，H1(W，V)=0。

只需证明每一个d∈Der(W，V)，d=∑α∈ℤdα是可加的，且这有限个dα均是W到V的内导子即可。

断言1 若0≠α∈ℤ则dα∈Inn(W，V)。

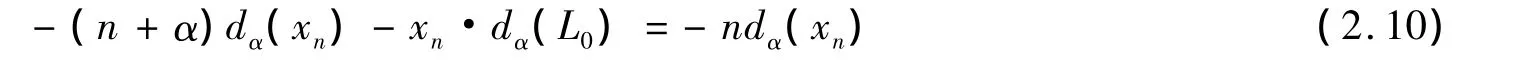
即 dα(xn)=uinn(xn).因此 dα=uinn是一个内导子。

以下，用“≡”表示一个等式在模C(c⊗c)作用下恒成立。

断言2 对 d0∈Der(W，V)0，有 d0∈Inn(W，V)。

下面我们分几个子断言来证明。

子断言1 d0(L0)≡d0(c)≡0

对∀xn∈Wn，n∈ℤ ，将 d0分别作用在［L0，xn］=-nxn，［xn，c］=0 的两边，有 xn·d0(L0)=xn·d0(c)=0。由引理3.2 得，d0(L0)≡d0(c)≡0。

子断言2 存在u∈V0，使得将d0用d0-uinn替换后有d0(W)≡0。

对∀0≠m∈ℤ，n∈ℤ设

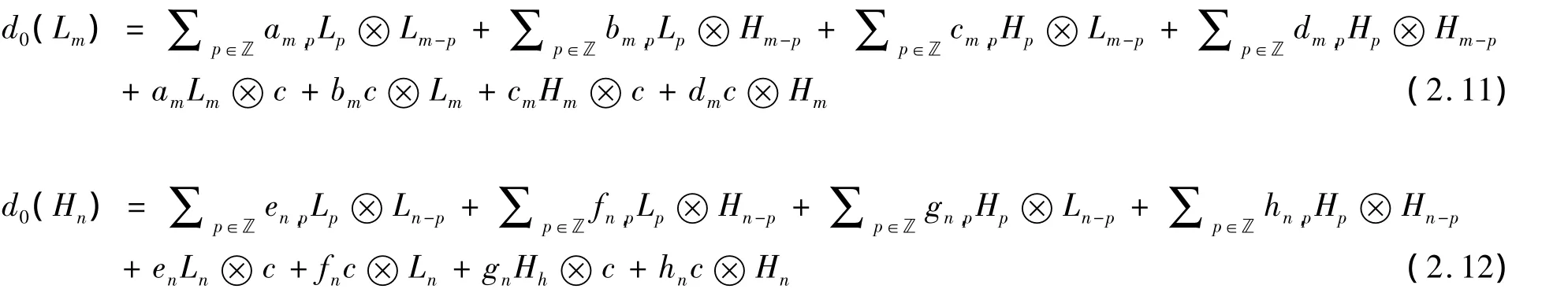
注意，对∀p∈ℤ，下面作用成立

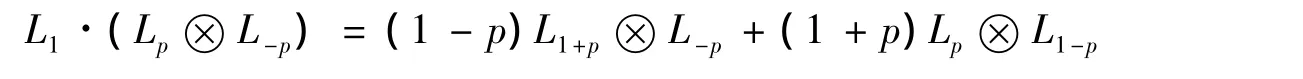
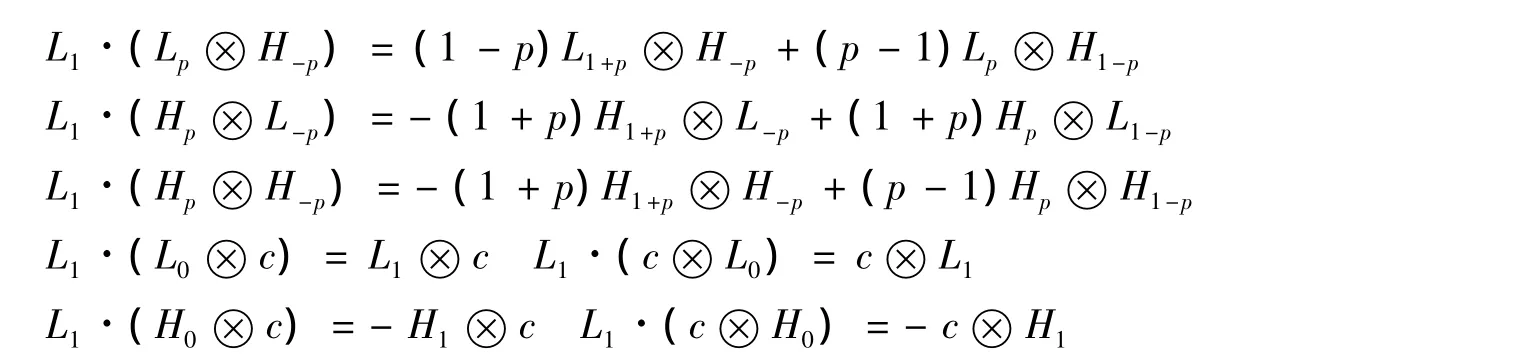
记

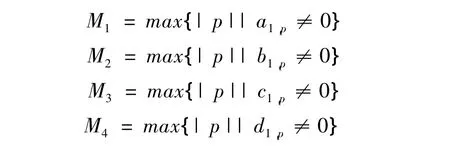
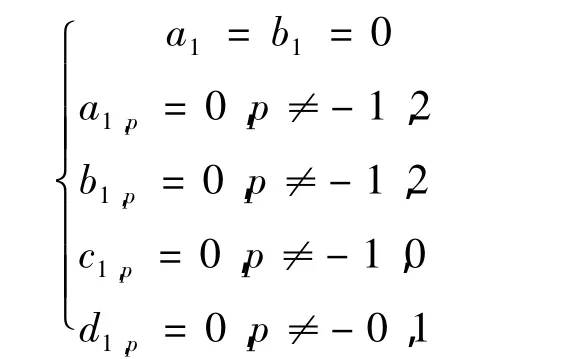
因此d0(L1)可以简化为

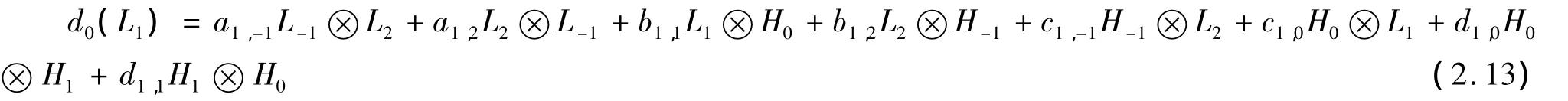
将 d0作用在等式［L-1，L1］=2L0两边，比较的系数推出

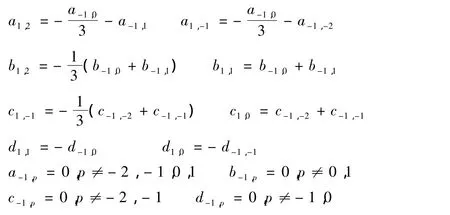
因此

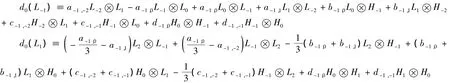
将 d0作用在等式［L2，L-1］=3L1两边，对∀p∈ℤ ，比较的系数有

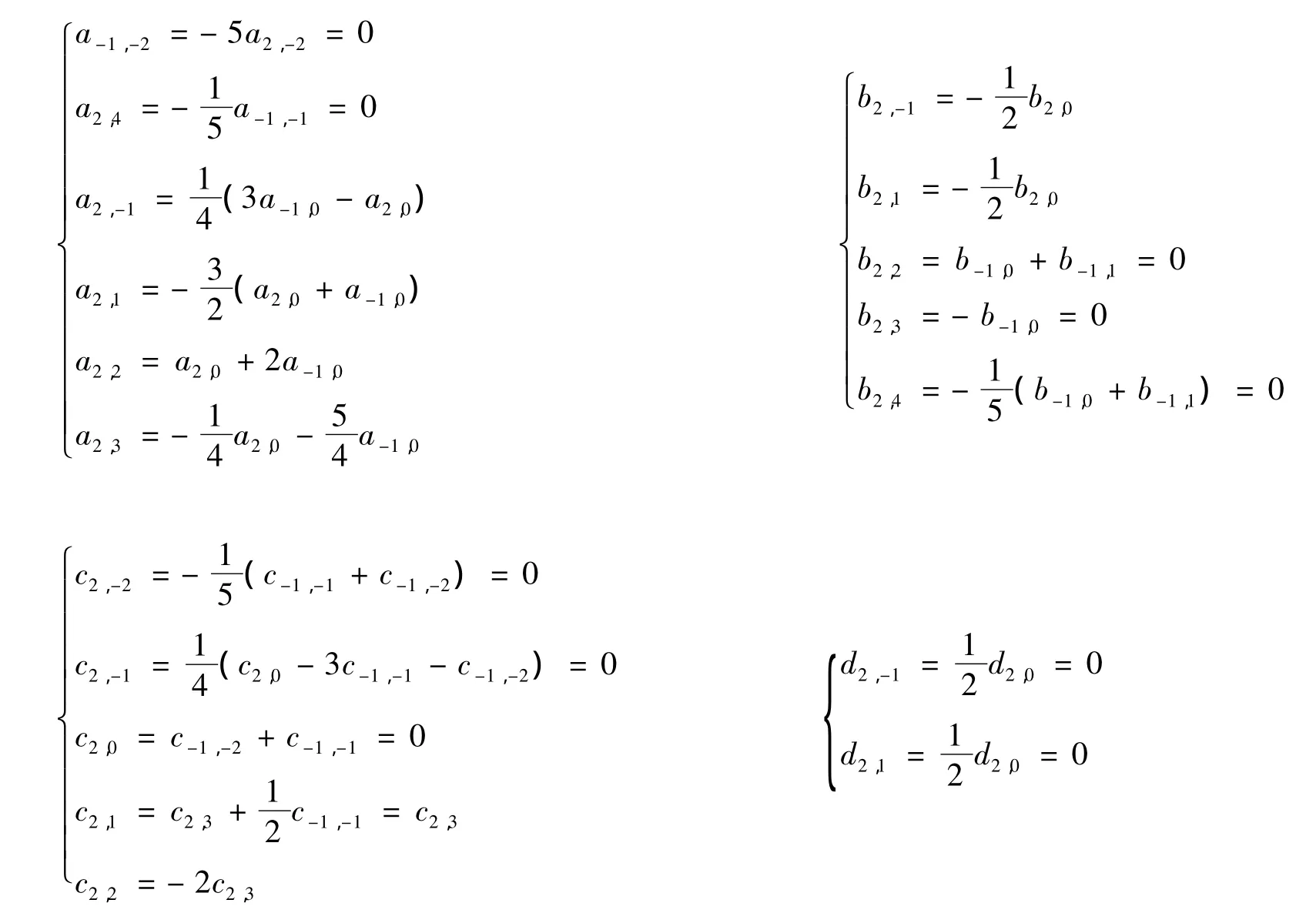
因此

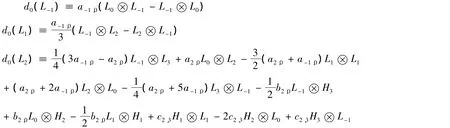
将 d0作用在等式［L1，L－2］ =3L－1的两边，对 ∀p ∈ ℤ ，比较的系数有

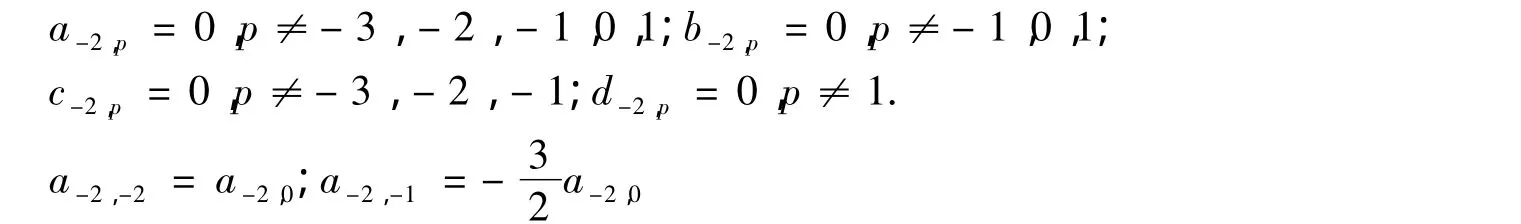
因此

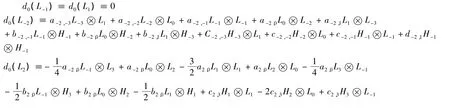
将d0作用在等式［L2，L-2］=4L0的两边，比较系数可得

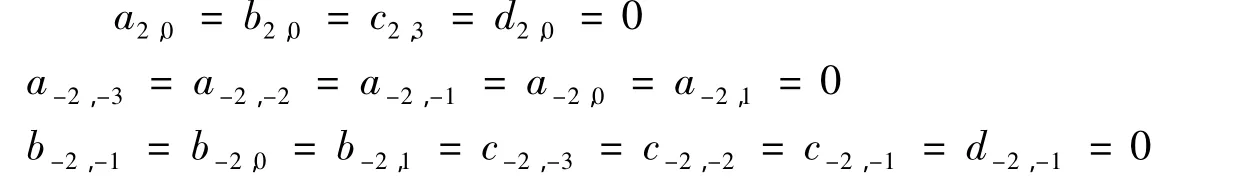
故

记 Vir是 W 的 Virasoro 子代数，即 Vir=spanC{Ln|n∈ℤ }可由基{L-2，L-1，L1，L2}生成.又由于(2.13)、(2.14)，可得

将 d0作用在等式［L0，［L0，H2］］=2H2的两边，比较系数可知

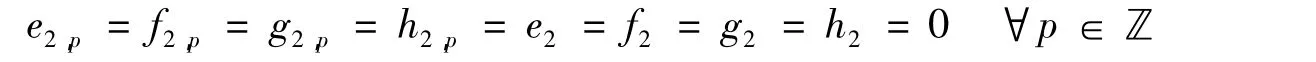
故

又由于 W 由{L-2，L-1，L2，H2}生成，由(2.15)、(2.16)可知

断言2得证。

断言3 d0≡0。

断言4 仅有有限多个n∈ℤ使dn≠0。

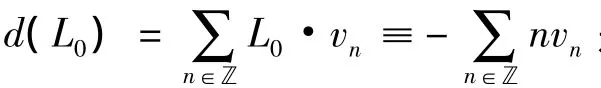
引理3.4 假设 ∃v∈V使对 ∀x∈W，x·v∈Im(1⊗1-τ)，则v∈Im(1⊗1-τ)。

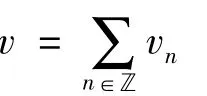
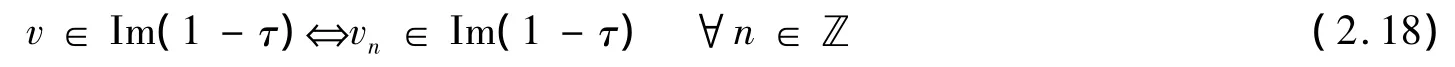
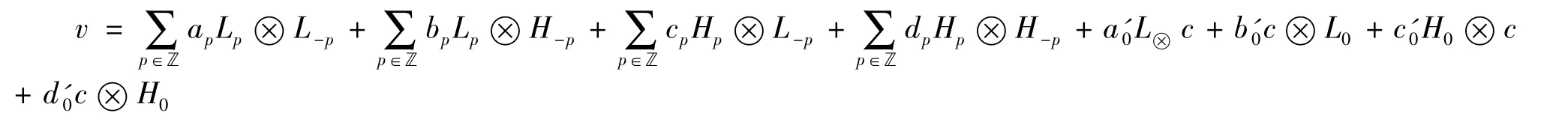
上述等式中的系数均在域C中，且每个求和符号对应的和式均为有限项求和，记元素都是 Im(1- τ)中的元素.用 v-u 代替 v，u 可以表示成 u1，p，u2，p，u3，p，u1，u2的线性组合，我们可以假设

则

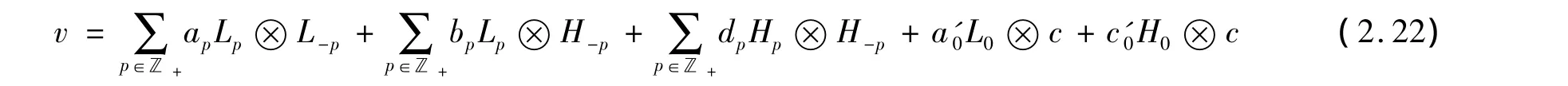
假设存在 p ＞0，使 ap≠0，取 q ＞0，使 q≠p，则 Lp+q⊗L-p是在 Lp·v中的项，然而，由(2.20)可知，L-p⊗Lp+q不是 Lq·v中的项，与 Lq·v∈Im(1-τ)矛盾;进一步假设 qp=0，∀p∈ℤ*(这里ℤ*表示非零整数)，类似地，同样可以假设dp=0，∀p∈ℤ*，因此(2.22)可表示为

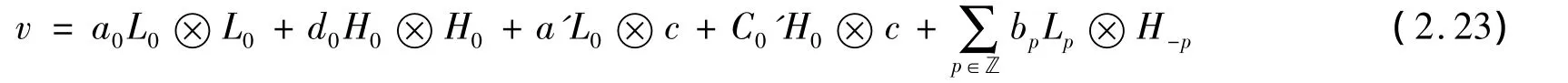
由Im(1-τ)⊂ker(1-τ)及我们的假设W·v⊂Im(1-τ)可以推出a0=d0=a'0=c'0=bp=0 ∀p∈ℤ，且我们有

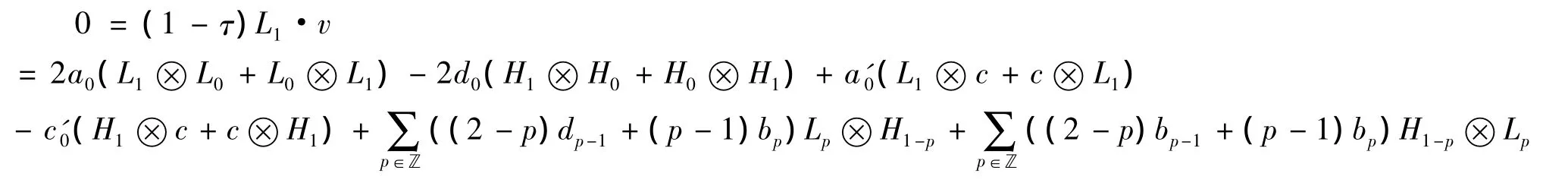
注意到{p|bp≠0}是有限项，比较各项系数，则

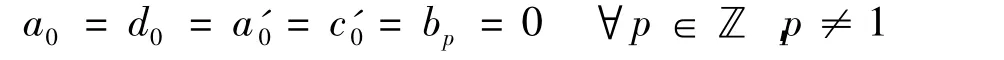
故(2.23)为

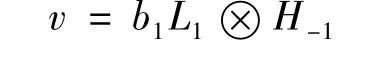
观察等式

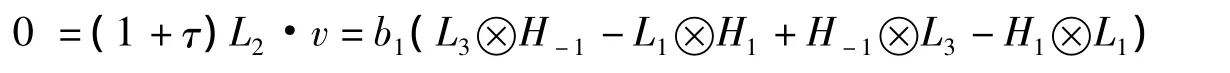
显然，b1=0.引理得证。

定理3.1 上的李双代数结构都是三角上边缘的。

设(W，［·，·］，△)是 W 上的一个李超双代数结构，由(1.6)、(2.5)及命题 3.4 可知，存在 r∈W⊗W，使得△ =△r，由于 Im△⊂Im(1-τ)及引理3.4 知，r∈Im(1-τ)，又由(1.4)、(2.3)及推论3.3，可知 c(r)=0.根据定义可知，(W，［·，·］，△)是一个上边缘的并且三角的李双代数。

［1］杨恒云.广义N=1，2超Virasoro代数的超双代数结构及表示［D］.上海交通大学，2008.

［2］J B Li，Y C Su.Lie bialgebra structures on the W-algebra W-(2，2)［J］.Math，arXiv:0801.4144，2008.

［3］J Z Han，J B Li，Y C Su.Lie bialgebra structures on the Schrödinger-Virasoro Lie algebra［J］.Math Phys，arX-iv:090.1339，2009.

［4］R Shen，H B Chen，J G Zhang.Lie bialgebra structures on generalized Heisenberg-Virasoro algebra［J］.Journal of Donghua University(Eng Ed)，2013，30(2).