基于模糊聚类模型的葡萄酒分类
2015-03-13魏舜洋石国良
魏舜洋,石国良
(中国传媒大学理工学部,北京 100024)
1 前言
葡萄酒是一种以新鲜的葡萄为原料,经酒精发酵制成的酒精含量不低于8.5%的饮料酒,是国际酒类中仅仅次于啤酒的第二大流行饮料酒[1]。葡萄酒中含有许多人体不可缺少的营养成分,如糖类,维生素,氨基酸,有机酸等。正是由于葡萄酒对人体的这些益处,葡萄酒消费量与日俱增。但是目前市场上的葡萄酒良莠不齐,人们也越来越关注葡萄酒质量的鉴定。而目前葡萄酒质量的鉴别主要是靠感官品尝和仪器分析来确定,但这两种方法都存在着缺陷。感官品尝需要专业的品酒师,一般人无法做到,借助液相色谱仪、原子吸收光谱、质谱分析仪等仪器分析程序比较复杂,使用的费用昂贵,且不能达到实际应用中实时、快捷的要求,因此这两种方法都不太适合大规模的使用。本文主要将模糊聚类的方法运用到了葡萄酒分类的鉴别中,对模糊聚类分析方法用于葡萄酒分类进行探讨。本文数据基于2012年全国大学生数学建模竞赛A题附件2所给的数据分析如何运用模糊聚类分析[2]的方法来根据酿酒葡萄的理化指标和葡萄酒的质量对这些酿酒葡萄进行分类。
2 基于模糊聚类分析葡萄酒的分类
2.1 模糊聚类分析
模糊聚类分析,又称为动态聚类法。当选定一批聚类中心时,其指标能够反映该类的特征,将样本向最近的聚类中心去聚类。再根据分类的结果来确定新的聚类中心,其各项指标就为该类中所有样本的相应指标的平均值。然后计算出前后两聚类中心的差异,比如差异大于某个值时,说明分类不合理,需要修改分类,即以新的聚类中心来代替旧的聚类中心,直到前后两聚类中心的差异小于某个值时,认为分类合理,从而停止分类过程。
2.2 数据预处理
本文所采用的数据基于2012年全国大学生数学建模竞赛A题附件2所给的数据,给出了红葡萄酒和白葡萄的酿酒葡萄的理化指标,而本文主要针对其中一种葡萄酒来研究模糊聚类分析在葡萄酒的分类中的应用。本文选择了红葡萄酒,其中有27个红葡萄酒样品,与之相联系有9个理化指标;将数据进行清洗和处理,得到数据见表1。
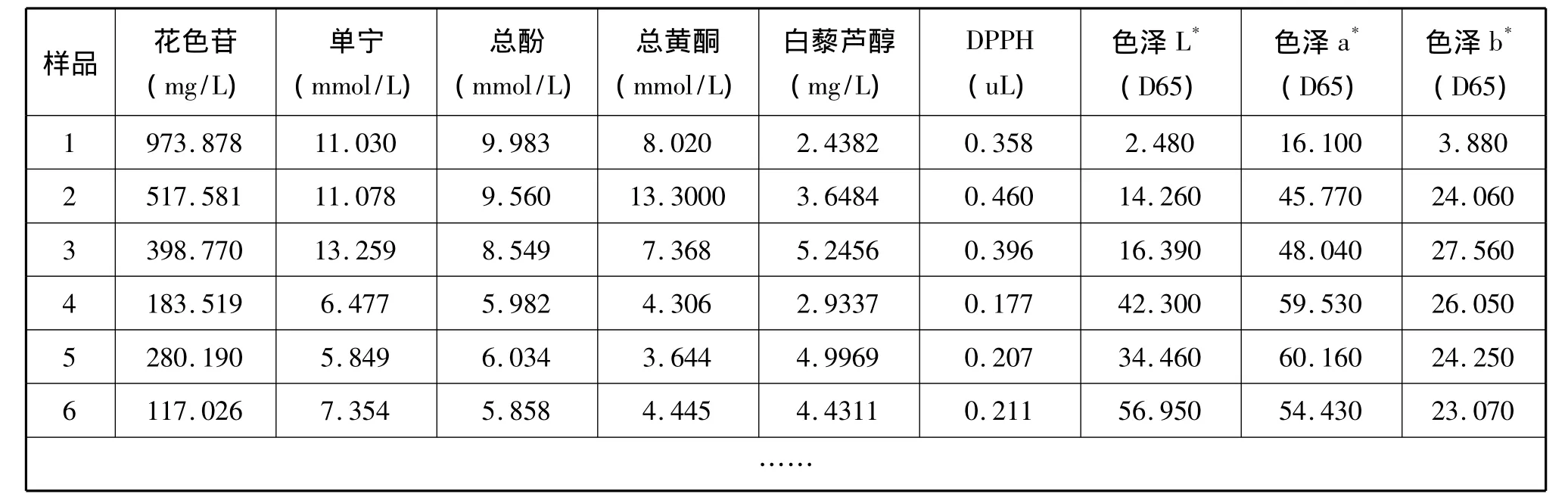
表1 红葡萄酒的理化指标(部分)
从表1,我们很容易发现这些酿酒葡萄的理化指标的单位不一致,即每个指标单位和数量级都存在着差异,我们就不能直接进行比较。若直接运用这些理化指标的数据进行分析,很可能会突出某些数量级大的指标在分类中的权重却忽视了数量级较小的特征性理化指标,导致了换一个单位就会将聚类结果推翻,得到不同的结果。所以,在聚类分析前,我们应该对这些数据进行量纲处理,这样每一种特征的理化指标值都会统一于一个具有可比较性的特定范围内。为了使不同的量纲的量也能进行比较,通常需要对数据作适当的变换。
2.3 聚类模型的建立
第一步:数据标准化
设论域 U={x1,x2,…,xn}为被分类的对象,每个对象又由m个指标表示其性状,即xi=(xi1,xi2,…,xim)(i=1,2,…,n),于是得到了原始数据矩阵为
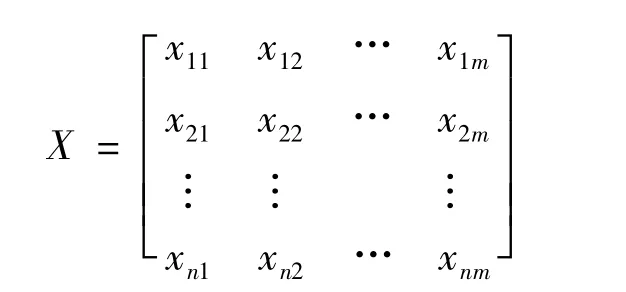
通常根据模糊矩阵的要求,运用数据标准化方法将数据压缩到区间[0,1]上[3]。样本的数据标准化方法有许多种,平移标准差变换、平移极差变换、对数变换等都是常用的数据处理方法。
本文采用的是平移极差变换,

设论域 U={x1,x2,…,xn},xi=(xi1,xi2,…,xim),建立模糊相似矩阵和xi与xj的相似程度rij=R(xi,xj)。相似关系R是衡量样本之间相似度的一种模糊度量的方法,是模糊相似矩阵。
直接距离法:rij=1 -cd(xi,xj),
其中 c为选取适当的参数,使得0≤rij≤1,d(xi,xj)表示xi与xj的距离。常采用的距离有海明(Hamming)距离、欧几里得(Euclid)距离、切比雪夫(Chebyshev)距离[4]等。
本文采用的是海明距离法,选取合适的常数c,使得 0≤rij≤1

将酿酒葡萄的理化指标数据通过一定的数理统计的方法进行预处理后,使它们具有统一的度量与可比性,可以通过以上模型的计算方法,把数据代入数据原始的矩阵,进行计算。
第三步:聚类(求动态聚类图)
由模糊相似矩阵R={rij}n×n构建模糊等价矩阵,根据公式,当U有限时,模糊相似矩阵R的传递闭包t(R)=Rk,(k>n)定是模糊等价矩阵 R*,因此,用平分法求:计算 R2=R·R,R4=R2·R2,…,直到 R2n=Rn=Rn,则 R*=Rn。
在模糊聚类中,并没有预先指定聚类数量,数据是根据自身的特征自动聚成不同类型的类。若输入不同的值,便会得到不同的聚类结果,这也是模糊聚类的特征。
3 模糊聚类分析的属性约简
3.1 酿酒葡萄与葡萄酒的理化指标的相关分析
相关分析[5]是研究变量之间相关关系的一种统计分析方法,它可以衡量两个变量之间的相关密切程度,数据(x1,y1),(x2,y2),…(xn,yn).

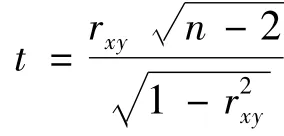
由于葡萄酒质量和酿就葡萄质量密切相关,因此对葡萄酒分类时要考虑与葡萄酒有显著相关的酿酒葡萄的理化指标。通过相关性分析可以找到与葡萄酒有显著相关的酿酒葡萄的理化指标,一方面,这些指标可以作为对葡萄酒分类的部分指标,另一方面,可以通过对酿酒葡萄的这些理化指标的检测控制酿葡萄酒原料的质量,从而可以从根源上提高葡萄酒的质量。
下面给出了相关分析的理化指标的部分相关系数表[6],如表2 所示。
我们从表2可以看出,红葡萄酒与酿酒葡萄的花色苷,DPPH,总酚,单宁,总黄酮,色泽a*均在水平下显著相关。其中色泽a*负相关,而红葡萄酒与酿酒葡萄的白藜芦醇、色泽L*及b*不相关。

表2 酿酒葡萄理化指标的相关性系数表
通过对酿酒葡萄与红葡萄酒的理化指标的相关性分析,从酿酒葡萄的理化指标中选出了与葡萄酒的理化指标有显著相关性的理化指标作为葡萄酒分类的部分指标,分别是:红葡萄酒的酿酒葡萄的理化指标有花色苷、单宁、总酚、总黄酮、DPPH、色泽a*。我们结合酿酒葡萄的这些显著相关性的理化指标重新对葡萄酒运用模糊聚类的方法进行分类。
3.2 酿酒葡萄理化指标的权重确定
由3.1节分析结果可知,各个指标对于酿制葡萄酒所起的作用是不一样的,因此本文基于属性的约简,确定了各个理化指标的权重[7],从而突出各个指标在分类过程中所占有的地位和所起的作用。实验验证,权重的确定影响着方案排序结果的可靠性和正确性。各理化指标的权重如表3所示。

表3 显著相关性理化指标的权重
4 实验结果及分析
基于模糊聚类分析的建模思想,将表1中的红葡萄酒的理化指标的数据写成数据矩阵。运用MATLAB软件,得到红葡萄酒分类动态聚类图,如图1所示。

图1 红葡萄酒的分类动态聚类图
从图1红葡萄酒分类的动态聚类图中,不难发现若将样品分成三类,有
第一类:{1,2},
第二类:{3,9,8,11,20,21,23},
第三类:{15,16,14,17,19,24,27,18,22,26,4,5,13,6,7,12,10}。
基于酿酒葡萄与葡萄酒的理化指标的相关分析,得出了与红葡萄酒有显著相关性的理化指标是花色苷、单宁、总酚、总黄酮、DPPH、色泽a*。将这些有显著相关性的理化指标重新写成数据矩阵,运用MATLAB软件,到红葡萄酒分类动态聚类图,如图2所示。
图2红葡萄酒分类的动态聚类图显示,若将样品分成三类,有
第一类:{1,8},

图2 红葡萄酒的分类动态聚类图
第二类:{2,23},
第三类:{24,26,25,27,22,6,17,14,15,10,16,13,19,12,10,16,13,19,12,18,4,6,20,21,3,9,11}。
基于酿酒葡萄理化指标权重的确定,每个理化指标都有相应的权重。将具有权重的酿酒葡萄的理化指标重新写成数据矩阵,运用MATLAB软件,得到红葡萄酒分类动态聚类图,如图3所示。
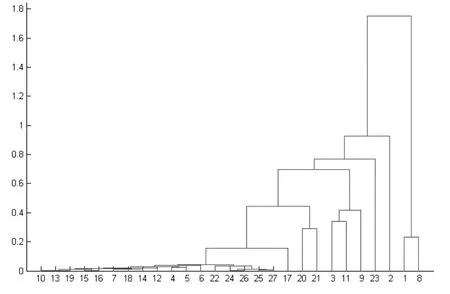
图3 红葡萄酒的分类动态聚类图
图3红葡萄酒分类的动态聚类图显示,若将样品分成三类,有
第一类:{1,8},
第二类:{2},
第三类:
{23,24,26,25,27,22,6,17,14,15,10,16,13,19,12,10,16,13,19,12,18,4,6,20,21,3,9,11}。
文献[2]中采用的是系统聚类法,分类的结果如下:
第一类:{1},
第二类:{2,8,9},
第三类:{3,4,5,6,7,10,11,12,13,14,15,16,17,18,19,20,21,22,23,24,25,26,27}。
从以上的聚类效果可知,样品8的类别是存在歧义的,进一步分析酿酒葡萄的理化指标可知,与样品2的指标数据相比,样品1的各指标与样品8更为接近,因此将样品1和样品8归为一类者似乎更为合理,这就验证了基于模糊聚类模型的有效性和实用性。
另外,由于模糊聚类分析具有动态的特征,比较以上实验结果发现:将27个样品分为四类时图2和图3显示的结果一致。分类结果如下:
第一类:{1,8},
第二类:{2},
第三类:{23},
第四类:
{24,26,25,27,22,6,17,14,15,10,16,13,19,12,10,16,13,19,12,18,4,6,20,21,3,9,11}。
显然分成四类结果与三类的结果相同之处在与样品1、样品2、样品8始终属于离散类别(类别包含样品较少称为离散类别),不同之处就在于样品23是否也为离散类别。根据酿葡萄酒的理化指标数据显示,与普通类别(类别包含样品数目较多称为普通类别)有明显差异,因而我们认为此时分类效果更优。
5 总结
本文主要将模糊聚类分析的思想和方法运用到了市场上良莠不齐的葡萄酒质量鉴定分类中,建立了葡萄酒分类的模糊聚类分析模型。本文采用了相关性分析进行属性约简并且用相关性系数作为各个理化指标的权重,也可以运用粗糙集的相关理论进行属性约简,对于权重的确定也可采用基于粗糙集条件信息熵的权重确定,这些将在以后的工作中进一步讨论。
[1]高景山.基于人工鱼群的模糊聚类算法研究及其在葡萄酒分类中的应用[D].西安:长安大学硕士论文,2013.
[2]Kanade P.Fuzzy ants as a clustering concept[D].M S diassertation,University of South Florida,Tampa,FL,2004.
[3]谢季坚,刘承平.模糊数学方法及其应用(第3版)[M].武汉:华中科技大学出版,2006.
[4]Nascimento S,Mirkin B,Moura -Pires F.Modeling proportional membership in fuzzy clustering[J].IEEE Transcations on fuzzy Systerms,2003,11(2):173-186.
[5]茆诗松,程依明.概率论与数理统计[M].北京:高等教育出版社,2011.
[6]霍明娟.基于聚类分析法的葡萄酒评价[J].太原师范学院学报(自然科学版),2014,13(2):35-4.
[7]韩小孩,张耀辉.基于主成分分析的指标权重确定方法[J].四川兵工学报,2012,10(33):124 -126.
