高温应变接触式测量精度影响因素研究

王文瑞，张佳明，聂 帅

(北京科技大学 机械工程学院，北京 100083)



高温应变接触式测量精度影响因素研究

王文瑞，张佳明，聂 帅

(北京科技大学 机械工程学院，北京 100083)

高温结构热强度、热疲劳等问题的研究需要高温应变的精准测量。利用自主研制的自由框架丝栅式高温应变片开展结构高温应变测量精度影响因素研究，结合应变片结构与测量原理，建立高温应变片应变信息传递以及分布有限元模型，分析对比被测构件与敏感栅丝表面应变场的分布情况，确定高温应变片尺寸参数与使用参数对应变测量精度的影响因素，为应变片的设计与使用提供依据。提出了合适的丝栅式应变片结构参数，并利用高温应变片实验进行验证，确定了高温接触式应变测量精度影响因素，降低环节敏感性，提高高温应变测量精度，并可为其他形式的应变片的测量精度研究提供依据。

自由框架丝栅式高温应变片；测量精度；影响因素；应变分布；敏感栅

0 引言

高温环境中结构的强度、寿命及可靠性等直接影响结构安全性，而这些大都与结构的应变变形破坏相关[1]。目前，高温结构的应变行为发生改变，形成热强度、热疲劳等与机械强度耦合的问题，热弹塑性理论对一般平面问题还不能完全解决，复杂高温结构的工程热力耦合问题更是束手无策[2]。通过结构的高温应变测量等实验手段来研究结构高温热力变形行为就成为必须。高温结构应变的精准测量方法也是当前国内外科研工作者迫切需要解决的难点[3]。

基于应变电测原理的高温应变接触式测量方法，可靠性高，适应性好，一直是高温应变测量的主要途径[4]。但由于高温环境的影响，应变片的指示应变往往与实际相差甚远，甚至不能确定指示应变曲线的真实性[1,5]。究其原因，接触式高温应变测量结果精度及其影响因素系统研究一直是高温应变测量的薄弱环节[6]。

本文利用自主研制的自由框架丝栅式高温应变片，开展结构高温应变测量精度影响因素仿真与实验。结合应变片结构原理，建立高温应变片应变信息传递及分布有限元测量模型，确定高温应变片尺寸参数与使用参数对应变测量精度的影响关系，并通过实验验证仿真结果，为应变片的设计与使用提供依据。

1 自由框架丝栅式高温应变片测量原理

常温应变片为箔式结构，无法用于高温(300 ℃以上)应变测量，高温应变片通常设计为丝栅式结构[7]。针对接触式高温应变测量，课题组研制了具有自主知识产权的自由框架丝栅式高温应变片，如图1所示。该应变片由临时基底、敏感丝栅与引线等组成。使用时，剔除临时基底，将应变敏感丝栅固定在被测构件上。

图1 自由框架丝栅式高温应变片

目前设计的自由框架丝栅式高温应变片体积小，分散度低，具有良好的电阻温敏系数，可对室温～1 000 ℃的构件应变进行测量。

被测表面发生形变时，构件表面应变转化为应变片电阻的变化，按照物理学可知应变片电阻为

(1)

式中R为应变片金属丝的电阻；ρ为应变片金属丝的电阻率；L为应变片金属丝的长度；A为应变片金属丝的截面积。

当应变片随构件变形时，其电阻值发生变化，即对式(1)求微积分：

(2)

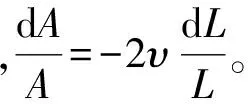
(3)

据高压下金属丝性能研究可知：

式中m为比例系数，一般为常数。

(4)

即

(5)

式中ε为应变片的应变值；K为敏感栅材料灵敏度系数。

这样，由于应变片电阻变化，通过整流电桥，输出易于测量的电压信号，最终转换为结构应变。

2 高温应变片测量模型

为建立高温应变测量模型，本文搭建了图2(a)所示高温应变测量系统的加载装置。加载装置采用简支等应变梁作为研究对象，实验中将砝码加载到简支梁上，产生机械应变值，以及由于环境高温在梁表面产生的热应变值，共同构成测量的真实应变。高温应变片通过无机磷酸盐胶固定在构件表面，胶层将简支梁表面的变形传递给敏感栅，敏感栅因此输出指示应变。由于胶层、丝栅结构等参数的影响，指示应变与真实应变并不一致。习惯上，把指示应变与真实应变的差异称为测量误差[8]。

由图2(b)及材料力学公式可知简支梁中点处挠度：

(6)

其中，F=G/2。

简支梁中间等应变段的弯矩为

M=FRA·x-F(x-a1)=Fa1

(7)

根据应力应变公式，中间段的应变为

(8)

由式(6)、式(8)可得

(9)

式中h为简支梁的厚度；ω为简支梁中间位置产生的挠度；l为简支梁有效段的长度；a1为力的加载位置到同侧支撑点的距离。

在实际测量时可根据加载装置中的千分表测量简支梁中点处的挠度值，根据式(9)直接计算出简支梁表面的实际应变。

(a) 测量系统加载装置

(b) 简支梁力学模型

根据图2力学模型，在ABAQUS有限元软件中建立有限元模型，由简支梁、胶层、敏感栅3部分组成，使用绑定约束将三者粘接在一起，如图3所示。

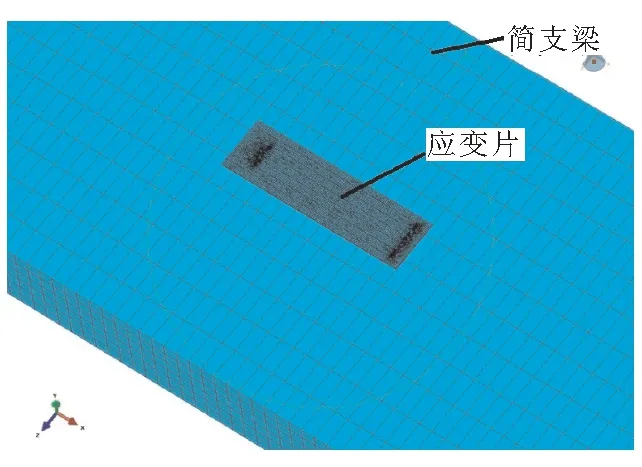
(a) 简支梁与应变片模型图

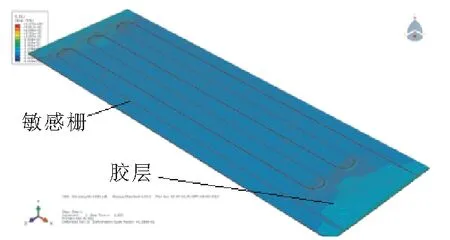
(b) 应变片模型局部放大图

本文通过材料力学理论计算与实验贴片测量的方式对有限元仿真结果进行验证，如表1所示。3种方式得到的简支梁表面应变值与中点挠度值相差不超过1%，表明本文建立的有限元模型正确，研究方法可行。

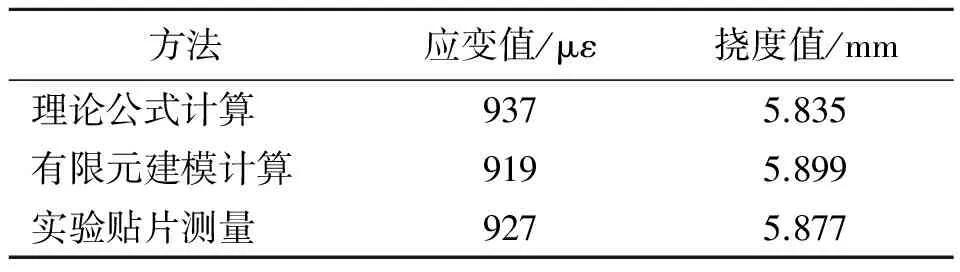
表1 不同方式得到的简支梁应变值、挠度值对比表

3 敏感栅尺寸对应变测量精度的影响

敏感栅的尺度直接影响应变测量结果的准确性，其主要尺寸参数包括栅丝直径、纵向栅丝长度和栅丝间距，如图4所示。

图4 敏感栅结构图

3.1 敏感栅直径对应变测量精度的影响

在有限元模型中，改变栅丝直径进行仿真，选取敏感栅有效段轴向分布的节点，输出应变值，得到敏感栅轴向应变分布随尺寸变化情况。

如图5所示，敏感栅测量应变是对整体所受应变的综合反映。尽管直径0.04 mm敏感栅所受应变的峰值较大，但其两端边降效应明显。敏感栅越细，越能够均匀且准确地反应被测构件表面的变形，测量误差也就越小。

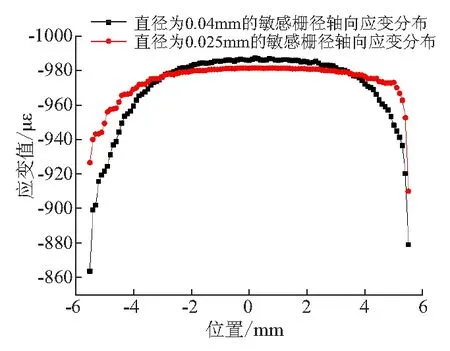
图5 不同直径敏感栅轴线方向应变分布情况

将应变片敏感栅应变与简支梁上对应点的应变值进行对比，得到应变结果的相对误差为

(10)

二者应变相对误差见图6，敏感栅越细所受应变越接近真实应变值，测量误差越小，当敏感栅直径由0.04 mm减小到0.02 mm时，应变测量误差可减小1.93%。

图6 应变测量误差随敏感栅直径的变化曲线

此外，根据实际应用可知，栅丝直径过小，会导致栅丝高温强度变差，发生断裂；直径过大，又会使得应变感应不够灵敏。一般地，应变片敏感栅丝直径为0.025～0.035 mm，受敏感栅丝拉拔工艺所限，最小直径为0.025 mm。

3.2 敏感栅长度对应变测量精度的影响

测量时敏感栅的栅长沿被测构件主应变方向布置，敏感栅的输出应变就是应变片总应变的主要部分。因此，应变片敏感栅的长度尺寸会影响测量的误差，决定了应变片测量的精度[9]。

图7为栅丝轴向应变分布，可知，敏感栅长度为6.5 mm时轴向应变分布最为均匀、平直，到了后1/3段有小幅下降。当敏感栅较长时，边降效应非常明显；当敏感栅较短时，所受应变整体较小且有明显的下降趋势，产生较大的测量误差。

图7 不同长度敏感栅轴线方向应变分布

以0.5 mm为间距对栅长2～10 mm的应变片模型进行仿真计算，敏感栅长度6.5 mm时测量误差为1.34%，敏感栅过长或过短都会影响敏感栅随被测构件的变形，使应变测量误差变大。如图8可知，其变化规律与800 ℃时的实际应变测量误差结果趋势一致，故取敏感栅长度为6.5 mm，此时应变片灵敏度系数也最大，可提高测量的精度。

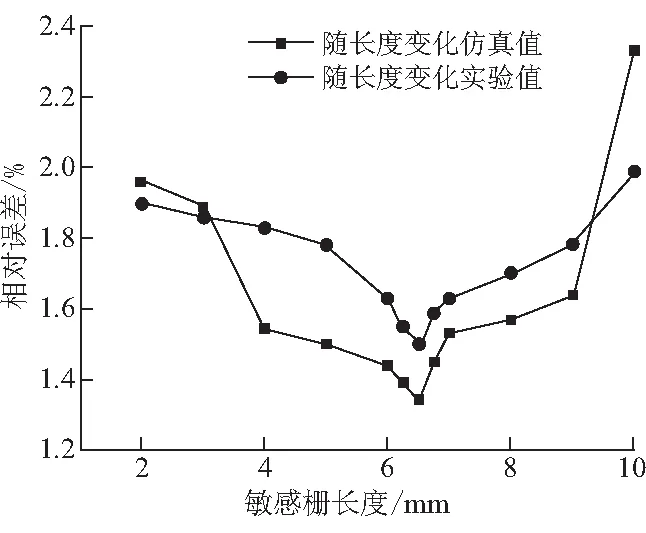
图8 应变测量误差随敏感栅长度变化曲线

3.3 敏感栅间距对应变测量精度的影响

栅间距的改变会影响胶层的应力应变分布情况以及应变片横向效应[10-12]，改变应变片敏感栅的应变输出值，影响应变测量误差。

由图9栅丝轴向应变分布可知，敏感栅间距变化时，其应变分布规律不变，但0.4 mm间距的敏感栅比其他尺寸敏感栅整体所受应变值略大，测量误差最小。

图9 不同间距敏感栅轴线方向应变分布

对栅丝间距为0.1～0.6 mm的有限元模型进行仿真计算，敏感栅间距0.4 mm时应变测量误差为1.16%，间距增大或减小都会增大应变测量误差。如图10所示，实验得到了与仿真相同的变化规律，0.4 mm为测量误差最小值对应的敏感栅间距。

图10 应变测量误差随敏感栅间距的变化曲线

4 胶层厚度对应变测量精度的影响

如前所述，真实应变到指示应变的过程，是应变经过胶层传递的物理过程，胶层特性成为实际应变分析的一重要因素[13]。目前，对应变片输出性能的研究，很少针对应变与粘结剂使用的关系[14-15]。然而，胶层却是高温应变测量精度的重要影响因素之一。

在实际使用中，测得胶层厚度一般在0.1～0.5 mm。仿真模型中，改变模型胶层厚度进行计算，如图11所示。

图11 应变片测量误差随胶层厚度的变化曲线

由图11可见，当胶层厚度从0.02 mm增大到0.5 mm时，敏感栅指示应变与简支梁被测应变之间相对误差增大了23.3%，胶层厚度越小应变测量误差也就越小。但厚度过小又会降低胶层在高温下的粘接强度以及绝缘电阻，影响测试信号的准确度。实验测量，发现当胶层厚度小于0.1 mm时绝缘电阻过小，不能用于测量。综合以上两方面因素，选择胶层厚度为0.1 mm。同时，仿真结果得到了实验测量的验证，得到了与仿真相同的变化规律。

应变测量过程中应变由胶层传递到敏感栅的过程中，应变损失的机理仍不清楚。本文对胶层内部应变情况进行研究，如图12(a)所示，将胶层沿厚度方向切分开，分析胶层内部应变场变化情况。

观察发现沿胶层厚度方向应变变化并不明显，且胶层底部节点就与简支梁表面有30 με左右的误差。并且简支梁表面粘贴胶层区域的应变场发生了明显变化，如图12(b)所示。

(a) 胶层内部应变场云图

(b) 简支梁表面应变分布云图

由于胶层具有一定刚度，对粘贴表面产生了局部强化作用，影响了被测构件表面应变场。为了验证这一推测，在有限元模型中改变胶层材料的弹性模量，得到不同弹性模量的胶层对简支梁表面应变场分布的影响规律，如图13所示，在胶层边界位置简支梁表面应变有突变发生，且粘贴应变片区域的应变值小于理论值1 000 με，两端应变下降明显，找到了边降效应的原因。胶层的弹性模量减小时，简支梁表面应变增大，误差也就随之减小。

图13 被测构件表面应变场分布随胶层弹性模量变化规律

5 实验验证

如图14所示，本章对高温应变片影响因素进行实验研究。使用上文得到的接触式高温应变测量的最优参数：敏感栅直径0.025 mm，长度6.5 mm，间距0.4 mm，胶层厚度0.1 mm，在800 ℃实验装置中下开展应变测试实验，测试数据见表2。

图14 应变测量实验图

温度/℃加载次数测量值/με真实值/με误差/%平均误差/%80011121100012．121142100014．231133100013．313．2

通过对接触式高温应变测量精度影响因素的分析与优化，得到800 ℃时的平均应变测量误差为13.2%，有效提高了高温应变测量精度。

6 结论

(1)通过建立高温应变片应变信息传递以及分布有限元测量模型，得到应变测量精度与应变场分布情况随各影响因素的变化规律。结果表明，敏感栅越细测量精度越高；高温应变片的敏感栅间距与长度具有精度最优值；固定胶层厚度越小、弹性模量越低测量精度也会明显提升。

(2)仿真分析结果得到了高温应变测量实验的验证，以此为依据对高温应变测量影响因素的参数优化，得到各影响因素的最优值。优化后800 ℃时的测量精度提高到13.2%，有效减小了应变测量误差，为应变片的设计与使用提供依据。证明了本文的研究方法可行，模型正确，可推广到其他形式的高温应变测量中。

[1] 尹福炎.箔式应变片结构模型与有限元分析[J].外文翻译，2009,38(5):47-50.

[2] Rohrbach C, Lexow J. Miniature force transducers with strain gauges[J]. Measurement,1986,4(3)：93-100.

[3] Mittmann H U, Czaika N, Czichos H. A new device for simultaneous measurement of friction force, normal force and friction coefficient[J]. Wear,1975,31(1):179-184.

[4] 尹福炎.瞬态加热条件下高温应变计测量误差的修正方法[J].强度与环境,2005(1):36-38.

[5] 吴东, 陈德江, 张松贺, 等. 高超声速飞行器典型部位高温应变测量[J]. 导弹与航天运载技术, 2012 (6): 30-33.

[6] 王欣, 姜常玖, 惠守江, 等. 无机胶植筋式后锚固连接的抗火性能研究[J]. 四川大学学报 (工程科学版), 2013,50(4): 27-33.

[7] 叶迎西，孙天贺，艾延延.温度对电阻应变片测量精度影响的仿真研究[J].沈阳航空航天大学学报,2013,30(2):27-31.

[8] 中国人民共和国国家质量监督检验检疫总局. GB/T13992—2010金属粘贴式电阻应变计[S].北京：中国标准出版社,2010.

[9] 郭弦，于飞，鲁辉.应变片栅长对混凝土表面静态应变测量结果的影响分析[J].电子测量技术,2010,33(1):89-91.

[10] 易晖，张卫.应变片横向效应对应变测量的影响与修正[J].直升机技术,2011,1:60-63.

[11] 李鹏，黄晴.测量中应变片的误差分析[J].企业家天地,2008,6:262-263.

[12] 庄重，张娜.电阻应变测试中横向效应误差分析[J].基础科学,2010,11:160-161.

[13] 尹福炎.电阻应变片与应变传递原理研究[J].科技应用,2010,39(2):1-8.

[14] 郑秀瑗，谢大吉.应力应变电测技术[M].北京：国防工业出版社,2002.

[15] 雷一鸣.电阻应变计应变传递研究及误差分析[J].科学技术与工程,2011,11(32):8096-8100.

(编辑：吕耀辉)

Simulation and experiment on influence factor of contact high temperature strain measurement accuracy

WANG Wen-rui, ZHANG Jia-ming, NIE Shuai

(School of Mechanical Engineering, University of Science and Technology Beijing, Beijing 100083, China)

The research of thermal strength and fatigue of high temperature structure needs high temperature strain measurement. The influence factor of high temperature strain was studied on the basis of independently developed high temperature free frame wire strain gauges. The strain transmission and distribution model was established according to the structure and measuring principle of high temperature strain gauge. The influence of size parameters and using parameters on strain measurement accuracy was obtained by the comparison between the strain fields of tested structure and sensitive gate, which provides the basis of design and utilization of strain gauge. The proper structural parameters were proposed in this paper which is verified by the high temperature strain measuring experiment. The precision influence factor of contact high temperature strain measurement was determined to lower the factor sensitivity and improve the precision of high temperature strain measurement, which provides a basis to perform measuring precision research of other forms of strain gauges.

high temperature free frame wire strain gauge；measuring precision；influence factor；strain distribution；sensitive gate

2014-05-13；

2014-10-10。

北京市高校青年英才计划 (YETP0368)；国家重大科学仪器设备开发专项(2011YQ14014507)。

王文瑞(1979—)，男，副教授，研究方向为高温材料、构件变形应变检测。E-mail:gmbitwrw@ustb.edu.cn

V416

A

1006-2793(2015)03-0439-06

10.7673/j.issn.1006-2793.2015.03.027