地球临边观测卫星的姿态角仿真分析方法

朱永生 胡海鹰 郑珍珍 苏瑞丰 张科科

(上海微小卫星工程中心， 上海 201203)



地球临边观测卫星的姿态角仿真分析方法

朱永生 胡海鹰 郑珍珍 苏瑞丰 张科科

(上海微小卫星工程中心， 上海 201203)

针对地球临边观测卫星的姿态角计算问题，给出一种应用STK软件进行仿真的分析方法。利用STK软件的连接接口联立STK软件，创建仿真场景；在二体模型下，求得临边观测卫星姿态角的解析解，并作为下一步精确迭代求解的初值；在WGS84地球模型下，调用STK软件中的高精度轨道外推模型(HPOP)，并结合推导的迭代公式，求得卫星姿态的高精度数值解。以20 km和100 km的临边观测为例，仿真计算姿态角，并将计算结果与二体模型方法的进行对比。结果表明，文章提出的方法可有效解决地球临边观测卫星的姿态角计算问题，且具有收敛迅速和计算精度高的优势。

地球临边观测；卫星姿态角；高精度计算

1 引言

地球临边观测是指利用卫星遥感器对准地球某一特定高度大气的切线方向进行观测，获得观测视场内一个大气层条带里的散射辐射，并配合扫描对所要观测大气的高度进行覆盖探测。临边观测是地球大气探测的主要方式之一，由于其空间覆盖范围大、垂直分辨率高且无需特定目标辅助，近来受到越来越多关注[1-3]。进行临边观测时，卫星一般通过姿态机动使遥感器指向不同高度大气的切线方向，因此卫星的姿态角计算是临边观测必须要解决的问题。然而，卫星运动复杂[4-6]，且地球形状不规则[7]，使姿态角的精确计算成为一个难点。

目前，地球临边观测卫星的姿态角计算，主要是假设地球为理想球形的二体模型，即使考虑了地球扁率摄动等对卫星运动的影响，在计算姿态角时仍要认为地球半径一致[8-9]。这种方法虽然计算简单，但是计算精度差。本文充分利用STK软件中的高精度轨道外推(HPOP)模型[10]和WGS84地球模型，结合MATLAB软件的编程计算能力，提出了地球临边观测卫星姿态角[11]的仿真分析方法。该方法可求出高精度数值解[12]，从而解决利用临边观测切点高度求解卫星姿态角问题，为临边观测卫星姿态控制提供参考目标；还可应用于有探测结果时，对应时间和姿态角测量值计算出探测高度。

2 动力学建模及方法设计

2.1 运动方程

假设近地卫星飞行过程中只受到地球引力作用，且地球是半径Re为6 378.137 km的球体(理想情况)，则在二体模型下描述卫星的运动方程为

(1)

式中：r为卫星位置矢量；r为卫星地心距；μ为地球引力常数。

求解式(1)，可得

(2)

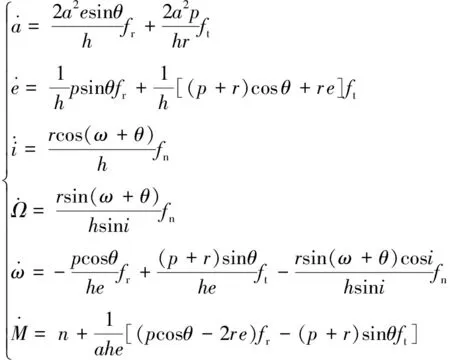
(3)

式中：a为轨道半长轴；i为轨道倾角；Ω为升交点赤经；ω为近地点幅角；M为平近点角；fr，ft，fn分别为径向、横向和法向摄动加速度；p为半通径。

2.2 临边观测模型

地球临边观测三维示意如图1所示。假设卫星初始姿态对地定向，遥感器视轴方向沿本体坐标系+yB轴，则通过调整卫星姿态滚动角便可调整临边观测高度，二维示意如图2所示。其中：P1为在地球为理想球形假设下，遥感器视轴与任务要求观测高度Δh处大气的切点，对应的姿态滚动角为φ1，与地心的距离为r1；P2为地球模型选择WGS84模型时，遥感器视轴与任务要求观测高度Δh处大气的切点，对应的姿态滚动角为φ2，与地心的距离为r2。

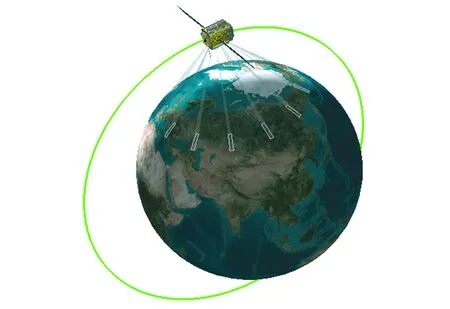
图1 临边观测三维示意Fig.1 3-D view of limb observation

由图2可知，临边观测卫星姿态滚动角同任务要求观测高度存在如下关系，可用来求得φ1和φ2。

(4)

式中：φ为姿态滚动角。

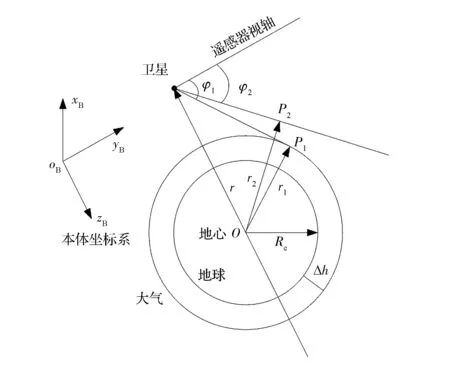
图2 临边观测二维示意Fig.2 2-D view of limb observation

另外，结合图1和图2还可以看出：卫星绕zB轴转动，设置不同的偏航角，可以观测不同地理位置的大气，但对观测大气的高度影响不大。因此，本文在分析地球临边观测卫星的姿态角时，只考虑滚动角，不考虑偏航角。

在大数据背景下，一个强大的智能平台是支撑网站急需前行的关键。目前，基于大数据技术的智能平台有许多，比如智能搜索引擎、智能化交互共享平台等。因此，大数据背景下的高校图书馆也需依靠智能平台为其各项服务提供支持，利用云计算等众多智能技术将高校图书馆原本分散的服务进行统一，使大数据时代的高校图书馆服务真正地与用户联系在一起，为其提供更加优质的信息资源与服务。

2.3 方法介绍

由式(4)可以看出，临边观测的滚动角只与卫星地心距r、地球半径Re和观测高度Δh有关。r可通过调用STK软件中的HPOP模型求得；Δh由任务需求决定；由于地球形状不规则，无法确定具体的Re值，因此无法直接利用式(4)求解滚动角φ。本文根据卫星动力学及临边观测几何关系，给出了滚动角数值解求法，具体流程见图3。在地球为理想球形假设的基础上(Re=6 378.137 km)，联立式(2)和式(4)，求得在二体模型下的滚动角解析解φ0，并以φ0作为初值，通过STK软件建模，在HPOP模型下迭代求出满足精度要求的滚动角数值解。其中：t为预设误差；Δhi为高度计算误差；i为迭代次数；迭代公式φi=f(φi-1)由临边观测的几何关系推导得出，具体推导过程如下。

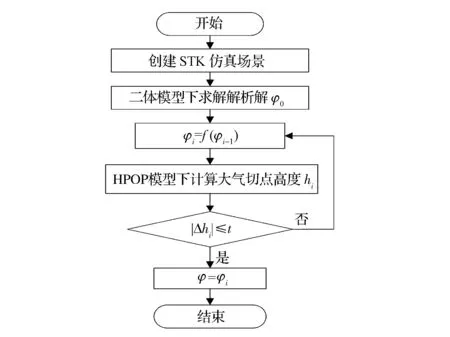
图3 滚动角计算流程Fig.3 Flow for computing roll angle

由图2的几何关系得

(5)

式中：Δh1为滚动角φ1时WSG84地球模型下的观测高度；Δh2为滚动角φ2时WSG84地球模型下的观测高度；Re1和Re2分别为切点P1和P2所在地理位置对应的地球实际半径。

令Re1=Re2，故

(6)

对于大气切点高度，可以通过STK/VectorGeometryTool工具创建切点，再通过STKReport命令直接输出[10]。

2.4 误差分析

地球临边观测卫星的姿态角计算误差主要来自卫星姿态控制精度、遥感器安装精度、地球形状模型和轨道外推模型。其中：卫星姿态控制精度和遥感器安装精度属于卫星自身系统误差，直接影响姿态角计算结果；地球形状模型和轨道外推模型属于外部计算误差，分别影响大气高度值和卫星预报位置，继而影响姿态角的计算结果。若考虑姿态控制精度σ1，遥感器安装精度σ2，地球形状模型导致的大气高度误差σ3，轨道外推模型导致的卫星径向位置预报误差σ4，则推导得到这些误差导致的计算误差Δσ1，Δσ2，Δσ3，Δσ4分别为

(7)

式(7)中，Δσ4是在地球为理想球形的假设下得到的，后续可考虑采用更精确的地球形状模型来分析轨道外推模型精度引起的计算误差。

3 仿真分析

3.1 计算方法比较

假设卫星的轨道为700 km高的太阳同步轨道，对100 km、50 km、20 km高度地球临边大气进行观测，迭代误差设置为5.00×10-3km，观测时间为2016-01-01T00:00:00(UTC)，本文方法及二体模型方法的计算结果如表1所示，其中STK软件验证高度指利用STK软件HPOP模型结合WSG84地球模型求得的大气高度。

由表1不难看出，在理想球形假设的二体模型方法下，计算误差超过了3.00 km；而本文方法的计算误差控制在预定误差5.00×10-3km以内，两种方法的计算误差相差约600倍。同时，利用本文方法，每次的迭代次数均控制在5次以内，收敛迅速。由此可见，本文方法计算精度高，收敛迅速，可有效解决地球临边观测卫星的姿态角计算问题。

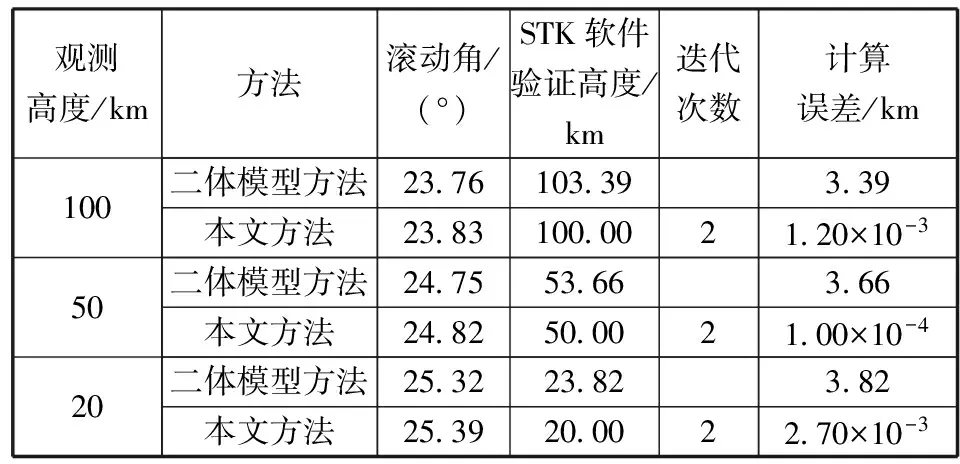
表1 两种方法计算结果比较

3.2 单轨100 km高度大气临边观测

卫星轨道为700 km高的太阳同步轨道，初始姿态对地定向，考虑卫星1个轨道周期内(5 922.26 s)对100 km高度的大气进行临边观测，预设误差为5.00×10-3km。以二体模型方法求得的解析解25.32°作为初值，利用本文方法求得卫星滚动角的变化如图4所示，对应的切点大气实际高度如图5所示，卫星遥感器在1个轨道周期内切过的大气轨迹(地球固连坐标系下)如图6所示。

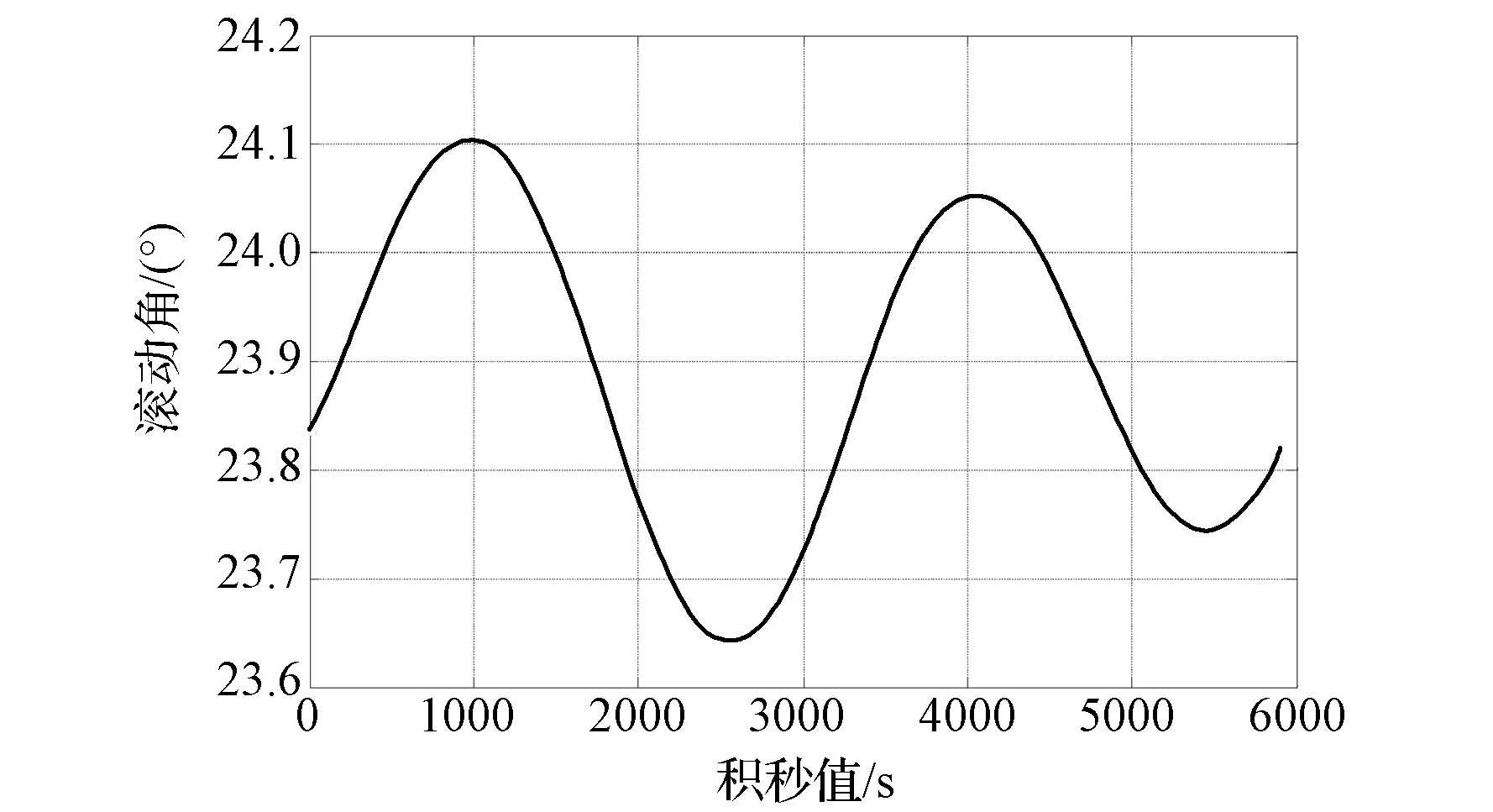
图4 滚动角变化曲线Fig.4 Graph of roll angle change

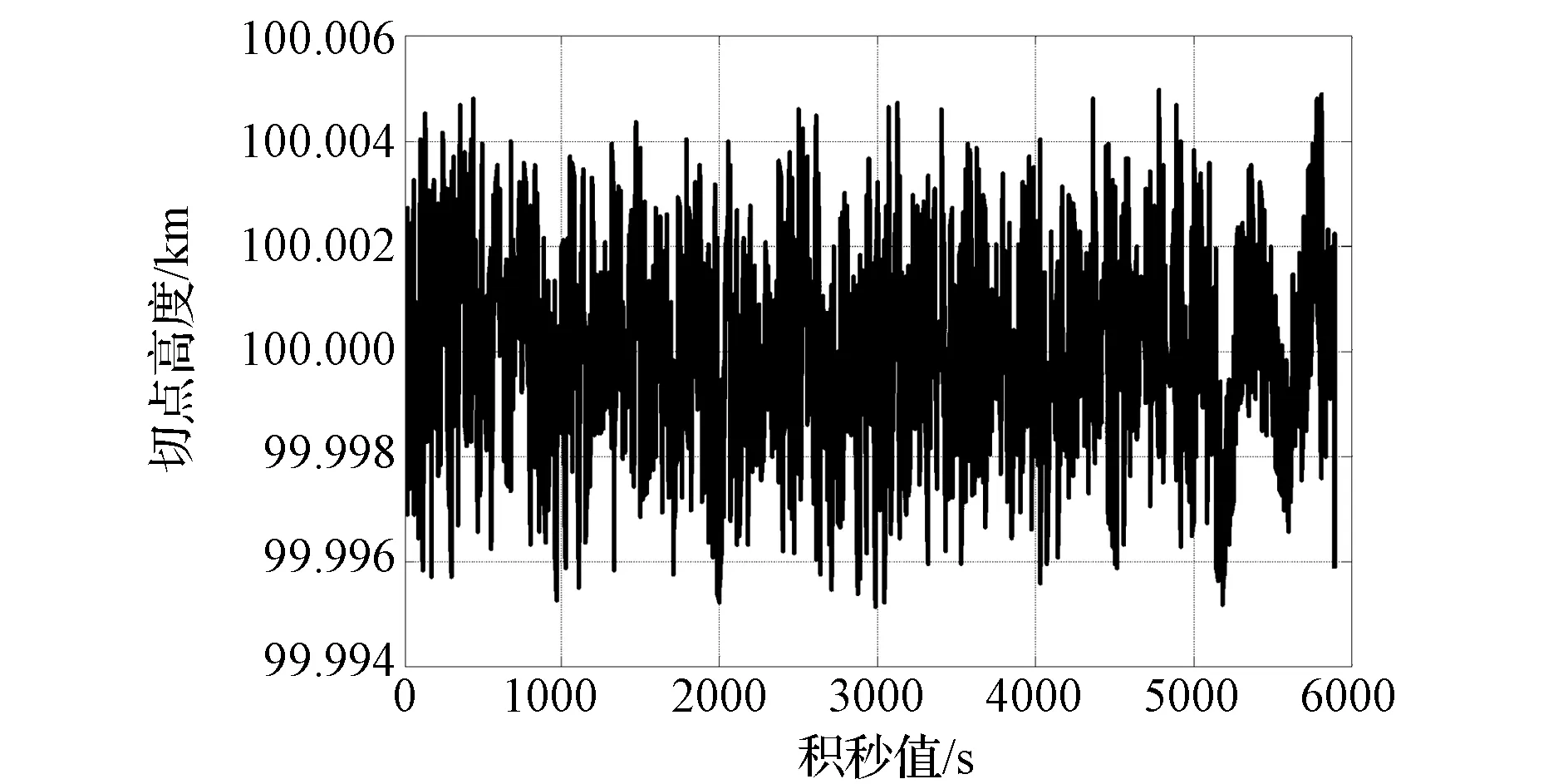
图5 切点大气实际高度变化曲线Fig.5 Corresponding altitude change of tangent atmosphere

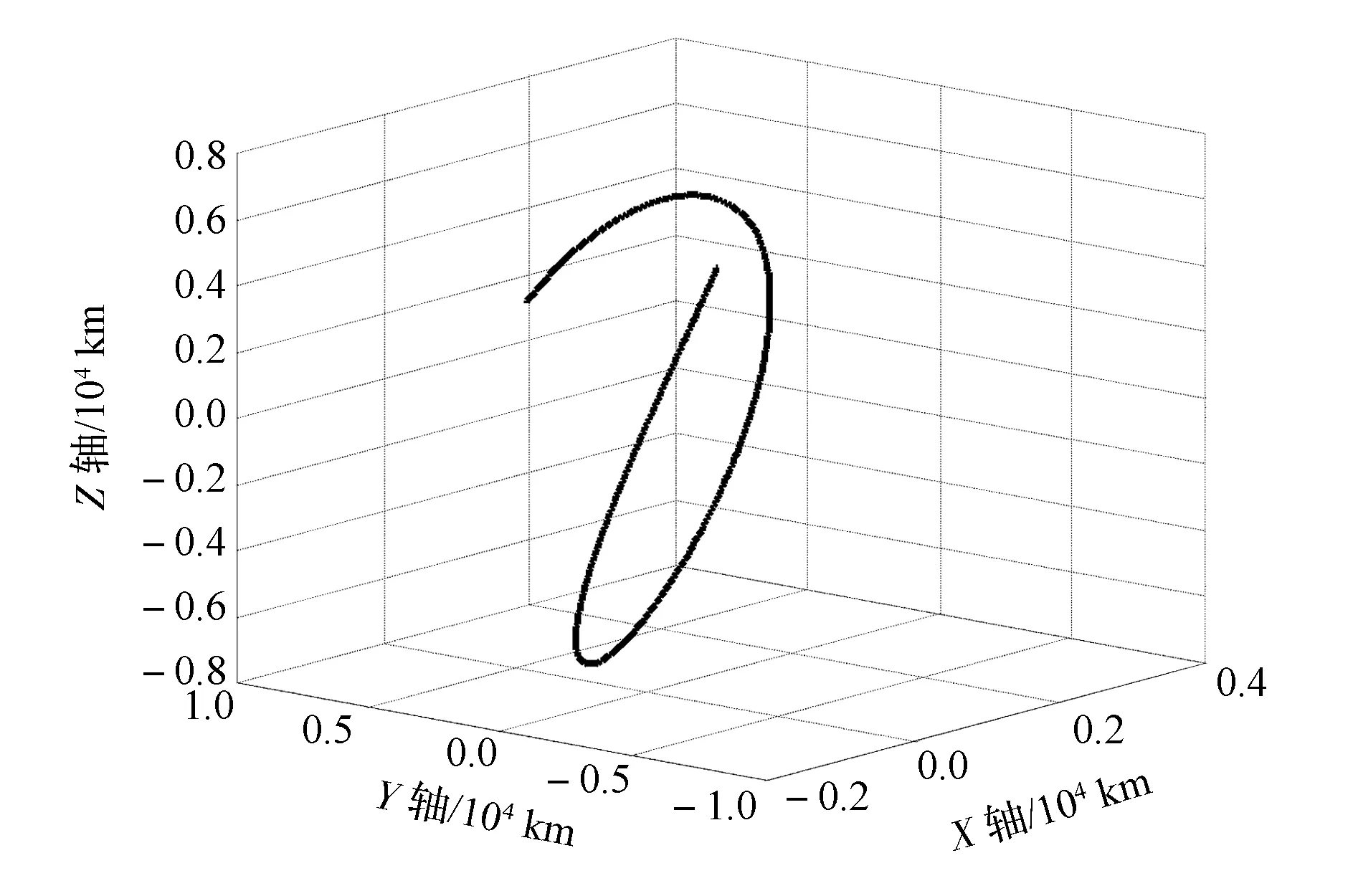
图6 切过的大气轨迹示意Fig.6 Tracing points of tangent atmosphere

由图4可知，卫星滚动角随时间呈正弦曲线变化。在1个轨道周期内，滚动角变化曲线出现2个波峰和2个波谷。其中：波峰出现的时刻分别为第979 s和第4065 s，此时卫星星下点正好处于南北极点处；波谷出现的时刻分别为第2553 s和第5449 s，此时卫星星下点正好处于赤道附近。这主要是因为地球在赤道处的半径最大，在两极的半径较小。因此，观测同样高度的临边，在两极时卫星姿态向地心方向偏得最严重，在赤道时向地心方向偏得最小。

由图5可知，利用本文方法得到的切点大气高度变化范围为99.994～100.005 km。对比二体模型方法的计算误差(如图7所示)，显然本文方法计算精度较高。

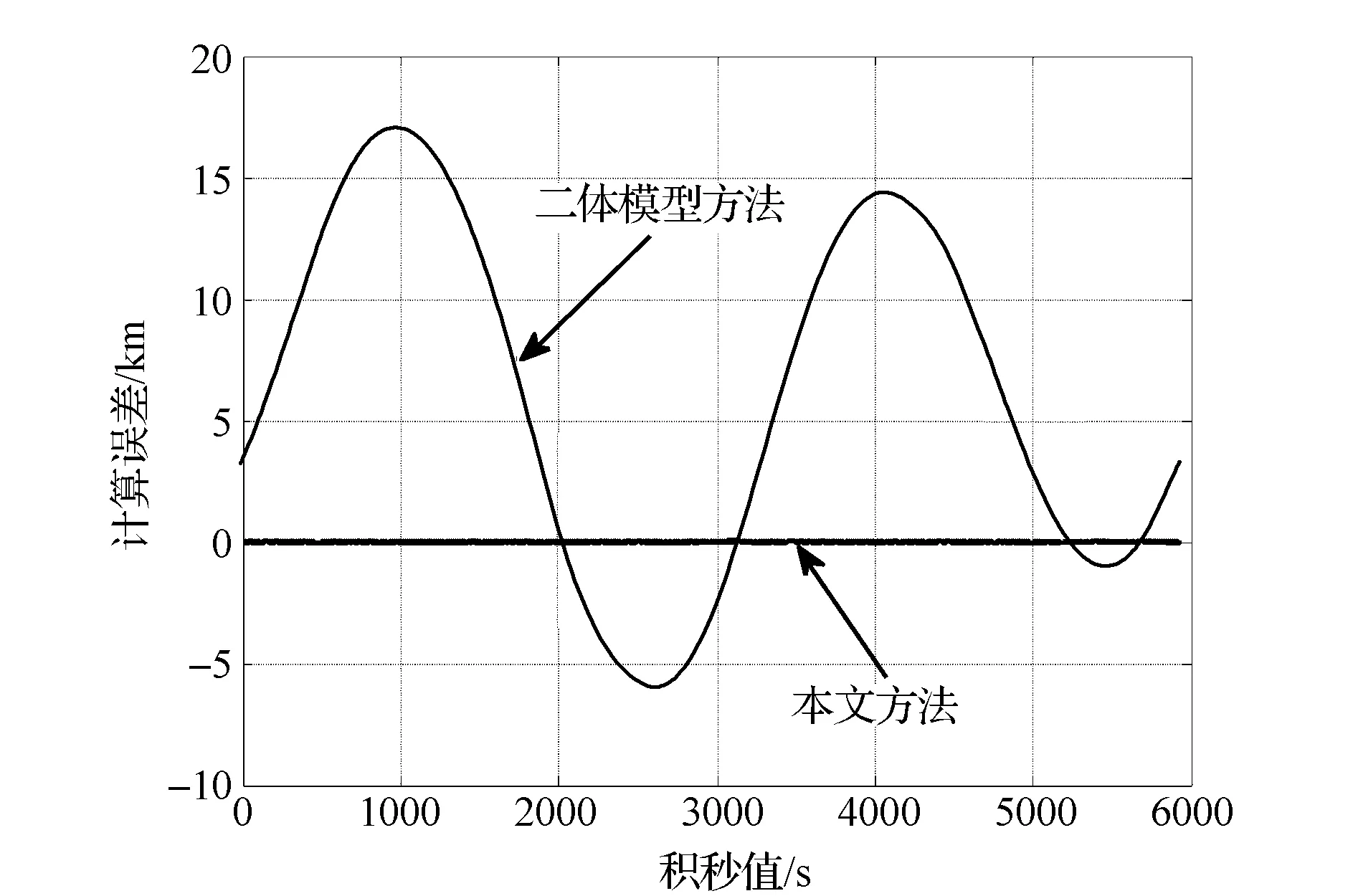
图7 两种方法计算误差对比Fig.7 Calculation error comparison of two methods

3.3 全天候20 km高度大气临边观测

卫星轨道为700 km高的太阳同步轨道，初始姿态对地定向，考虑卫星1 d对20 km高度大气临边观测。利用本文方法得到卫星滚动角变化曲线和切过的大气高度变化曲线，分别如图8和图9所示。为了更直观了解20 km高度大气临边观测情况，图10和图11给出了卫星1 d内切过的20 km高度大气轨迹的三维图(地球固连坐标系下)和二维图。

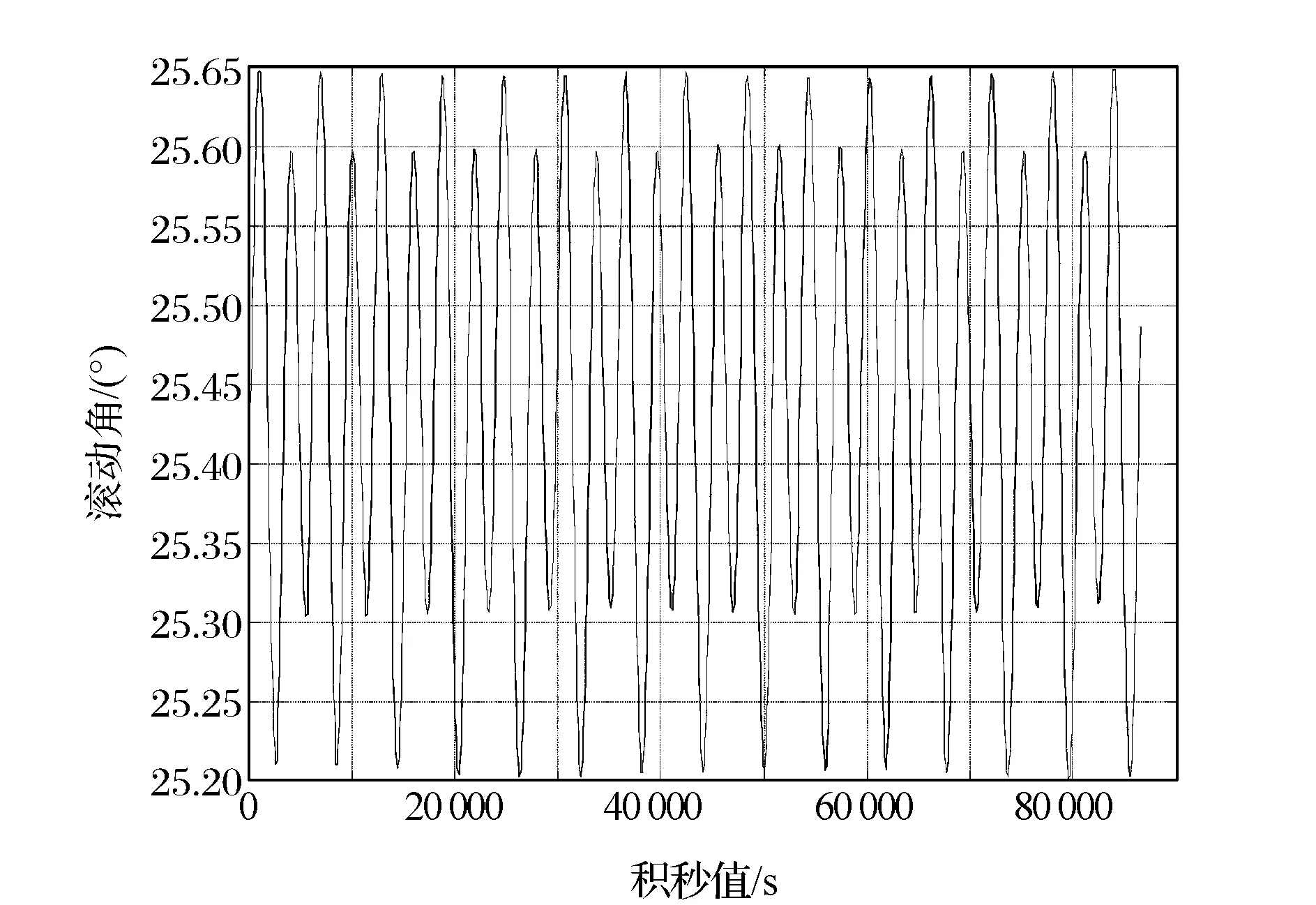
图8 1 d内滚动角变化示意Fig.8 Graph of roll angle change in one day

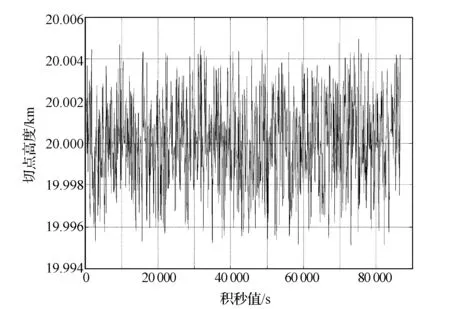
图9 1 d内切过的大气高度变化示意Fig.9 Altitude change of tangent atmosphere in one day

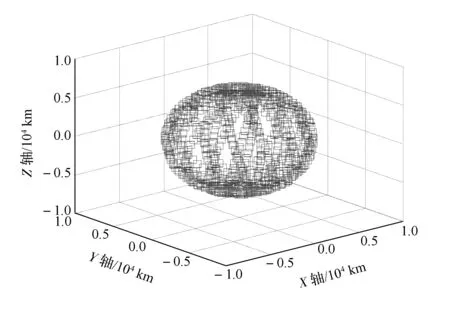
图10 1 d内切过的大气轨迹三维图Fig.10 3-D view of tracing points of tangent atmosphere in one day

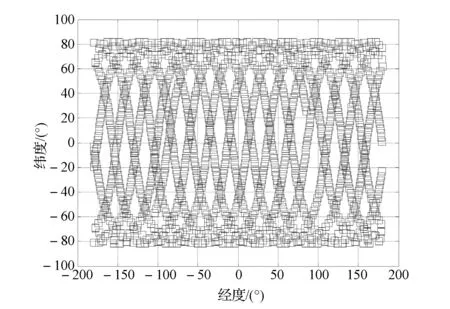
图11 1 d内切过的大气轨迹二维图Fig.11 2-D view of tracing points of tangent atmosphere in one day

从图8可以看出，卫星滚动角呈周期性变化，且变化周期与卫星轨道周期几乎一致。这主要是由地球形状和卫星周期性运动造成的。当卫星星下点纬度接近0°时，观测到的是赤道上空的大气，此时地球半径最大，故卫星在赤道上空进行临边观测时滚动方向上的姿态机动量较小。

地球1 d内绕自转轴转动360°，因此卫星全天候的临边观测可以保证扫过整个经度上的大气。另外，700 km高的太阳同步轨道卫星，单轨覆盖的纬度范围为[81.84°S，81.83°N]。因此，利用本文方法，在1个回归周期内可以覆盖经度[180°E，180°W]、纬度[81.84°S，81.83°N]的临边大气。

3.4 误差分析

假设卫星姿态控制精度为0.005°，遥感器安装精度为0.000 1°，地球形状模型引起的大气高度误差为0.05 km，轨道外推模型导致的卫星径向位置预报误差为0.10 km，则由式(7)计算得到20 km和100 km地球临边观测时的姿态角计算误差，见表2。

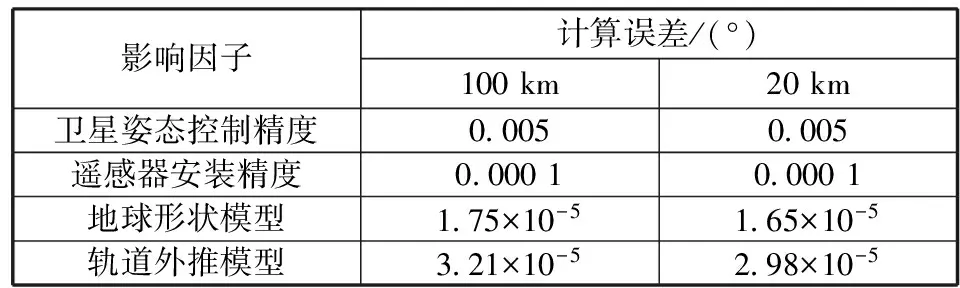
表2 误差分析结果

由表2可以看出：当地球形状模型精度优于0.05 km，轨道预报精度优于0.10 km时，与卫星姿态控制精度和遥感器安装精度相比，它们引起的计算误差很小。因此，采用本文方法引起的计算误差主要来源于卫星自身的姿态控制精度和遥感器安装精度。

4 结束语

本文针对地球临边观测卫星的姿态角计算问题，提出了一种利用STK软件的高精度分析方法，并给出了20 km和100 km临边观测的计算结果。基于仿真分析结果，可以对实际临边观测任务中的卫星姿态导引律进行验证评估，也可以为观测大气的区域规划提供依据；同时，根据测轨数据及姿态实测数据，计算出实际的高度，可以对任务结果进行验证评估。需要注意的是，在本文的仿真算例中，仅考虑了卫星沿一个方向(向地心方向)的姿态机动，在实际任务中，为了提高观测效率，要求卫星姿态在其他方向(偏航)也要进行机动。这将是后续研究的重点，通过引进优化算法使卫星在临边观测任务中实现高精度和高效率的观测。

References)

[1]Fleig A, Rault D F. Ozone vertical profiles in the upper troposphere and stratosphere from the OMPS limb sensor[C]//Proceedings of SPIE Remote Sensing 2011. Bellingham，WA：SPIE，2011

[2]Rault D F, Spurr R. The OMPS limb profile instrument two-dimensional retrieval algorithm [C]//Proceedings of SPIE Remote Sensing 2010. Bellingham，WA：SPIE，2010

[3]Dittman M G, Leitch J W, Chrisp M, et al. Limb broad-band imaging spectrometer for the NPOESS ozone mapping and profile suite (OMPS)[C]//Proceedings of SPIE 4814， Earth Observing System Ⅶ，120. Bellingham，WA：SPIE， 2002: 120-130

[4]刘林.航天器轨道理论[M].北京：国防工业出版社，2000

Liu Lin. Spacecraft orbit theory [M]. Beijing: National Defense Industry Press, 2000 (in Chinese)

[5]杨嘉墀.航天器轨道动力学与控制[M].北京：中国宇航出版社，1995

Yang Jiachi. Spacecraft orbit dynamics and control [M]. Beijing: China Astronautics Press, 1995 (in Chinese)

[6]Kyle T, Alfriend H S, Dong W G. Gravitational perturbations nonlinearity and circular orbit assumption effects on formation flying control strategies [J]. Advances in the Astronautical Sciences, 2000, 104(6):139-158

[7]于凤军. 地球自转、形状和重力加速度随纬度的变化[J]. 大学物理，2013，32(6):14-17

Yu Fengjun. The rotation and shape of earth and the gravity acceleration’s variety with latitude [J]. College Physics，2013，32(6): 14-17 (in Chinese)

[8]Janz S J, Hilsenrath E, Flittner D E, et al. Rayleighscattering attitude sensor[C]//Proceedings of SPIE’s 1996 International Symposium on Optical Science, Engineering and Instrumentation. Bellingham，WA：SPIE， 1996: 146-153

[9]Hilsenrath E, Bhartia P K. Global Environmental Monitoring Satellite (GEMS): a pathfinder to measure gas constituents and aerosols in the earth’s lower atmosphere [C]//Proceedings of SPIE’s 1996 International Symposium on Optical Science, Engineering and Instrumentation. Bellingham，WA：SPIE，1996：224-330

[10]杨颖, 王琦. STK在计算机仿真中的应用[M].北京: 国防工业出版社，2005

Yang Ying, Wang Qi. STK applied in computer simulation [M]. Beijing: National Defense Industry Press, 2005 (in Chinese)

[11]章仁为.卫星轨道姿态动力学与控制[M].北京: 北京航空航天大学出版社，1998

Zhang Renwei. Satellite orbit and attitude dynamics and control [M]. Beijing: Beihang University Press, 1998 (in Chinese)

[12]Curtis F Gerald, Patrick O Wheatley.应用数值分析[M].吕淑娟，译.北京：机械工业出版社，2006

Curtis F G, Patrick O W. Applied numerical analysis [M]. Lv Shujuan, translated. Beijing: China Machine Press, 2006 (in Chinese)

(编辑：夏光)

Simulation Analysis Method on Satellite Attitude Angle in Earth Limb Observation

ZHU Yongsheng HU Haiying ZHENG Zhenzhen SU Ruifeng ZHANG Keke

(Shanghai Microsatellite Engineering Center, Shanghai 201203， China)

A simulation analysis method using STK is presented to calculate the attitude of a satellite for limb observation. The STK simulation scenario is created by connecting STK software. The two-body model is utilized to perform an analytical solution, which provides a reasonable initial guess for subsequent accurate iterative calculation. The WGS84 model is used to improve the initial solution by calling the HPOP (high precision orbit propagator) and the iterative formula. Taking the 20km and 100km limb observation for example, both the proposed method and the two-body method are employed to calculate the attitude angle. And the results show that the method proposed in this paper has faster convergence and higher accuracy.

earth limb observation； satellite attitude angle； high precision calculation

2014-05-19；

2015-06-18

上海市科委扬帆计划(14YF1413600)

朱永生，男，硕士，从事航天器动力学与控制研究工作。Email：juesin@163.com。

V412.4

A

10.3969/j.issn.1673-8748.2015.04.007