2.5D角联锁织物厚向压缩特性的实验研究

万喜莉，孙 颖，陈 利，李嘉禄

(天津工业大学先进纺织复合材料教育部和天津市省部共建重点实验室，天津 300387)

三维机织技术是利用多层经纱织造方法，由多层经纱接结多层纬纱形成具有一定厚度的三维整体织物。其中，经纱采用分层接结的方法，将相邻纬纱层接结可形成角联锁机织物，简称为2.5D织物。在2.5D角联锁机织物基础上，沿织物经向、纬向和厚度方向引入或同时引入纱线，可形成多种衍生组织结构，包括2.5D结构、2.5D衬经结构、2.5D衬纬结构和2.5D衬经衬纬结构。2.5D角联锁织物不仅仿形性好、层间连接强度高，适合于大型构件，而且可最大限度地减小机械加工对其增强复合材料承载能力的损伤。采用树脂传递模塑(tesin transfer molding，RTM)、树脂膜渗透 (resin film infusion，RFI)和热压罐成型等工艺将织物制成复合材料的过程中，干态的织物增强体不可避免地经历着厚度方向压缩后浸渍树脂的复合固化过程。在厚度方向压缩作用下，织物内部单根纤维及纱线之间发生移动，纤维及纱线间孔隙减小，这不但影响树脂在织物中的流动性和浸润性［1］，而且一定程度上决定了复合材料的细观结构和力学性能。相关研究工作表明，织物经压缩作用产生的几何结构变化，会导致其复合材料在拉伸过程中发生应变硬化现象［2］;织物压缩作用后纱线扭结屈曲［3］，是构成了复合材料承载失效的主要诱因［4－5］，因此，用于复合材料增强体，2.5D 角联锁机织物厚向压缩性能是织物重要性能之一。

机织物厚度方向压缩性能的研究方法主要有实验分析和模型预测2种。Bannister等［6］研究了在4.14 MPa和6.9 MPa 2种压缩载荷作用下三维角联锁机织物的纱线结构，结果表明，高度压缩织物可达到较高的纤维体积含量，但经纱分布均匀性下降的同时纬纱的屈曲程度增加。Chen等［7］建立了多层平纹织物压缩行为非线性模型，分析了织物厚度－压缩应力关系，经验证该模型适用于玻璃纤维和碳纤维的多层平纹织物。Grujicic等［8］基于平纹织物厚度－压缩应力关系，采用梁单元模拟四分之一单胞内经纬纱，建立了压缩应力与织物有效渗透率之间的关系，结果发现，织物有效渗透率随压缩应力的增加先急剧下降而后下降趋势趋缓。Potluri等［9］利用最小能量原理和织物风格评价系统(Kawabata evaluation system，KES)，建立了织物三维压缩模型，模型考虑了纤维及纱线在压缩应力作用下的结构变化，设计实验对比分析了只考虑纱线弯曲、只考虑纱线压缩以及既考虑纱线弯曲又考虑纱线压缩等3种情况下织物三维压缩模型的预测结果，结果表明，既考虑纱线弯曲又考虑纱线压缩的模型准确性较高。Kruckenberg等［10］研究了多层平纹织物的准静态及动态压缩行为发现，700 kPa压缩应力作用下，织物经向截面内经纱波长增大，波幅减小，纬纱宽度增大。Mahadik等［11－12］研究了 2.5D 和2.5D 衬经织物厚度方向压缩对织物纤维体积含量、细观结构的影响，并测试了不同纤维体积含量2.5D衬经织物增强复合材料的压缩性能，结果发现，织物压缩后纤维体积含量增加，经向压缩性能呈现先降低后升高的现象，而纬向压缩性能无明显变化。

本文以2.5D角联锁织物中常用的2.5D衬经结构织物为例，从宏观和细观角度研究了碳纤维2.5D衬经织物厚度方向的压缩性能。采用实验方法获得织物厚度－压缩应力关系，分析宏观压缩特性的同时，与用于多层平纹织物压缩模型的预测结果进行对比。在4种压缩应力作用下利用RTM复合工艺制备2.5D衬经结构复合材料板，通过光学显微镜观测并分析复合材料板的细观结构特征，定量分析经纱、衬经纱和纬纱的屈曲变化情况，为复合材料用2.5D角联锁机织物的结构设计，特别是织物厚度设计提供参考。

1 实验测试

图1示出2.5D衬经结构。

图1 2.5D衬经结构Fig.1 2.5D with stuffer warp

1.1 试样制备

2.5D衬经织物中经纱为东丽T300-3K碳纤维，衬经纱和纬纱为东丽T700-12K碳纤维，如图2所示。织物尺寸为100 mm×135 mm×5.5 mm，纤维体积含量为46.3%，织物面密度为0.48 g/cm2，织物参数见表1。

图2 2.5D衬经织物Fig.2 2.5D with stuffer warp woven fabric

1.2 压缩实验

参考GB 24442.2—2009《纺织品压缩性能的测定第1部分:恒定法》，在岛津万能材料试验机(AG-250KNE)上测试织物厚度方向压缩性能，如图3所示。根据织物截面形状尺寸，压缩速度设置为0.5 mm/min，压脚面积设置为400 cm2。压缩应力由载荷与织物受力面积的比值得到。

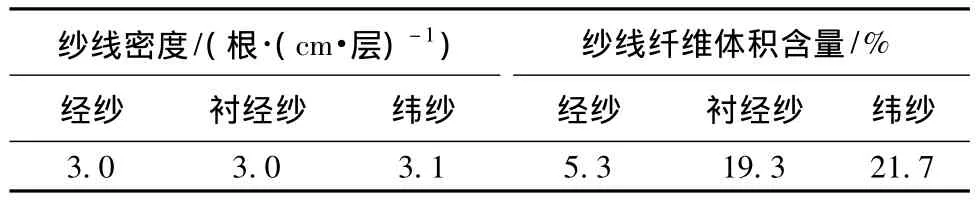
表1 织物参数表Tab.1 Parameters of fabric

图3 织物厚度方向压缩性能测试Fig.3 Compression test in thickness direction of fabric

1.3 织物厚度与压缩应力的关系

2.5D衬经织物厚度-压缩应力曲线测试结果如图4所示。由图可看出，织物厚度方向压缩过程分为3个阶段:低应力线性阶段、非线性阶段和高应力线性阶段。低应力线性阶段主要发生纱线滑移，经纬纱产生嵌套现象，纱线间隙减小，越来越多内部纤维承受载荷;低应力非线性阶段主要发生纤维滑移，纤维间孔隙减小，经纬纱变形，织物厚度的减小变得困难;当纤维滑移接近极限，随压缩应力的增加，纤维本身发生变形，这就是高应力线性阶段，纤维可压缩性影响织物厚度，而纤维可压缩性与纤维种类、纤维泊松比及弹性模量等有关。当纤维变形达到极限后，随压缩应力增加织物厚度不再减小，织物的最小厚度为3.32 mm。

Chen等［7］忽略织物的面内变形，提出多层平纹织物厚度和压缩应力之间的关系，如式(1)所示。式中:P为压缩应力;Cb(T)为织物的可压缩性;T为织物厚度;T0为织物初始厚度。

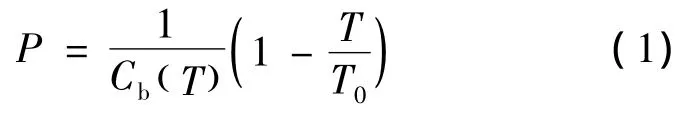
其中，多层平纹织物可压缩性Cb(T)是以织物厚度T为自变量的函数值，可由式(2)计算。

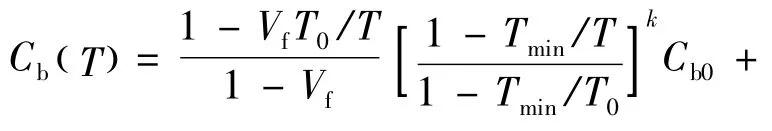
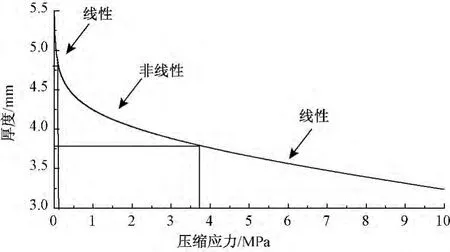
图4 2.5D角联锁机织物厚度－压缩应力曲线Fig.4 Thickness-pressure curve of 2.5D angle-interlock woven fabric

式中:Vf为初始纤维体积含量;Tmin为织物最小厚度;Cb0为初始织物的可压缩性;Cf为纤维可压缩性;k为与纤维种类、纤维细度和织物结构有关的经验指数。Chen发现取经验值k=2适用于玻璃纤维和碳纤维多层平纹织物。

由2.5D衬经织物厚度-压缩应力的测试曲线可知，织物的初始可压缩性Cb0为常数，如式(3)所示，Cb0为2.40 MPa－1。纤维的可压缩性Cf与纤维的弹性模量E和泊松比v有关，可由式(4)求出，碳纤维的泊松比为0.2，弹性模量为230 GPa，可得出碳纤维的可压缩性为 7.83 ×10－6MPa－1。

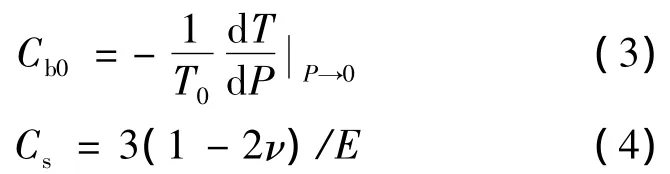
本文基于Chen的研究工作，取经验指数k分别为2、3和4，得到模型预测结果，如图5所示。

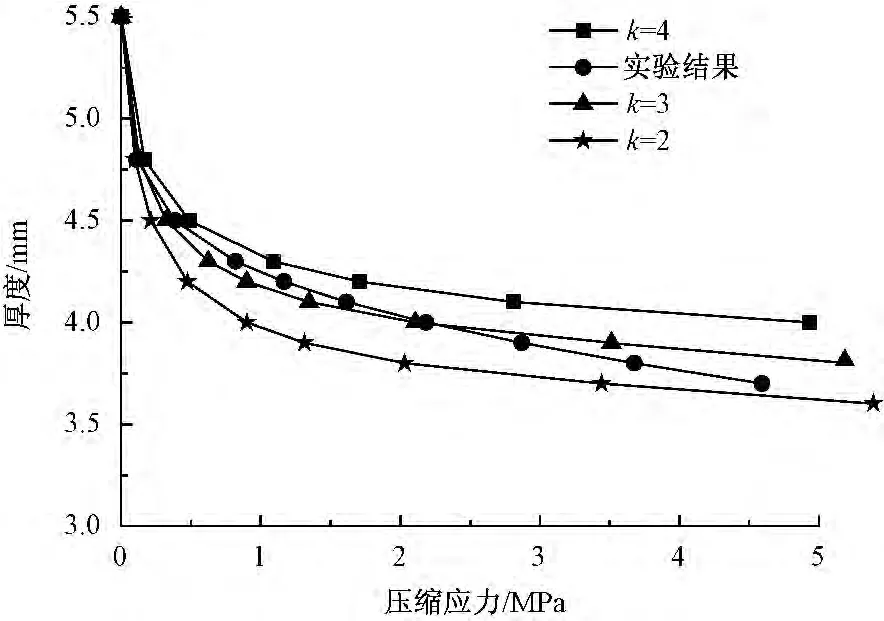
图5 实验结果与模型预测结果的比较Fig.5 Comparison between experimental results and modelling predictions

由图发现，当取k=3时预测结果与实验结果较为接近，因此，当压缩应力小于3 MPa时，碳纤维2.5D衬经织物可采用k=3的多层平纹织物压缩模型预测织物厚度与压缩应力的关系。对于不同纤维、不同结构、不同结构参数2.5D角联锁机织物厚度与压缩应力之间关系还有待进一步验证。2.5D角联锁结构是基于普通平纹织物结构织造而成，选择多层平纹织物压缩模型来预测2.5D角联锁织物的压缩特性有一定的合理性。然而模型的适用范围较小，需在大量实验的基础上进一步优化，建立更为合理的模型来预测不同结构、不同参数的2.5D角联锁结构的压缩特性。

2 纱线结构观测

2.1 纱线截面观测

为研究压缩过程中织物结构变化，在0.05、0.61、2.88、5.30 MPa 4种压缩应力下，将上述2.5D衬经织物复合固化，制得不同厚度的复合材料板，裁切成含有至少2个组织结构的试样，试样尺寸为25 mm×25 mm×T mm，磨抛处理后在光学显微镜下观测织物经向截面和纬向截面内纱线的屈曲状态，经纱所在经向截面、衬经纱所在经向截面和纬纱所在纬向截面如图6～8所示。图中x为经向，y为纬向，z为厚度方向。

2.2 纱线结构观测结果

图6 经纱所在经向截面图Fig.6 Cross-sections in warp direction of warp

图7 衬经纱所在经向截面图Fig.7 Cross-sections in warp direction of stuffer warp

在厚度方向压缩应力作用下，2.5D衬经织物纱线结构变化主要表现为纱线屈曲程度和横截面的变化。借鉴文献［12］中对角联锁织物纱线形态观测和表征方法在经向截面图中截取2个组织循环，以图6(a)中A区的1根经纱为例，沿经纱的中心线取等间距离散点(如图9所示)。将纱线的屈曲形态转化为多个线段。计算每两点之间经纱线段的局部屈曲角，纱线段局部屈曲角定义为纱线段偏离水平基准面的角度，纱线段局部屈曲角计算方法如图10［5］所示。依照此法分别计算4种压缩应力作用下复合材料板中经纱、衬经纱及纬纱的各纱线段的局部屈曲角度，以5°为间隔区间，计算出每个范围的局部屈曲角所占比例，测量结果如图11所示。利用加权平均得出经纱、衬经纱和纬纱的平均屈曲角如图12所示。

图8 纬纱所在纬向截面图Fig.8 Cross-sections in weft direction of fabric

图9 经纱中心线的离散化Fig.9 Discretization of yarn centerline

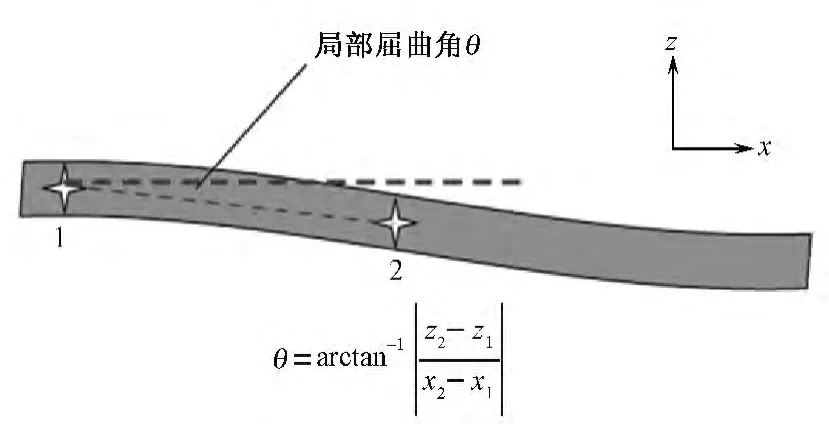
图10 纱线段局部屈曲角的计算方法Fig.10 Method for calculating local angle of yarn section

2.5D衬经织物中衬经纱和纬纱基本呈伸直状态，经纱因接结相邻纬纱层提供厚度方向的连接与增强而具有较高的屈曲水平。经纱与纬纱的交织点处存在较大孔隙，压缩过程中单根纤维间和纱线间发生滑移，织物孔隙随压缩应力的增加明显减小。结合图6和图11(a)可看出，在0.05 MPa的压缩应力作用下，经纱和纬纱发生滑移，局部屈曲角为0～10°的经线段比例较小，局部屈曲角≥10°的经纱段比例较大，经纱屈曲程度较高;当压缩应力增至0.61 MPa时，经纬纱交织点处的纤维发生滑移，纤维及纱线间孔隙减小，局部屈曲角为0～10°经纱段比例增加，经纱屈曲程度降低，表层的经纱明显变为扁平;压缩应力增至2.88 MPa时，局部屈曲角为0～5°纱线段所占比例最高，局部屈曲角为10°～30°经纱段比例下降，所有经纱变为扁平;随着压缩应力继续增加，交织点处的纤维继续向远离交织点处滑移，纱线扁平程度下降，局部屈曲角为0～5°经纱段比例下降，其他局部屈曲角的经纱段比例上升，说明压缩应力过大导致经纱的屈曲程度增加。

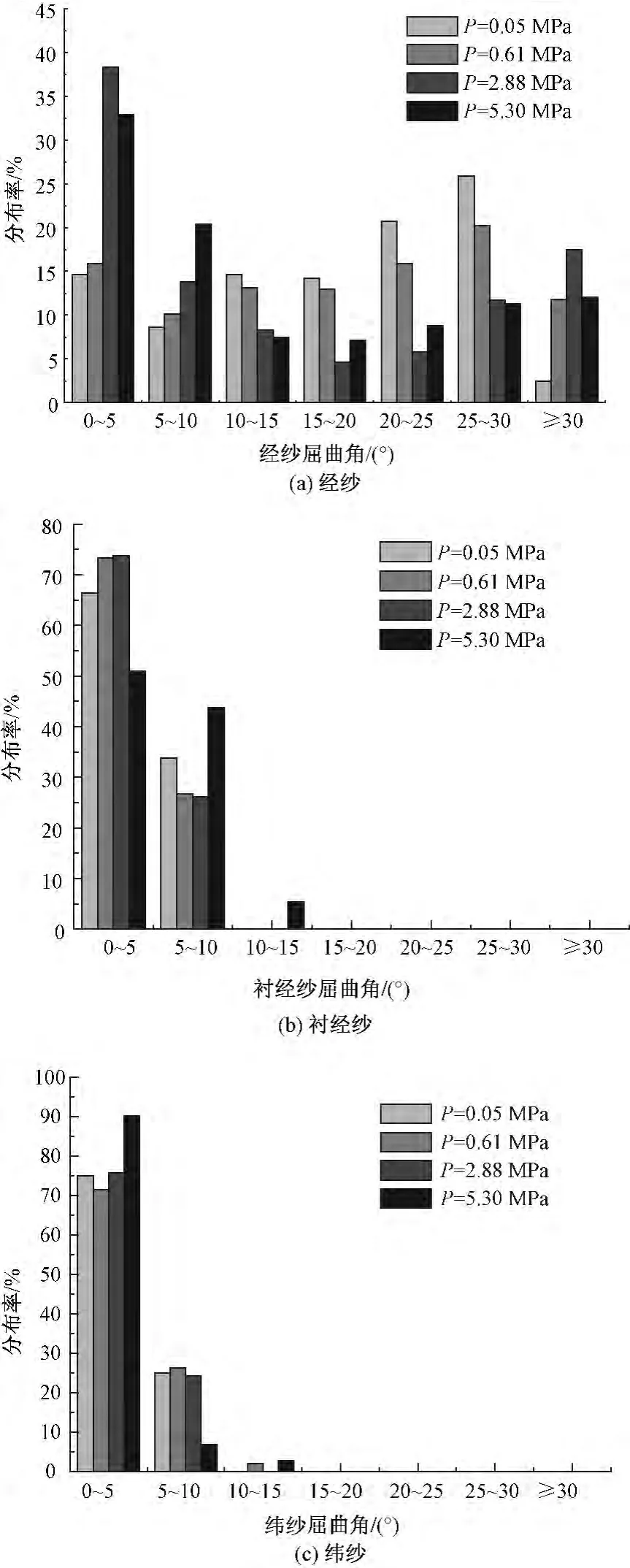
图11 经纱、衬经纱和纬纱纱线段局部屈曲角分布Fig.11 Frequency distribution of warp(a)，stuffer warp(b)and weft yarn(c)segment crimp

压缩应力作用下经纱与纬纱交织点处纤维向远离交织点处滑移，纬纱宽度明显增加，相邻纬纱内纤维滑移方向不同，致使与纬纱嵌套的衬经纱呈相邻纱层对称屈曲状态，如图7所示。2.5D衬经织物中经纱与衬经纱、纬纱的线密度比很小，经纱屈曲程度的变化对纬纱屈曲的影响较小。由图7、8可看出，衬经纱和纬纱的屈曲程度无明显变化，图11(b)、(c)表明衬经纱和纬纱无局部高屈曲纱线段，纱线段局部屈曲角基本趋于15°以下。

图12表明经纱的平均屈曲角最高，当压缩应力增至2.88 MPa时，经纱平均屈曲角由初始的18°降至14°。这是由于压缩应力作用下织物厚度减小阻碍了经纱在纬纱层间的滑移量。继续增大压缩应力时，衬经纱的屈曲程度增加，而此时纬纱的平均屈曲角降低，趋于伸直。

综上，对于碳纤维2.5D衬经织物，当厚度方向压缩应力为0.61～2.88 MPa时，复合材料中经纱屈曲程度明显降低，衬经纱和纬纱的屈曲程度无明显变化，有利于实现纤维性能-织物-复合材料性能的转化。

3 结语

1)通过对碳纤维2.5D衬经织物厚度方向压缩性测试，获得织物厚度与压缩应力的关系，与基于多层平纹织物压缩模型预测结果进行对比。研究发现，当压缩应力小于3 MPa时，经验指数取为3的多层平纹织物压缩模型可用于2.5D衬经织物厚度与压缩应力关系估算。对于不同纤维、不同结构、不同结构参数2.5D角联锁织物厚度与压缩应力之间关系还有待进一步验证。

2)2.5D衬经结构织物中经纱的屈曲程度最高，厚度方向压缩应力的增加使得经纱屈曲程度降低，而当压缩应力超过一定范围时，经纱屈曲程度反而增加;因为衬经纱和纬纱无局部高屈曲纱线段，纱线基本呈伸直状态，在压缩过程中纱线的屈曲程度变化不明显，当压缩应力超过一定范围时，衬经纱的屈曲程度增加，这不利于纤维性能—织物—复合材料性能的转化，纬纱伸直度增加，有利于提高织物纬向力学性能。

［1］ CHEN B X，LANG E J，CHOU J W.Experimental and theoretical studies of fabric compaction behavior in resin transfer molding［J］.Materials Science and Engineering A，2001，317(1/2):188－196.

［2］ COX B N，DADKHAH M S，MORRIS W L.On the tensile failure of 3D woven composites［J］.Compos A Appl Sci Manuf，1996，27(6):447 －458.

［3］ COX B N，DADKHAH M S，INMAN R V，et al.Mechanisms of compaction failure 3D composites［J］.Acta Metall Mater，1992，40(12):3285 －3298.

［4］ CALLUS P J，MOURITZ A P，BANNISTER M K，et al.Tensile properties and failure mechanisms of 3D woven GRP composites［J］.Compos A Appl Sci Manuf，1999，30(11):1277－1287.

［5］ MAHADIK Y，ROBSON B K A，HALLETT S R.Characterisation of 3D woven composite internal architecture and effect of compaction［J］.Composites:Part A，2010，41(7):872 －880.

［6］ BANNISTER M，HERSZBERG I，NICOLAIDIS F，et al.The manufacture of glass/epoxy composites with multilayer woven architectures［J］.Composites:Part A，1998，29(3):293－300.

［7］ CHEN B，CHENG A H D，CHOU T W.A nonlinear compaction model for fibrous preforms［J］.Composites:Part A，2001，32(5):701 －707.

［8］ GRUJICIC M，CHITTAJALLU K M，WALSH S.Effect of shear，compaction and nesting on permeability of the orthogonal plain-weave fabric preforms［J］.Materials Chemistry and Physics，2004，86(2/3):358 －369.

［9］ POTLURI P，SAGAR T V.Compaction modelling of textile preforms for composite structures［J］.Composite Structures，2008，86(1/3):177 －185.

［10］ KRUCKENBERG T，YE L，PATON R.Static and vibration compaction and microstructure analysis on plain-woven textile fabrics［J］.Composites:Part A，2008，39(3):488－502.

［11］ MAHADIK Y， HALLETT SR. Effectoffabric compaction and yarn waviness on 3D woven composite compaction properties［J］.Composites:Part A，2011，42(11):1592－1600.

［12］ MAHADIK Y，HALLETT S R.Finite element modelling of tow geometry in 3D woven fabrics［J］.Composites:Part A，2010，41(9):1192 －1200.