基于BLT 方程的外场照射下线缆终端耦合响应分析

周 香 曹玉梅 臧家左

(1 东南大学电磁兼容试验室，南京211189)

(2 苏州博世汽车部件有限公司，苏州215021)

(3 电磁环境效应航空科技重点试验室，沈阳110035)

随着飞机内电子设备的发展，信号传输的种类也越来越多，而电缆是信号传输的载体，在高场强的核电磁脉冲环境下，电缆会受到场强的干扰产生感应的电流和电压，导致电缆中传输的信号受到干扰，引起敏感设备的阻塞、烧毁或者不工作［1］.例如，对某飞机平台加装新的短波电台后，出现了电磁干扰问题.具体表现为:在短波电台发射时，无线电高度表输出的高度数值发生变化，忽大忽小，严重时高度数值直接变为零.短波电台对高度表的主要干扰途径是电缆［2］，因此外场照射下线缆终端耦合特性研究对外场照射下系统的线缆敷设具有重要意义.

场线耦合模型主要基于Maxwell 方程推导而来，常用的有3 种:Taylor 模型、Agrawal 模型、Rachidi 模型.这些模型主要是用于描述双导体传输线的场线耦合.随后，在1970年代Baum 等推导了著名的BLT 方程，该方程为场线耦合终端响应提供了一个精简的表达式［3］.BLT 方程是基于传输线理论的，与数值方法计算线缆终端耦合相比，具有物理意义明确、计算量相对较少的优点.国内也进行了基于BLT 矩阵方程的场线耦合研究，李许东等利用BLT 方程求解了线缆终端响应［4-6］.关于场线耦合试验方法的研究，国外学者运用混波室对双绞线和平行双线进行了抗干扰对比分析［7］.

本文基于BLT 方程进行多导体传输线的场线耦合建模，求解线缆终端耦合响应，并利用试验室自主研制的GTEM 小室进行试验，验证了BLT 方程求解场线耦合线缆终端响应的有效性.在此基础上，分析了线缆的长度和间距以及平面波的入射角度和极化角度对场线耦合线缆终端响应特性的影响，以便为线缆敷设提供指导.

1 基于BLT 矩阵方程的入射场激励线缆耦合模型

图1为受外加场激励的三导体传输线.其中，Einc为入射电场;H 为磁场;k 为电磁波方向，指向原点;θp为入射方向与x 轴的夹角;φp为入射方向对yoz 面的投影与y 轴的夹角;h1和h2分别表示信号线距参考地线的距离;L 为线缆并走的长度;Zs，ZL，Z1，Z2为线缆终端的连接负载.图2给出了外加场的极化角度θE，用球坐标系的aθ和aφ表示［6］.

图1 受外加场激励的三导体传输线

图2 外加场的极化角度［3］

对于外加场激励下多导体传输线线缆终端响应，可利用BLT 矩阵方程求解［3］.BLT 矩阵方程可表示为

1.1 终端反射系数

终端反射系数ρ 的表达式为［8］

式中，ρ1为z=0 端的反射系数，ρ1为z=L 端的反射系数，ρ2=

1.2 传输矩阵

传输矩阵Γ 的表达式为

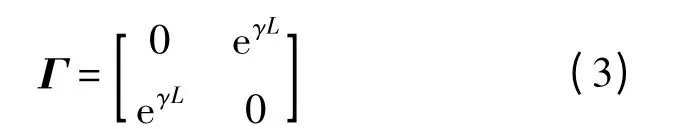
式中，γ 为传播常数.γ=α+jβ，α 为衰减常数，β 为相移常数;当传输线无耗时，α=0，γ=jβ.

1.3 激励源矢量

激励源矢量S 由下式表示［3］:

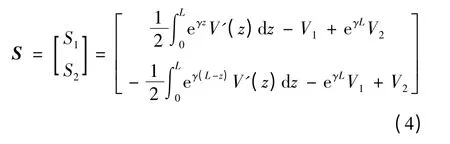
式中，V'(z)为分布电压源;V1和V2为终端集总电压源.

选择平面波作为激励源时，设传输线无耗，激励源矢量中对应的V'(z)，V1，V2值分别为［9］

式中，xk，yk分别为等效源的x 轴和y 轴坐标;φk=分别为沿x 轴、y 轴和z 轴方向的相移常数，βx= －βcosθp，βy= －βsinθpcosφp，为角频率，μ 为介质的磁导率，ε 为介质的介电常数;ex，ey，ez分别为入射电场沿x 轴、y 轴和z 轴方向的分量，ex=sinθEsinθp，ey= －sinθEcosθpcosφp－cosθEsinφp，ez= －sinθEcosθpsinφp+cosθEcosφp.

2 线缆耦合试验

2.1 测试原理

图3为GTEM 小室内场线耦合测试的原理图.由信号源和功率放大器为GTEM 小室提供激励源，该激励源在GTEM 小室产生均匀场E，传播方向k 为由小室的输入端指向小室的终端，对线缆进行照射.将线缆的一个终端连接到频谱仪上，利用频谱仪测试线缆终端耦合到的电压值V.将V 对场强进行归一化得到单位场强的耦合系数.

图3 GTEM 小室内场线耦合测试原理图

2.2 试验布置

图4为线缆在GTEM 小室内的布置图，电磁场的传播方向平行于线缆组成的平面.EUT 为三导体传输线模型，线缆共走的长度为L=0.4 m，导体半径r=0.7 mm，绝缘层厚度t=1.2 mm，线缆的3 个终端连接50 Ω 的负载模拟设备，1 个终端连接频谱仪(频谱仪的阻抗为50 Ω)，用来测试耦合到的信号.场探头用于监测受试线缆位置的场强.

图4 线缆测试布置图

2.3 结果分析

本试验通过LabVIEW 测试程序来控制仪器进行扫频测试.图5为线缆终端耦合试验结果和计算结果的对比曲线图.

由图5可见，试验结果和计算结果的变化趋势比较接近，但由于受试线缆的引入，扰乱了GTEM小室内的场环境，导致GTEM 小室内的电场除主方向(小室高度方向)外，小室宽度方向和电磁场传输方向的场增加，且这种变化与频率相关，导致照射线缆的场与理论场有差异，线缆终端耦合的试验值与计算值存在差异，试验值波动较大.因此，可利用BLT 矩阵方程预测场线耦合的线缆终端响应.

图5 线缆终端耦合试验结果和计算结果

3 影响因素分析

基于上述理论模型，分析线缆长度、线缆间距、线缆终端负载和平面波的入射角度以及极化角度对线缆终端响应的影响.

3.1 线缆长度

保持信号线与参考地线的距离为1 cm，改变线缆长度，计算线缆终端的耦合电压.计算频率分别为10 kHz 和1 GHz.

图6(a)和(b)分别是频率为10 kHz 和1 GHz时线缆终端耦合响应随长度的变化曲线图.10 kHz时，随着长度的增加，线缆终端的耦合电压线性增加;而当频率为1 GHz 时，线缆终端耦合电压大小随着线缆长度改变出现了谐振，但最大耦合电压不再增加.线缆长度为1 ～4 m 时，相对于频率1 kHz，线缆均处于电短状态，而相对于频率1 GHz，线缆均处于电长状态.由此可得:当线缆处于电短状态时，线缆终端耦合电压随着线缆长度的增加而线性增加;当线缆处于电长状态时，线缆终端耦合电压不再随着线缆长度的增加而线性增加，而是振荡变化.因此，当线缆处于电长状态时，在外场照射下，线缆长度对线缆终端耦合较小;连接处屏蔽线缆屏蔽层剥离长度对线缆终端耦合较大，因此需特别考虑屏蔽层剥离长度对场线耦合引起的线缆终端电压的影响.

图6 不同频率下终端耦合电压随线缆长度的变化

3.2 线缆间距

保持线缆长度为1 m，改变信号线距参考地线的距离，计算线缆终端耦合值，计算频率为1 GHz.图7为随着线缆间距变化线缆终端耦合电压值.由图可得，随着线缆间距的增加，线缆终端耦合的电压值呈线性增加.这是由于当线间距变大时，传输线的环路面积增大，就会有更多的电磁场能量耦合到传输线中.因此，布线时应尽量减小线缆间的间距.

图7 线缆间距变化时线缆终端耦合电压值

3.3 平面波的极化角度和入射角度

保持线缆的间距为1 cm，线缆长度为1 m，平面波入射角φp= －90°，极化角度θE=90°，改变平面波的入射角度θp，计算线缆终端的耦合电压，计算频率为1 GHz.图8(a)是线缆终端耦合电压随入射角θp变化的情况.

图8 入射角度和极化角度改变时线缆终端响应

保持线缆的间距为1 cm，线缆长度为1 m，平面波的入射角度φp= －90°，θp=90°，改变平面波的极化角度θE，计算线缆终端的耦合电压，计算频率为1 GHz.图8(b)是线缆终端耦合电压随极化角度θE变化的情况.

结合式(4)、(5)和图8可知，入射角和极化角变化会引起激励源矢量变化，进而影响线缆终端耦合电压.因此，若干扰源在系统内部时，可根据情况通过适当改变源的位置或改变线槽走向减小终端耦合电压.

3.4 线缆终端负载

保持线缆长度为1 m，间距为1 cm，极化角度θE=90°，入射角度θp=90°，φp= －90°，改变线缆终端的负载，计算线缆终端耦合值.图9为不同频率下，线缆终端耦合终端负载的变化情况.由图可见:频率越高，终端耦合电压越大;不同频率下，终端负载对终端耦合电压的影响不同.由于耦合机制不同，高频时，随负载增加，耦合增大，到一定程度后增速趋缓，并在达到最大值后有下降趋势;低频时，负载大小对终端耦合的影响较小，此时，更适合用低频电路的方法分析.

图9 终端负载改变时线缆终端耦合电压

4 结语

本文主要针对三导体传输线建立平面波激励的BLT 矩阵模型，并利用GTEM 小室内场线耦合试验，验证BLT 矩阵方程求解场线耦合模型终端响应的有效性.最后分析了影响线缆终端响应的因素，结果表明:线缆在电短状态时，随着长度增加终端耦合电压增大，在电长状态时，长度变化将不再使线缆终端耦合电压呈线性增加;线缆间距与线缆终端耦合电压呈线性增加的关系;线缆终端耦合电压随入射角度和极化角度的增加呈单调减小或增加;不同频率下，负载对终端耦合电压的影响不同.同时，根据影响因素分析给出了线缆敷设建议.

References)

［1］ 陈晋吉.飞机电磁兼容预测仿真研究［D］.西安:西安电子科技大学电子工程学院，2013.

［2］ 李淑华，宫波，高伟.某机载短波电台干扰无线电高度表的行为级仿真及分析［J］.现代电子技术，2010，33(9):14-17.Li Shuhua，Gong Bo，Gao Wei.Behavioral simulation and analysis of interfering wireless altimeter by airborne shortwave station［J］.Modern Electronic Technique，2010，33(9):14-17.(in Chinese)

［3］ Paul C R.Analysis of multi-conductor transmission lines［M］.New York:John Wiley ＆Sons，2007:598-599.

［4］ 李许东，王庆国，周星，等.基于BLT 方程的传输线网络电磁脉冲响应分析［J］.河北科技大学学报，2011，32(S1):183-186.Li Xudong，Wang Qingguo，Zhou Xing，et al.Analysis of EMP response of transmission lines network based on BLT equation［J］.Journal of Hebei University of Science and Technology，2011，32(S1):183-186.(in Chinese)

［5］ 安霆，刘尚合.基于BLT 方程的电磁干扰建模［J］.高电压技术，2007，33(12):55-58.An Ting，Liu Shanghe.Modeling for electromagnetic interaction by the BLT equation［J］.High Voltage Engineering，2007，33(12):55-58.(in Chinese)

［6］ 高雪莲，张晓宇，赵磊，等.基于BLT 方程的复杂线缆网络电磁干扰响应求解［J］.科学技术与工程，2015，15(5):248-252.Gao Xuelian，Zhang Xiaoyu，Zhao Lei，et al.Analysis of electromagnetic interference by using the BLT equation on the complex cable network［J］.Science Technology and Engineering，2015，15(5):248-252.(in Chinese)

［7］ Magdowski M，Ladbury J，Holloway C，et al.Measurement of the stochastic electromagnetic field coupling to an unshielded twisted pair cable［C］//Proceedings of the 2014 International Symposium on Electromagnetic Compatibility.Gothenburg，Sweden，2014:659-664.

［8］ Paul C R.Introduction to electromagnetic compatibility［M］.New York:John Wiley ＆Sons，2006:34.

［9］ Tesche F M，Ianoz M，Karlsson T.EMC analysis methods and computational models［M］.New York:John Wiley ＆Sons，1976:339-340.