无刷直流电动机不同PWM 调制方式研究

姚绪梁，张 燕，江晓明，常英健

(哈尔滨工程大学，哈尔滨150001)

0 引 言

无刷直流电动机输出转矩大、调速控制方便、动态响应迅速、可靠性高，因此应用越来越广泛［1-2］。但是它的转矩脉动问题限制了其进一步发展。此外，转矩脉动是电机产生振动与噪声的重要原因。因此，分析研究无刷直流电动机的转矩脉动具有重要意义。

文献［3］指出换相过程中由于关断相电流下降速率与导通相电流上升速率不一致，存在换相转矩脉动，但脉冲宽度调制(以下简称PWM)的影响未考虑。文献［4 -6］分析了PWM 调制方式对无刷直流电动机换相转矩脉动的影响，并未从原理上进行分析，且还应考虑换相过程中关断相与导通相电流变化率不一致的问题。

本文从非换相与换相过程出发，考虑了换相中关断相电流下降速率与导通相电流上升速率不一致，并在此前提下，详细分析了5 种不同PWM 调制方式下的转矩脉动，通过仿真研究及原理分析，验证了理论推导的正确性。

1 无刷直流电动机数学模型

以三相六状态两两工作方式为例，无刷直流电动机运行时，每个状态有60°电角度，存在非换相与换相运行过程［7］。其等效电路如图1 所示，三相端电压方程:

式中:UA，UB，UC为定子各相绕组电压;iA，iB，iC为定子各相绕组电流;eA，eB，eC为定子各相绕组反电势;L，R 为定子各相绕组等效电感、电阻;Un为中性点对地电压。

由电机理论得电磁转矩方程:

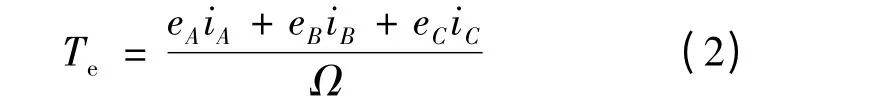
式中:Te为电磁转矩;Ω 为机械角速度。

电机运行在三相六状态两两工作方式下，HONLPWM(上桥臂恒通，下桥臂PWM)，HPWM - LON(上桥臂PWM，下桥臂恒通)，ON -PWM(前60°恒通，后60°PWM)，PWM -ON(前60°PWM，后60°恒通)及HPWM-LPWM(上下桥臂均PWM)为5 种常用的PWM 调制方式［8-9］，其中前4 种称为单斩方式，后一种称为双斩方式。

2 非换相过程转矩脉动

在非换相运行过程，定子绕组两相导通，只有两相中有电流。由于PWM 调制的影响，相电流存在持续波动［10］。以AB 相绕组导通为例，分析A 相电流。在一个PWM 周期T 内，设在t0～t1区间，PWM调制导通，S=1，相电流从I1增加到I2;在t1～t2区间，PWM 调制关断，S =0，相电流从I2减小到I1。其中T =t2-t0为PWM 开关周期，S 为开关量。S可用D 来表示，D 为PWM 占空比。

5 种方式在开关管调制导通时电流回路一致，均为VT1，VT6 导通，区别在于调制关断时续流回路不一致。由于4 种单斩方式开关管调制关断时均为开关管与二极管导通，其过程等效，故只需分析一种，以HON -LPWM 方式为例;而双斩方式为两个二极管导通，需单独讨论。

2.1 HON-LPWM 调制方式

VT1 管进行PWM 调制，VT6 管恒通。VT1 管调制关断时VD4，VT6 导通。端电压方程:

eA= -eB=E，iA+iB=0，忽略电阻R，由式(3)得:

从而:

电流波动:

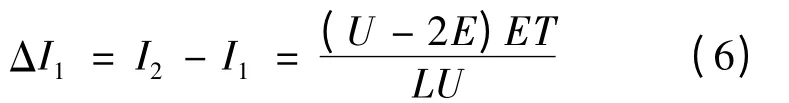
所以非换相过程单斩方式下电磁转矩脉动:

2.2 HPWM-LPWM 调制方式

VT1 管，VT6 管均PWM 调制。VT1 管，VT6 管调制关断时VD3，VD4 导通。端电压方程:

同理解得电流波动:

所以非换相过程双斩方式下电磁转矩脉动:

由式(7)和式(10)比较单斩和双斩方式下非换相过程电磁转矩脉动:

由于单斩方式的开关管调制关断时开关管与二极管导通续流，与二极管相连的定子绕组中的电感作为储能元件放电;而双斩方式的两个二极管导通，与之相连的两个定子绕组中的电感作为储能元件同时放电，直流电源吸收能量，使得其放电更快，电流下降更快，电流波动更大，转矩脉动因此更大。与上述推导结论一致。所以，在非换相过程，单斩方式较双斩方式有较小的转矩脉动。

3 换相过程转矩脉动

不同PWM 方式在上、下桥臂换相时续流回路不同，产生的转矩脉动也不同，分为上、下桥臂换相讨论。双斩方式需单独考虑［11-12］。

换相前的稳态转矩:

3.1 上桥臂换相

以AC 相换相到BC 相为例，电流的转换通过关断VT1，导通VT3 完成。C 相作为非换相相，电磁转矩与非换相电流成正比，其方程:

高速运行下，电源电压小于4 倍反电势幅值。以换相时刻作为0 点，A 相电流下降快，B 相电流上升慢，使得C 相电流有波动，从而产生换相转矩脉动。最大转矩脉动在A 相电流降为0 时取得。

不同PWM 方式在开关管调制导通时电流回路一致，如图2(a)所示，区别在于开关管调制关断时续流回路不一致。其中HON-LPWM 和ON-PWM续流回路相同，HPWM -LON 和PWM -ON 续流回路相同。

3.1.1 HON-LPWM 和ON-PWM 方式

VT2 管进行PWM 调制，VT3 管恒通。VT2 管调制关断时电流回路如图2(b)所示。三相端电压方程:

由式(13)解得三相电流方程:

A 相电流降为0 的时间:

B 相电流上升到稳定值I 的时间:

总的换相时间:

在A 相电流降为0 时刻，C 相电流:

此时的电磁转矩:

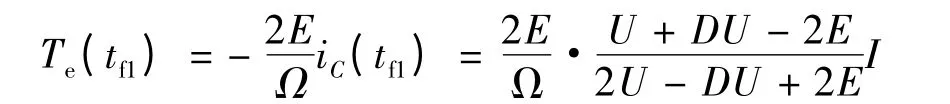
所以上桥臂换相HON -LPWM 和ON - PWM方式下的电磁转矩脉动:

3.1.2 HPWM-LON 和PWM-ON 方式:

VT2 管恒通，VT3 管进行PWM 调制。VT3 管调制关断时电流回路如图2(c)。三相端电压方程:

同样的方法解得:

所以上桥臂换相HPWM -LON 和PWM - ON方式下的电磁转矩脉动:

3.2 下桥臂换相

以AB 相换相到AC 相为例，电流的转换通过关断VT6，导通VT2 完成。A 相作为非换相相，电磁转矩与非换相电流成正比，其方程:

以换相时刻作为0 点，B 相电流下降快，C 相电流上升慢，A 相电流存在波动，从而产生换相转矩脉动。最大转矩脉动在B 相电流降为0 时取得。

不同PWM 方式在开关管调制导通时电流回路一致，如图3(a)所示，区别在于调制关断时续流回路不一致。其中HON-LPWM 和PWM-ON 续流回路相同，HPWM-LON 和ON-PWM 续流回路相同。

3.2.1 HON-LPWM 和PWM-ON 方式

VT2 管进行PWM 调制，VT1 管恒通。VT2 管调制关断时电流回路如图3(b)所示。三相端电压方程:

同样的方法解得:

所以下桥臂换相HON -LPWM 和PWM -ON 方式下的电磁转矩脉动:

3.2.2 HPWM-LON 和ON-PWM 方式

VT2 管恒通，VT1 管进行PWM 调制。VT1 管调制关断时电流回路如图3(c)所示。三相端电压方程:

同样的方法解得:

所以下桥臂换相HPWM -LON 和ON -PWM方式下的电磁转矩脉动:

3.3 HPWM-LPWM 方式

双斩方式上、下桥臂均调制，在上、下桥臂换相时效果一样，故只分析上桥臂换相过程。仍以AC导通换相到BC 导通为例。则双斩方式VT2 管，VT3 管均进行PWM 调制。

VT2，VT3 管调制导通时电流回路仍如图2(a)所示，调制关断时电流回路如图4 所示。

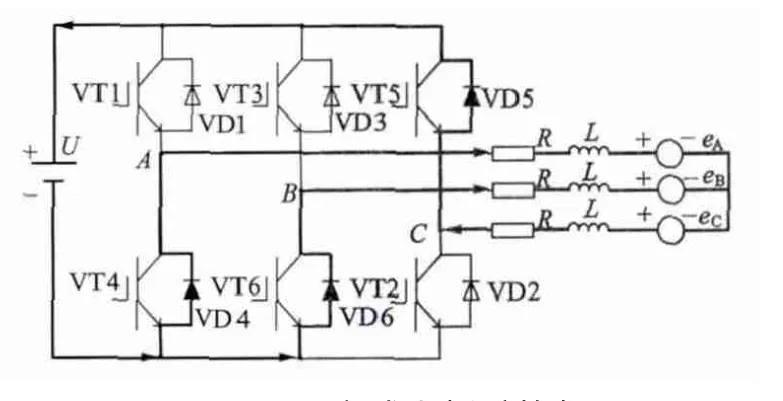
图4 HPWM-LPWM 方式上桥臂换相VT2，VT3管调制关断电流流向图

三相端电压方程:

同样的方法解得:

所以HPWM-LPWM 方式下电磁转矩脉动:

由以上分析，比较上桥臂换相转矩脉动:

同理，比较下桥臂换相转矩脉动:

所以ΔTH2＜ΔTH1＜ΔTH3，ΔTL1＜ΔTL2＜ΔTH3。由上述比较可得PWM-ON 方式有最小的换相转矩脉动。

由于HPWM - LPWM 方式在开关管调制关断时两个电流回路均为二极管导通向电源回馈能量，其电流下降最快，电流波动最大，转矩脉动也最大;而PWM-ON 方式在某一桥臂换相时保证了另一桥臂的开关管恒通，避免了电流回路里两个二极管导通向电源回馈能量现象的发生，因此理论上其电流波动最小，转矩脉动也最小;其它三种单斩方式在某桥臂换相开关管调制关断时有一个电流回路存在两个二极管导通向电源回馈能量的现象，其电流及转矩脉动较小。因此原理上PWM-ON 方式有最小的换相转矩脉动，HPWM -LPWM 方式有最大的换相转矩脉动。原理分析与上述公式推导结论一致。

4 仿真结果及分析

在MATLAB/Simulink 下搭建无刷直流电动机仿真模型。仿真所用电机参数:额定功率3.7 kW，电源电压300 V(DC)，额定转速1 500 r/min，极对数p=4，电感0.188 4 mH，磁链大小为0.148 Wb，仿真中所加负载为TL=10 N·m。

图5 为5 种不同PWM 调制方式在一个周期内的转矩波形图。设以AB 相导通作为一个周期6 个状态的起始状态，则图5 中出现的6 个尖峰分别对应上、下桥臂换相。

由图5 可知，在非换相过程，4 种单斩方式转矩脉动大致相等;在上桥臂换相过程，HON-LPWM 和PWM-ON 方式转矩脉动较小;在下桥臂换相过程，HPWM - LON 和PWM - ON 方式转矩脉动较小;HPWM-LPWM 无论在非换相还是换相过程，转矩脉动都较大，且谐波较大。综合上述分析可得PWM-ON 方式有最小的转矩脉动。与理论分析结果一致。

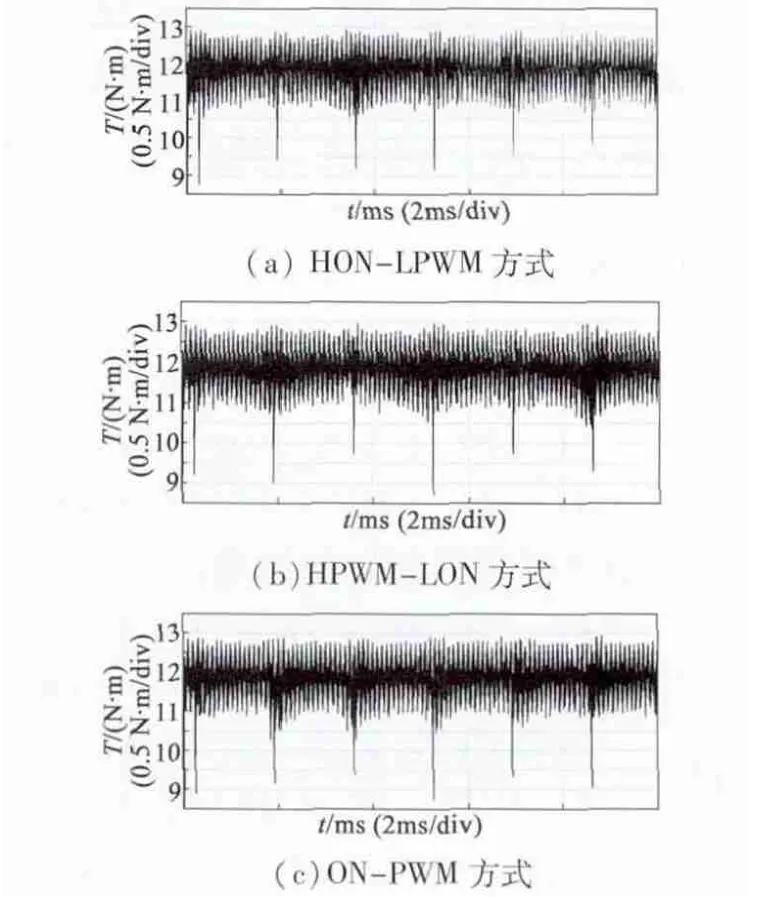
图5 5 种PWM 方式下电磁转矩仿真波形图

5 结 语

本文从无刷直流电动机运行中的定子电流的非换相和换相过程出发，通过理论的公式推导，分析了HON-LPWM，HPWM-LON，ON-PWM，PWM-ON和HPWM-LPWM 5 种常用PWM 调制方式对无刷直流电动机转矩脉动的影响，得出采用PWM -ON方式可使转矩脉动最小。在此基础上进行了原理分析，分析结果与公式推导结论一致。对无刷直流电动机在不同调制方式下进行了仿真研究，仿真结果验证了理论分析的正确性。

［1］ 贡俊，陆国林.无刷直流电机在工业中的应用和发展［J］.微特电机，2000，28(5):15 -19.

［2］ XIA Chang -liang，WANG Ying -fa，SHI Ting -na.Implementation of finite-state model predictive control for commutation torque ripple minimization of permanent - magnet brushless DC motor［J］. IEEE Trans. on Industrial Electronics，2013，60(3):896-905.

［3］ CARLSON R.Analysis of torque ripple due to phase commutation in brushless dc machines［J］.IEEE Trans on. Industrial Applications，1992，28(3):632 -638.

［4］ SALAH W A，ISHAK D，HAMMADI K J.PWM switching strategy for torque ripple minimazation in BLDC motor［J］.Journal of Electrical Engineering，2011，62(3):141 -146.

［5］ 张相军，陈伯时.无刷直流电机控制系统中PWM 调制方式对换相转矩脉动的影响［J］.电机与控制学报，2003，7(2):87 -91.

［6］ 贺安超，刘卫国，郭志大.无刷直流电动机斩波方式与电磁转矩脉动关系［J］.微特电机，2010，28(5):12 -15.

［7］ SHENG Tian-tian，WANG Xiao-lin，SHAN Tao.A new method to reduce both conduction and commutation torque ripple for BLDC machines［C］//17th ICEMS，2014:2975 -2980.

［8］ CHUANG H S，Yu-LungKe.Analysis of commutation torque ripple using different PWM modes in BLDC motors［C］//IEEE Industrial ＆Commercial Power Systems Technical Conference，2009:1 -6.

［9］ 周美兰，高肇明，吴晓刚，等.五种PWM 方式对直流无刷电机系统换相转矩脉动的影响［J］.电机与控制学报，2013，17(7):15 -21.

［10］ 贺虎成，刘卫国，郎宝华.开关频率对无刷直流电机转矩脉动的影响分析［J］.微电机，2008，41(7):1 -5.