电动汽车用永磁同步电机滑模预测控制

符晓玲，刘旭东

(1.昌吉学院，昌吉831100;2.山东大学，济南250061)

0 引 言

永磁同步电动机(以下简称PMSM)具有功率密度大，效率高、可靠性好等特点，在电动汽车应用领域存在巨大的发展潜力［1］。根据永磁体的放置方式不同，PMSM 分为内置式PMSM 和表面式PMSM。表面式PMSM 制造工艺简单、成本低，内置式PMSM因具有凸极效应而产生磁阻转矩，使其具有更宽的调速范围，目前应用于电动汽车驱动的PMSM 以内置式为主［2］。在基速以下，常用的电动汽车用PMSM 矢量控制方法包括最大转矩电流比控制和id=0控制。最大转矩电流比方法能保证系统电流的最大利用，但存在d 轴电流和q 轴电流的耦合，运行速度较慢，降低了系统的动态性能［3］。因此，本文采用id=0 的控制方法，只需要控制q 轴电流便可实现电机的控制，该方法由于没有直轴分量，损失了磁阻转矩，但是当电机运行于中低速范围时，仍能保持较高的运行效率。

另外，电动汽车是一类异常复杂且难以控制的系统，其行驶工况复杂多变、随机性强，而且对动、稳态性能指标要求极为苛刻，再加上PMSM 本身的多变量、强耦合、非线性等，传统的PI 的矢量控制方法难以满足电动汽车驱动系统的性能要求。因此，研究PMSM 的高性能转速和转矩控制具有重大的现实意义。近年来，一些先进的控制策略已逐步用在了PMSM 的转速和电流控制中，如反馈线性化［4］、滑模控制［5］、自适应控制［6］、无源性控制［7］、智能控制［8］、反步控制［9］、预测控制［10］等被应用到PMSM控制系统中，并取得了大量的研究成果。

模型预测控制作为一种新的控制方法，利用系统的输入输出数据预测未来时刻的输出，再通过优化含有输出变量和参考轨迹的目标函数，得到预测控制律，具有控制效果好、鲁棒性强、对模型精确性要求不高等优化，得到越来越多的研究人员的重视。目前已应用在机器人、电机、功率变换器等控制领域［11-13］。同样，模型预测控制方法在PMSM 控制中也证明了其有效性，文献［14］中详细介绍了三种PMSM 电流预测控制方法并做了比较;文献［15］提出了基于自动微分理论的PMSM 电流预测控制，将PMSM 的模型按泰勒级数展开，通过计算泰勒级数灵敏度，实现模型预测控制;文献［16 -17］提出了基于无差拍算法的电流环预测控制方法，文献［17］中并引入了鲁棒电流控制算法，提高系统的抗扰动性能。目前在PMSM 的预测控制方法中，大多是针对电流环的预测控制，或者是将电流环和转速环统一建模，采用非级联结构的预测控制，而针对转速环的预测控制方法较少，文献［18］中在转速环和电流环分别采用模型预测控制，并在转速环中引入了干扰模型，提高了系统抗扰性能;文献［19］提出了基于预测函数方法的PMSM 转速环控制，但是为了提高抗扰动性能，引入扩展状态观测器来观测扰动量，并采用前馈补偿的方法设计了补偿控制器。

本文在PMSM 模型预测控制中，结合滑模控制的强鲁棒性，提出了一种新型的基于滑模预测控制［20-21］的PMSM 转速跟踪控制方法。目前该方法已应用在三相变换器、伺服系统、高速飞行器等领域［22-24］。通过建立滑模预测模型、反馈校正、滚动优化等，得到滑模预测控制器，即最终的q 轴电流参考值。最后，通过仿真证明了该方法的有效性，结果表明，通过与传统的PI 控制方法相比较，该方法具有更好的转速跟踪性能和抗扰动性，适用于电动汽车驱动系统等负载转矩多变的情况。

1 PMSM 的滑模预测模型

PMSM 的矢量控制通常采用转速环和电流环级联的控制结构，本文主要研究基于滑模预测控制方法的转速环控制问题。

1.1 PMSM 的数学模型

为了建立滑模预测模型，首先需建立PMSM 的数学模型。按转子磁场定向理论，PMSM 在dq 同步旋转坐标系下的数学模型可表示:

式中:Ld和Lq为d-q 同步旋转坐标系下的定子电感;id，iq，ud，uq分别为d-q 坐标系下的定子电流和电压;Rs为定子电阻;p 为极对数;ω 为转子机械角速度;Φ 为永磁体产生的磁链;J 为转动惯量;T 为电磁转矩;TL为负载转矩;b 为摩擦系数。

对于PMSM，采用id=0 的控制方法，由式(1)的第三式和式(2)得:

将负载转矩作为扰动变量，采用零阶保持器方法，将式(3)离散化得:

令e(k)=ω(k)-ωd(k)，其中，ωd(k)为给定转速:

1.2 PMSM 的滑模预测模型

根据滑模控制理论，控制器的设计包括:(1)寻找一个具有期望性能的滑模面;(2)构造合适的控制律，使得系统误差状态能够到达滑模面，并在之后保持在滑模面上，首先定义包含电机转速误差的切换函数:

令u(k)=iq(k)，由式(6)和式(8)得:

由此可得经p 步预测后的模型:

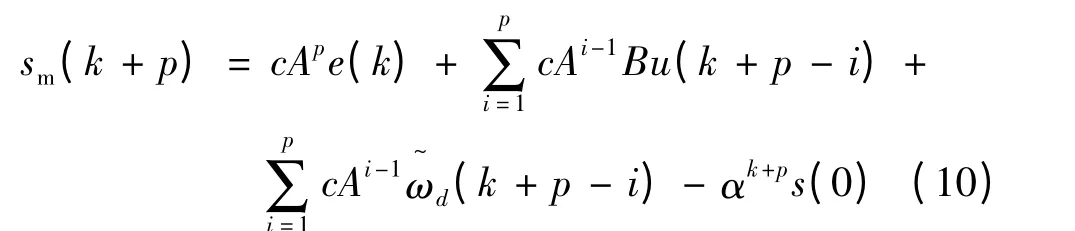
同理可得在k-p 时刻预测k 时刻的模型:

2 PMSM 的滑模预测控制器设计

基于上一节中建立的PMSM 滑模预测模型，下面将根据预测控制理论，通过反馈校正、滚动优化、以及设计的参考轨迹，求得最终的电机转速跟踪控制器。

2.1 反馈校正

考虑到实际电机模型中存在的非线性，参数时变以及外部干扰等，使得预测模型与实际的电机输出有一定的误差，利用s(k)与smp(k|k -p)的差值对k+p 时刻的滑模预测输出值sm(k +p)进行反馈校正，经过校正后的滑模预测模型输出:

式中:ξp为反馈校正系数。

2.2 参考轨迹

通过设计参考轨迹，使得系统状态沿着期望的轨迹达到设定的转速值，取参考轨迹:

式中:0 ＜β ＜1，sd为切换函数期望值，sd=0，从而滑模预测参考轨迹:

2.3 滚动优化

为了实现电机转速的快速跟踪控制，定义包括参考轨迹与预测模型误差，以及转速环控制量u(k)的性能指标函数:

式中:N 和M 分别为预测时域和控制时域，本文中，取N=6，M=1;λj为权重系数。根据文献［20］，通过对性能指标Ja最小化，可求得PMSM 转速环的滑模预测控制器:

其中:

3 仿真结果

为了验证本文设计的PMSM 滑模预测控制器的有效性，在MATLAB 下建立PMSM 控制系统的仿真模型，PMSM 的参数如表1 所示。

表1 PMSM 的参数

在滑模预测控制中，取采样时间Ts=0.2 ms，预测时间T=1 ms，λ1=0.95，α=0.95，A =0.998 8，B=0.744 5。图1 为200 rad/s，负载转矩20 N·m，取不同的β 值时的转速响应曲线。从图1 中看出，β值越小，电机转速响应越快，但过快的响应速度会使转速产生超调。

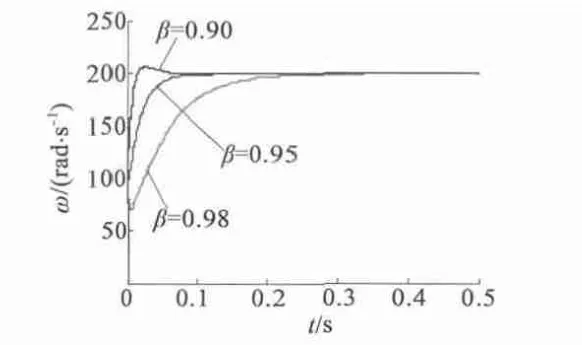
图1 不同β 值时的转速响应曲线

为了验证本文提出的滑模预测控制方法的有效性，将其与传统的PI 矢量控制方法相比较，两种方法取同样的限幅值，电流环采用相同的PI 参数，两种方法都达到较好的控制性能，在滑模预测控制中取β=0.95。图2 为给定电机转速为200 rad/s，负载转矩为20 N·m，两种方法对应的转速响应曲线。

图3 为滑模预测控制方法对应的dq 轴电流响应曲线。从图2 中可以看出，采用滑模预测控制方法超调量小，且能够更快地达到期望转速。

图3 电机起动时dq 轴响应曲线

为了验证该方法的鲁棒性，电机稳定运行在200 rad/s，在t=0.5 s 时，负载转矩由20 N·m 突变为25 N·m，图4 为电机负载转矩突变时，PI 控制和滑模预测控制两种方法的转速变化曲线，图5 为采用滑模预测控制方法对应的dq 轴电流变化曲线。

由图5 中可以看出，电机负载转矩突然增大时，对应的dq 轴电流立即增大。与此同时，转速出现较小的波动，但是与PI 控制方法相比，采用滑模预测控制方法，转速恢复时间更快，能够快速地消除负载变化的影响，具有更强的抗负载扰动性能。而采用PI 控制时，转速恢复慢，不利于电动汽车等负载转矩频繁变化且对动态性能要求高的场合。

图2 ～图5 的仿真结果表明，相比与传统的PI控制方法，本文提出的PMSM 滑模预测控制方法具有更好的转速响应性能和抗扰动性能。

4 结 语

本文提出了一种基于滑模预测控制方法的电动汽车用PMSM 的转速跟踪控制方法，用于PMSM 的转速环控制，通过建立基于速度误差的滑模预测模型，然后根据预测控制理论，经过反馈校正和滚动优化，求得电机转速控制器。从仿真结果可以看出，本文设计的滑模预测控制器能够快速地跟踪电机期望转速，且具有较强的鲁棒性能，可有效减小电机负载变化对电机性能的影响，进而有助于提高电动汽车驾乘的舒适性和动态响应性能。

［1］ EHSANI M，GAO Y M，GAY S E，et al.现代电动汽车、混合动力电动汽车和燃料电池车——基本原理、理论和设计［M］.2 版.倪光正，倪培宏，熊素铭，译.北京:机械工业出版社，2012.

［2］ 陈丹亚，贾要勤，杨仲庆.电动车驱动用IPM 永磁同步电动机控制方法综述［J］.微特电机，2010，38(2):44 -48.

［3］ 电动车用PMSM 的快速转矩电流响应控制方法［J］. 微特电机，2015，43(1):54 -57.

［4］ GRCAR B，CAFUTA P，ZNIDARIC M. Nonlinear control of synchronous servo drive［J］. IEEE Trans. on Control Systems Technology，1996，4(2):177 -184.

［5］ 张碧陶，皮佑国.基于分数阶滑模控制技术的永磁同步电机控制［J］. 控制理论与应用，2012，29(9):1193 -1197.

［6］ LI S H，LIU Z G. Adaptive speed control for permanent -magnet synchronous motor system with variations of load inertia［J］.IEEE Trans. on Industrial Electronics，2009，56(8):3050 -3059.

［7］ PETROVIC V，ORTEGA R，STANKOVIC A M. Interconnection and damping assignment approach to control of PM synchronous motors［J］. IEEE Trans. on Control Systems Technology，2001，9(6):811 -820.

［8］ YANG Y，VILATHGAMUWA D M，RAHMAN M A. Implementation of an artificial-neural-network-based real -time adaptive controller for an interior penmanent magnet motor drive［J］. IEEE Trans. on Energy Conversion，2003，39(1):96 -104.

［9］ YU J P，GAO J W.Adaptive fuzzy tracking control for a permanent magnet synchronous motor via backstepping approach［J］. Mathematical Problems in engineering，2010，17(4):242 -256.

［10］ BLOLGNANI S，BOLOGNANI S，PERETTI L.Design and Implementation of Model Predictive Control for Electrical Motor Drives［J］.IEEE Trans. on Industrial Electronics，2009，56(6):1925-1936.

［11］ SUNG J Y，YOON H C，JIN B P. Generalized predictive control based on self - recurrent wavelet neural network for stable path tracking of mobile robots:adaptive learning rates approach［J］.IEEE Trans. on Circuits and Systems，2006，53(6):1381 -1394.

［12］ JAROSLAW G，HAITHAM A R.Speed sensorless induction motor drive with predictive current controller［J］. IEEE Trans. on Industrial Electronics，2013，60(2):609 -709.

［13］ 杨勇，阮毅，叶斌英.三相并网逆变器无差拍电流预测控制方法［J］.中国电机工程学报，2009，29(33):40 -46.

［14］ MOREL F，LIN -SHI X F，RETIF J M. A comparative study of predictive current control schemes for a permanent-magnet synchronous machine drive［J］.IEEE Trans. on Industrial Electronics，2009，56(7):2715 -2728.

［15］ 高丽媛，卢达，赵光宙.应该自动微分的永磁同步电机预测控制［J］. 电机与控制学报，2012，16(10):38 -43.

［16］ 王宏佳，徐殿国，杨明.永磁同步电机改进不差拍电流预测控制［J］. 电工技术学报，2011，26(6):39 -45.

［17］ 牛里，杨明，刘可述. 永磁同步电机电流预测控制算法［J］.中国电机工程学报，2012，32(6):131 -137.

［18］ CHAI S，WANG L P，ROGERS E.A cascade MPC control structure for a PMSM with speed ripple minimization［J］.IEEE Trans.on Industrial Electronics，2013，60(8):2978 -2987.

［19］ LIU H X，LI S H.Speed control for PMSM servo system using predictive functional control and extended state observer［J］. IEEE Trans. on Industrial Electronics，2012，59(2):1171 -1183.

［20］ XIAO L F，SU H Y，CHU J. Sliding mode prediction tracking control design for uncertain systems［J］.Asian Journal of Control，2007，9(3):317 -325.

［21］ HOUDA B M，SAID N A. Discrete predictive sliding mode control of uncertain systems［J］. International Multi -Conference on Systems，Signals and Devices，2012:1 -6.

［22］ CURKOVIC M，JEZERNIK K，HORVAT R. FPGA -based predictive sliding mode controller of a three - phase inverter［J］.IEEE Trans. on Industrial Electronics，2013，60(2):3050 -3059.

［23］ 尹洋，夏立，宋立忠.网络直流伺服电机滑模预测控制［J］.电力自动化设备，2011，31(6):65 -69.

［24］ 高海燕，蔡远利.高超声速飞行器的滑模预测控制方法［J］.西安交通大学学报，2014，48(1):67 -72.