三自由度混合磁轴承转子位移智能自检测

朱志莹，孙玉坤，李祖明，周云红，王正齐

(南京工程学院，南京211167)

0 引 言

三自由度混合磁轴承(以下简称3 - DOF -HMB)集径向磁轴承和轴向磁轴承双重功能，同时利用永磁体提供偏置磁通，具备结构紧凑、体积小、功耗低等优点［1-5］，在高速、超高速场合中具备独特应用价值［6］。

位移检测环节是3 -DOF-HMB 系统的重要组成部分，位移信息实时精确获取直接决定其稳定悬浮功能的实现。目前国内外实际应用中多是直接利用电涡流式、电感式、光电式及电容式等各种位移传感器，这些传感器的存在，不仅使系统结构复杂，轴向尺寸变大，降低系统的动态性能;而且由于机械结构的限制，位移传感器与磁轴承不能共点安装，导致系统的控制方程彼此耦合，大大增加了控制系统设计的复杂性;同时，3 -DOF -HMB 采用差动检测需要6 个位移传感器，每个传感器价格昂贵，且易受环境干扰，致使磁轴承系统的总体价格高，可靠性低。这些问题都大大限制了基于位移传感器检测的3 -DOF-HMB 系统的实际推广应用［7］。因此，探索无位移传感器的3 -DOF -HMB 转子位移自检测方法，对简化系统结构、降低成本、提高系统可靠性具有重要意义。

为实现磁轴承转子位移自检测，国内外学者相继提出了高频信号注入法［8］、凸极追踪［9］、占空比补偿［10］、状态观测［11］、卡尔曼滤波器［12］等多种方法。这些方法各有特点，其中高频信号注入、凸极追踪和占空比补偿法需要附加电路和特殊信号处理技术才能实现位移的估计;而状态观测、卡尔曼滤波等方法依赖精确模型，且对控制器要求非常高，加之3 -DOF-HMB 本质非线性和参数不确定性，这些方法的实际应用效果不理想，存在鲁棒性差、动态性能低和信噪比不高等问题。为此，部分学者提出利用神经网络来实现位移自检测［13］，但是神经网络还存在依赖样本数据、易陷入局部极值等缺陷。近年来，由Vapnik V 等人［14］提出的支持向量机(support vector machine，SVM)是继神经网络之后的新型机器学习方法，该方法基于统计学习理论，具有不依赖对象模型，结构简单，泛化能力强等优点，非常适合解决小样本、非线性及高维函数拟合问题。最小二乘SVM 将标准SVM 的学习问题转化为求解一组线性方程，从而进一步提升了算法速度［15-16］。目前已被广泛用于模式识别［17］与时间序列预测［18-20］，并在磁轴承位移预测建模［21］与电机转子位置估计［22-23］中也得到研究，且获得了较高的预测精度。

本文从3 -DOF-HMB 基本工作原理和精确数学模型出发，研究了基于最小二乘SVM 的3 -DOF- HMB 转子位移智能自检测方法。该方法通过输入输出变量确定和有效样本数据的获取，离线训练最小二乘SVM 获得3-DOF-HMB 位移自检测模型，针对模型参数选取问题，采用自适应遗传算法进行自动寻优，以提高自检测模型精度。最后通过仿真和实验对自检测模型进行研究，验证了方法的有效性。

1 3 -DOF-HMB 基本原理与数学模型

1.1 基本原理

图1 给出了3 -DOF -HMB 结构示意图，它主要由永磁体、径轴向定子、转子、径轴向控制线圈等构成。径向定子上均匀设置3 个磁极，定子铁心采用硅钢片叠压而成，永磁体采用钕铁硼制成。

工作时3 -DOF-HMB 通过调节径轴向控制线圈中的电流，改变径、轴向气隙处的磁场强度，从而在转子上产生不平衡的径向电磁力和轴向电磁力，实现对转子径向两自由度和轴向单自由度的悬浮控制。径向充磁的永磁体为径轴向悬浮力的产生提供静态偏置磁通，当径向和轴向都稳定悬浮时，转子在静态偏置磁场作用下处于参考位置。当转子因扰动而偏离参考位置时，轴向控制线圈通直流电实现转子轴向悬浮调节，沿圆周120°均匀分布的A，B，C三个径向控制线圈通以三相交流电，产生可旋转的合成磁通实现转子径向悬浮调节。

1.2 数学模型

3 -DOF-HMB 因其电磁非线性与参数不确定性，使其电磁模型难用解析表达式进行精确描述。传统基于泰勒展开在平衡位置附件线性化的模型难以反映磁轴承大气隙范围内的实际动态特性。三维有限元法能考虑磁饱和与端部漏磁等实际特性，可准确获得电磁力关于电流、位移的非线性关系，是目前磁轴承电磁分析计算较为实用的方法。本文为此首先利用三维有限元法测定不同位移与电流下悬浮力。图2 以轴向为例，给出了悬浮力Fz与位移z，电流iz之间的关系。

为使悬浮力模型充分考虑大气隙范围内非线性特性，进一步采用变刚度系数法获取不同位移和电流下的位移刚度kz和电流刚度kiz，然后基于变刚度系数kz和kiz构建大气隙范围内悬浮力模型［24］:

式中:Fx，Fy，Fz为转子三自由度悬浮力;x，y，z 为转子三自由度偏心位移;kdx，kdy，kdz为三自由度位移刚度;kix，kiy，kiz为三自由度电流刚度;ix，iy，iz为悬浮控制电流。

其中ix，iy由三相交流电iA，iB，iC变换得到:

在非线性电磁力基础上，根据转子动力学理论可知3 -DOF-HMB 转子运动方程:

式中:m 为转子质量，fx，fy和fz为转子三自由度所受外部干扰力。

式(1)～式(3)构成3 -DOF-HMB 数学模型，由于该模型考虑了转子偏心与电流的影响，因而能够较好地反映出3 -DOF-HMB 在大气隙范围内非线性悬浮力-电流-位移关系。

2 3 -DOF-HMB 转子位移自检测建模

2.1 SVM 回归建模原理

已知输入输出样本数据(x1，y1)，(x2，y2)，…，(xn，yn)，根据最小二乘SVM 基本理论，其拟合问题可以转化为对式(4)求解:

式中:γ 为正则化参数;ei表示第i 个样本的误差。进而用拉格朗日法求解式(4)优化问题:

式中:αi是拉格朗日乘子。根据优化条件，对式(5)求偏导，将优化问题转化为求解线性方程:

式中:y=［y1，…，yn］T，1ν=［1，…，1］T，α=［α1，…，αn］T，K =［kij］n×n，kij=K(xi，xj)，I是单位矩阵，K(·)为核函数，此处选用径向基函数:

式中:σ 为核宽度。相应地得到最小二乘SVM 的非线性模型:

2.2 基于SVM 的位移自检测模型

基于最小二乘SVM 的3 -DOF -HMB 转子位移自检测，就是利用式(8)为3 -DOF -HMB 建立一个有效的映射结构，通过磁轴承电气信号(电压或电流)的检测，所建立的SVM 自检测模型能够正确估计出转子位移。3 -DOF -HMB 是通过调节控制电流实现对转子位移的控制，因此可以初步确定径向控制电流iA，iB，iC和轴向控制电流iz是影响转子位移变化的主要因素，而径向控制电流iA，iB，iC可由两相静止坐标系下的电流ix，iy经C2/3变换得到。因此，最终确定最小二乘SVM 自检测模型的输入和输出为电流(ix，iy，iz)与位移(x，y，z)。另外，考虑到最小二乘SVM 多用于解决单变量回归问题，因而需要对每个自由度位移分别建立自检测模型，限于篇幅，本文以轴向位移自检测为例进行说明。

输入输出数据的获取是SVM 自检测模型建模的前提。由于3 -DOF-HMB 是一个负刚度和零阻尼系统，开环控制无法稳定工作，因此在PID 闭环控制下采集输入输出样本数据［21］。同时为了使样本能充分反映3 -DOF -HMB 的非线性，选取幅值为0.3 mm 的正弦信号叠加幅值为0.1 mm 的随机信号作为激励，其中正弦信号用于揭示系统内部非线性特性，随机信号用以模拟外部扰动;采样频率设为100 Hz，总采样时间0.5 s，共采集5 000 组样本数据。这5 000 组数据是转子偏离平衡位置±0.4 mm范围运动的数据，因此涵盖了动态起浮和稳态悬浮情况。考虑到SVM 小样本学习特点，本文对5 000组数据进行预处理，选取其中300 组作为训练集，200 组作为测试集，分别用于构建和验证SVM 自检测模型。图3 给出了轴向位移SVM 自检测模型拓扑。

2.3 自检测模型参数优化

最小二乘SVM 理论上已经证明可以在有限样本学习下任意精度地逼近高维非线性函数，然而实践表明SVM 的正则化参数γ 和核参数σ2影响模型的精度。本文为提高SVM 精度，实现3 - DOF -HMB 转子位移的高性能自检测控制，采用自适应遗传优化算法对模型参数进行自动寻优。该算法在进化过程中，变异概率和交叉概率随种群适应度自动调整，可避免传统遗传算法早熟和不易收敛等问题［25］。

针对SVM 待优化的参数，算法的适应度函数选取为实际值与模型预测值的均方误差(以下简称MSE)，其计算公式:

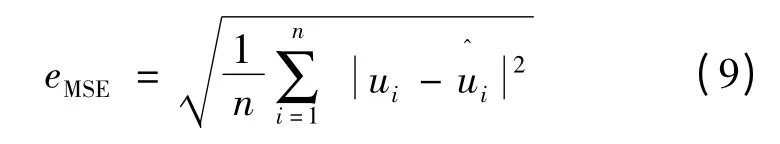
式中:ui和分别为期望输出和模型输出;n 为测试数据的总组数。

考虑到只有γ 和σ2两个参数需要优化，因而采用简洁的二进制编码方式;自适应交叉概率Pc和自适应变异概率Pm:

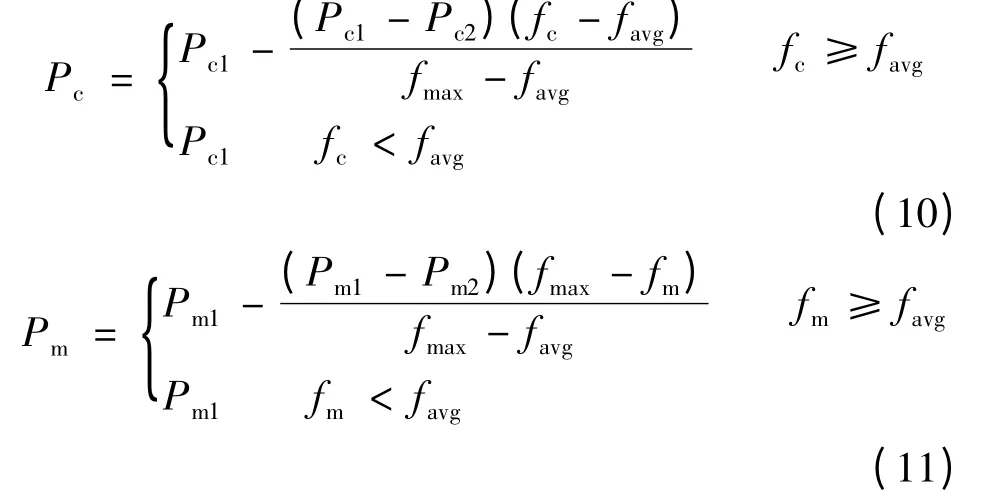
式中:Pc1=0.9，Pc2=0.6，Pm1=0.1，Pm2=0.001，fc为两交叉个体适应度较大值，fm为变异个体的适应度，favg和fmax为群体的平均适应度和最大适应度。

图4 为模型参数的优化流程，表1 给出了自适应遗传算法相关参数设置，图5 给出了自适应遗传算法优化过程中适应度随进化代数的变化曲线。

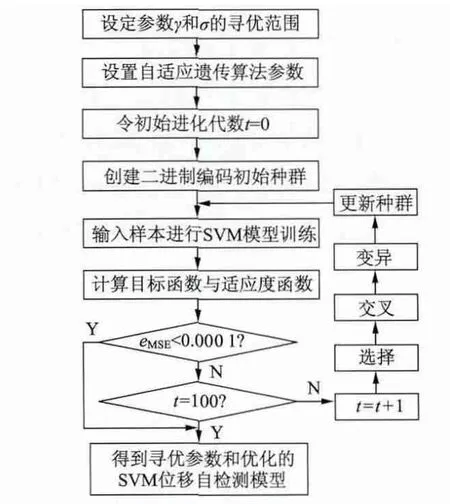
图4 自适应遗传算法优化SVM 参数流程图

图5 适应度随进化代数变化曲线

表1 自适应遗传算法参数设置

2.4 自检测模型评价

为了说明自适应遗传优化SVM 自检测模型的有效性，将其与常规遗传算法以及文献［21］中的粒子群优化算法模型进行比较。对比研究中，三种优化算法的进化代数、种群规模、终止精度以及参数γ和σ2的寻优范围均相同，如表1 所示。采用式(9)均方误差MSE 和式(12)绝对误差(以下简称AE)作为评价指标来衡量模型优劣。

式中:ui和分别是转子位移的实测值和模型输出值;n 为测试样本个数。

表2 给出了三种优化方法所获得的参数优化结果、优化时间以及MSE 性能指标。由表2 可见，本文所述自适应遗传算法优化耗时为1.299 4 s，训练误差为1.166 6 μm，测试误差为1.167 1 μm;相比常规遗传算法，优化速度提高了近10 倍，训练和测试误差降低了7 倍;相对文献［21］所提粒子群算法，优化耗时多0.2 s，但训练精度和测试精度分别提升了3 ～4 倍。

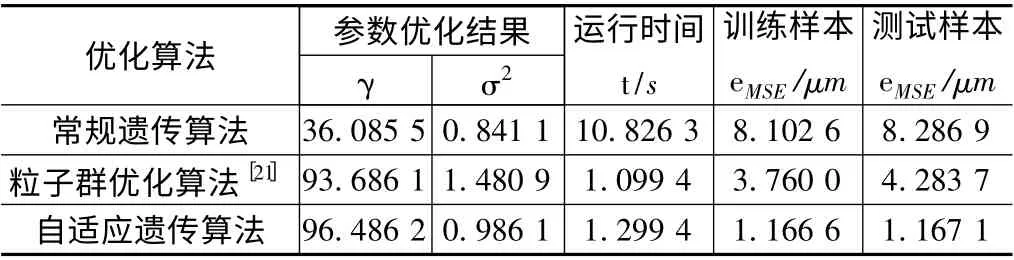
表2 参数优化结果

图6 给出了文献［21］粒子群算法和本文算法所建自检测模型误差AE 值曲线。由图6 可见，两种算法所建SVM 自检测模型的拟合和预测误差AE值均较小，这表明SVM 模型克服了神经网络的过拟合缺陷，达到了拟合和泛化能力的折中;同时，比较图6 可见，文献［21］所建自检测模型的拟合误差和预测误差的最大值分别为7 μm 和10 μm，而本文所建模型的拟合和预测误差的最大值分别降低到了1.2 μm 和1.8 μm，这进一步表明本文算法在拟合和泛化精度上的优越性。

3 转子位移自检测控制

为了验证理论分析的有效性，对所建SVM 自检测模型开展位移自检测控制仿真与实验研究。仿真和实验中，3 -DOF -HMB 相关参数详见文献［3］。图7 给出了3 -DOF -HMB 自检测控制系统框图，整个控制系统分为悬浮控制模块和自检测模块两个部分。其中自检测模块将检测到的径向三相交流电流{iA，iB，iC}经过3s/2s 变换为{ix，iy}与轴向电流iz一起输入到SVM 位移自检测模型，位移自检测模型根据输入电流信息实时准确预测出转子位移{x，y，z}，并与参考位移{x*，y*，z*}进行比较。悬浮控制模块将参考位移与自检测位移比较得到的差值送入PID 控制器，PID 控制器调节得到转子悬浮所需悬浮力指令值，再利用悬浮力模型调制出悬浮绕组电流的指令值，径向线圈电流通过2s/3s 变换后输入到电流跟踪型逆变器，轴向线圈电流送入线性功放，通过逆变器和线性功放输出控制电流，继而实现3 -DOF-HMB 转子位移自检测控制，从而避免了位移传感器的使用，达到无位移传感器运行目的。

图8 给出了3 -DOF-HMB 起浮和悬浮时轴向位移实测值、预测值与预测误差曲线。从图8(a)可以看出，基于本文所提位移自检测算法能够准确、快速预测出转子的实际位移，并最终稳定悬浮在平衡位置处。从图8(b)预测误差曲线可以看出，转子起浮阶段的预测误差比稳定悬浮阶段预测误差大，这主要是由于悬浮力建模中忽略了各自由度耦合力的影响，尤其是转子起浮时，耦合力相对较大，使位移自检测模型和实际系统存在一定的误差，同时最小二乘SVM 回归计算消耗一定时间，导致了预测位移滞后于实际位移。但是从图8 可以看出，整个过程自检测模型的最大预测误差仅为0.012 mm，远小于气隙长度0.5 mm。

图9 给出了自检测控制下3 -DOF-HMB 转子起浮过程中径向质心轨迹。从图9 可以看出，转子在初始偏心下，所提自检测方法能使转子快速稳定到平衡位置处，且转子起浮过程中，质心轨迹相对比较平滑，这表明自检测方法具有较好的起浮性能。

图10 给出了自检测控制和传统有位移传感器控制下的转子位移波形。其中图10(a)为转子轴向静态悬浮时位移波形，图10(b)为转子轴向受到冲击干扰下的位移波形，图10(c)为转子1 400 r/min时轴向位移动态实验波形。由图10 可见，在转子静态悬浮、冲击干扰和恒速旋转下，所建自检测模型输出值均能较好地跟踪位移传感器检测值，这表明本文所提自检测算法具有较高的检测精度，可为3 -DOF-HMB 转子悬浮控制提供准确的位移信息。

4 结 语

本文分析了3 -DOF -HMB 非线性电磁力特性，构建了考虑磁饱和与转子偏心的数学模型，重点研究了一种基于自适应遗传优化支持向量机的3 -DOF-HMB 转子位移智能自检测方法，并开展了对比仿真和实验研究。得到如下结论:

1)变刚度系数构建的电磁力模型能够有效表达3 -DOF -HMB 大气隙范围内非线性特性，可为SVM 位移自检测模型构建提供有效的学习样本;

2)基于支持向量机的自检测模型能够映射出输入电流与输出位移的关系;采用自适应遗传算法优化模型参数，可有效提高自检测模型的拟合和泛化精度;

3)位移自检测控制方案简化了3 -DOF -HMB检测和控制系统结构，可实现位移传感器的消去，为磁轴承的高性能控制提供了一种新的方法;

4)3-DOF -HMB 各自由度之间存在一定耦合，影响模型精度和控制效果，后续研究中需进一步考虑各自由度耦合影响，并设计相应的解耦控制策略。

［1］ 赵旭升，邓智泉，王晓琳，等. 永磁偏置磁轴承的研究现状及其发展［J］. 电工技术学报，2009，24(9):9 -20.

［2］ 孙津济，房建成，王曦，等. 一种新型结构的永磁偏置径向磁轴承［J］. 电工技术学报，2009，24(11):53 -60.

［3］ 朱熀秋，张仲，诸德宏，等. 交直流三自由度混合磁轴承结构与有限分析［J］. 中国电机工程学报，2007，27(12):77 -81.

［4］ 张云鹏，刘淑琴，李红伟，等. 基于磁路分析的轴向混合磁轴承径向承载力解析计算［J］. 电工技术学报，2012，27(5):137 -142.

［5］ 赵旭升，邓智泉，汪波. 异极性永磁偏置径向磁轴承的参数设计与实现［J］. 电工技术学报，2012，27(7):131 -138.

［6］ 戴兴建，邓占峰，刘刚，等. 大容量先进飞轮储能电源技术发展状况［J］. 电工技术学报，2011，26(7):133 -140.

［7］ 金婕，朱熀秋. 磁悬浮轴承转子位移自检测方法［J］. 微电机，2014，47(9):79 -84.

［8］ YIM J S，SUL S K，AHN H J，et al.Sensorless position control of active magnetic bearings based on high frequency signal injection with digital signal processing［C］//IEEE，Applied Power Electronics Conference and Exposition，California，USA，2004:1351 -1354.

［9］ GARCIA P，GUERRERO J M，BRIZ F，et al. Sensorless control of three- pole active magnetic bearings using saliency - tracking -based methods［J］. IEEE Transactions on Industry Applications，2010，46(4):1476 -1484.

［10］ 唐明，祝长生.基于占空比补偿的电磁轴承无传感器运行［J］. 浙江大学学报(工学版)，2013，47(8):1418-1423，1430.

［11］ DESHPANDE M，BADRILAL M.Sensorless control of magnetic levitation system using sliding mode controller［C］// International Conference on Computer Applications and Industrial Electronics，Kuala Lumpur，Malaysia，2010:9 -14.

［12］ MATSUDA K，KIJIMOTO S，KANEMITSU Y. Self - sensing three-pole magnetic bearing using a kalman filter［C］// SICE -ICASE International Joint Conference，Busan，Korea，2006:1590-1594.

［13］ SADIGHI A，KIM W J.Adaptive-neuro -fuzzy - based sensorless control of a smart -material actuator［J］. IEEE/ASME Transactions on Mechatronics，2011，16(2):371 -379.

［14］ VAPNIK V.The nature of statistical learning theory［M］. Berlin:Springer Science ＆ Business Media，2000.

［15］ SUYKENS J A，VAN GESTEL T，DE BRABANTER J，et al. Least squares support vector machines［M］. Singapore:World Scientific，2002.

［16］ VAN GESTEL T，SUYKENS J A，BAESTAENS DE，et al. Financial time series prediction using least squares support vector machines within the evidence framework［J］. IEEE Transactions on Neural Networks，2001，12(4):809 -821.

［17］ 王瑜，苑津莎，尚海昆，等. 组合核支持向量机在放电模式识别中的优化策略［J］.电工技术学报，2015，30(2):229 -236.

［18］ MÜLLER K-R，SMOLA A J，RATSCH G，et al.Predicting time series with support vector machines［M］//Artificial Neural Networks—ICANN＇97.Berlin:Springer，1997:999 -1004.

［19］ 王贺，胡志坚，仉梦林. 基于模糊信息粒化和最小二乘支持向量机的风电功率波动范围组合预测模型［J］. 电工技术学报，2014，29(12):218 -224.

［20］ CAO L J，TAY F E H. Support vector machine with adaptive parameters in financial time series forecasting［J］. IEEE Transactions on Neural Networks，2003，14(6):1506 -1518.

［21］ 朱志莹，孙玉坤.群优化支持向量机的磁轴承转子位移预测建模［J］.中国电机工程学报，2012，32(33):118 -123.

［22］ 夏长亮，贺子鸣，周亚娜，等. 基于支持向量机的开关磁阻电机转子位置估计［J］.电工技术学报，2007，22(10):12 -17.

［23］ 项倩雯，孙玉坤，嵇小辅，等. 单绕组磁悬浮开关磁阻电机无径向位移传感器控制［J］. 电工技术学报，2013，28(8):259 -267.

［24］ REN Y，FANG J. High -precision and strong -robustness control for an MSCMG based on modal separation and rotation motion decoupling strategy［J］. IEEE Transactions on Industrial Electronics，2014，61(3):1539 -1551.

［25］ 徐斌，姚缨英.自适应对偶种群遗传算法及其在电磁场优化设计中的应用［J］.电工技术学报，2013，28(3):183 -187.