基于卡尔曼滤波的超声波电动机测速算法研究

黄 帆，金 龙，徐志科，潘 鹏

(东南大学，南京210096)

0 引 言

超声波电动机，尤其是行波超声波电动机以其低速大转矩、运行无噪声、无电磁干扰和体积小等良好特性，在伺服驱动应用中得到了越来越多的关注，并取得了一定的研究成果。在超声波电动机的控制系统中，无论是使用经典的PID 控制还是现代的智能控制算法，电机转子的速度和位置是必不可少的闭环反馈量。因此，反馈量的测量精度对控制系统有着至关重要的作用。然而鉴于高精度的位置和速度传感器价格昂贵以及安装环境的限制，大多数超声波电动机伺服系统都是使用编码器来获取电机的位置信息，再通过一定的算法来得到电机的速度信息。其中用的比较多的是增量式编码器，这种编码器具有误差累积的缺点，因此只能提供一定精度的位置和速度的测量。卡尔曼滤波作为一种重要的最优估计理论，去除观测数据中的噪声还原真实数据，已广泛应用于导航、动态定位、动力及最优控制等多种动态数据处理中。在交流伺服领域，许多学者将卡尔曼滤波应用于电磁电机中，同时取得了较好的控制效果。文献［1 -2］将扩展卡尔曼滤波应用于无速度传感器的永磁同步电机控制，对电机的转速和磁链进行精确估计以提高直接转矩控制的性能。文献［3］将无迹卡尔曼滤波(UKF)原理与永磁同步电机的系统模型相结合设计出UKF 定子磁链观测器，实现永磁同步电机转子位置和转速的无传感器估计。使用无迹变换，以确定性的采样方法计算随机变量的统计特性，相比较扩展卡尔曼滤波估计精度更高，运算速度更快。文献［4］将转子电压和转子电流作为系统的输入量，估计直流电机的转速，增加了系统的鲁棒性并且精确地估计了直流电机的转速。文献［5 -6］分别运用扩展卡尔曼滤波和模糊扩展卡尔曼滤波，建立感应电机的速度和磁链观测器，类似于直流电机通过转矩和磁链来控制电机的速度，使感应电机系统表现出良好的动态性能。

然而卡尔曼滤波算法在超声波电动机的控制中应用研究很少，因此本文在研究超声波电动机测速算法的基础上，针对原有方法的不足将卡尔曼滤波理论与其相结合应用到超声波电动机测速系统中。把各种测速误差的影响看成超声波测速系统的系统误差，而编码器的分辨率、加工和安装精度等的影响作为测量误差，建立系统的动态模型。在位置差分测速的基础上，引入卡尔曼滤波以减小测量误差，提高参数测量精度，并通过仿真研究验证了该策略的有效性。

1 卡尔曼滤波

所谓滤波，实际上就是选频，即从带有多频的信号中得到想要的频率，而将不需要的频率过滤掉。滤波理论就是在对系统信号进行测量和滤频过程中，经过实践检验符合实际情况的最优方法、理论体系。卡尔曼滤波理论是20 世纪60 年代发展起来的一种现代滤波理论，它是通过一系列递归数学公式描述和推算来估计某个过程的状态。该理论之所以被广泛应用，就是因为它能够将噪声对系统状态的辨识影响降到最小。由于卡尔曼滤波器的解是递归计算的，其每一次的状态更新只需要上一次的状态估计值和最新的测量变量输入计算便可得到，不需要存储大量的数据，并且数据处理也很高效。这些优点特别适合基于微处理器的超声波电动机伺服控制，在有限的内存空间下实现电机的实时控制。

卡尔曼滤波器用(含噪声)测量变量作为反馈，从而来估计过程状态。离散卡尔滤波器则是将系统的状态方程和测量方程离散化，间隔一定的时间采样测量变量获得反馈，来估计某一时刻的状态，其离散化的状态方程由以下差分方程描述:

系统的测量方程:

式中:wk为系统的过程噪声;vk为测量噪声。卡尔曼滤波要求它们为相互独立、均值为零的白色噪声序列。过程噪声和测量噪声的方差矩阵分别为Q 和R，卡尔曼滤波中要求它们分别是已知值的非负定矩阵和正定矩阵。xk为系统的状态变量，uk为确定性输入变量，A 为状态转移矩阵，B 为可选的控制输入增益矩阵。zk为系统的测量变量，H 为状态变量xk对测量变量zk的增益。定义(^表示先验，-表示估计)为在利用第k-1 时刻和以前时刻的测量值得到的第k 时刻的先验状态估计，定义x^k 为已知测量变量zk时第k 步的后验状态估计。则离散卡尔曼滤波算法的流程如图1 所示。

图1 离散卡尔曼滤波工作原理图

在实际系统中，矩阵Q 和R 可能会随着每次迭代计算而变化。为了降低算法以及计算的复杂度，这里假设它们都为常数。在卡尔曼滤波器的构造中，状态误差协方差的初值x0，P0，R 和Q 的取值对于卡尔曼滤波器的性质会有一定的影响。如果P0取值较小，卡尔曼滤波器收敛速度会比较快。而测量噪声协方差R 一般可以通过测量得到，是滤波器的已知条件，通常我们离线获取系统的测量值以计算测量噪声协方差。比较难确定的是过程激励噪声协方差Q 的值，Q 表征了系统的统计特性，其值的大小表征着系统的动态性能，但是过程信号xk无法直接观测到，因此很难通过直接的观测量得到Q值。所以我们通常都是通过调整滤波器系数来获得更好的性能。在初始值的选择过程中，我们既要考虑收敛的快速性，又要防止卡尔曼滤波的发散，否则会对系统的控制产生不良的后果。

2 基于卡尔曼滤波的测速算法

2.1 基于卡尔曼滤波的测速系统

基于增量式编码器的测速算法大致分为三类:(1)M 算法测速，在固定的时间间隔内测量脉冲发生器所产生的脉冲数来获取速度值，这种测速算法适合中高速测量场合;(2)T 算法测速，通过测量相邻两个位置事件的时间间隔来确定被测速度，适合于低速测量场合，由于系统需要加入脉冲捕捉中断电路和计时定时电路，所以实现起来T 算法要比M算法更加复杂;(3)M/T 算法测速，综合了以上的两种方法，同时测量检测时间和在此时间内脉冲发生器所产生的脉冲数来确定被测转速。M/T 算法在高低速时测量精度均有所提高，扩大了测速的范围，但是也增加了硬件和软件实现的复杂性。从成本和实用性角度考虑，本文采用M 算法进行测速。

由于系统噪声和观测噪声的影响，M 法测速得到的速度值误差较大，因此将卡尔曼滤波引入测速算法，以抑制电机本身及编码器引起的白噪声对测速算法的影响。在超声波测速系统中，电机的位置和速度为未知量，因此把电机的位置θ、速度v 认为是状态变量，建立一个关于位置和速度的模型，从这个模型得到卡尔曼滤波器。

设超声波电动机在k 时刻的位置为θk、速度为vk，从k 时刻到k +1 时刻电机的加速度为ak，根据牛顿运动定律电机，在k+1 时刻的位置θk-1和速度vk-1可分别表示:

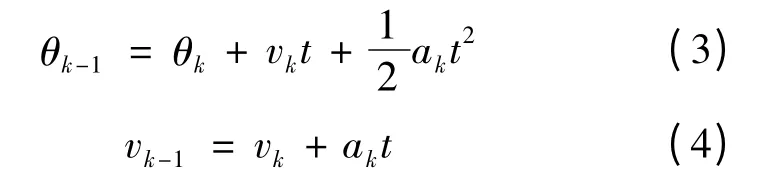
由于系统在运行过程中速度会有一定的波动，甚至有时会出现大的波动，因此电机速度的变化在实际运行中并无固定的规律性，这里将速度的变化率即加速度看成高斯白噪声。则状态方程可表示:

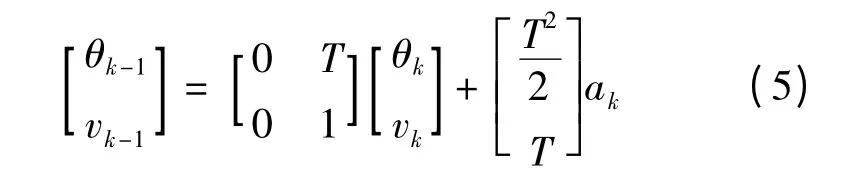
式中:ak即w 为系统的模型干扰，它符合均值为零、方差为σa的正态分布。则可得到协方差矩阵:

每隔固定的时刻，对电机的位置进行测量，则观测方程可表示:

式中:v 为系统的测量干扰，它符合均值为零、方差为σz的正态分布，且系统干扰与模型干扰为两个相互独立高斯白噪声。则可得到协方差矩阵R:

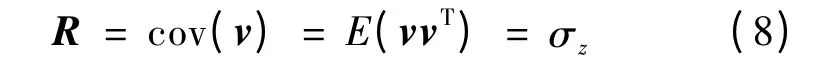
超声波电动机的卡尔曼滤波模型已经确定，要想实现图1 中公式的递推，必须首先确定初值，P0。对于初值，P0的确定，至今尚未有成熟的方法，大多数情况下，都是根据经验利用一期的观测信息确定状态向量中的相对位置信息θ0，再利用相邻两期的相对位置确定角速度v0，这样便得到了滤波的初值［15］。P0是x0的估计误差协方差矩阵，假设的均值为μ0，则:

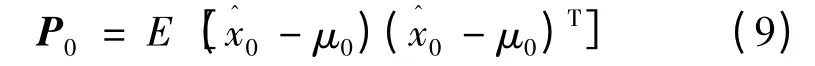
2.2 仿真设计

本文通过MATLAB 仿真来验证卡尔曼滤波器对于超声波电动机测速系统的滤波性能，其观测方程的电机位置信息由控制系统实际运行给出。实际系统的实验平台为基于TMS320F28335 的实验室自制直径为80 mm 的超声波电动机，测角系统采用雷尼绍公司SIGNUM RESM 系列圆光栅编码器，圆光栅一圈刻线数为31 488 道，经细分盒100 细分(四倍频采集方式)，每转一圈产生3 148 800 个脉冲。所以其测量分辨率Re为:

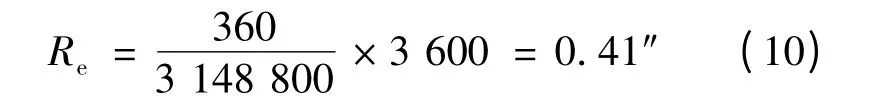
实验对象为闭环PI 控制的超声波电动机系统，由DSP 的eQEP 单元以10 Hz 的频率获取编码器发出的脉冲数以确定电机的位置，再用M 算法计算电机的速度。虽然M 算法获得的转速存在一定的误差，但是基本上能够反映电机的实际速度，因此在有限的实验条件下将M 算法获得的速度作为参考标准与卡尔曼滤波算法仿真滤波后的电机速度进行比较［9］。为了便于获取每次采样的脉冲数和电机的速度，实验平台通过SCI 模块与上位机相连接，实时的将规定数据发送给上位机，上位机将数据记录保存下来。

实验分为两组:(1)在电机运行开始前，通过上位机设定电机的转速为22 (°)/s，记录电机从起动到稳定这一过程的电机位置信息和转速信息。(2)在电机运行开始前，先设定电机的转速为12 (°)/s，当电机运行稳定后再设定电机的转速为1.8 (°)/s，实现电机的调速控制，记录这整个过程电机的位置信息和转速信息。

实验结束后，将两组实验得到的电机位置信息导入到MATLAB，确定Q，R，P0以及X^0 的值进行初始化，按照图1 的递归流程实现卡尔曼滤波器，得到基于卡尔曼滤波的速度观测值，并把滤波后的速度值与系统测得的速度值进行比较，以验证卡尔曼滤波器的滤波及辨识转速的性能。

实验中使用的Q，R 参数如下:Q =60，R =8.762×10-3。

3 实验结果分析

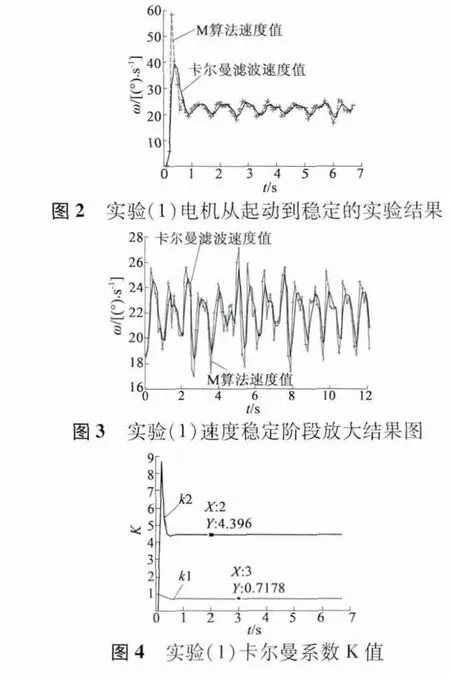
图2 ～图4 为实验(1)的实验结果:M 算法得到的曲线受噪声的影响跳动较大，尤其在电机的瞬时起动阶段有明显的过冲，电机定子的振动在起动阶段还并不稳定，存在电机振荡情况。并且实验室中采用光电编码器测量超声波电动机的转速信息时需要用到联轴器，由于实验台加工精度的影响，电机起动时联轴器的弹性环节使得测试结果中速度有较大的振荡。由图2 可以看出，卡尔曼滤波算法得到的速度曲线基本上贴近M 算法的结果，速度估算动态跟随性比较好，并且曲线变得更加的平滑，对电机起动阶段的速度超调有明显的抑制作用，最大超调从36 (°)/s 降低到17 (°)/s。在稳定阶段也可以看出较好的滤波性，图3 为图2 中稳定阶段的放大图，相较于M 算法，卡尔曼滤波后的转速值方差从3.87降低到2.18，波动由4.13 (°)/s 降低到2.85 (°)/s。

图5 ～图6 为实验(2)的实验结果，由图5 的实验结果可以看出，卡尔曼滤波算法在电机的调速过程中表现出较好的跟随性，但是在电机转速突变的过程中，卡尔曼滤波算法的误差增大并且存在一定的延时。而在稳定阶段还是表现出了良好的抑制噪声作用。在第一段速度阶段，转速的最大超调由14.2 (°)/s 减少到9.2 (°)/s，稳定阶段的波动也明显减小，由3 (°)/s 降低到2.2 (°)/s。在第二段低速阶段，稳定阶段的波动由0.7 (°)/s 降低到0.5(°)/s。整个调速过程(包括转速突变误差较大过程)转速值方差由28.45 降低到26.34。

卡尔曼滤波虽然解决了噪声的问题，但是由实验结果可以看出，这种方法在估测电机转速动态过程中还存在滞后性，尤其在转速突变时更加明显，在调速阶段，滞后最大达到0.3 s，这在以后的实验研究中还有待改进。

4 卡尔曼滤波的改进

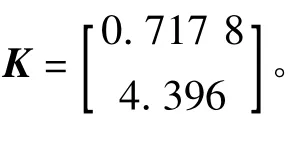
5 结 语

本文提出了一种基于卡尔曼滤波的超声波电动机测速算法，通过选取电机的位置信息作为观测变量对速度信息进行估计。仿真结果表明，该方法改善了M 测速算法存在的误差较大的问题，速度动态跟随性好，更加接近电机的真实速度。但是，该方法在调速的动态过程中还存在着一定的滞后性，对于高性能的控制要求还不能够满足要求。并且在初值的选取上还是主要依靠的试凑法，适应性还有待进一步的研究。

［1］ 陈振，刘向东，靳永强，等. 采用扩展卡尔曼滤波磁链观测器的永磁同步电机直接转矩控制［J］.中国电机工程学报，2008，28(33):75 -81.

［2］ 张猛，肖曦，李永东.基于扩展卡尔曼滤波器的永磁同步电机转速和磁链观测器［J］.中国电机工程学报，2007，27(36):36-40.

［3］ 林海，严卫生，李宏，等.基于无迹卡尔曼滤波的永磁同步电机无传感器直接转矩控制［J］.西北工业大学学报，2009，27(2):204 -208.

［4］ PRAESOMBOON S，ATHAPHAISAL S，YIMMAN S. Sensorless speed control of DC servo motor using Kalman filter［C］//Information，Communications and Signal Processing，ICICS 2009.IEEE，2009:1 -5.

［5］ ZHANG Wei，LUO Jianjun.Speed and rotor flux estimation of induction motors based on extended Kalman filter［C］//Networked Computing and Advanced Information Management (NCM).IEEE，2010:157 -160.

［6］ YIN Zhonggang，XIAO Lu，SUN Xiangdong.A speed and flux estimation method of induction motor using fuzzy extended Kalman filter［C］//Electronics and Application Conference and Exposition(PEAC).IEEE，2014:693 -698.

［7］ 王磊，李宏，武明珠.基于扩展卡尔曼滤波的永磁同步电机参数辨识［J］.微特电机，2012，40(7):19 -22.

［8］ 潘胜辉，郝东亚，张兴达. 基于扩展卡尔曼滤波的GPS 动态测速算法［J］.信息技术，2014，38(12):13 -16.

［9］ 何栋炜，彭侠夫，蒋学程，等.永磁同步电机的改进扩展卡尔曼滤波测速算法［J］.西安交通大学学报，2011，45(10):59 -63.

［10］ SHI Tingna，WANG Zheng，XIA Changliang.Speed measurement error suppression for PMSM control system using self - adaption Kalman observer［J］. IEEE Transactions on Industrail Elecrtonics，2014，62(5):2753 -2763.

［11］ ISHIGURO H，YAMAMOTO M，TSUJI S.Omni-directional Stereo［J］. IEEE Transaction on Pattern Analysis and Machine Intelligence，1992，14(2):257 -262.

［12］ 宋刚，秦月霞，张凯，等. 基于普通编码器的高精度测速方法［J］.上海交通大学学报，2002，36(8):1169 -1172.

［13］ 陈旻.基于DSP 的扩展卡尔曼滤波直流无刷电机控制［J］.单片机与嵌入式系统应用，2003，(11):63 -66.

［14］ 于红霞，胡静涛.基于自适应卡尔曼滤波的异步电机转速和负载转矩估计［J］.数据采集与处理，2012，27(5):552 -558.

［15］ 宋春迎. 动态定位中的卡尔曼滤波研究［D］. 长沙:中南大学，2006:21 -36.