基于二阶滑模观测器的永磁同步电动机无传感器控制

刘 江

(包头职业技术学院，包头014030)

0 引 言

为了更准确、方便地获得永磁同步电动机转子位置和速度，通常利用位置传感器进行检测，最常见的有编码器和旋转变压器，这种检测方法通常是电机控制系统设计较为常用的方案。但是这种机械传感器检测方法在一些特殊情况下并不能满足控制性能要求，例如当在温度、强烈机械振动情况下，这些机械传感器的性能将受到很大影响，导致检测精度降低，甚至不能正常工作。采用高精度、高响应传感器又势必增加控制系统的成本，此外这种传感器增加了电机系统的尺寸和体积，从而在一些空间有限的系统中不能正常使用。为了解决上述机械传感器弊端，国内外大量学者对此进行了研究，一些无位置传感器的控制策略得到广泛研究，例如高频信号注入法［1-3］、状态观测器［4-5］、磁链估计法［6-7］、滑模观测器［8-10］等。其中滑模观测器因其具有较强的鲁棒性、动态响应速度快，因而得到广泛关注。

但是滑模观测器自身存在抖振现象，从而影响了电机位置和转子速度观测精度。为了削弱抖振，通常在滑模观测器中加入低通滤波器和边界层法等控制方法。低通滤波器虽然能够有效削弱抖振，但会造成相位滞;而边界层法不能保证在边界范围内收敛到零。

本文针对永磁同步电动机无位置传感器控制实际需求，提出了一种新型二阶滑模观测器，并用Lyapunov 方法证明该观测器的稳定性。新型二阶滑模观测器相比于传统滑模观测器能够在没有滤波器的情况下有效削弱抖振现象，同时能够获得更加精确的转子位置和转速。最后通过仿真实验进一步验证该方法的有效性。

1 永磁同步电动机数学模型

建立如图1 所示的永磁同步电动机(以下简称PMSM)d-q 数学模型，在同步旋转坐标(d -q)下，PMSM 数学模型可以表示:

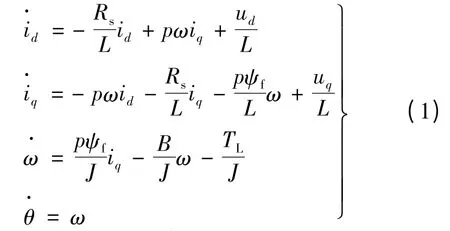
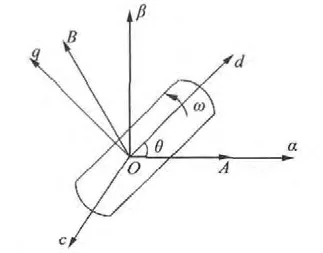
图1 永磁同步电动机d-q 坐标系

式中:id，iq和uq，ud分别为电机d 和q 轴电流和电压;Rs为定子电阻;L 为定子电感;ψf为电机的永磁通;J 为转动惯量;B 为粘性摩擦系数;ω 为角速度;θ为转子位置。

将式(1)变形可得:

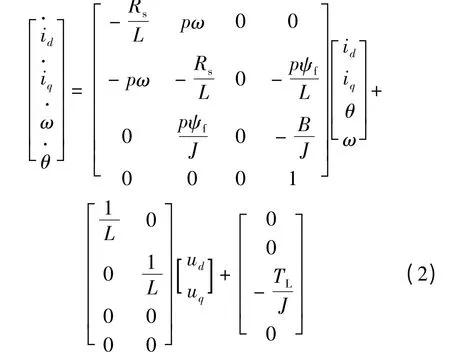
PMSM 位置和速度的估算均以反电动势为基础，因此将PMSM 在d-q 坐标系下的数学模型转换为α-β 静止坐标下的数学模型:

式中:iα，iβ分别是定子α，β 轴电流;uα，uβ分别是定子α，β 轴电压;eα，eβ分别是定子α，β 轴反电动势;其中:

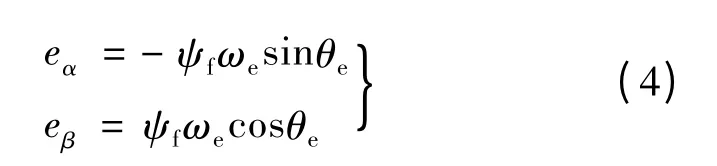
2 二阶滑模观测器设计

2.1 传统滑模观测器

根据PMSM 在静止坐标系下的数学模型式(3)设计的滑模观测器如图2 所示，表达式如下:

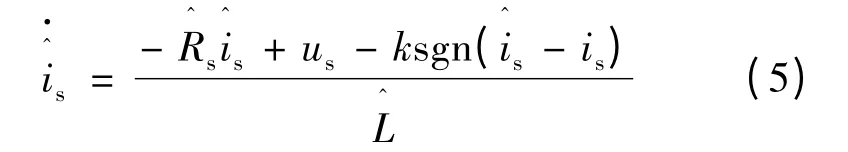
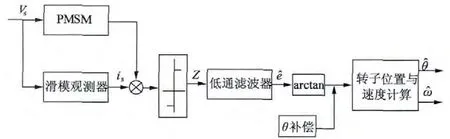
图2 滑模观测器框图

电机估算速度和位置:

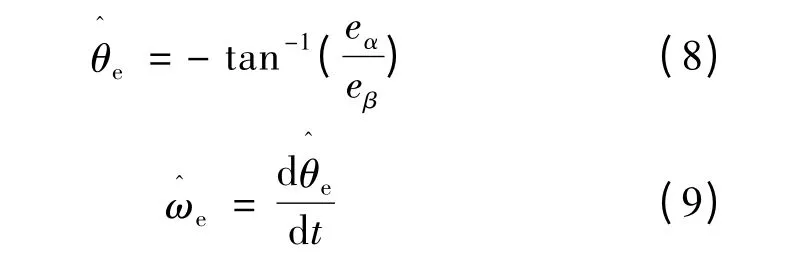
低通滤波器的加入导致了反电势幅值的减小，幅值随着电机转速的增大而增大，因此为了准确地对电机转速估算，需要进行补偿。低通滤波器采用形式如下:

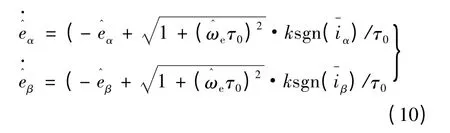
由式(4)可以算出电机转速和转子位置的估算值:

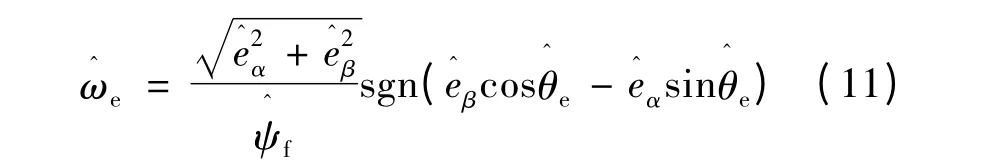
由于低通滤波器会使反电势相位滞后，因此对式(12)转角估算值进行有效补偿，补偿后的转角估算值:

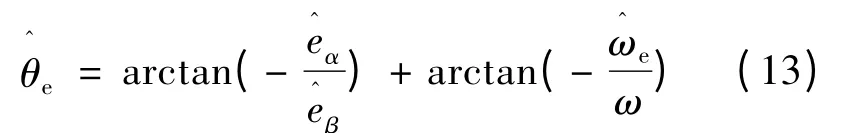
式中:ω=1/τ 为低通滤波器的截止频率。

2.2 新型二阶滑模观测器

为了避免传统滑模观测器抖振以及采用低通滤波器而导致的相位滞后问题，提出了一种新型二阶滑模观测器。该新型滑模观测器在不采用低通滤波器的情况下消除了滑模抖振现象，新型二阶滑模观测器系统框图如图3 所示。

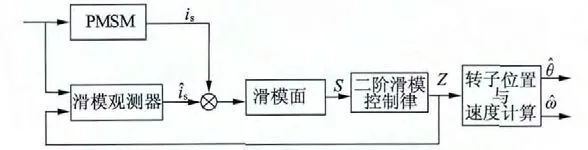
图3 新型二阶滑模观测器框图

新型滑模观测器设计:

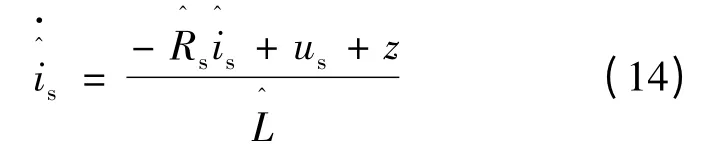
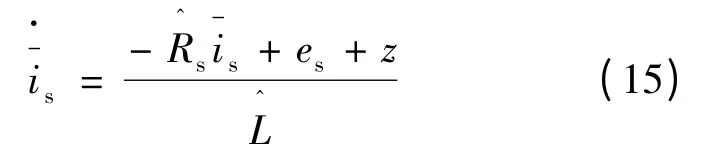
滑模面定义:

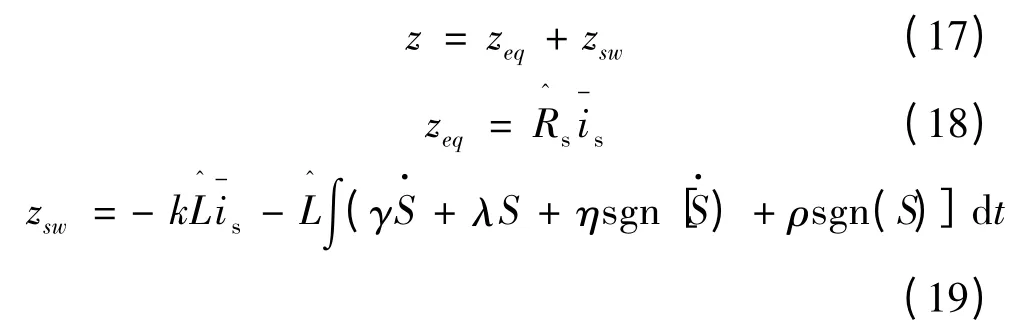
3 稳定性分析

设李雅普诺夫函数定义:

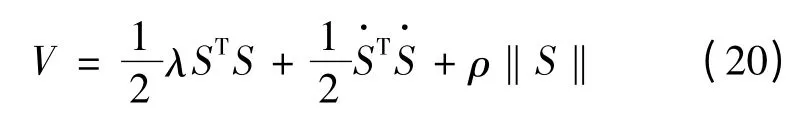
对式(20)求导可得:

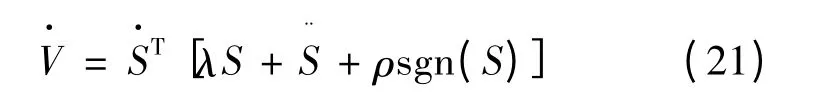
由式(16)可以将式(21)改写:

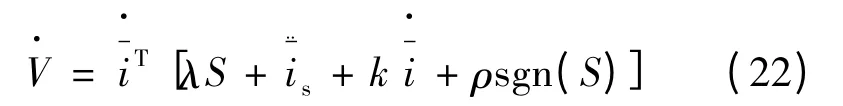
由式(15)、式(17)、式(18)、式(19)可得:

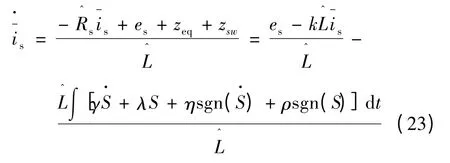
由此可得:

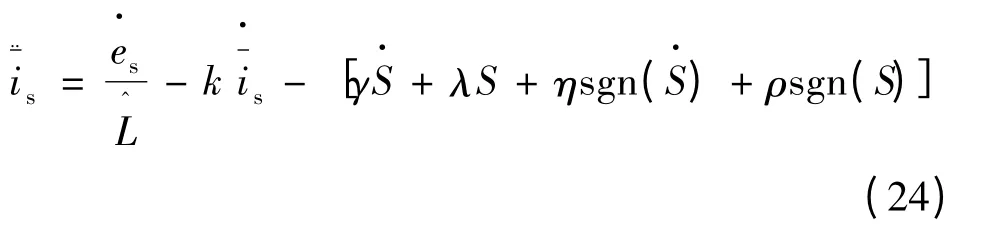
将式(24)代入到式(21)中可得:

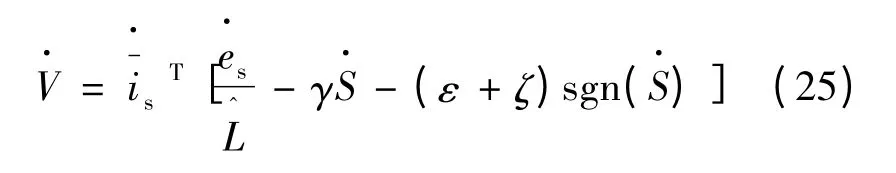
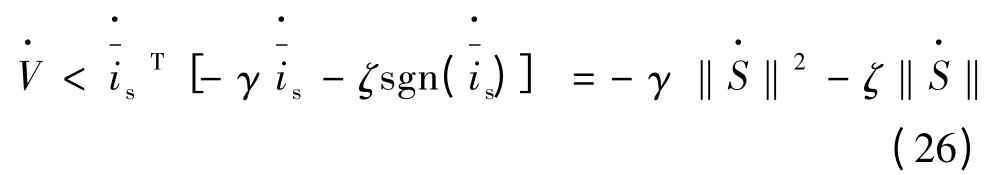
由以上分析可以看出，二阶滑模观测器能够保证电机定子电流误差很快收敛到零，并且由于控制信号z 的连续性，从而避免了滑模系统的抖振问题，进一步提高了系统的控制精度。

4 仿真实验

在MATLAB/Simulink 仿真环境下，对PMSM 无位置传感器控制系统进行了仿真实验，对电机采用传统滑模观测器和新型二阶滑模观测器控制时电机速度和转子位置进行跟踪估算，通过比较分析以验证本文所提到的二阶滑模观测器的有效性和可行性。电机和控制器的主要参数如表1、2 所示。

表1 PMSM 主要参数

表2 控制器主要参数

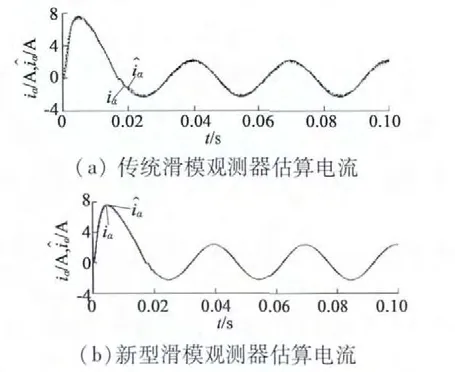
图4 传统滑模观测器和新型滑模观测器估算电流仿真

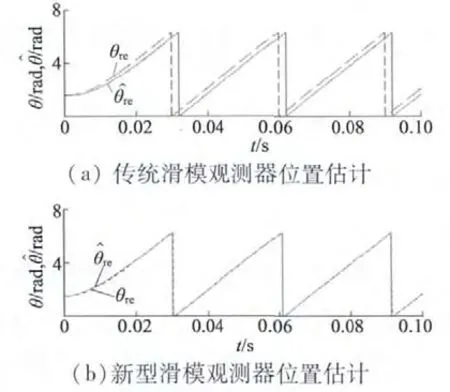
图5 传统滑模观测器和新型滑模观测器转子位置仿真

传统滑模观测器和新型二阶滑模观测器仿真对比结果如图4、图5、图6 所示，其中虚线代表实际值，实线代表观测值。由图4 ～图6 可以看出:(1)传统滑模观测器电流估计值存在明显的抖振现象，估计精度不高;而新型二阶滑模观测器能够有效削弱滑模固有抖振现象，估计电流也能以较快速度收敛;(2)传统滑模观测器估计转子位置存在滞后问题，存在一定误差;而新型二阶滑模观测器能够在不引入低通滤波器的情况下，较快地跟踪电机转子位置，误差较小;(3)新型二阶滑模观测器相比于传统滑模观测器转速估算值波动较小，提高了观测精度，稳定性较好。

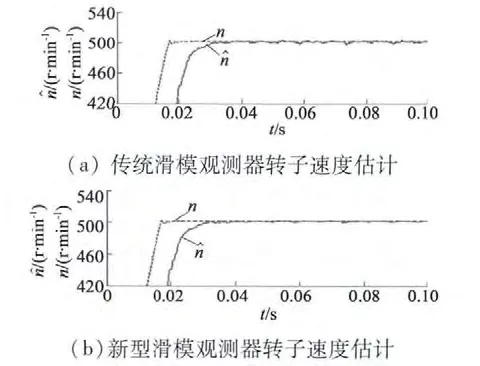
图6 传统滑模观测器和新型滑模观测器转子速度仿真

5 结 语

本文针对传统的滑模观测器存在抖振现象，在传统滑模观测器基础上提出了一种新型的二阶滑模观测器用来估计PMSM 的转子位置和速度。该新型滑模观测器在不引入低通滤波器的情况下有效避免了滑模系统抖振现象，最后采用李雅普诺夫稳定理论证明了所提出的二阶滑模观测器的稳定性。仿真试验表明，该新型滑模观测器相比于传统滑模观测器具有更高的观测精度，为PMSM 的无位置传感器检测提供了一种有效可行的方法。

［1］ 贾洪平，贺益康.基于高频注入法的永磁同步电动机转子初始位置检测研究［J］.中国电机工程学报，2007，27(15):15 -20.

［2］ JANG J H，SUL S K，HA J I，et al. Sensorless drive of surface -mounted permanent-magnet motor by high - frequency signal injection based on magnetic saliency［J］. IEEE Transactions on Industry Applications，2003，39(4):1031 -1039.

［3］ JANG J H，HA J I，OHTO M，et al.Analysis of permanent-magnet machine for sensorless control based on high-frequency signal injection［J］. IEEE Transactions on Industry Applications，2004，40(6):1595 -1604.

［4］ XU J F，WANG F Y，XIE S F，et al.A new control method for permanent magnet synchronous machines with observer［C］//Preceedings of the IEEE 35th Annual Power Electronics Specialists Conference，2004，2:1404 -1408.

［5］ GAUR P，AZIZ M，MITTAL A P，et al.Sensorless control schemes for permanent magnet synchronous motor ［C］//Preceedings of the IEEE Region 10 Conference on Computers，Communications，Control and Power Engineering，2005:1 -4.

［6］ FRENCH C，ACARNLEY P. Control of permanent magnet motor drives using a new positionestimation technique［J］.IEEE Transactions on Industry Applications.1996，32(5):1089 -1097.

［7］ 孙海军，郭庆鼎，高松巍，等.系统辨识法永磁同步电机无传感器控制［J］.电机与控制学报，2008，12(3):244 -247.

［8］ XU L Y，WANG C J. Implementation and experimental investigation of sensorless control schemes for pmsm in super-high variable speed operation［C］//Proceedings of the 1998 IEEE Industry Applications Conference，1998，1:483 -489.

［9］ YONG F，YU X H，MAN Z H. Non - singular terminal sliding mode control of rigidmanipulators ［J］. Automatica. 2002，38(12):2159 -2167.

［10］ 陈荣，邓智泉，严仰光.永磁同步伺服系统电流环的设计［J］.南京航空航天大学学报，2004，36(2):220 -225.