双绕组永磁容错电机优化设计
2015-03-12朱景伟曹林柏李小庆
王 霞,朱景伟,曹林柏,李小庆
(大连海事大学,大连116026)
0 引 言
近20 年来,永磁电机发展迅速,在国防军事、航空航天、交通运输等安全性要求较高领域的电力作动系统中得到了广泛应用[1]。随着电力作动系统的不断发展与完善,电力作动器采用具有高的功率密度、可靠性和容错能力的电机势在必行。现今,虽然电机性能已经达到了较高的水平,但其容错能力还有待提高。从根本上说,提高电机的容错性可能会增加电机成本,增大损耗,使得效率低于对应的普通结构电机,为解决这一问题,永磁容错电机及其驱动系统应运而生[2],经过十几年的发展,已成为高可靠性电机驱动系统的研究热点[3-4]。本文提出一种带相冗余的永磁容错电机结构,利用BP 神经网络提高了解析法计算电感精度,较传统从电机结构入手分析的方法更为简单有效。结合粒子群寻优算法和BP 神经网络高精度电感解析式,可以优化槽口设计和最小气隙,得到能有效抑制短路电流的电感。根据解析法和有限元法求解结果,在能够实现容错的结构基础上,优化永磁体形状,有效减小反电动势谐波和空载转矩脉动。
1 电感计算
根据课题要求确定电机的基本性能参数:额定功率PN=500 W,额定转速nN=3 000 r/min,额定转矩TN=1.59 N·m,额定直流供电电压Udc=100 V。约束条件包括:额定效率ηN≥80%,额定功率因数cosφN≥0.8,空载反电动势有效值约为54 V,谐波畸变率THD≤3%,齿槽转矩脉动Tcog≤5%TN,各相绕组之间的互感小于自感的5%,短路电流Ishort小于1.25 倍的额定电流IN,即对应的自感≥19 mH。根据电机设计的性能要求和约束条件,可以求得如表1 所示的电机参数,其绕组分布和基本结构如图1所示,相数m 为3,槽数Qs为12,极对数p 为4,A,B,C 相互差120°电角度,A 与A0,B 与B0,C 与C0同相,互为冗余。
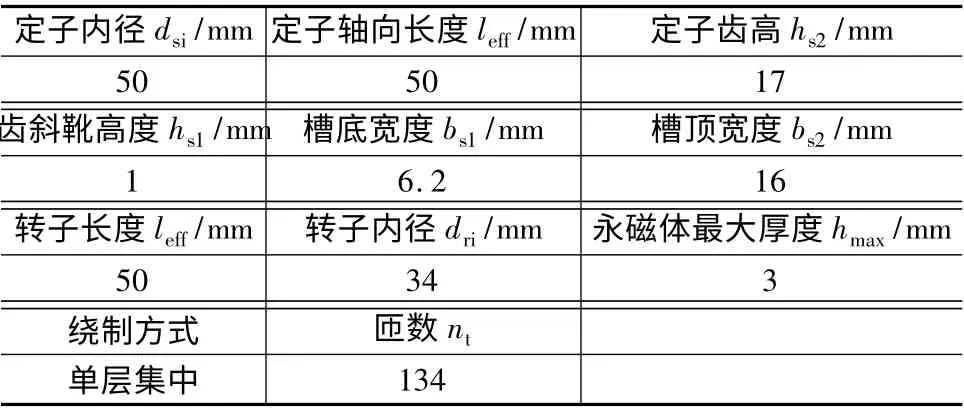
表1 电机参数表
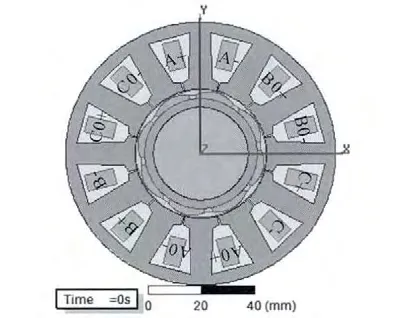
图1 双绕组3 相8 极永磁容错电机结构图
电机的优化设计内容包括抑制短路电流、降低空载反电动势谐波畸变率、减小空载反电动势。电机采用单层集中绕组,绕组之间具有较强的磁隔离能力,互感较小,可以通过优化槽口设计和最小气隙,提高自感以抑制短路电流,在电机出现开路、短路或组合故障时,仍能稳定运行[5]。
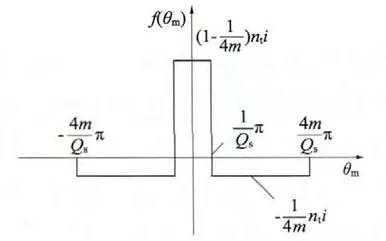
图2 磁动势在气隙中的分布图
单相绕组磁动势在气隙中的分布如图2 所示,i为瞬时电流,nt为匝数,θm为沿着定子圆周相对于定子齿中心线的角度,一相激磁绕组的磁动势f(θm)、气隙中心处的径向磁密b(θm)和总磁链Ψs分别:
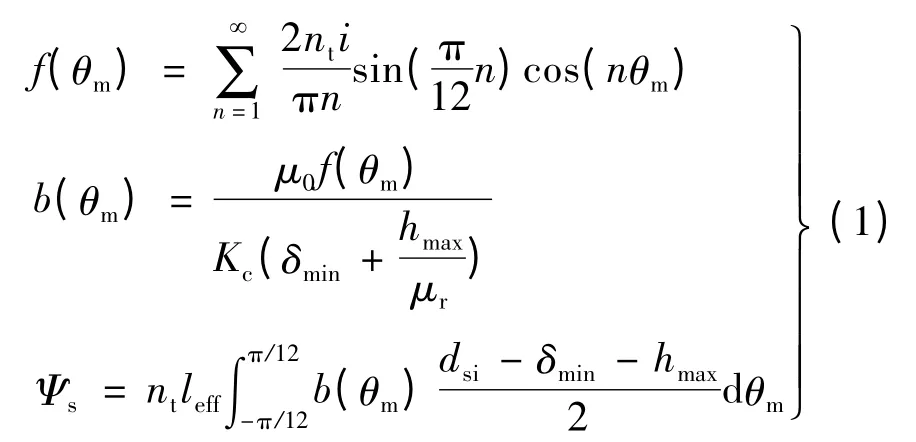
式中:Kc为卡特系数;hmax为永磁体最大厚度;δmin为最小气隙长度;dsi为定子内径;μ0为真空中的磁导率;μr为空气的相对磁导率;leff为定子有效长度,则绕组的总激磁感:
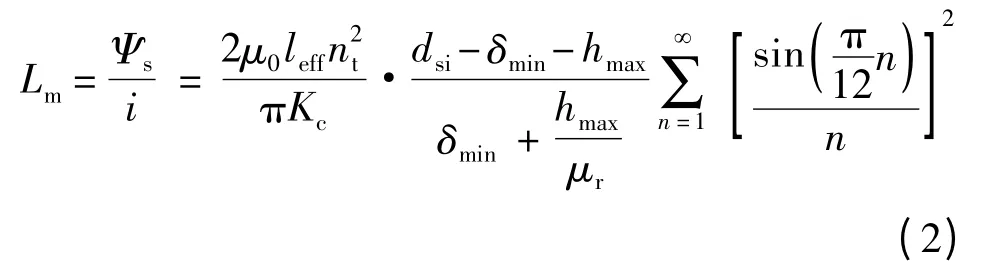
双绕组永磁容错电机采用图1 的槽口结构,考虑槽口边缘效应后的槽口漏感:
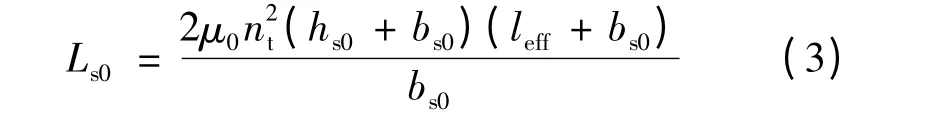
通过简化槽口结构可得槽内漏感:
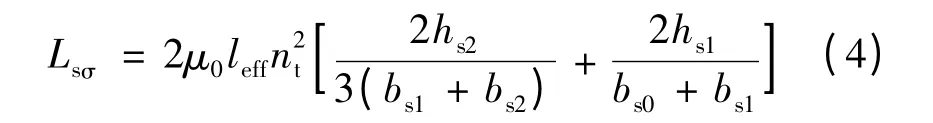
式中:bs0为槽口宽度;hs0为槽口厚度;bs1为槽底宽度;bs2为槽顶宽度;hs1为齿斜靴高度;hs2为定子齿高。
绕组的自感由总激磁感、槽口漏感和槽内漏感组成,表达式:
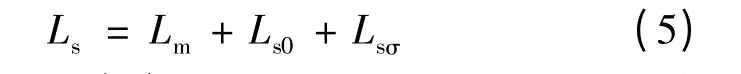
由式(2)~式(5)可知,在基本结构参数确定后,自感的主要影响量为δmin,bs0和hs0。利用解析法和Ansoft Maxwell 14 的有限元法计算,研究在δmin恒定时bs0和hs0联合变化对自感的影响,如图3(a)和图3(c)所示。自感随着δmin的增大而稍微减小,随着bs0的增大而减小,hs0的增大而增大,为了抑制短路电流,需要合理减小bs0,增大hs0,选择合适的δmin。两种方法计算的误差曲面如图3(b)和图3(d)所示,自感随参数变化的规律一致,最大误差小于6%,解析法可以用于分析参数变化时的电感变化规律,但解析法精度还不能满足电感优化设计的要求,需要结合有限元法,提高解析法的电感计算精度,以便于对槽口参数和最小气隙优化设计,增大电感以抑制短路电流,达到短路容错控制要求。
从电机结构入手,准确计算电感,需要建立新的高精度磁路等效模型,重新确定槽口漏感、槽内侧漏感、激磁电感的解析式,计算较为复杂。随着智能控制技术的不断深入,电机优化设计的建模方向开始转向神经网络智能建模。本文以槽口宽度bs0、槽口厚度hs0和最小气隙δmin为变量,利用电感解析,以有限元法计算值为目标,运用BP 神经网络,可得到电感Ls的高精度表达式[6-7]。
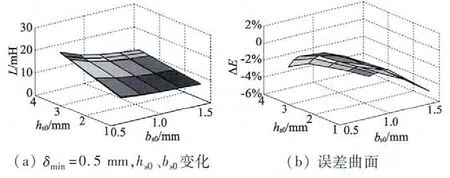
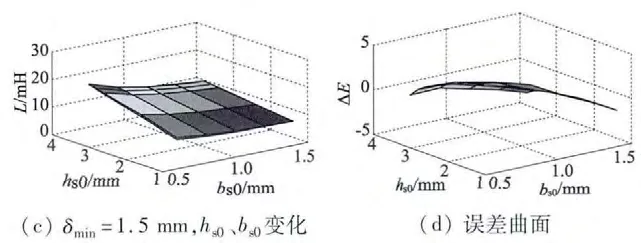
图3 利用解析法与有限元的电感及误差曲面图
利用MATLAB 中的randperm 函数重新排列样本,在打乱顺序的样本中随机选择40 个作为学习训练集,其余10 个样本作为测试集,通过试验,选择神经网络数为13,学习率为0.001,根据给定的δmin,hs0,bs0算出解析法对应的自感,利用BP 神经网络,训练得到解析法计算自感与有限元计算自感之间的关系,然后根据神经网络结构,确定其函数关系。BP 神经网络的训练和测试结果如图4(a)、图4(c)所示,误差如图4(b)、图4(d)所示,最大误差不超过0.6%,满足电感优化设计要求,在得到电感精确解析式后,可以利用粒子群寻优算法确定槽口参数。
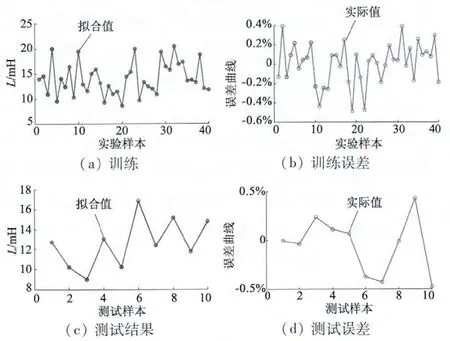
图4 训练结果
根据粒子群寻优(PSO)算法原理,在MATLAB中编程实现基于PSO 的槽口及最小气隙参数寻优,适应度函数为BP 神经网络计算电感值与根据电机短路电流和反电动势计算的设计目标电感值之差的平方[8]。设目标电感为20 mH,以适应度函数的最小值为目标,最优个体适应度值变化如图5 所示。最终得到最优个体的适应度值为0,粒子位置:bs0=0.600 0 mm,hs0=3.206 8 mm,δmin=0.500 0 mm,对应BP 神经网络计算电感为20 mH。
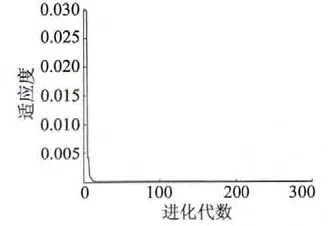
图5 最优个体适应度值
2 反电动势及齿槽转矩脉动优化
采用单层集中绕组和深而窄的槽口结构,不利于减小反电动势谐波和齿槽转矩脉动,需要通过求解其解析式分析影响因素来进行优化设计。电枢绕组的磁通:
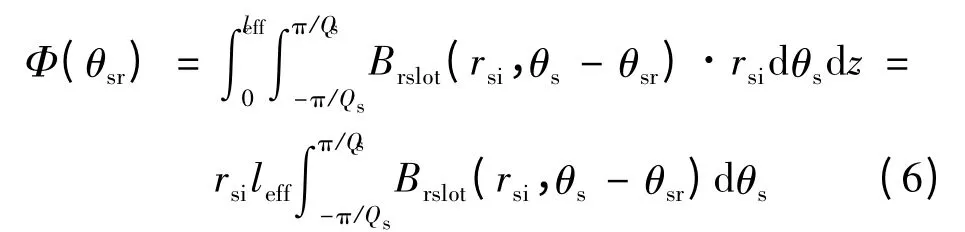
式中:rsi为电机定子内半径;θsr指相绕组轴线距离永磁体中心线的空间位置角;θs指距离相绕组中心线的空间位置角;Brslot为考虑定子开槽时的气隙磁密径向分量。根据法拉第电磁感应定律可得定子绕组的反电动势:
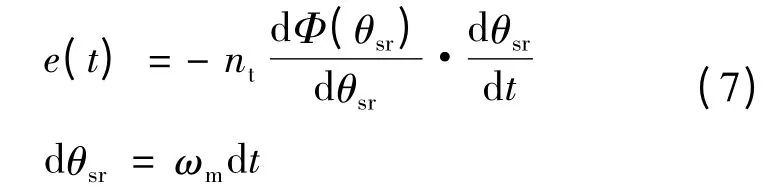
式中:ωm为机械角速度。对于永磁电机,储存在磁场中的能量:
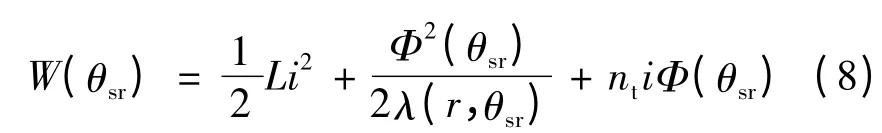
式中:L 为定子绕组自感;i 为定子绕组相电流;λ(r,θs)为气隙磁导函数。空载时,i =0,由磁共能产生的空载转矩脉动表达式:
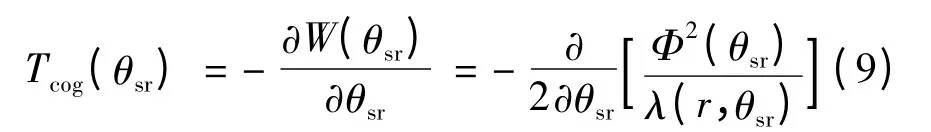
由式(7)~式(9)可知,优化电机的反电动势和齿槽转矩,关键在于对考虑定子开槽时气隙磁通密度径向分量的优化。永磁体外表面与转子圆心的距离:
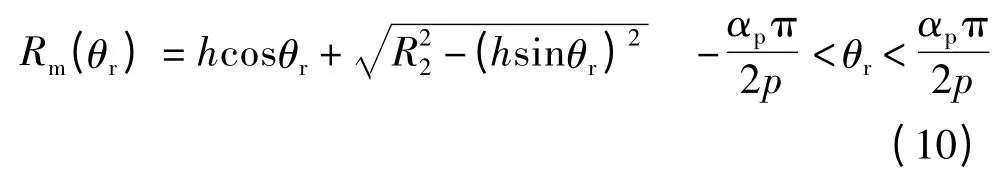
式中:h 为离心高度;θr为距离永磁体中心线的空间位置角;R2为永磁体半径;αp为极弧系数,假设铁心材料磁导率无穷大,永磁体退磁曲线为直线,且采用平行充磁,利用磁场基本关系、范定方程和边值条件可计算出不考虑定子开槽气隙磁感应强度径向分量Br1:
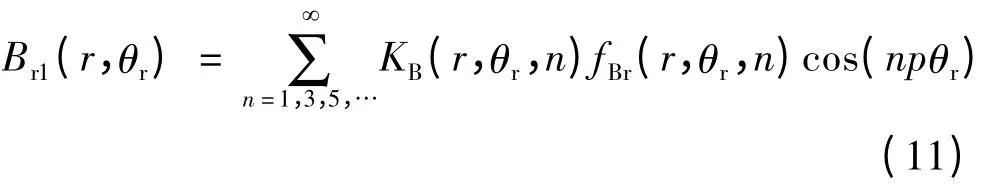
式中:
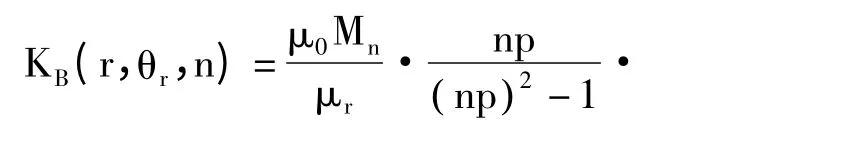
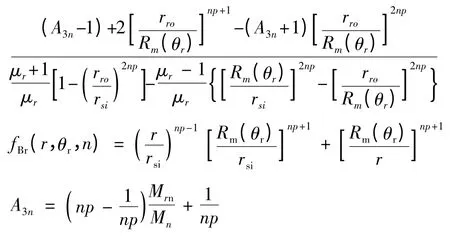
式中:rro为不计永磁体时的转子外径;r 为气隙中心处半径;Mrn,Mθn,Mn分别对应于傅立叶分解中径向、切向和总磁化强度n次谐波分量系数,Mn=Mrn+npMθn。槽口的引入也会影响气隙磁场分布,考虑定子开槽时的气隙磁密[9-11]:
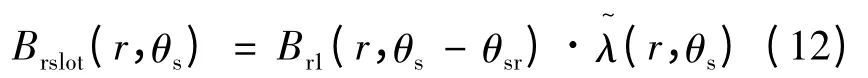
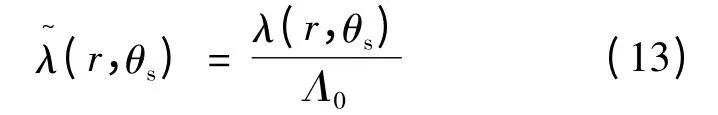
式中:Λ0为μ0/g1,g1为有效气隙长度。将磁感应强度解析式应用于双绕组三相容错电机中,由于有限元法导出的数据是离散的,为使得数据定义域一致,将解析法所得结果与有限元法对应。由图6 可知径向磁密的解析法计算结果与有限元法基本一致,具有较高的精度,便于电机优化设计。
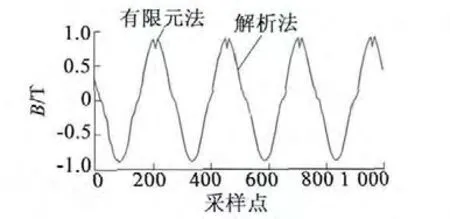
图6 计及槽口时的气隙磁密径向分量波形图
由解析式可知,基本结构、槽口和最小气隙等参数确定后,径向磁密主要与永磁体形状有关。永磁体形状成为影响齿槽转矩脉动和反电动势谐波含量的主要因素,直接从解析式分析,计算困难,而且不直观,采用有限元法,在Ansoft Maxwell 2D 中可直接得到空载反电动势和齿槽转矩脉动的波形,利用其内置函数可得空载反电动势的有效值和谐波畸变率,以及转矩脉动峰值,求解方便。
空载反电动势的幅值(E0)及其谐波畸变率(THD)和齿槽转矩脉动峰值(Tcog)在电机基本参数确定以后,主要取决于转子磁钢的离心设计与极弧系数的配合。利用Ansoft Maxwell 2D 仿真,取离心高度h 为0,5 mm,10 mm,11 mm,12 mm,13 mm,14 mm,15 mm,16 mm,极弧系数αp为0. 55,0. 60,0.65,0.70,0.75,0.80,0.85,0.90,0.95,得到空载转矩脉动峰值、空载反电动势的有效值和谐波畸变率随离心高度h 和极弧系数αp的变化的三维曲面图如图7、图8、图9 所示。
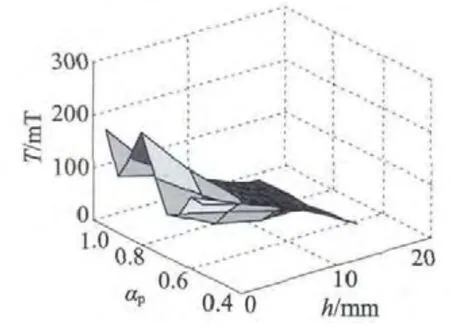
图7 空载齿槽转矩脉动
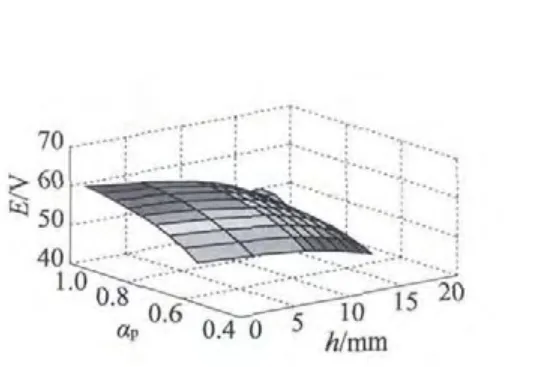
图8 空载反电动势有效值
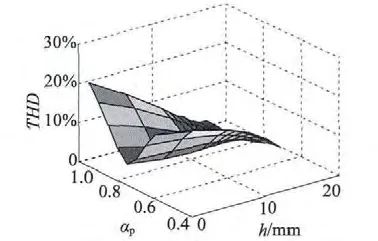
图9 空载反电动势谐波畸变率
由7 可得,空载转矩脉动峰值随着离心高度的增加而减小,随着极弧系数的增加变化比较复杂,在αp=0.75 附近可取得齿槽转矩脉动峰值最小的设计。仅从空载转矩脉动峰值和加工可能性考虑,在取αp=0.80,h=15 mm 时最优。由图8 和9 可得,随着αp的增大,反电动势有效值增加,谐波含量先减小后增大,但随着h 的增加,反电动势的有效值和谐波含量减小,说明引入离心高度,可以有效减小谐波有效值。选择合适的αp和h 配合,既可以获得较大的电动势幅值提高转矩输出能力,又能有效减少谐波分量。减小谐波分量可以从THD 观察,在极弧系数αp=0.8 附近都能取得空载反电动势THD 最优的设计。由以上图表可得,在离心高度h ≥13 mm,极弧系数αp在0.75 ~0.85 之间时,能兼顾齿槽转矩脉动和反电动势谐波,获得比较好的设计。采用离心磁钢设计,永磁体在中心处的气隙较小,而在极尖处的气隙较大,气隙磁通密度接近正弦波,可有效减小反电动势谐波含量、降低齿槽转矩脉动,提高电机寿命。
3 结 语
本文在得到三相八极双绕组永磁容错电机电感解析表达式的基础上,利用BP 神经网络提高了电感计算精度,使得有限元法和解析法的计算误差小于0.6%,满足电感优化设计要求。采用粒子群寻优算法,利用所得高精度电感解析式,得到优化后的槽口宽度、槽口厚度、最小气隙长度。在得到气隙磁密径向分量解析式的基础上可求得反电动势、空载转矩脉动的解析式,分析影响因子后,结合有限元法,对永磁体形状进行优化设计,得到离心高度和极弧系数分别在13 ~15mm和0.75 ~0.85之间,可以有效减小反电动势谐波含量,抑制空载转矩脉动。本文所述电机电感、反电动势、齿槽转矩脉动的优化方法也适用于多相永磁容错电机。
[1] 王秀和.永磁电机[M].北京:中国电力出版社[M].2007:252-279.
[2] 刘震,林辉,司利云. 开关磁阻发电系统的故障分析及仿真[J].电力系统及其自动化学报,2005,17(5):7 -11.
[3] MECROW B C,JACK A G. Design and testing of a four - phase fault-tolerant permanent magnet machine for an engine fuel pump[J].IEEE Transaction on Energy Conversion,2004,19(2):132 -137.
[4] SUN Z G,WANG J B,GERAINT W J,et al. Enhanced optimal torque control of fault-tolerant PM machine under flux weakening operation[C]//Proceedings of International Conference on Electrical Machines,2008:1403 -1408.
[5] 郝振洋,胡育文,黄文新,等.电力作动器中永磁容错电机的电感和谐波分析[J].航空学报,2009,30(6):1063 -1069.
[6] CHANG P R,YANG W H.Environment-adaptation mobile radio propagation prediction using radial basis function neural networks[J].Vehicular Technology,1997,46(1):155 -160.
[7] ZHANG C Q,QI R N,QIU Z W. Comparing BP and RBF neural network for forecasting the resident consumer level by MATLAB[C]//ICCEE 2008,International Conference on Computer and Electrical Engineering,2008:169 -172.
[8] 史峰,王辉,郁磊,等.MATLAB 智能算法30 个案例分析[M].北京:北京航空航天出版社,2011.
[9] ZHU Z Q,HOWE D,BOLTE E.Instantaneous magneticfield distribution in brushless permanent magnet DC motors:Part III:Effect of stator slotting[J].IEEE Transactions on Magnetics,1993,29(1):152 -157.
[10] ZHU Z Q,HOWE D.Improved analytical model of predicting the magnetic field distribution in brushless permanent magnet[J].IEEE Transactions on Magnetics,2002,38(1):229 -238.
[11] WANG X,LI Q,Wang S.Analytical calculation of air-gap magnetic field distribution and instantaneous characteristics of brush-less dcmotors[J]. IEEE Transactions on Energy Conversion,2003,18(3):424 -432.
