小学生数字线估计中的分段策略

邢 强，徐争鸣，蔡新华

（广州大学 教育学院 心理学系，广东 广州 510006）

小学生数字线估计中的分段策略

邢 强，徐争鸣，蔡新华

（广州大学 教育学院 心理学系，广东 广州 510006）

摘要：采用3[数字线估计任务类型：0-100 (15 cm)、0-100 (10 cm)、0-1 000(15 cm)]×3(年级：二、四、六)的混合实验设计，探讨小学生数字线估计的发展特点及分段策略的作用.结果发现：（1）随着年级的增长，小学生的数字线估计准确性不断提升.（2）数字线估计任务中，表征模式发展趋势为：二年级主要采用对数函数，四、六年级主要采用线性函数.（3）二、四年级学生使用分半策略，六年级学生使用偶分策略.

关键词：小学生；数字线估计；表征模式；分段策略

1　问题提出

数字线估计作为一种重要的数学认知能力，是以内部近似准确的量化标准为依据对实际的线段进行的操作，儿童在数字线估计上的表现是其对“数”精确加工程度的体现[1]，数字线估计是数估计研究中常用的研究范式.所谓数估计就是由一种数量表征转换为另一种数量表征的过程中，只要有一种表征形式涉及到数字的估计便可称为数估计[2].数字线估计是一种纯数估计，控制了数字单位和生活经验等额外变量，有很高的生态效度，具体做法是让被试估计一个数在一条线段上的位置，即要求被试把数字表征转化为以长度来表征的数量.当前对数字线估计的研究取得了大量成果[3~6]，形成了对数规则模型、存储器模型、线性规则模型、重叠波理论等一系列理论模型[7].前3种模型都把数字线估计的内部表征模式视为单一的策略或运算模式，即对数表征（指数字估计的估计值与估计数量呈对数函数图象）、等级可变性表征（是指数字估计的协方差即估计值的标准化差除以被估计的数字是恒定的这一现象）和线性表征（是指数字任务中按照线性函数来表征所要估计的数字），这些策略或模式不会随文化教育、情境等因素的改变而改变.但不同模型所采用的不同精确度的表征模式引起人们对数估计心理表征发展的思考，促使重叠波理论的产生.重叠波理论认为，儿童的数估计会从不精确的对数表征发展到精确的线性表征，且变化是突然的、整体性的.出现这种变化的原因是随着年级的增长，会不断积累数字线估计的表征经验，在获得表征的适当性信息前，个体会重复常用的表征，随着经验的增加，选择不常用表征的可能性越来越大.当人们通过反馈获得了有关精确表征的经验后，个体会突然放弃常用的对数表征，选择不常用的线性表征.例如：在对0-100数字线估计任务中，幼儿园的孩子遵循对数模式，二年级学生遵循线性模式[8~10].在0-1 000数字线的估计任务中，二年级学生的估计遵循对数模式，四年级学生中一半的人遵循对数模式，一半的人遵循线性模式，大多数六年级的学生采用线性表征[11]，但是另一项研究显示在0-1 000范围内大部分四年级学生掌握了线性表征[7].

同时，已有研究认为表征是一种策略或者估计模式，可以通过积累数字线估计的经验，获取对表征适当性进行反馈的信息以强化线性表征并消退对数表征，或在更加熟悉的数标尺中进行估计以提高估计精确度[2].年级和经验增长能解释数字线估计精确性的提高和表征模式的发展，而儿童在数字线估计过程中采用的策略能进一步解释年级和经验是如何促进数字线估计发展的[11].国外已有研究证实儿童及成人最常使用的策略是将数字线分段[12~13]，分段策略是指在数字线估计前根据特殊比例将数字线分段.被试会内隐地按特殊分段点划分数字线，把特殊分段点作为参照点来引导估计，数字离最近的参照点越远，估计变异性越大.按照不同的特殊比例，可把分段策略分为奇分策略和偶分策略，奇分是指根据1/N（N为奇数）分段；偶分策略是指根据1/N（N为偶数）分段，如果是根据中点分段的话就叫做分半策略，它是一种特殊的偶分策略，即在选取参照点时首先会采用中点[4].研究主要探讨偶分策略，因为人们更习惯把线段分为偶数段，使线段在分段后仍然有对称性.

小学儿童在数估计任务中，由对数表征模式突然地完全转变到线性表征模式，从而显著提升了数估计成绩，这到底是由年级的增长、知识经验的增加所造成的，还是因为在表征过程中儿童使用了不同的策略，又或者这两个原因都导致了重叠波理论中的表征转换呢？首先，研究者试图探讨不同年级数估计表征模式的发展性特点；其次，试图通过比较分半点、偶分点和其它点的估计准确性探讨分段策略中的分半策略和偶分策略是否能提高数估计的准确性.数字线估计能力的发展体现为表征转换，那么它是怎么发生的呢？研究者将从纵向上考察这个表征模式的变化，同时从横向上比较儿童在不同数范围下是否会选择不同的表征模式.因此，研究选取了二、四、六年级的学生为被试，以探讨清楚在0-100 和0-1 000数范围的数字线估计任务上表征模式的发展特点.

综上所述，研究的基本假设是：

H1：随着年级的增长，儿童的数估计表征会从对数表征转向线性表征，数字线估计的准确性也不断提高；

H2：数字线长度和数范围的变化会影响小学生数字线估计的精确性和估计模式；

H3：数字线估计中的分段策略表现为从分半策略向偶分策略的过渡，是数字线估计中的常用策略，但存在年级差异.

2　研究方法

2.1被 试

二、四、六年级小学生共360人，每个年级分别为114、88和158人，其中男生185人，女生175人.

2.2设 计

两因素混合设计，组间变量是年级，分为：二、四、六年级；组内变量是任务类型，有3种：15 cm长0-100数标尺的数字线，即0-100(15 cm)、10 cm长0-100数标尺的数字线，即0-100(10 cm)、15 cm长0-1 000数标尺的数字线，即0-1 000(15 cm).

2.3材 料

材料做成了3个小册子，每个册子有11页纸，分别呈现3种类型的任务：0-100(15 cm)、0-100(10 cm)和0-1 000(15 cm).每一页中间有一条标出端点数的线段，在线段中间上方2.5 cm处标数字，0-100数范围内呈现的数字有7、13、19、25、43、50、61、75、83、88、和97；0-1 000数范围内呈现的数字有70、130、190、250、430、500、610、750、830、880、和970.这些数字均随机呈现.

第一种任务采用了莫雷、周广东和温红博（2010）研究中的材料，线段长度为15 cm，端点为“0”和“100”；第二种任务中的线段改变了其长度，变为10 cm，端点为“0”和“100”；第三种任务中的线段则改变了它的数范围，变为0-1 000，线段长度为15 cm，端点为“0”和“1 000”.改变数字线长度和数范围一方面是为了检验数字线长度和数范围是否影响数字线估计任务的难度进而影响估计精确性和估计模式，另一方面是为了检验同一年级的儿童在不同类型数字线上是否会选择不同的表征模式.这3种数字线上被估计的点所对应的位置在数字线上的比例都为7%、13%、19%、25%、43%、50%、61%、75%、83%、88%和97%，其中13%接近1/8，25%为1/4，50%为1/2，75%为3/4，88%接近7/8，选择这些分段比例以探讨数字线估计中的偶分策略.

2.4程 序

主试为经过培训的心理系研究生.首先主试给全班同学发小册子，然后按照指导语引导进行集体施测，指导语如下：“同学们：我们今天做一个‘猜数字在哪里’的小游戏.在这个小本子上，每一页上都有一条线段，线段的左端点表示‘0’，右端点表示‘100’或‘1 000’，它们之间有很多数字，但没把这些数字标在线段上，现在就请你猜一猜线段上方的数字在线段上的哪个地方，你认为数字在哪里，就请你在线段上的这个地方画一条竖线.请不要用直尺或三角板量.”

施测过程中保持教室安静，不给予被试任何反馈.实验持续20分钟，结束后回收所有题册.

2.5计分与数据处理

估计结果由主试以直尺测量，精确到毫米，然后转换为估计值.

数估计成绩的指标为绝对误差百分比（percent absolute error，简称PAE），其计算公式为：PAE=|估计值－实际值|÷被估计的数值范围×100%.采用统计分析软件SPSS18.0进行统计处理.

3　结果与分析

3.1小学儿童数字线估计的准确性

儿童在数字线估计任务中的估计成绩的PAE反映了其数估计的精确性.表1描述了二、四、六年级在0-100(15 cm)、0-100(10 cm)、0-1000(15 cm)这3种数字线估计任务中的估计PAE.

表1　二四六年级儿童在3种数字线估计任务中PAE的描述统计

为了了解儿童数字线估计准确性的发展情况，分别对在0-100(15 cm)、0-100(10 cm)、0-1 000(15 cm)这3种数字线估计任务中，二、四和六年级估计的PAE进行了单因素方差分析，结果发现，在0~100(15 cm)数字线估计任务中，二、四和六年级之间估计的PA E差异显著，F (2 , 3 960)=127.47，p<0.001；在0-1 000(15 cm)数字线估计任务中，二、四年级和六年级之间估计的PAE差异显著，F(2, 3 960)=87.88，p<0.001；在0-100(10 cm)数字线估计任务中，二、四和六之间估计的PAE差异显著，F(2, 3 960)=125.98，p<0.001.进一步事后检验（LSD）发现，在0-100(15 cm)、0-100(10 cm)、0-1 000(15 cm)这3种数字线估计任务中，二年级的PAE显著高于四和六年级的PAE，四年级的PAE显著高于六年级的PAE.

分别比较二、四和六年级在0-100(15 cm)和0-100(10 cm)数字线估计任务中的PAE，考察数字线长度的变化对儿童数字线估计精确性的影响.通过独立样本T检验发现，二年级在0-100(15 cm)和0-100(10 cm)数字线估计任务中的PAE无显著差异，t(1 253)=0.10，p>0.05.四年级在0-100(15 cm)和0-100(10 cm)数字线估计任务中的PAE无显著差异，t(967)=-1.77，p>0.05.六年级在0-100(15 cm)和0-100(10 cm)数字线估计任务中的PAE无显著差异，t(1 737)=-1.10，p>0.05.

分别比较二、四和六年级在0-100(15 cm)和0-1 000(15 cm)数字线估计任务中的PAE，考察数字线范围的变化对儿童数字线估计精确性的影响.通过独立样本T检验发现，二年级在0-100(15 cm)数字线估计任务中的PAE显著低于在0-1 000(15 cm)数字线估计任务中的PAE，t(1 253)=-11.00, p<0.001.四年级在0-100(15 cm)数字线估计任务中的PAE显著低于在0-1 000(15 cm)数字线估计任务中的PAE，t(967)=-8.02，p<0.001.六年级在0-100(15 cm)数字线估计任务中的PAE显著低于在0-1 000(15 cm)数字线估计任务中的PAE，t(1 737)=-8.11，p<0.001.

3.2小学儿童数字线估计的表征模式

以实际呈现的数值为自变量，以儿童估计值的中位数作为因变量（选中位数而不是平均数作为因变量是为了排除极值的影响），曲线估计检验了各个年级对3种类型数字线估计的中位数对线性、对数函数的拟合度（分别表示为LinR2和Log R2），结果见表2.

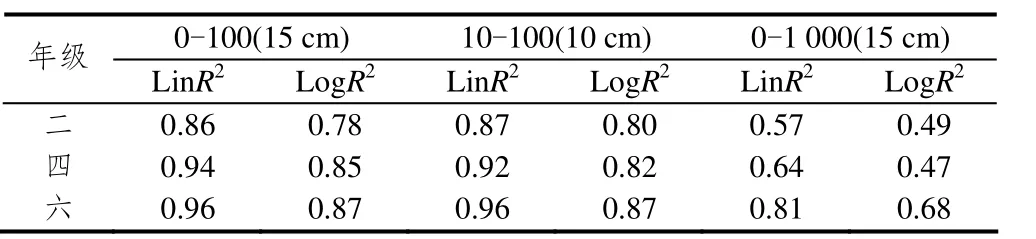
表2　不同年级儿童3种类型数字线下估计中位数拟合度分析

由表2可知，3个年级儿童数字线估计的中位数对这两种函数的拟合度都很高，回归方程也都有显著性.在0-100(15 cm)、0-100(10 cm)、0-1 000(15 cm)3种数字线任务中，各个年级儿童估计的中位数对线性函数比对对数函数的拟合度都更高.

为了验证拟合度差异的显著性，对两模型预测值的绝对误差进行了配对样本T检验，比较了以下两个量的差异：对数函数对二、四、六年级学生在0-100(15 cm)、0-100(10 cm)、0-1 000(15 cm) 3种数字线任务中实际呈现数与估计值中位数关系的拟合度（二、四、六年级学生在3种数字线任务中估计值中位数与对数函数对实际呈现数预测值之差），线性函数对二、四、六年级学生在0-100(15 cm)、0-100(10 cm)、0-1 000(15 cm) 3种数字线任务中实际呈现数与估计值中位数关系的拟合度（二、四、六年级学生在三种数字线任务中估计值中位数与线性函数对实际呈现数预测值之差）.结果见表3.

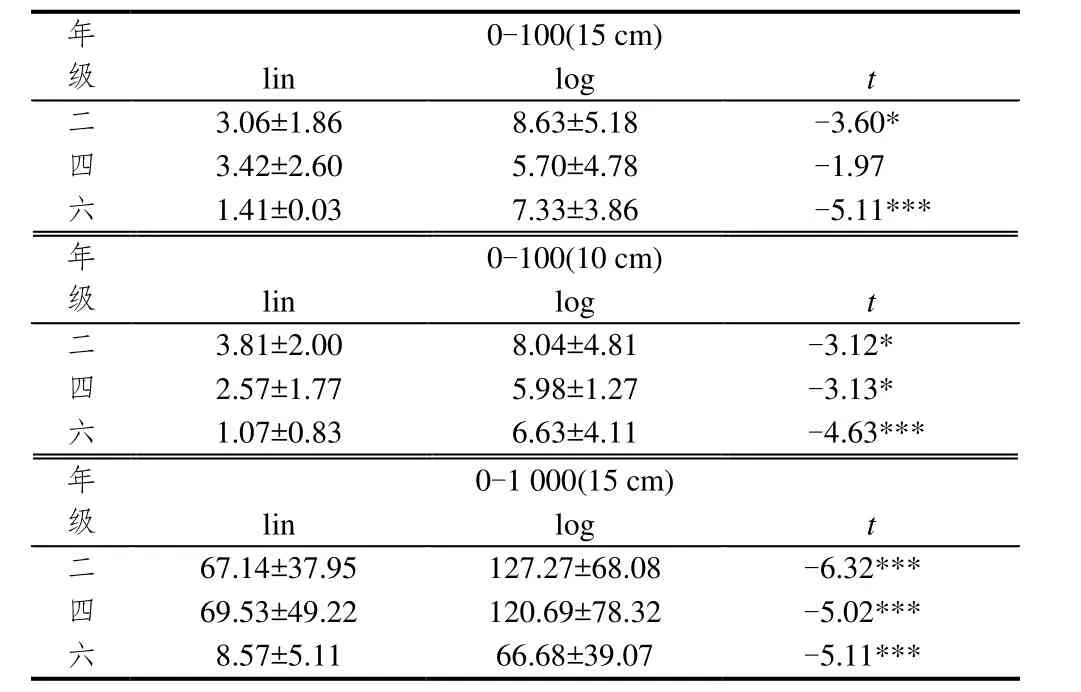
表3　对数和线性函数对3个年级在3种任务中实际呈现数与估计值中位数关系的拟合度的差异分析

由表3可知，二年级在0-100(15 cm)、0-100(10 cm)、0-1 000(15 cm)这3种数字线任务中，对数函数与线性函数对实际呈现数与估计值中位数拟合度的差异均显著（t(10)=3.60，p<0.05；t(10)=-3.12，p<0.05；t(10)=-6.32，p<0.001），说明二年级在所有的数字线估计任务中采用了线性表征.

四年级在0-100(10 cm)、0-1 000(15 cm)这两种数字线任务中，对数函数与线性函数对实际呈现数与估计值中位数拟合度的差异均显著（t(10)=-3.13，p<0.05；t(10)=-5.02，p<0.001），说明四年级在0-100(10 cm)、0-1 000(15 cm)这两种数字线任务上采用了线性表征.

六年级在0-100(15 cm)、0-100(10 cm)、0-1 000(15 cm) 这3种数字线任务中，对数函数与线性函数对实际呈现数与估计值中位数拟合度的差异（t(10)=-5.11，p<0.001；t(10)=-4.63，p=0.001；t(10)=-5.11，p<0.001）.说明六年级在所有的数字线估计任务中采用了线性表征.

3.3不同年级对3种类型数字线上不同点估计准确性比较3.3.1 0-100(15 cm)数字线上估计不同点的准确性

表4描述了在0-100(15 cm)数字线估计任务中，二、四、六年级估计7、13、19、25、43，50、61、75、83、88和97这11个点的PAE，采用方差分析，发现：二、四、六年级估计不同点的PAE均有显著差异（F(10, 1 244)=10.95，p<0.001；F(10, 958)=25.86，p<0.001；F(10, 1 728)=16.64，p<0.001）.

进一步事后检验（LSD）发现，二年级学生估计50（分半点）的PAE显著高于估计13、19、25、43、75的PAE （ps<0.05），而估计7、61、83和88这几个点的PAE无显著差异.四年级学生估计50的PAE显著低于估计13、19、25、43、61、75、83、88和97这9个数的PAE（ps<0.05）；六年级学生估计50的PAE显著低于估计13、19、25、43、61、75、83和88这8个数的PAE（ps<0.05），而与估计7和97的PAE无显著差异.

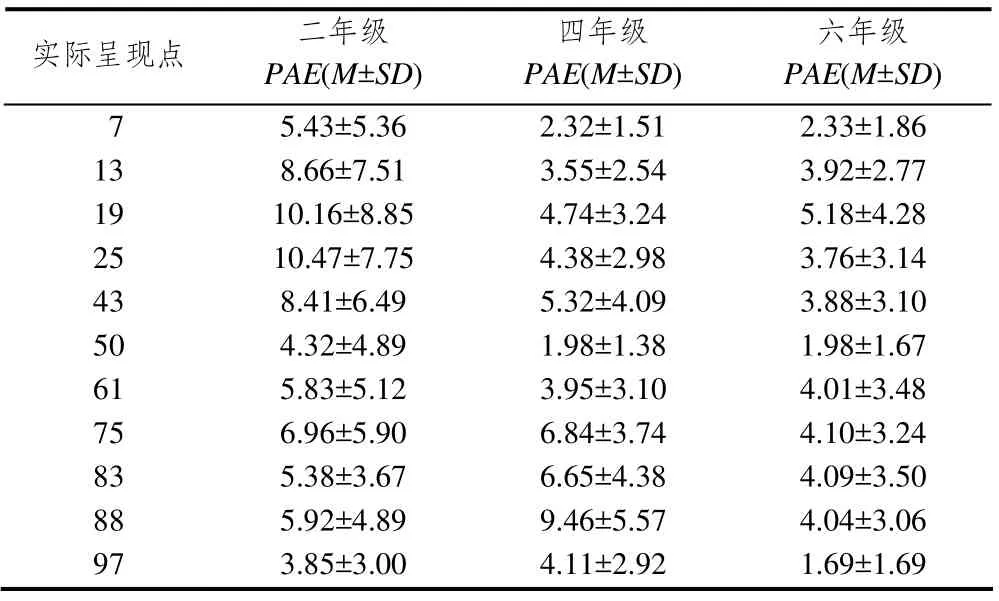
表4　不同年级估计0-100(15 cm)数字线上不同点的PAE

根据1/N（N为偶数）分段，得出偶分点有13、25、75、88，估计偶分点的PAE和估计其它数字的PAE进行比较发现，二年级学生估计88的PAE要显著低于估计19、43的PAE（ps<0.05），估计75的PAE显著低于估计19、25的PAE （ps<0.05），估计13、25的PAE显著低于估计7、61、83的PAE（ps<0.05）.四年级估计25的PAE显著低于估计83的PAE（p<0.05），估计75、88的PAE显著高于估计19、43、61、97的PAE（ps<0.05）.六年级估计88的PAE显著低于估计83的PAE（p<0.05）.

3.3.2 0-100(10 cm)数字线上估计不同点的准确性

表5描述了在0-100(10 cm)数字线估计任务中，二、四、六年级对7，13，19，25，43，50，61，75，83，88和97这几个点的估计准确性均有显著差异（F(10, 1 244)=10.62，p<0.001; F(10, 958)=18.1，p<0.001；F(10, 1 728)=12.71，p<0.001）.

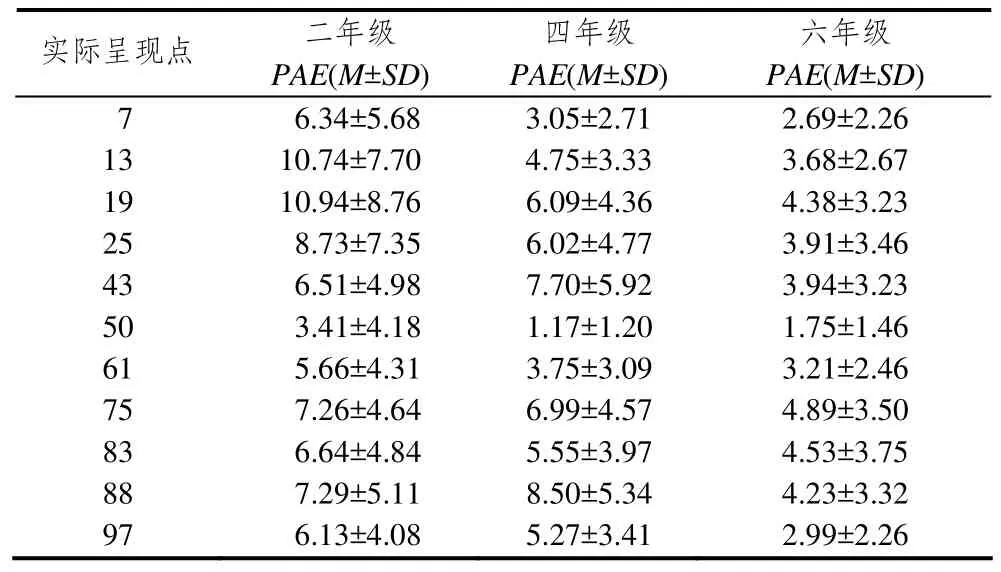
表5　不同年级估计0-100(10 cm)数字线上不同点的PAE

进一步事后检验（LSD）发现，3个年级的学生估计50（分半点）的PAE显著低于估计其它数的PAE（ps<0.05），说明他们在估计这条数字线时均准确掌握了分半策略.

根据1/N（N为偶数）分段，得出偶分点有13，25，75，88，估计偶分点的PAE和估计其它数字的PAE进行比较发现，二年级中，估计13的PAE显著高于估计7、43、61、97的PAE（ps<0.05）；估计25的PAE显著高于估计7、43、61和83的PAE（ps<0.05）；估计25的PAE显著高于估计43的PAE（p<0.05），四年级估计75、88的PAE显著高于估计61的PAE（ps<0.05）；六年级估计25、75、88的PAE显著高于估计97的PAE（ps<0.05）；估计13的PAE显著低于估计19的PAE（p<0.05）；估计25的PAE显著低于估计19的PAE（p<0.05）.

3.3.3 0-1 000(15 cm)数字线上估计不同点的准确性

表6描述了在0-1 000(15 cm)数字线估计任务中，二、四、六年级对7，13，19，25，43，50，61，75，83，88 和97这几个点估计的PAE均有显著差异（F(10, 1 244)=29.14，p<0.001；F(10, 958)=82，p<0.001，F(10, 1 728)=40.21，p<0.001）.

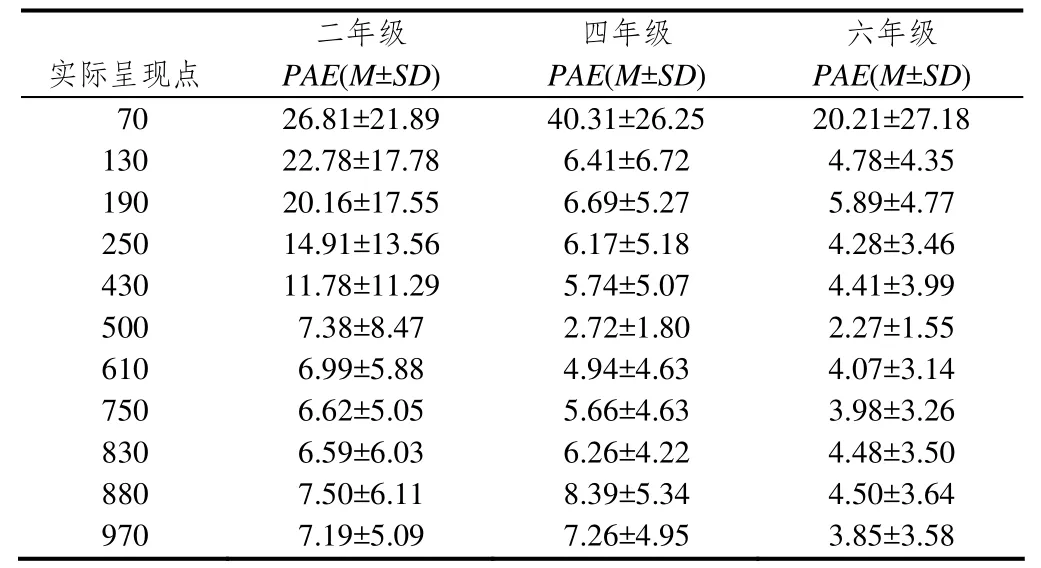
表6　不同年级估计0-1 000（15 cm）数字线上不同点的PAE

进一步事后检验（LSD）发现，二年级估计500的PAE显著低于估计70，130，190，250，430的PAE（ps<0.05），估计500的PAE与估计610、750、830、880、970的PAE无显著差异；四年级估计500的PAE显著低于估计其他数的PAE（ps<0.05）；六年级估计500的PAE显著低于估计70，130，190，830和880的PAE（ps<0.05），虽然估计其他数与估计500的PAE无显著差异，但PAE都很低.

根据1/N（N为偶数）分段，得出偶分点有130，250，750，880，估计偶分点的PAE和估计其他数字的PAE进行比较发现，二年级估计750、880的PAE显著低于估计70、190、430的PAE（ps<0.05），估计130的PAE显著高于估计610、830、970的PAE（ps<0.05）.四年级估计各个偶分点的PAE与估计其他数字的PAE无显著差异.六年级估计750的PAE显著低于估计190、430、830的PAE（ps<0.05）；估计250的PAE显著低于估计190的PAE（ps<0.05）.

4　讨 论

4.1小学儿童数字线估计准确性

对二、四、六年级数字线估计任务的PAE的分析表明：随着年级的增长，小学生的数字线估计准确性不断提升，说明教育会提升儿童数字线估计的准确性.例如：Siegler和Ramani也曾通过玩线性棋类游戏的方法提升了儿童数字线估计的成绩[14].

通过分别对二年级、四年级和六年级在0-100(15 cm) 和0-100(10 cm)数字线估计任务中的PAE比较发现，二、四和六年级在0-100(15 cm)数字线估计任务中的PAE与在0-100(10 cm)数字线估计任务中的PAE无显著差异.而莫雷等（2010）的研究发现一年级儿童在0-100(10 cm)数字线估计中的PAE低于他们在0-100(20 cm)数字线估计任务中的PAE，即随着数字线长度增长，估计的PAE降低.与莫雷等人研究的结果[15]相对比，不能判断数字线长度对数字线估计准确性有何影响，因此，还需再控制一些额外变量（如“数字线长度的变化幅度”）的基础上，进一步研究该问题.尽管数字线估计不受长度单位的影响，仍不能得出数字线估计精确性与测量知识无关的结论.通过分别对二、四和六年级在0-100(15 cm)和0-1 000(15 cm)数字线估计任务中的PAE进行比较发现，二、四和六年级在0-100(15 cm)数字线估计任务中的PAE显著低于在0-1 000(15 cm)数字线估计任务中的PAE，说明数字线估计任务数范围的扩展提升了任务难度，降低了数字线估计的精确性.只有当儿童掌握了0-1 000范围内的数知识，才能在0-1 000数范围数字线估计任务中有较高准确性.

4.2小学儿童数字线估计的表征模式

分别对二、四、六年级在0-100(15 cm)、0-100(10 cm)、0-1 000(15 cm)数字线估计任务中的数据进行分析，把每种类型估计值的中位数视为因变量，做实际呈现数的对数函数和线性函数的拟合（作群体估计模式的拟合），把单个被试的估计值视为因变量作实际呈现数的对数函数和线性函数的拟合（作个体估计模式的拟合）.通过比较对群体估计模式的拟合结果与对个体估计模式的拟合结果，发现一个不一致之处：对群体估计模式的拟合，四年级在0-100(15 cm)数字线估计任务中，与线性函数而非对数函数有较优拟合，但对数拟合与线性拟合的差异不显著.二、六年级估计0-100(15 cm)数字线任务时，线性函数的拟合度显著优于对数函数的拟合度.因此，在0-100(15 cm)数字线估计任务中，数字线估计的心理表征模式在年级间没有出现对数函数向线性函数的转变.对个体估计模式的拟合，在0-100(15 cm)数字线估计任务中，二年级更符合线性函数的人数比显著低于四、六年级，说明数字线估计的心理表征模式从二年级主要采用对数函数转向四、六年级主要采用线性函数.出现这种不一致的原因是：做群体估计模式的拟合是对实际呈现数与估计值的中位数的函数关系作对数函数或线性函数的拟合，做个体估计模式的拟合是对实际呈现数与单个被试估计值的函数关系进行拟合，当取众多单个被试估计值的中位数来概括多个被试的估计值时，会出现一些误差，比如说：估计值没有分析一些极端值.

因此，对个体估计模式的拟合结果比对群体估计模式的拟合结果更能解释儿童数字线估计的表征模式.对个体估计模式的拟合结果表明：在0-100(15 cm)数字线估计任务中，出现了从二年级主要采用对数表征转向四、六年级主要采用线性表征的变化情况，体现了表征模式的发展趋势，验证了重叠波理论的观点，即不同年级的孩子都拥有多重数估计心理表征.并且随着年龄和经验的增长，从主要采用不精确的对数表征，变得越来越多地采用精确的线性表征.

4.3小学生数字线估计中的分段策略

研究发现二、四、六年级估计0-100(10 cm)、0-1 000(15 cm)时均采用的是线性表征，那么在这两个任务中不同点估计错误百分比的差异不是因为采用了不精确的对数表征，有可能是受到分段策略的影响.如果估计分半点的错误百分比显著低于估计其它数的错误百分比，那么儿童采用了分半策略，在0-100范围的数字线估计任务中，分半点为50，在0-1 000范围的数字线估计任务中，分半点为500.如果在0-100范围的数字线估计任务中，估计13、25、75、88的错误百分比显著低于估计7、19、43、61、83、97的错误百分比，在0-1 000范围的数字线估计任务中，估计130、250、750、880的错误百分比性显著低于估计70、190、430、610、830、970的准确性，那么儿童采用了偶分策略，在数字线1/N（N为偶数）处进行分段.

通过对二、四、六年级学生在估计0-100(15 cm)、0-100(10 cm)、0-1 000(15 cm)数字线估计任务中不同点估计错误百分比的差异分别进行分析，发现二、四、六年级在三条数字线上均采用了分半策略.并且，二、四年级学生没有采用偶分策略，六年级学生采用了偶分策略.

研究证实低年级儿童已经掌握了分半策略：采用分半策略的四年级儿童人数比例与采用分半策略的六年级人数比例都很高，因为中点是线段上与两端距离相等的点，根据中点分段就很容易，只需要判断该点的左端和右端是否大致相等即可，儿童可以通过将绳子对折来模拟将线段分半，在他们判断出线段中点之前，他们会对中点两端数字线长度不断做出调整.尽管分半策略可以提供分半点与线段两端距离相等的信息，但Barth & Paladino发现[4]，进行数字线估计时，把中点作为参照点的儿童的估计成绩与没有采用中点为参照点的儿童的估计成绩无显著差异，主要原因是她们选用了平均年龄为5岁和7岁的被试，年幼儿童不能把整体量和部分量很好地联系起来，即使这个部分量是整体量的一半.

认为偶分策略的使用情况存在年龄差异的原因是五年级下学期开始学习因数和倍数、分数等与比例有关的数学知识，而六年级上学期进一步深化了分数的学习，并接触了百分数.所以六年级学生估计某些偶分点的PAE与估计某些非偶分点的PAE的差异不显著.因为分段通常不是为了把数字线分解为单位长度来转换标准单位，而是在估计前先在心里将估计物分解为较小的连续量，再用其它策略进行估计.比如他们常把分段策略与重组策略配合使用：将较小部分的估计相加或相乘.

5　结 论

随着年级的增长，小学生的数字线估计准确性不断提升；数字线估计任务中，表征模式发展趋势为：从不精确的对数模型向精确线性模型的过渡；数字线估计中的分段策略表现为从分半策略向偶分策略的过渡.

［参 考 文 献］

[1]徐华，陈英和.儿童数字线估计研究的述评与前瞻[J].心理研究，2012，（5）：46-50.

[2]Siegler R S, Booth J L. Development of Numerical Estimation in Young Children [J]. Child Development, 2004, 75(2): 428-444.

[3]徐群飞.中美学生估算能力研究[J].数学教育学报，2012，21（1）：73-75.

[4]Barth H C, Paladino A M. The Development of Numerical Estimation: Evidence Against a Representational Shift [J]. Developmental Science, 2011, 14(1): 125-135.

[5]陈丽兰.9~12岁儿童估算策略选择的发展特点[J].数学教育学报，2012，21（1）：48-51.

[6]刘国芳，辛自强.数字线估计研究：“模型”背后的策略[J].心理研究，2012，（5）：27-33.

[7]Siegler R S. Emerging Minds: the Process of Change in Children’s Thinking [M]. New York: Oxford University Press，1996.

[8]Opfer J E, Siegler R S. Representational Change and Children’s Numerical Estimation [J]. Cognitive Psychology, 2007，55(38): 169-195.

[9]Geary D C, Hoard M K, Byrd-Craven J, et al.Cognitive Mechanisms Underlying Achievement Deficits in Children with Mathematical Learning Disability [J]. Child Development, 2007, 78(4): 1 343-1 359.

[10]Geary D C, Hoard M K, Nugent L, et al. Development of Number Line Representations in Children with Mathematical Learning Disability [J]. Developmental Neuropsychology, 2008, 33(1): 277-299.

[11]Siegler R S, Opfer J E. The Development of Numerical Estimation: Evidence for Multiple Representations of Numerical Quantity [J]. Psychological Science, 2003, 14(3): 237-243.

[12]邢强，徐争鸣，蔡新华.数字线估计表征研究评述[J].广州大学学报，2012，（5）：48-51.

[13]陈丽兰.儿童估算策略选择研究述评及展望[J].数学教育学报，2009，18（3）：83-86.

[14]Siegler R S, Ramani B R. Playing Linear Numerical Board Games Promotes Low-Income Children’s Numerical Development [J]. Psychological Science, 2008, 11(5): 655-661.

[15]莫雷，周广东，温红博.儿童数字估计中的心理长度[J].心理学报，2010，（5）：569-580.

[责任编校：周学智]

Partitioning Strategy in Pupils Number Line Estimation

XING Qiang, XU Zheng-ming, CAI Xin-hua
(Department of Psychology, Guangzhou University, Guangdong Guangzhou 510006, China)

Abstract:A 3[(task: 0-100(15cm), 0-100(10cm), 0-1000(15cm)]cross 3 (grade: two, four, six) mixed design was used to investigate the mental representation of pupils and the efficiency of partitioning strategy in number line estimation. The results showed that: (1) The correlation between age and performance is high; (2) In number line estimation task, students of grade two rely on less accurate logarithmic number representations, students of grade four and grade six rely on more accurate linear representations with age; (3) Students of grade two and grade four use central partitioning strategy, and students of grade six apply even partitioning strategy.

Key words:pupils; number line estimation; representation pattern; partitioning strategy

作者简介：邢强（1973—），男，甘肃会宁人，教授，博士，主要从事认知与学习研究.

基金项目：教育部人文社会科学“十一五”规划项目——小学生数学问题表征特点与表征能力培养研究（09YJA880023）

收稿日期：2015-03-06

中图分类号：G420

文献标识码：A

文章编号：1004-9894（2015）04-0082-06