500 kV输电线路故障时空特性分析
2015-03-11罗杰蒋铁铮梁勇超马瑞
罗杰,蒋铁铮,梁勇超,马瑞
(1.长沙理工大学电气与信息工程学院,长沙市 410076;2.湖南省电力公司检修公司,长沙市 410002)
500 kV输电线路故障时空特性分析
罗杰1,2,蒋铁铮1,梁勇超2,马瑞1
(1.长沙理工大学电气与信息工程学院,长沙市 410076;2.湖南省电力公司检修公司,长沙市 410002)
随着电力系统通信自动化技术的发展,各种信息采集系统得到广泛应用,这为分析电网故障的时空特性提供了有利条件。以H省电网500 kV输电网为例,探讨了5年间500 kV输电线路故障在较长时间段上的行为特性。首先在输电线路故障时间序列层面上,统计分析输电线路故障发生的时间(单位:天)与同一时间点故障累计频次和累计概率之间的相互关系,采用Kolmogorov-Smirnov(K-S)法检验其分布的正态性,并根据R/S时序分析法计算出H省电网500 kV输电网5年间输电线路故障基于时序的Hurst指数,从而判断其在时间序列上具有长程相关性。然后,在空间层面上,统计分析5年期间H省电网每条500 kV输电线路故障次数与其发生频次和累计概率的关系,得出输电线路故障在空间上符合幂律分布特征。研究电网故障的时空分布特性为电网的风险管理和风险预测提供了辅助决策的依据。
输电线路故障;时空分布;幂律分布;Hurst指数;R/S分析法
0 引 言
现代社会在经济、生活等各方面都高度依赖安全、可靠供电,电力系统不仅是现代社会关键的基础设施,更是直接关系到国计民生的工业系统。随着国民经济的飞速发展,全社会对电能的需求不断增长,电网规模也随之不断扩大,电网已经发展成为大规模跨区的互联性复杂电网。一方面,不仅提高了电能传输的可靠性,降低了电能生产运营成本,另一方面,随着电网规模的扩大和复杂程度的提升,也增加了电网发生大面积停电的风险。这是因为电力系统属于非线性的动态系统,即使局部小范围的故障也可能给整个电网造成极恶劣的影响,从而产生重大的社会影响和经济损失[1-4]。
经典可靠性理论指出电网的线路故障可认为是近似服从泊松分布的独立事件,而单位时间内因故障跳闸的线路条数近似具有指数分布特征。也就是说,如果某次大规模停电与之相关跳闸线路的条数成一定的比例,那么该次大停电事故的规模也服从指数分布[5-6]。而通过大量实际电网大停电事故的统计分析表明,全球各国大停电的规模并不服从经典可靠性理论中所假设的指数分布,而是近似服从幂律分布[7-10],这是因为幂律分布呈现出明显的尖峰厚尾特性,这正印证了大规模停电事故由小事故引发,扩散区域大的实际情形,从另一方面也说明大规模停电事故的扩散概率大大超过预期。因为电力系统的复杂性和电网的动态特性,不仅使电力系统具有与生俱来的自组织临界性,而且从其故障规模上来说也具有长程相关性[11-12]。电力系统受负荷不断增长、外界扰动等因素的影响,都会使电力系统逐渐逼近自组织临界状态。而在这种状态下,若受扰动线路发生跳闸,系统的潮流将重新分布,这时就有可能造成系统其他线路连锁过负荷,使继电保护系统隐性故障爆发,从而使故障区域扩大,形成大停电事故的幂律特性[13-14]。虽然文献[15-16]分别通过对输、配电网故障的分析研究,表明电网故障和大停电事故一样,在时间序列上存在类似幂律分布特性以及故障的长程自相关性,但都未分析故障在空间上的分布特性和非线性关系。研究电网故障在空间上的分布特性能反映出电网中的薄弱环节。
在此背景下,本文以H省500 kV输电网为例,收集H省2008年—2012年期间500 kV输电线路故障数据,统计分析其时间尺度和空间尺度上的行为特征。首先统计输电线路日故障次数与其累计概率之间的关系,用Kolmogorov-Smirnov(K-S)方法检验其正态性,再采用Hurst指数理论计算输电线路故障时序的Hurst指数,判断其长程相关性和自相似性。最后,统计每条500 kV输电线路的故障次数与其发生频次和累计概率的关系,并检验线路故障在空间上的分布特性。
1 输电线路故障的时序统计分析及检验
1.1 数据来源及其统计分布特征分析
本文收集了2008年—2012年期间H省500 kV输电网47条输电线路的故障数据,分别记录了包括停电日期时间、停电线路名称、故障情况及原因和重合闸是否成功。整理5年1 826天数据,过滤出有效输电线路故障数据153条,并将所有故障数据按1年365天进行非线性统计分析,时间序列趋势如图1所示。
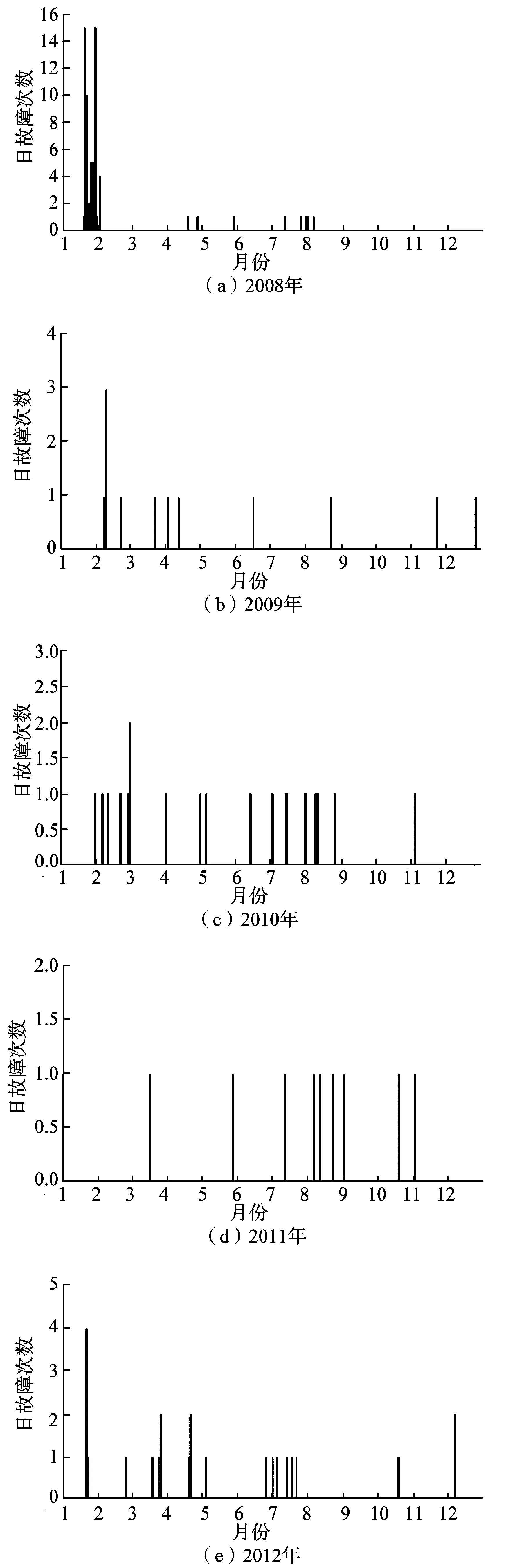
图1 H省500 kV输电线路日故障时序图Fig.1 Time series diagram of daily fault of 500 kV transmission line in H province
图1中横坐标为线路故障发生的时间(单位:天),纵坐标为某一天内故障累计发生的次数。由图1(a)可知,H省500 kV输电网因受2008年冰灾影响,在当年冬季500 kV输电网故障量猛增,1月中旬至2月初为500 kV线路跳闸高峰期,相比受恶劣灾害天气影响的2008年,2009年至2012年期间,虽然500 kV输电线路故障跳闸大多仍集中在冬季,但同比2008年,事故跳闸次数明显下降。从总体上看,H省500 kV输电线路故障并非表现出线性特征,而是呈现出非线性特征。为此需要对输电线路故障数据进行非线性统计分析。
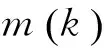
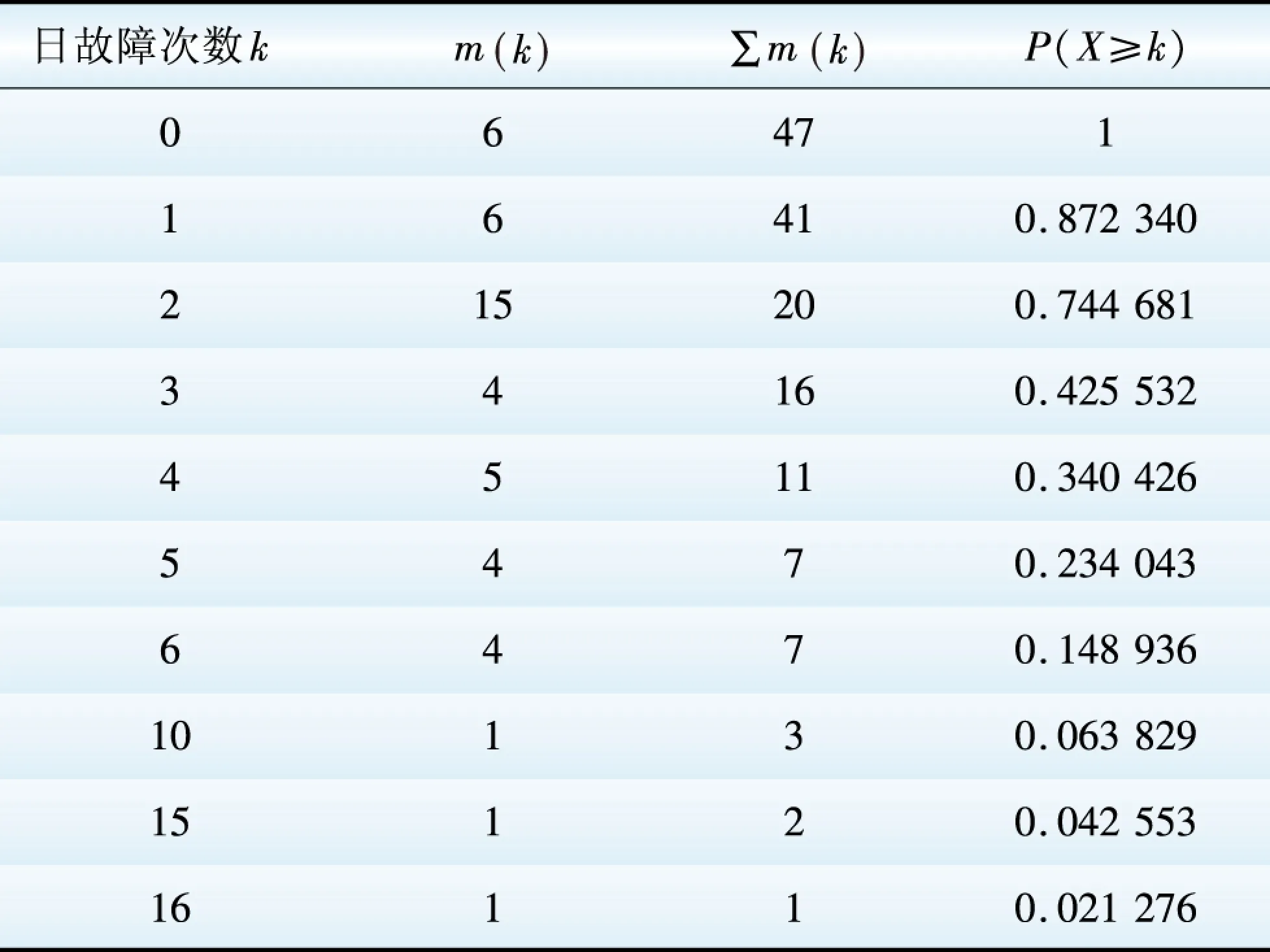
表1 日故障次数的统计数据
Table 1 Statistics of fault times in a day
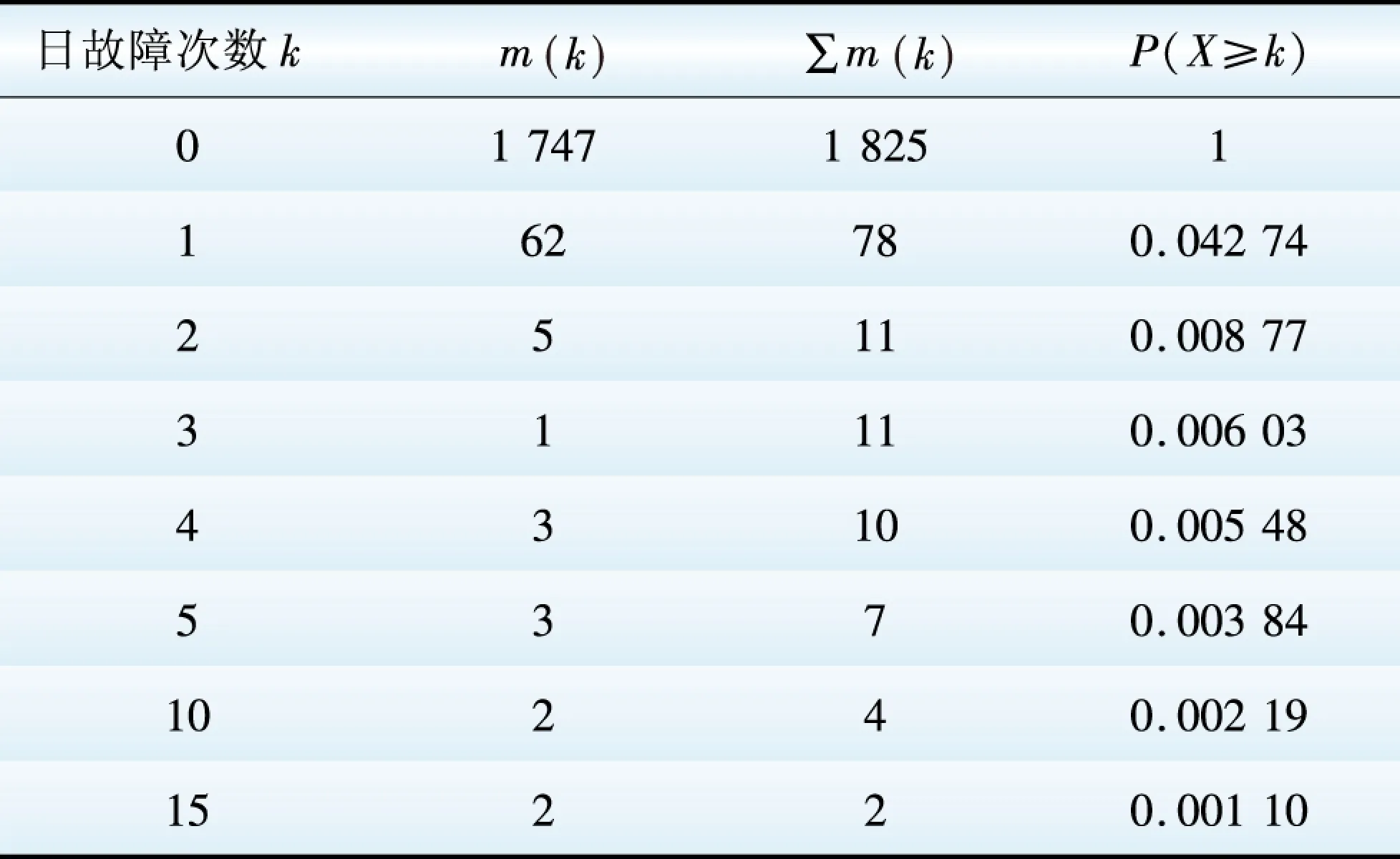
从表1可以看出,以日为时间序列子区间的统计单位时,该输电网在1 825天间隔里发生输电线路故障1天最多15次的机率仅仅为0.11%,1天内出现2次故障的机率仅占0.877%,不到1%;1天内出现1次故障的机率仅占4.27%,绝大多时间记录区间都不发生故障的机率为95.7%。
以日发生故障次数k为横坐标,纵坐标为累计概率P(X≥k),在单对数坐标和双对数坐标下的分布如图2、图3所示。
图2为对累计概率取单对数,8个统计数据点只有1个在95%置信度区间外,统计数据与拟合直线的相关度为0.744 1,且所统计的数据点呈现出尾部后翘,类似有幂律分布特性。
从图3可以看出,以日为时间序列区间,H省500kV输电网日发生故障的次数与其相对应的累计概率P(X≥k)之间的分布关系近似为
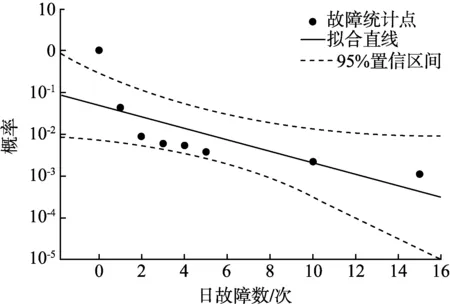
图2 单对数坐标日故障次数的累积概率Fig.2 Cumulative frequency of daily fault in single-logarithmic coordinate
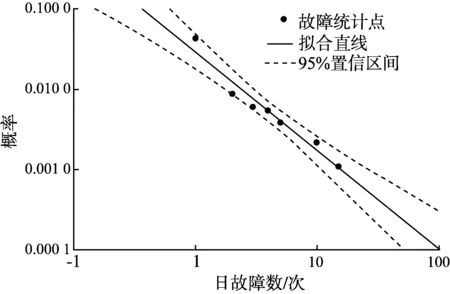
图3 双对数坐标日故障次数的累积概率分布Fig.3 Cumulative probability distribution of daily fault in double-logarithmic coordinate
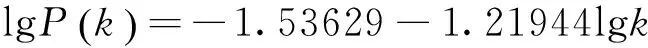
(1)
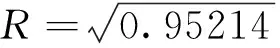
根据上述统计结果,可以观察到H省500kV输电线路日故障次数的时间序列分布并不表现为泊松公布,而是更趋向于满足幂律分布,且具有非线性特征。文献[4]在上述基础上通过探讨故障长时间序列上的自相关性来判断电网的动力学行为是否具有幂律性。
1.2 统计样本的K-S正态性检验
为了更完整地描述输电网故障时间序列的统计分布特性,采用K-S检验方法,对2008~2012年的输电线路故障数据以日为时间序列进行正态性检验,计算结果如表2所示。
从表2可以看出,日故障次数在时间序列上的偏度在15.886 2,远大于0,峰度为305.023,也远大于0,由此可知样本数据明显表现为尖峰厚尾分布,结合图2、图3,可得到H省500kV输电网2008~2012年间的日故障次数在时间序列上并不服从正态分布,而近似服从幂律分布。为了考察H省500kV输电线路故障序列的长程相关性,是否存在异常扩散的可能,以下采用Hurst指数分析法研究500kV输电网故障时序的长程相关性。
表2 以日为单位的故障次数时序统计描述
Table 2 Statistics of fault time series in terms of individual day

2 时序长程相关性分析理论
2.1 R/S时序分析法
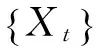
(2)
偏差为
(3)
由式(2)、(3)求得累计偏差:
(4)
其中:1≤i≤n,k=1,2,3,…,n;
极差:
(5)
由式(3)~(5)得到极差与标准差之比为
R/S=CnH
(6)
式中:C为常数;H为Hurst指数。
对式(6)两边取对数并用最小二乘法估算Hurst指数值:
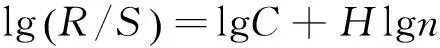
(7)
2.2Hurst指数的形式
计算Hurst指数的目的是为了分析时间序列的统计特性,它可以衡量1个时间序列的统计相关性,其取值区间为(0,1)。Hurst指数有3种取值形式:
(1)当H=0.5时,表明时间序列是标准的“随机游走”,呈独立分布,即事件在长时间发展趋势上是无规律的、不相关的;
(2)当0.5 (3)当0 2.3Hurst指数的显著性检验 Hurst指数虽然可以直接作为自相似性的判断值,但其容易受时间序列中短期记忆、序列数据长度、平衡性等因素的影响。文献[17]给出了Hurst指数显著性检验的经验公式: (8) (9) (10) (11) 根据公式(2)~(7),基于R/S方法计算得到H省500kV输电网5年期间输电线路故障时序的H指数为0.527 083,相应的最小二乘拟合系数为0.902 25,如图4所示。 由图4可以推断H省500kV输电线路的故障时序虽然在一定程度上具有随机性,但总体上表现出长程自相关性,故障的时间行为并不服从泊松分布,而与幂律分布更相似,具有典型的非线性特征,揭示了电网日故障的时间序列具有较好的统计自相似性和长程相关性。 图4 以日为单位的输电线路故障时序Hurst指数Fig.4 Hurst exponent of transmission line fault time series in terms of individual day 图5 基于R/S方法计算的输电线路故障时序 Hurst指数的期望值Fig.5 Expected value of Hurst exponent of transmission line fault time series based on R/S method 因此,可以推断H省500 kV输电线路的故障时序虽然在一定程度上具有随机性,但总体上表现出长程自相关性,故障的时间行为并不服从泊松分布,而与幂律分布更接近,具有典型的非线性特征,揭示了电网日故障的时间序列具有较好的统计自相似性和长程相关性。 表3 输电线路故障频次统计 Table 3 Frequency statistics of transmission line fault 从表3可知,47条输电线路在5年中发生过15次及以上故障的线路仅有2条,占4.25%,根据年统计分析,这条线路故障跳闸次数爆增是在2008年冰灾期间。出现过2次故障的输电线路有15条,占74.47%,还有6条输电线路从未发生过故障跳闸事故,即存在极少数输电线路故障跳闸次数相对较多,绝大多数发生故障的机率较低。 图6 故障线路出现的频次统计Fig.6 Frequency statistics of faulty line occurrence (12) 式(12)中所示拟合优度为R2=0.745 32,即相关系数R=0.863 32。 图7 故障线路出现频次的概率分布Fig.7 Probability distribution of line fault occurrence frequency (13) 式(13)中所示拟合曲线的拟合优度R2=0.931 19,即相关系数R=0.964 98。 由式(12)、(13)可知,H省500kV输电线路故障的空间分布特性总体上表现为近似满足幂律分布,即有些输电线路发生故障次数较多,频率较高、相对比较脆弱;有些输电线路5年间只发生过1、2次故障,发生故障的频次很少;甚至有几条输电线路从未发生过故障,这些线路相对就比较坚强。这说明H省500kV输电网中存在脆弱点,应加强对电网中薄弱点的监测和管理。 (1)以日为时间序列分析500kV输电线路故障分布特性并对其分布特性进行K-S检验,发现日故障序列呈现出尖峰厚尾分布,体现出非线性特征。采用R/S方法计算H指数值大于0.5,且经检验所求结果是显著的,说明输电网故障在时间序列上行为不仅具有非随机性,而且表现出幂律分布特征,在一定程度上具有长程相关性。 (2)通过对H省500kV电网各输电线路故障次数的频次统计分析,发现故障线路出现频次的概率分布近似服从幂律分布,并且各输电线路中发生故障的频次有较明显的差异,某些输电线路相对比较脆弱,在恶劣条件下,短时间内多次爆发故障,也有部分输电线路相对而言鲁棒性较好,5年期间未发生过一次故障。说明电网存在薄弱环节。 总之,H省500kV输电线路故障序列在时间上表现出长程相关性,在空间上以输电线路为分类依据时,具有近似幂律分布特性。因此,研究电网故障的时空分布特性为电网的风险管理和风险预测提供了辅助决策的依据。 致 谢 本文中实验方案的制定和实验数据的测量记录工作是在湖南省电力公司检修公司业娅、彭熹、贺丁丁等工作人员的大力支持下完成的,在此向他(她)们表示衷心的感谢。 [1]梁志峰,葛睿,董昱,等.印度“7.30”、“7.31”大停电事故分析及对我国电网调度运行工作的启示[J].电网技术,2013,37(7):1841-1848.LiangZhifeng,GeRui,DongYu,etal.Analysisoflarge-scaleblackoutoccurredonJuly30andJuly31,2012inIndiaanditslessonstoChina’spowergriddispatchandoperation[J].PowerSystemTechnology,2013,37(7):1841-1848. [2]陈亦平,洪军.巴西“11.10”大停电原因分析及对我国南方电网的启示[J].电网技术,2010,34(5):77-82.ChenYiping,HongJun.AnalysisoncausesofblackoutoccurredinBrazilianpowergridonNov.11,2009andlessonsdrawnfromittoChinaSouthernpowergrid[J].PowerSystemTechnology,2010,34(5):77-82. [3]毛安家,张戈力,吕跃春,等.2011年9月8日美墨大停电事故的分析及其对我国电力调度运行管理的启示[J].电网技术,2012,36(4):74-78.MaoAnjia,ZhangGeli,LüYuechun,etal.Analysisonlarge-scaleblackoutoccurredinSouthAmericaandNorthMexicointerconnectedpowergridonSep8,2011andlessonsforelectricpowerdispatchinginChina[J].PowerSystemTechnology,2012,36(4):74-78. [4]梅生伟,薛安成,张雪成.电力系统自组织临界特性与大电网安全[M].北京:清华大学出版社,2009:3-8. [5]Rosas-CasalsM,ValverdeS,SoleRV.TopologicalvulnerabilityoftheEuropeanpowergridundererrorsandattacks[J].InternationalJournalofBifurcationandChaos,2007,17(7):2465-2475. [6]AlbertR,AlbertI,NakaradoGL.StructuralvulnerabilityoftheNorthAmericanpowergrid[J].PhysicalReviewE,2004,69(2):025103(1-4). [7]郭亦坚.外部风险源作用下电力系统自组织临界性分析[J].电力建设,2013,34(11):67-70.GuoYijian.Analysisofself-organizedcriticalityofpowersystemunderexternalrisks[J].ElectricPowerConstruction,2013,34(11):67-70. [8]任惠,熊吉,DavidWatts,等.基于历史故障记录数据的电网连锁故障规模概率分布研究[J].电力系统保护与控制,2014,42(7):23-30.RenHui,XiongJi,DavidWatts,etal.Studyonthehistoricaloutagedatabasedprobabilitydistributionofcascadinglinefailuresinaregionalpowergrid[J].PowerSystemProtectionandControl,2014,42(7):23-30. [9]谭米,苏盛,易文韬.配电网故障统计特性其及形成机理分析[J]. 电力系统及其自动化学报,2015,27(1):1-4,12.TanMi,SuSheng,YiWentao.Statisticaldistributionofpowersystemfaultinpowergridandanalysisofitsmechanism[J].ProceedingoftheCSU-EPSA,2015,27(1):1-4,12. [10]刘文颖,但扬清,朱艳伟,等.电网运行断面的自组织临界态辨识和量化分析[J]. 电网技术, 2014,38(8):2076-2081.LiuWenying,DanYangqing,ZhuYanwei,etal.Identificationandquantitativeanalysisofself-organizedcriticalstateinrunning-gridsection[J].PowerSystemTechnology, 2014,38(8):2076-2081. [11]LiuLiu,ChaiJidong,QiHairong,etal.Powergriddisturbanceanalysisusingfrequencyinformationatthedistributionlevel[C]//2014:523-528. [12]李孝杰,陈兴宇.张家界电网故障的统计分布特性及其机理分析[J].华中电力,2011,24(3):39-42.LiXiaojie,ChenXingyu.StatisticsoffaultsinZhangjiajiepowergridanditsmechanism[J].CentralChinaElectricPower,2011,24(3):39-42. [13]DuanXZ,SuS.Self-organizedcriticalityintimeseriesofpowersystemfault,itsmechanism,andpotentialapplication[J].IEEETransactiononPowerSystems,2010,25(4):1857-1864. [14]何俊,庞松龄,禹冰,等.基于容量介数指标的电网脆弱线路识别[J].电力系统保护与控制,2013,41(8):30-35.HeJun,PangSongling,YuBing,etal.Vulnerablelineidentificationofpowergridbasedoncapacitybetweennessindex[J].PowerSystemProtectionandControl,2013,41(8):30-35. [15]徐立新,杨建梅,潮铸,等.电网故障时间间隔的统计分布及非线性特征分析[J]. 电网技术,2013,37(12):3482-3488. XuLixin,YangJianmei,ChaoZhu,etal.Statisticaldistributionandnonlinearcharacteristicanalysisoffaulttimeintervalsinpowergrids[J].PowerSystemTechnology,2013,37(12):3482-3488. [16]晁岱峰,杨军选,苏盛,等.濮阳配电网故障的自组织临界性及其诱因[J].电网技术,2011,35(1):72-75.ChaoDaifeng,YangJunxuan,SuSheng,etal.Self-organizedcriticalityanditscauseoffaultinPuyangdistributionsystem[J].PowerSystemTechnology,2011,35(1):72-75. [17]宣蕾,卢锡城,于瑞厚,等.网络威胁时序的自相似性分析[J].通信学报,2008,29(4):45-50.XuanLei,LuXicheng,YuRuihou,etal.Self-similarityanalysisofnetworkthreattimeseries[J].JournalonCommunications,2008,29(4):45-50. (编辑:张媛媛) Spatial-Temporal Characteristics of 500 kV Transmission Line Fault LUO Jie1,2,JIANG Tiezheng1,LIANG Yongchao2,MA Rui1 (1. College of Electrical and Information Engineering, Changsha University of Science and Technology, Changsha 410076, China;2. Hunan Electric Examine and Repair Company, Changsha 410002, China) With the development of power system communication automation, various kinds of information collection systems have been widely used, which is beneficial to analyze the spatial-temporal characteristics of power grid faults. Taking 500 kV transmission network in H province as example, this paper researched the long-time behavior characteristics of 500 kV transmission line faults in recent 5 years. Firstly, on the time series level of transmission line fault, statistical analysis was carried out on the interrelation between fault timing (unit: day) and fault cumulative frequency and probability under same time point. Kolmogorov-Smirnov (K-S) method was adopted to testify the normality of the distribution, and Hurst exponent based on time series of 500 kV transmission network in H province during 5 years was calculated according to R/S time series analysis. Thereby the long-term correlation under time series was estimated. Then, on the level of space, statistical analysis was carried out on the interrelation between fault times of each 500 kV transmission line in H province during 5 years and its fault cumulative frequency and probability, and it was proved that transmission line faults coincided with power-law distribution characteristic. The research on the spatial-temporal distribution characteristics can provide the basis of assistant decision for the risk management and prediction of power system. transmission line fault; spatial-temporal distribution; power-law distribution; Hurst exponent; R/S analysis method 国家自然科学基金项目(51277015)。 TM 711 A 1000-7229(2015)06-0046-07 10.3969/j.issn.1000-7229.2015.06.008 2015-03-25 2015-04-25 罗杰(1983),男,硕士研究生,工程师,主要从事电力系统分析、运行与控制方面的研究工作; 蒋铁铮(1965),男,博士,副教授,硕士研究生导师,主要从事电力系统稳定分析与非线性控制的研究工作; 梁勇超(1972),男,硕士,高级工程师,主要从事超高压输变电运检、继电保护方面的管理工作; 马瑞(1971),男,博士,教授,硕士研究生导师,主要从事电力系统分析与控制、低碳电力和电力大数据方面的研究工作。 Project Supported by National Natural Science Foundation of China (51277015).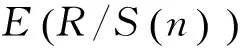
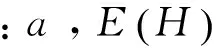
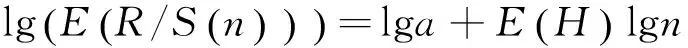
3 输电线路故障时序的Hurst指数分析及显著性检验
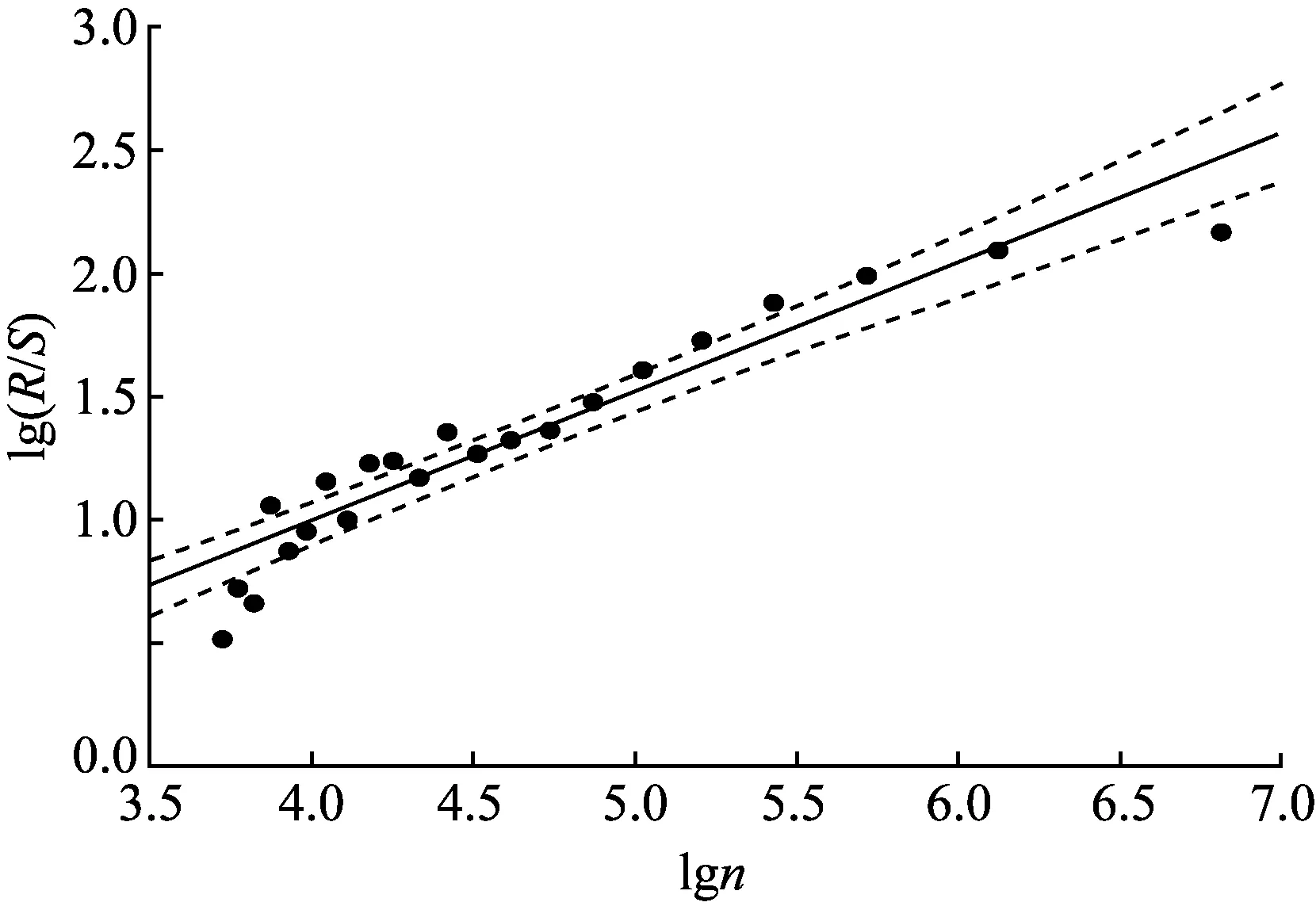
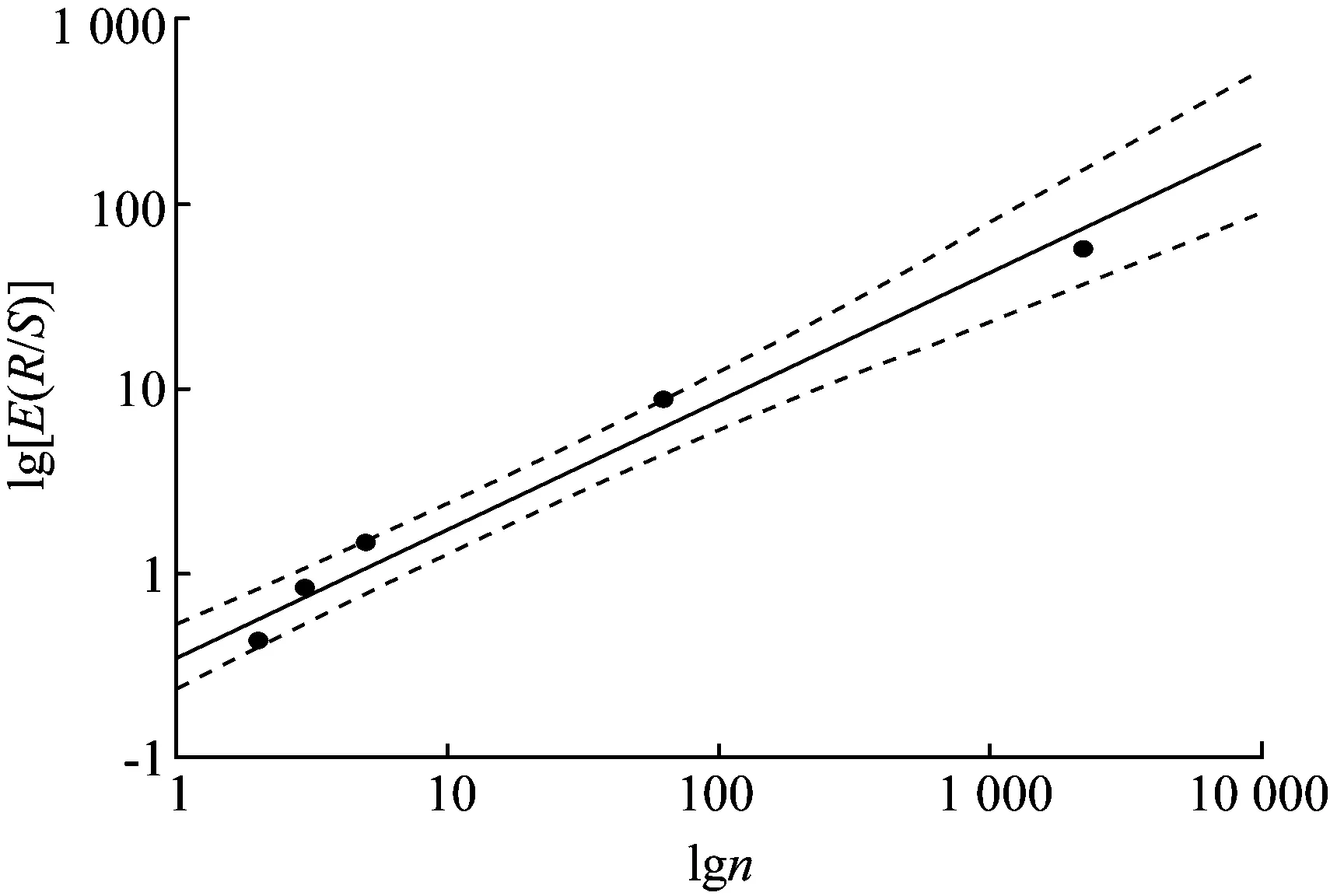
4 输电线路故障的空间分布特性分析
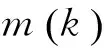

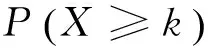
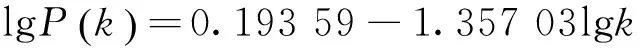
5 结 论
