具有简单G2条件的类Bézier曲线曲面

严兰兰， 韩旭里， 黄 涛

（1.东华理工大学 理学院，江西 南昌330013；2.中南大学 数学与统计学院，湖南 长沙410083）

Bézier方法是计算机辅助几何设计中表示曲线曲面的重要方法之一，它具有很多优点，但也存在不足，例如，给定控制顶点，Bézier曲线曲面的形状便唯一确定，要想修改其形状，必须调整控制顶点，重新计算曲线曲面方程。对于这个不足，有大量文献提出了解决办法［1－7］，这些文献的共同思想是构造含参数且具备Bernstein基函数基本性质的新的基函数。很自然地，由新的基函数定义的曲线曲面具备Bézier曲线曲面的基本性质之外，还具备了形状可调性。此外，Bézier方法无法精确表示工程上常用的除抛物线以外的圆锥曲线曲面和超越曲线曲面。对于这个不足，也有很多文献提出了解决办法［8－16］，这些文献的思想是在非多项式空间，如代数三角混合函数空间［8－12］、代数双曲混合函数空间［13－16］上构造具备Bernstein基函数基本性质的新的基函数。由此定义的曲线曲面在具备Bézier曲线曲面基本性质的同时，还能表示 椭 圆 （圆）［8－12］、心 脏 线［10］、摆 线［11］、心 形线［11］、双曲线［13－16］、悬链线［15－16］等，而且有的还具备形状可调性［9，11－16］。

注意到单一的Bézier曲线曲面无法表示复杂的形状，所以在工程实际中，常需将多条Bézier曲线或多张Bézier曲面进行组合，为保证组合曲线曲面的光滑性，相邻Bézier曲线曲面的控制顶点间需满足一定的光滑性条件，通常对光滑性的要求越高，条件越复杂。对于普通Bézier曲线和大多数扩展Bézier曲线而言，当前一条曲线的最后一个控制顶点和后一条曲线的第1个控制顶点重合（称为公共控制顶点）时，2条曲线位置（G0或C0）连续。在此基础上，当前一条曲线的倒数第2个控制顶点、2条曲线的公共控制顶点以及后一条曲线的第2个控制顶点3点共线时，2条曲线在公共点处达到一阶几何（G1）连续。因此一般情况下，2条曲线在拼接时的G0连续条件中涉及2个控制顶点，G1连续条件中涉及4个控制顶点，如此类推，连续阶越高，涉及的控制顶点数目越多。在工程实际中，二阶几何（G2）连续可以满足大多数的要求，因此考虑能否使组合曲线在满足G1连续性条件下达到G2连续。为实现该目标，这里给出了n（n≥2）次Bézier曲线的扩展曲线，新曲线不仅具备形状可调性，而且还可以在相对简单的条件下实现G2光滑拼接。

1 基函数及其性质

1.1 基函数的定义

定义1 设λ∈（－3，1］，对t∈［0，1］，称（1）式为带形状参数λ的2阶类Bernstein基函数。

记s＝sin（πt／2t），c＝cos（πt／2），对任意的整数n（n≥3），称由递推公式（2）定义的函数bni（t）（i＝0，1，…，n）为带形状参数λ的n阶类Bernstein基函数。

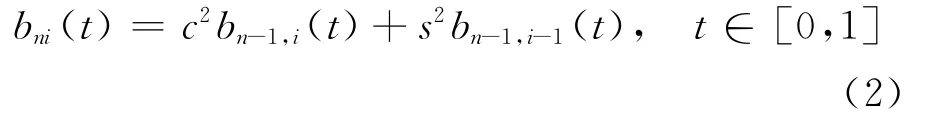
规定当l＜0或l＞k时，（2）式右端的bkl（t）等于0。

为了简洁，称上面定义的函数bni（t）（i＝0，1，…，n；n≥2）为n阶λ－Bernstein基，在不至于引起混淆时，下文中将bni（t）简记为bni。

图1所示为带不同参数的2～5阶λ－Bernstein基，图中实线均为参数λ＝－2时的基函数，点线均为参数λ＝－0.5时的基函数，虚线均为参数λ＝1时的基函数。

图1 2～5阶λ－Bernstein基

1.2 基函数的性质

λ－Bernstein基具有类似于Bernstein基的一些良好性质。

（1）非负性。当λ∈（－3，1］时，n阶λ－Bernstein基bni≥0（i＝0，1，…，n；n≥2）。

证明 采用数学归纳法。当n＝2时，λ－Bernstein基可以写成：

其中，B4i（i＝0，1，…，4）为4次 Bernstein基函数。显然，当λ∈（－3，1］时，（1－λ）／4≥0，（3＋λ）／4＞0，又因4次Bernstein基函数非负，因此2阶λ－Bernstein基也非负。假设r阶λ－Bernstein基非负，当n＝r＋1时，由（2）式有：

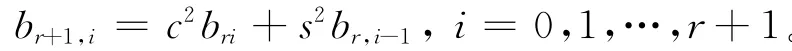
由归纳假设以及c2≥0、s2≥0的事实，可知r＋1阶λ－Bernstein基也非负。

证明 采用数学归纳法。当n＝2时，由（3）式有：

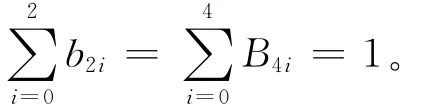
假设r阶λ－Bernstein基满足规范性，当n＝r＋1时，由（2）式有：

这表明r＋1阶λ－Bernstein基也满足规范性。

（3）对 称 性。bni（t）＝bn，n－i（1－t），这 里i＝0，1，…，n，n≥2，t∈［0，1］。

证明 采用数学归纳法。当n＝2时，由（1）式或（3）式易知：

b2i（t）＝b2，2－i（1－t）， i＝0，1，2。

假设r阶λ－Bernstein基满足对称性，当n＝r＋1时，由（2）式可得：

这表明r＋1阶λ－Bernstein基也满足对称性。（4）端点性质。对i＝0，1，…，n（n≥2），有

证明 采用数学归纳法证明（4）式正确。当n＝2时，由（1）式经过简单的计算易知（4）式中结论正确。假设当n＝r时（4）式中结论正确，当n＝r＋1时，由（2）式可得：

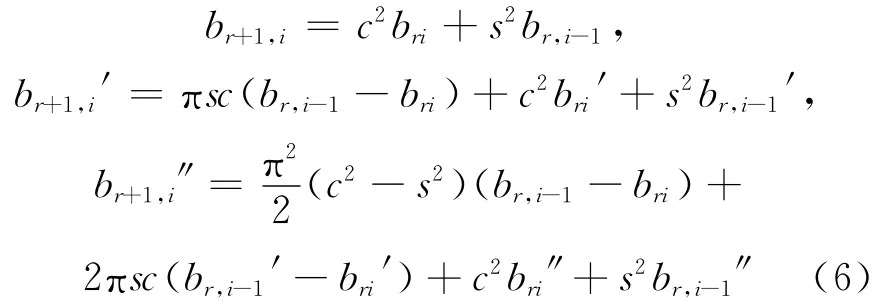
在（6）式中令t＝0可得：

故当n＝r＋1时（4）式中结论也正确。另外，由bni（t）＝bn，n－i（1－t）可得：

bni′（t）＝－bn，n－′i（1－t），bni″（t）＝bn，n－i″（1－t）。

故

由（4）式、（7）式易知（5）式正确。

证明 充分性是显然的，下面用数学归纳法证明必要性。假设：

其中，ai∈R（i＝0，1，2）。将（3）式代入（8）式并整理得：

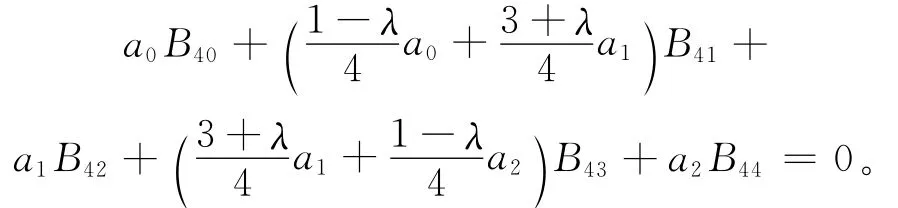
由4次Bernstein基函数的独立性，可知：

易知此方程组的解为ai＝0（i＝0，1，2）。这表明2阶λ－Bernstein基线性无关。

假设r阶λ－Bernstein基线性无关，接下来证明r＋1阶λ－Bernstein基也线性无关。假设：

其中，ai∈R（i＝0，1，…，r＋1），将（2）式代入（9）式可得：

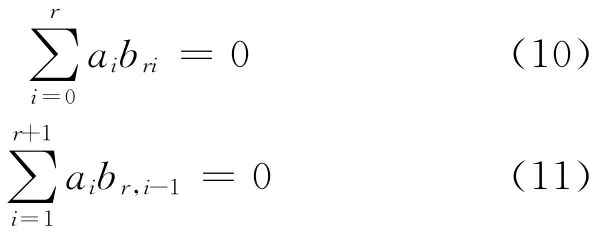
由t的任意性知：由归纳假设和（10）式可知ai＝0（i＝0，1，…，r）。由归纳假设和（11）式可知ai＝0（i＝1，2，…，r＋1）。故对所有的i＝0，1，…，r＋1，有ai＝0，表明r＋1阶λ－Bernstein基也线性无关。

2 曲线及其性质

2.1 曲线的定义与性质

定义2 给定n＋1个控制顶点Vi∈Rd（d＝2，3；i＝0，1，…，n；n≥2）与参数λ∈（－3，1］，称（12）式为带形状参数λ的n阶类Bézier曲线，简称n阶λ－Bézier曲线。

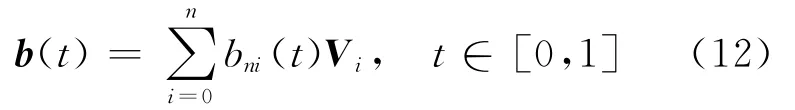
图2～图5所示分别为带不同参数的2～5阶λ－Bézier曲线（实线，从上到下依次取参数λ＝1，－1，－2.9）与普通2～5次Bézier曲线（虚线）。从图中可看出，在一定的参数取值范围内，λ－Bézier曲线对控制多边形的逼近性优于Bézier曲线。

图2 2阶λ－Bézier曲线与2次Bézier曲线

图3 3阶λ－Bézier曲线与3次Bézier曲线

图4 4阶λ－Bézier曲线与4次Bézier曲线

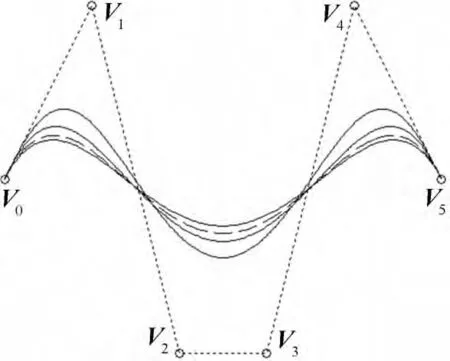
图5 5阶λ－Bézier曲线与5次Bézier曲线

由λ－Bernstein基的性质，易知λ－Bézier曲线具有类似于Bézier曲线的一些性质。

（1）凸包性。由λ－Bernstein基的非负性和规范性可知，λ－Bézier曲线位于其控制顶点形成的凸包内。

（2）几何不变性与仿射不变性。由λ－Bernstein基的规范性可知，一方面，λ－Bézier曲线的形状仅依赖于控制顶点，几何变换不改变曲线的形状；另一方面，对控制多边形进行缩放或错切等仿射变换，所对应的新曲线就是原曲线经过相同仿射变换后的曲线。

（3）对称性。由λ－Bernstein基的对称性可知，取相同的参数λ时，由控制多边形V0V1…Vn和VnVn－1…V0所生成的曲线形状是相同的，只是方向相反。

（4）端点性质。由λ－Bernstein基的端点性质和λ－Bézier曲线的表达式可知：

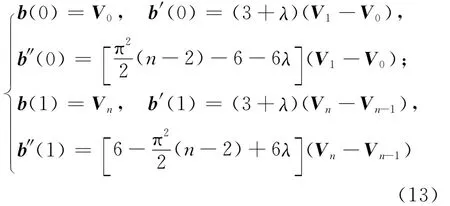
（5）形状可调性。由于λ－Bernstein基中含有参数λ，选择不同的λ值，可以得到不同的基函数，因此即使固定控制顶点，依然可以通过改变参数λ的值来调整λ－Bézier曲线的形状。

2.2 组合曲线的连续性

为了方便，这一部分用bni（t；λ）表示带参数λ的λ－Bernstein基。

定理1 设有m阶λ－Bézier曲线b1（t）＝与n阶λ－Bézier曲 线b2（t）＝，若有（14）式成立，则2条曲线G2连续。

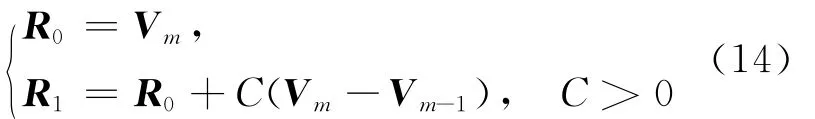
证明 由（13）式可知：

在（14）式所给条件下，有

其中

故2条曲线G2连续［17］。

对于普通Bézier曲线和大多数文献中给出的扩展Bézier曲线而言，在（14）式所给条件下，相邻曲线间只能达到G1连续，而这里给出的λ－Bézier曲线却能达到G2连续。另外，由于（14）式与λ－Bézier曲线中的参数无关，所以在G2连续的组合λ－Bézier曲线中，各曲线段可以取不同的参数，因此曲线段中的参数可以说是局部参数，可以用于局部地调整曲线的形状而不至于破坏曲线的连续性。

图6所示为由3阶λ－Bézier曲线（取参数λ＝0）、2阶λ－Bézier曲线（从上到下依次取参数λ＝－2.8，－0.9，1）、4阶λ－Bézier曲线（取参数λ＝0）构成的G2连续的组合曲线。

图6 G2连续的组合λ－Bézier曲线

3 曲面及其性质

定义3 给定（m＋1）×（n＋1）个呈拓扑矩形阵列的控制点Vij∈R3（i＝0，1，…，m；j＝0，1，…，n；m，n≥2），以及参数λu，λv∈（－3，1］，称（15）式为带形状参数λu、λv的m×n阶类Bézier曲面，简称m×n阶λ－Bézier曲面。λ－Bézier曲面具有与λ－Bézier曲线类似的性质，如凸包性、几何不变性、对称性、形状可调性等。另外，关于组合λ－Bézier曲面的连续性，有下面的结论。

定理2 设有m×n1阶λ－Bézier曲面与m×n2阶λ－Bézier曲面：

若

其中，i＝0，1，…，m，则2张曲面G2连续。

证明 由（4）式、（5）式和（15）式可以得到：

在（17）式所给条件下，有

其中

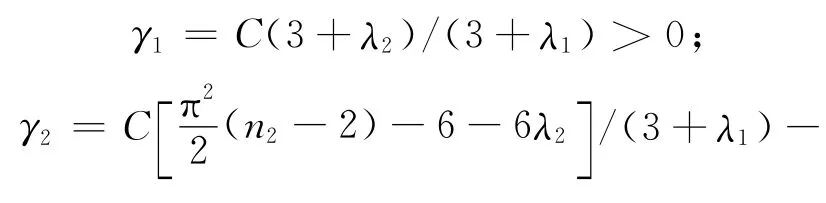
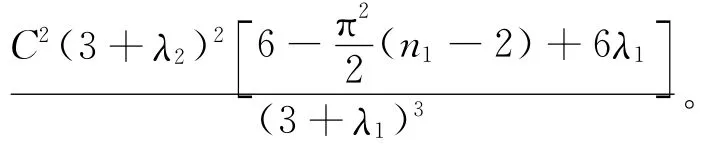
故2张曲面G2连续。

图7所示为在相同控制网格下，通过选择不同的形状参数得到的由3×3阶λ－Bézier曲面构成的2张G2连续的组合曲面。图7a中λi＝0（i＝0，1，2），图7b中λi＝－2.5（i＝0，1，2）。

图7 G2连续的组合λ－Bézier曲面

4 结束语

本文给出的λ－Bézier曲线具有很多优点：① 具备Bézier曲线的凸包性、几何不变性、对称性等基本性质；② 可以在不改变控制顶点的情况下，通过选择合适的参数λ来得到满意的形状；③ 在构造组合曲线时，只要相邻曲线的控制顶点之间满足普通Bézier曲线的G1光滑拼接条件，曲线间便可以达到G2光滑拼接。而λ－Bézier曲面在具备Bézier曲面的基本性质之外，也具有形状可调性，易于实现G2光滑拼接这2个良好的性质。文中图例说明了本文方法的正确性与有效性，因此λ－Bézier曲线曲面可望在工程实际中发挥一定的作用。当然λ－Bézier曲线曲面也有不足，现有文献中一些以代数三角混合函数作为基函数的扩展Bézier曲线曲面能精确表示椭圆、椭球面等，而λ－Bézier曲线曲面还不具备这一性质。所以下一步将尝试构造新的代数三角混合基，使得由之定义的曲线曲面在具备λ－Bézier曲线曲面的所有性质之外，还能精确表示一些圆锥曲线曲面或超越曲线曲面。

［1］ Wang Wentao，Wang Guozhao.Bézier curves with shape parameter［J］.Journal of Zhejiang University Science A，2005，6（6）：497－501.

［2］ Han Xi’an，Ma Yichen，Huang Xili.A novel generalization of Bézier curve and surface ［J］.Journal of Computational and Applied Mathematics，2008，217（1）：180－193.

［3］ Yang Lianqiang，Zeng Xiaoming.Bézier curves and surfaces with shape parameters［J］.International Journal of Computer Mathematics，2009，86（7）：1253－1263.

［4］ Qin Xinqiang，Zhang Nianjuan，Hu Gang.A novel Bézier curve with multiple shape parameters［C］／／2010 3rd IEEE International Conference on Computer Science and Information Technology，2010，7：494－498.

［5］ Chen Jie，Wang Guojin.A new type of the generalized Bézier curves［J］.Applied Mathematics：A Journal of Chinese Universities，2011，26（1）：47－56.

［6］ Yan Lanlan，Liang Jiongfeng.An extension of the Bézier model［J］.Applied Mathematics and Computation，2011，218（6）：2863－2879.

［7］ 严兰兰，邬国根.Bézier方法的新扩展［J］.合肥工业大学学报：自然科学版，2013，36（5）：625－631.

［8］ Chen Qinyu，Wang Guozhao.A class of Bézier－like curves［J］.Computer Aided Geometric Design，2003，20（1）：29－39.

［9］ Han Xi’an，Ma Yichen，Huang Xili.The cubic trigonometric Bézier curve with two shape parameters［J］.Applied Mathematics Letters，2009，22（2）：226－231.

［10］ 程 荣，潘永娟，周明华.一类三角多项式曲线的性质及应用［J］.计算机工程与应用，2010，46（7）：39－43.

［11］ 师利红，张贵仓.三次 TC－Bézier曲线的新扩展［J］.计算机工程与应用，2011，47（4）：201－204.

［12］ Han Xuli，Zhu Yuanpeng.Curve construction based on five trigonometric blending functions ［J］.BIT Numerical Mathematics，2012，52（4）：953－979.

［13］ 苏本跃，盛 敏.基于双曲函数的Bézier型曲线曲面［J］.计算机工程与设计，2006，27（3）：370－372.

［14］ 谢 进，檀结庆.多形状参数的二次双曲多项式曲线［J］.中国图象图形学报，2009，14（6）：1206－1211.

［15］ Chen Sugen，Huang Youdu.Hyperbolic Bézier curves with multiple shape parameters ［J］.Journal of Engineering Graphics，2009，30（1）：75－79.

［16］ 张锦秀，檀结庆.代数双曲Bézier曲线的扩展［J］.工程图学学报，2011，32（1）：31－38.