带有交叉扩散项的捕食－食饵模型的全局分歧

张晓晶，容跃堂

（西安工程大学 理学院，陕西 西安 710048）

0 引 言

通过建立数学模型来描述生物系统的特性是数学应用领域的一个重要组成部分，捕食－食饵模型是数学模型的有机组成，吸引了众多学者的关注，并取得了许多研究结果［1－4］。

文献［5－6］提出了带有B－D功能反应函数的捕食系统：

其中，u、v分别表示食饵与捕食者的种群密度。引入无量纲参数：

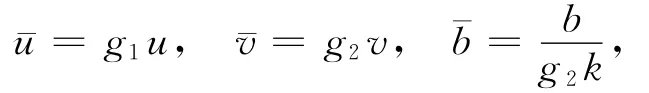
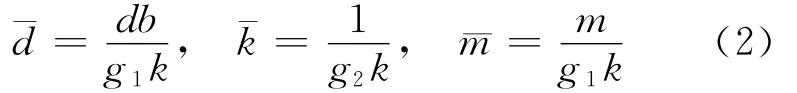
并考虑到空间的不均匀分布，模型可化为如下反应扩散系统：

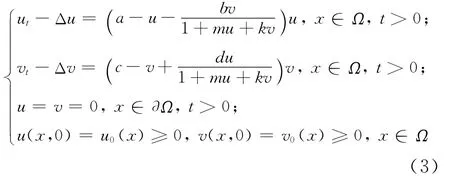
在经典的反应扩散方程中，种群扩散往往是因为种群的随机移动，然而在某些生态系统中，种群间的相互影响在种群扩散中也起着非常重要的作用，因此本文考虑一类带有交叉扩散项的捕食－食饵模型：

其中，Ω为Rn中的有界开区域，且边界∂Ω充分光滑；u、v分别为食饵和捕食者的密度；参数a、c、d均为正常数；m为非负常数；b可正可负，b＞0表示捕食者有其他的食物来源。

对无交叉扩散情形，文献［7］通过计算不动点的指标和特征值的性质得到正解的存在性与唯一性。本文讨论带有交叉扩散的情况，给出了局部分歧解的存在性，并将局部分歧延拓为整体分歧。

1 分歧正解的存在性

与系统（4）式对应的平衡态问题为：

对于问题（5）式的解（u，v），若在Ω中u＞0，v＞0，则称它为正解，相应的称（0，0）为平凡解。如果（u，v）中只有1个分量为0，则称它为半平凡解。考虑特征值问题：

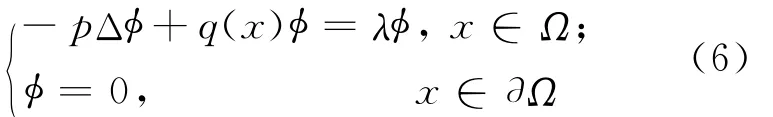
由文献［8］知λi（p，q）是简单的，且关于p和q（x）均严格单调递增，简记λi（1，q）为λi（q），λi（0）为λi。

考虑单个方程：

由文献［8］知：若a≤λ1（q（x）），则u＝0是方程（7）式的唯一非负解；而当a＞λ1（q（x））时，方程（7）式存在唯一正解。当q（x）＝0，a＞λ1时，把这个唯一正解记为θa。特别地，θa关于a严格单调递增，连续可微，且对任意x∈Ω，0＜θa＜a，引入新函数：

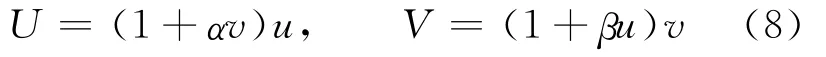
则（u，v）≥0和（U，V）≥0之间存在一一对应关系，那么（5）式等价于半线性椭圆系统：

其中，u、v为（U，V）的函数。显然（9）式存在平凡解（0，0）。此外，若a＞λ1，则（9）式存在半平凡解（θa，0）；若b＞λ1，则（9）式存在半平凡解（0，θb）。令C0）＝｛U∈C（）：U｜∂Ω＝0｝，并定义算子Law＝－Δw－（a－2θa）w，w∈C2（Ω）∩C0）。易知，算子La的所有特征值都是正的，这就说明La可逆。

引理2 设b＞max｛λ1，d／β｝ ，则存在唯一的a＝a＊（b）∈（λ1，∞），满足：

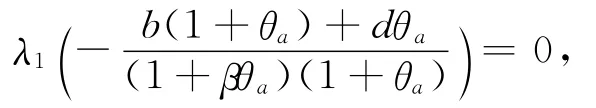
且a＝a＊（b）关于b严格单调递增。

证明 令

显然A（λ1，b）＝λ1（－b）＝λ1－b＜0。由于当a→∞时θa→∞，从而有。

经计算得：

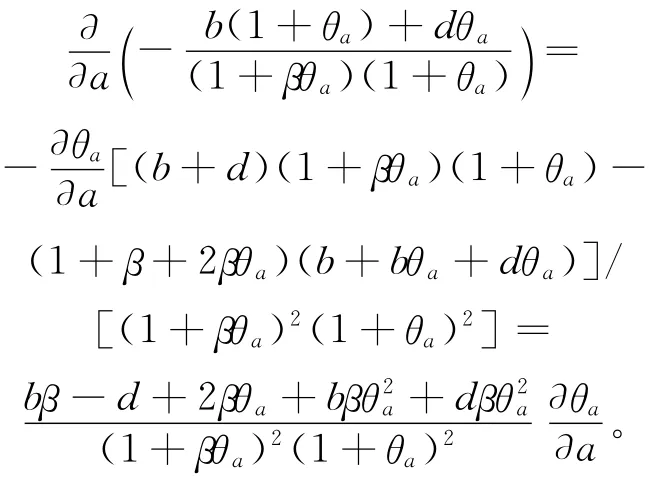
由于b＞d／β，且有q→λ1（q）：C）→R和a→θa：［λ1，∞）→C2（Ω）∩C0）均严格单调递增，从而可知A（a，b）关于a严格单调递增，因此存在唯一的a＝a＊（b）＞λ1，使得A（a＊（b），b）＝0。

等式A（a＊（b），b）＝0两边关于b求导得Aa（a＊（b），b）·a′＊（b）＋Ab（a＊（b），b）＝0，由于Ab（a，b）＜0，结合Aa（a，b）＞0知a′＊（b）＞0，即a＝a＊（b）关于b严格单调递增。

类似可证明下面的引理3。

引理3 设b＞λ1，则存在唯一的a＝a＊（b）

设b＞λ1，由引理2知，存在唯一的a＊＞λ1使得，设 ≥0满足：ψ＊

另一方面，由引理3知，存在唯一的a＊＞λ1使得。不妨设 满足：φ＊

以a为分歧参数，利用Crandall－Rabinowitz局部分歧定理，给出问题（9）式发自半平凡解（θa，0）和（0，θb）的局部分歧正解的存在性。

令

其中，u、v均为（U，V）的函数。

将（9）式在（U，V）＝（θa，0）处 Taylor展开可得：

其中，偏导数均为（θa，0）处的导数值，ρi（U－θa，V）满足。

对（8）式两端关于（U，V）求导得：

s（ψ＊＋Ψ1（s）））：0＜s≤δ｝。

Ψ （s））是 C1连续函数，且满足a（0）＝a，

1＊Φ1（0）＝0，Ψ1（0）＝0，∫ΩΨ1ψ＊dx＝0。

显然有F（a；0，0）＝0。

Frechlet导数为L（a＊；0，0），经计算，L（a＊；0，0）·

如果ψ≡0，则由算子La＊可逆知φ≡0，因此ψ不恒为0，又因

因此，算子L（a＊；0，0）的核空间N（L（a＊；0，0））＝span｛U0｝，U0＝（φ ，ψ ）T，令 L＊（a；0，0）为

＊＊＊L（a＊；0，0）的自伴算子，类似可得N（L＊（a＊；0，0））＝span｛U＊｝，U＊＝（0，ψ＊）T。由Fredholm选择公理知：

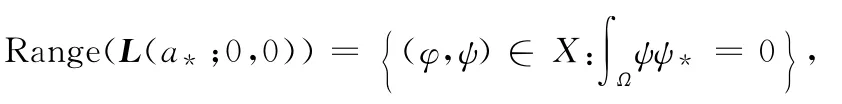
因此可得：

dim N（L（a＊；0，0））＝1，codimR（L（a＊；0，0））＝1。

用反 证 法 证 明 L1（a＊；0，0）· （φ＊，ψ＊）∉

R（L（a＊；0，0））。假 设 存 在 （h，k）∈ X 使 得L1（a＊；0，0）·（φ＊，ψ＊）＝L（a＊；0，0）·（h，k），则

那么有：

两边同时乘以ψ＊，分部积分得：

由于bβ＞d及θa关于a严格单调递增，（12）式左边大于0，矛盾。

因此由 Crandall－Rabinowitz局部分歧定理［9］知，存在充分小的δ＞0及C1连续曲线（a（s）；Φ1（s），Ψ1（s））：（－δ，δ）→R×X 满足a（0）＝a＊，Φ1（0）＝0，Ψ1（0）＝0，Φ1（s），Ψ1（s）∈Z，使得（a（s）；（s），V（s））＝ （a（s）；s（φ＊＋Φ1（s）），s（ψ＊＋Ψ1（s）））是F（a（s）；（s），V（s））的零点，其中X＝Z8N（L（a＊；0，0）），由于＝U－θa，因此可得到发自（a＊；θa＊，0）的局部分歧正解Γ＊。

同理可得到发自半平凡解分支（a；0，θb）的局部分歧正解。

定理2 设a，b＞λ1，则（a＊；0，θb）∈R＋×X为（9）式的分歧点，且在（a＊；0，θb）的邻域内存在正解，即

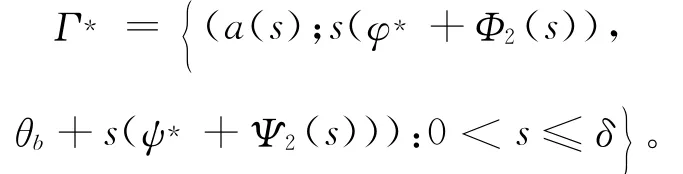
2Φ2（0）＝0，Ψ2（0）＝0，∫ΩΨ2φ＊dx＝0，且有：

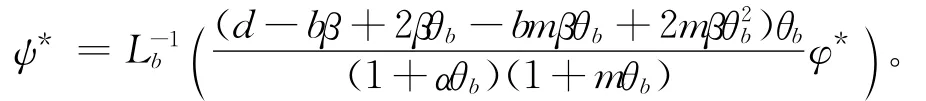
2 局部分歧解的延拓

利用文献［10－11中的方法，并结合全局分歧理论，可将局部分歧延拓为全局分歧。

定理3 定理1中的局部分歧正解Γ＊可以延拓为全局分歧，且存在常数充分大，使得当α≥时，全局分歧曲线随参数a到无穷。

证明 在（11）式中，令K 为（－Δ）－1，则其等价于：

定义算子T：R＋×X→X为：

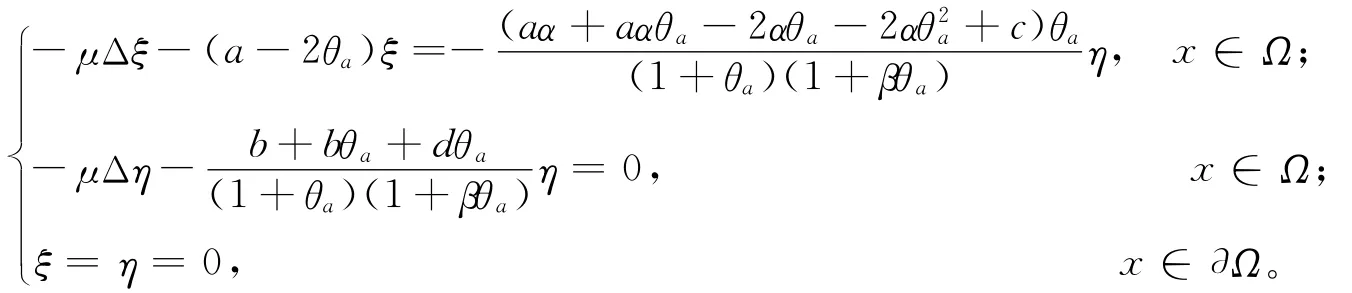
如果η≡0，那么由算子（－μΔ－a＋2θa）可逆知ξ≡0，矛盾。因此η不恒为0。令qa（x）＝，那么一定存在某个i（i＝1，2，…），使得λi（μ，qa）＝0。∀i，λi（μ，qa）关于μ≥1和a＞λ1均严格单调递增，并且λi（μ，qa）可排列为λ1（μ，qa）＜λ2（μ，qa）≤λ3（μ，qa）≤…→∞。特别地，λ1（1，qa）＝0。另外，若存在某个i使λ（μ，q）＝0，则μ≥1必是iaT′（a）的特征值。因此，μ≥1是T′（a）的一个特征值的充分必要条件是存在某个i＝1，2，…，使得λi（μ，qa）＝0。

令a＞a＊，∀μ≥1，i≥2，有λi（μ，qa）＞λ1（μ，qa＊）＞λ1（1，qa＊）＝0，因此，T′（a）没有大于或等于1的特征值，此时i（T（a；·），0）＝1。

设存在充分小的ε，使得a＊－ε＜a＜a＊且λ2（μ，qa＊－ε）≥λ1（μ，qa＊），则 ∀μ≥1，i≥2，有λi（μ，qa）≥λ2（μ，qa）＞λ2（μ，qa＊－ε）≥λ1（μ，qa＊）≥λ1（1，qa＊）＝0，因为λ1（1，qa）＜λ1（1，qa＊）＝0，limλ1（μ，qa）＝＋∞，且λ1（μ，qa）关于μ 单调递

μ→∞

增，因此存在唯一的μ1＞1，使得λ1（μ1，qa）＝0，从而得出：

其中

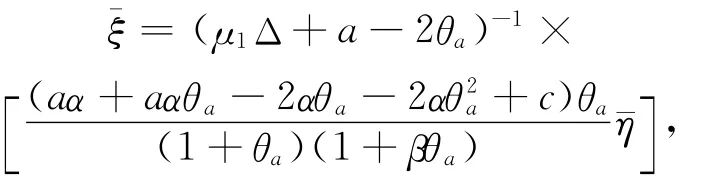
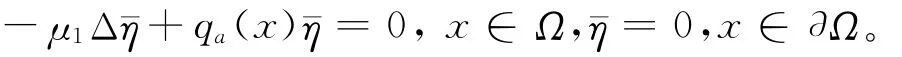
接下来证明μ1的代数重数是1，只需证明R（μ1I－T′（a））∩N（μ1I－T′（a））＝0。事实上，假设∃（ξ，η）∈X，使得（μ1I－T′（a））·（ξ，η）＝）T，那么有：

由全局分歧定理［12］知，定理1中的局部分歧正解Γ＊可以延拓为全局分歧，令M为Γ＊沿a方向的极大连通分支，则M 为问题（9）式由（a＊；θa＊，0）出发的解曲线，令P＝P1×P2，其中P1＝｝，易得在（a＊；θa＊，0）的小邻域内，M⊂P。由全局分歧定理得 M－｛（a＊；θa＊，0）｝满足下列条件之一：

（1）M 连接到（a1；0，0）。

（3）M 连接到（a2；0，θb）。

（4）M 在R＋×P内由（a＊；θa＊，0）延伸到∞。

条件（1）显然不成立，假设条件（2）成立，则存在序列｛（an；Un，Vn）｝⊂M，使得n→∞，an→，（Un，Vn）在［L∞（Ω）］2中收敛到（θ，0）。由（un，vn）和（Un，Vn）之间存在一一对应关系知，（un，vn）→（θ，0），令，则满足方程：n

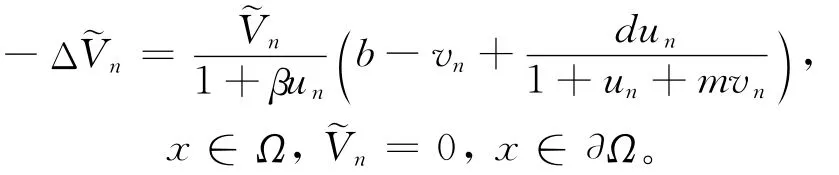
由Sobolev嵌入定理和Lp估计知，（在C1范数意义下），且满足：

接着证明当a充分大时条件（3）也不成立。反证，假设存在序列αn→∞，an→a2，（Un，Vn）在［L∞（Ω）］2中收敛到（0，θb），由（un，vn）和（Un，Vn）之间存在一一对应关系知（un，vn）→（0，θb）。令，则n满足方程：

由Sobolev嵌入定理和Lp估计知（在C1范数意义下），且满足：－Δ＝0，x∈Ω，＝0，x∈∂Ω，所以＝0，与‖‖∞＝1矛盾。

由以上讨论可知条件（4）成立，即有M－｛（a＊；θa＊，0）｝⊆P，因为‖U‖∞、‖V‖∞有界，全局分歧曲线只能随参数a到无穷。

同理可得定理4。

定理4 定理2中的局部分歧正解Γ＊可以延拓为全局分歧，且存在常数充分大，使得当β≥时，全局分歧曲线随参数a到无穷。

注意到（u，v）≥0和（U，V）≥0之间存在一一对应关系，由定理3、定理4知，当a＞a＊（b）或a＞a＊（b）时，模型（5）式存在分歧正解。

［1］ 柴俊平，李艳玲.带有交叉扩散项的捕食－食饵模型的全局分歧［J］.纺织高校基础科学学报，2011，24（4）：489－494.

［2］ 何其慧.捕食者具有阶段结构的食饵－捕食系统的研究［J］.合肥工业大学学报：自然科学版，2009，32（4）：546－549.

［3］ Hwang T W.Global analysis of the predator－prey system with Beddington－DeAngelis functional response［J］.J Math Anal Appl，2002，281：395－401.

［4］ 马晓丽.一类具有交叉扩散的捕食模型的整体分歧［J］.西安工业大学学报：自然科学版，2010，30（5）：506－510.

［5］ Beddington J R.Mutual interference between parasites or predators and its effect on searching efficiency［J］.J Animal Ecol，1975，44（1）：331－340.

［6］ DeAngelis D L，Goldstein R A，O’neill R V.A model for trophic interaction［J］.Ecology，1975，56（2）：881－892.

［7］ 郭改慧，吴建华，一类捕食－食饵模型正解的存在性与惟一性［J］.武汉大学学报；理学版，2008，54（1）：9－14.

［8］ 叶其孝，李正元，王明新，等.反应扩散方程引论［M］.北京：科学出版社，2011：40－56.

［9］ Crandall M G，Rabinowitz P H.Bifurcation from simple eigenvalues［J］.J Functional Analysis，1971，8（2）：321－340.

［10］ Rabinowitz P H.Some global results for nonlinear eigenvalue problems［J］.J Functional Analysis，1971，7（3）：487－513.

［11］ Wu J H.Global bifurcation of coexistence state for the competition model in the chemostat［J］.Nonlinear Analysis，2000，39（7）：817－835.

［12］ Smoller J.Shock waves and reaction－diffusion equations［M］.New York：Springer－Verlag，1999：167－180.