具有通信时延的多个体网络量化一致性分析

张丹丹

（南昌航空大学 信息工程学院，江西 南昌 330063）

0 引 言

多个体网络由大量个体或节点相互信息交互耦合而成，每个个体仅能与其周围邻居个体进行信息传递。由于不需要网络全局信息，多个体网络在复杂环境下具有极强的鲁棒性和适应能力，以及节约成本等优点，因而在过去十多年中，多个体网络的相关研究引起了不同领域学者们的广泛关注。作为多个体网络最根本的问题，一致性问题的研究更是受到极大关注，并取得了丰硕成果。在多个体网络中，一致性是指在没有中央集总控制情况下，个体间仅通过局部的交互作用使所有个体状态趋于相同［1－2］，并在多移动机器人编队控制［3－4］、卫 星 姿 态 同 步［5］等 方 面 具 有 广 泛 应用。一致性问题的关键在于设计合理的一致性协议，使网络中的个体能够就感兴趣的状态变量达成共识。而作为一致性问题的特例，平均一致性问题则要求最终的一致性值为网络中所有个体初始状态的算术平均。

随着计算机技术、网络技术和通信技术的进一步发展，多个体网络应用更加广泛，并涌现出一大批新的更加复杂的应用需求。由于实际通信网络的数字通道带宽有限，从而导致网络中个体的状态信息在发送给其邻居个体之前必须进行量化，个体间只能基于量化状态信息而非精确状态信息进行通信。因而设计有效的量化一致性协议，使得多个体网络基于量化信息通信涌现出期望的群体动力学行为，成为近年来多个体网络研究的一个新热点课题［6－13］。

常用量化策略主要有均匀量化和对数量化2类。文献［6］研究了固定拓扑无向网络的量化一致性问题，得到了网络达到平均一致性时量化器参数与无向网络拓扑结构参数间的定量关系。文献［7］通过设计合适的均匀量化策略，固定拓扑无向网络中的任意邻居个体仅需互惠地发送有限比特量化信息，就足以确保网络达成平均一致性。但无向网络要求个体之间必须进行双向信息传递，而不同个体具有不同的信息传输能力，因此实际网络一般都是有向的。因此，基于对数量化策略，文献［12］研究了有向平衡网络的量化一致性问题，并发现在所提出的量化一致性协议作用下，所有个体能达成β－平均一致性，即当对数量化器扇形边界参数β趋于0时，网络中个体渐近地达成平均一致性。但平衡网络意味着所有个体在网络中具有同等重要性［2］，这一要求在实际应用中过于苛刻。因此，基于均匀量化策略，文献［9］研究了固定拓扑有向非平衡网络的量化一致性问题，所提出的量化一致性协议允许个体之间可以进行单向、非平衡的信息通信。此外，由于一个个体可以进入或离开其他个体的有效感知范围，这意味着在通信图中，某些边被移去或加入了新的边，从而导致切换拓扑［1－2］。采用自适应均匀量化策略，文献［8，10］分别研究了无向切换网络和有向切换网络的量化一致性问题。

当个体间进行信息交换时，信息传输速度通常受到实际通信设备物理性能的限制，这使得发送方的信息会经过一定时间延迟后才能被接收方收到，从而导致通信时延的产生。因此，研究量化和通信时延共存情形的多个体网络一致性问题既有极强的实际应用背景，也是非常有必要的。文献［11］在文献［7］的基础上，采用均匀量化策略研究发现只要无向网络中个体间的通信时延有上界，则所有个体仍能达成平均一致性。但文献［11］仅研究了无向网络情形，从而限制了其应用范围。

本文在文献［9，12］的基础上，采用对数量化策略研究了量化和时延共存情形下的固定拓扑有向非平衡多个体网络的一致性问题。结果表明，无论对数量化信息多么粗糙，只要选取合适的增益参数，则所提出的量化一致性协议是可接受的，且多个体网络以指数速度达成β－加权平均一致性。此外，本文揭示了一致性误差的上界对对数量化器扇形边界参数β的依赖关系，并用仿真实例验证了本文理论分析的有效性。本文通过引入时延节点将系统扩维，将存在通信时延的量化一致性问题转化为无时延的量化一致性问题，并利用相关强非周期马尔科夫（Markov）链的收敛结论［14］进行一致性分析，而文献［11］主要运用无向图的代数图谱理论和对称矩阵分解方法来分析一致性，该方法不适用于本文所考虑的有向网络。

1 准备知识

1.1 图论基础知识

多个体网络的通信拓扑通常可以建模成有向图G＝（V，ε，W），其中，网络中个体或节点集V＝｛1，2，…，N｝，N 为个体数目；边集ε＝｛eij＝（i，j）｜i，j∈V｝；与有向网络相对应的邻接矩阵W＝（wij）∈RN×N，有向边eji∈ε表示个体j向个体i发送信息，这时个体j称为个体i的入度邻居，此时的有向边（j，i）对应的边权wij＞0，否则wij＝0。若有向图G中的有序节点序列（i1，i2，…，ir）满足eij，ij＋1∈ε，j∈｛1，…，r－1｝，则称该有序节点序列为有向图G中的一条有向路径。如果有向图G中的任意2个不同节点i和j之间都存在一条有向路径，则称图G是强连通的。由于每个个体可获悉自身状态信息，本文假定所有个体具有自环或eii∈ε（i∈V）。如果图G中任意节点i的入度和出度都相等，即对任意i∈V，成立，则称图G为平衡图。若W 中的任意元素wij≥0且满足W1＝1，1＝（1，1，…，1）T，则W 称为 （行）随 机 矩 阵。进 一 步 地，若1TW＝1T还成立，则W 称为双随机矩阵，此时网络对应的有向图为平衡图［2］。

1.2 对数量化器

对数量化器可以用非线性函数q（·）：R→Γβ来表示，其作用是将实数集R映射到离散量化水平集Γβ，并定义为：对任意实数m，有

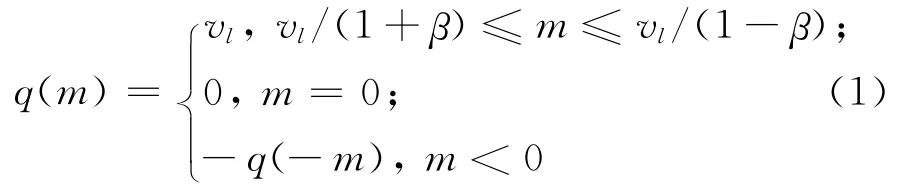
对应的离散量化水平集Γβ为：

Γβ＝ ｛±vl｜vl＝ρlv0，l＝±1，±2，…｝∪ ｛0｝。其中，v0＞0为已知常数；0＜ρ＜1为对数量化器的密度参数；待设计参数β＝（1－ρ）／（1＋ρ）∈（0，1）表示对数量化器的扇形边界参数［12］，即对数量化器满足：

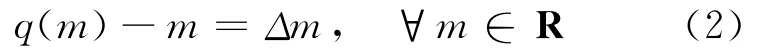
其中，Δ∈［－β，β］为因对数量化所导致的误差。（2）式表明β越大，量化信息越不精确或越粗糙；相反地，β越小则量化信息越接近真实信息。

2 问题描述

考虑具有N个个体的多个体网络，其中个体i∈V具有离散一阶动力学［6－11］如下：

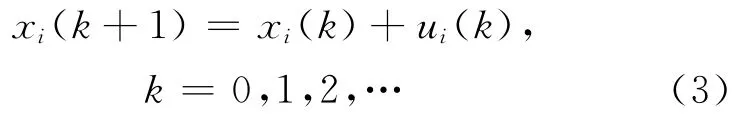
其中，xi（k）为个体i在k时刻的状态；ui（k）为个体i的控制输入或协议。

由于个体间信息交换受有限带宽限制以及通信时延的影响，实际上个体i接收到个体j的信息为：

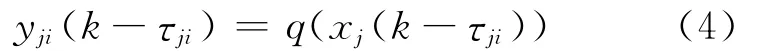
其中，q（xj（k－τji））为个体i在第k时刻接收到个体j在k－τji时刻的量化状态；τji为有向边eji的通信时延。

则由（2）式得：

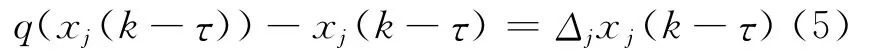
其中，Δj∈［－β，β］；∀j∈V。

对网络拓扑和时延作假设1、假设2。

假设1 有向强连通图G对应的随机邻接矩阵W具有正对角元，即存在一个正数w满足；同时wij∈｛0｝∪［w，1］对任意i≠j成立。

假设2τii＝0对任意i∈V成立；当wij＝0时，τji＝0；存在一个有限正常数B，对任意i，j∈V满足0≤τji≤B，即通信时延一致有上界。

对个体i∈V在第k时刻设计的一致性协议如下：

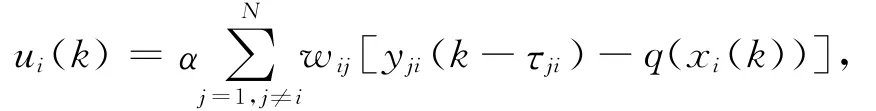
其中，α∈（0，1］为待定的增益参数；wij为随机邻接矩阵W对应位置的元素。由（1）式、（5）式可知，（6）式表明个体i利用了其邻居个体和自身的量化状态信息，因而（6）式由β确定。

利用（4）式，并把（6）式代入（3）式得：

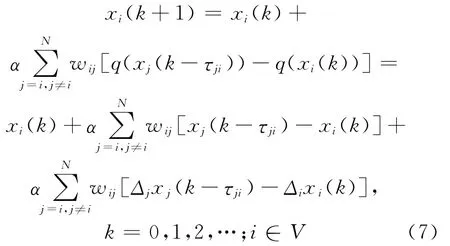
3 系统扩维

若信息由个体j发出后经过τji步延迟后到达节点i，则可以通过在网络图G中节点j和节

点i之间增加τji个时延节点来描述时延，而在没有发生通信时延的节点之间则无需增加时延节点，则整个网络添加的时延节点总数为。 为 叙 述 方 便，本 文 令xN＋1（k），…，xb（k）为时延节点状态，通过例子说明系统扩维的过程。

例1 设有一个3个节点的有向强连通图G，如图1a所示。设节点3和节点1间的时延为2，其他节点之间无时延，如图1b所示。

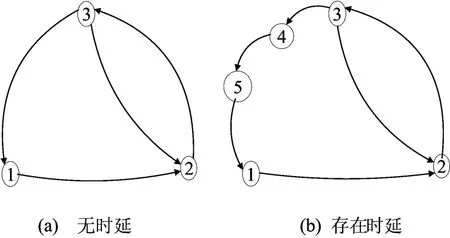
图1 无时延和存在时延时的网络图

设图1a无时延情况时的随机矩阵W为：

其各行的行和均为1。

图1b中，因为节点3、1间的通信时延为2，故在有向边e31插入时延节点和5，这样节点3首先发送信息至第1个时延节点4，权为34＝1，节点4发送信息给节点5，权为54＝1，再经由节点5发送信息至节点1，权为15＝2／3。从而得到时延情形下的有向图所对应的邻接矩阵＝j）为：仍为一个随机矩阵。

由于时延节点仅传递信息而没有自环，故引入时延节点后的有向图所对应的邻接矩阵所有主对角元素ii不全为正数，表明对应一个不可逆Markov链，且该Markov链不是强非周期的［12］。因此，目前文献中许多关于强非周期Markov链的收敛结论对本文不再适用。此外，由于不是对称矩阵，则文献［9］中对称矩阵分解方法对本文不再适用。令

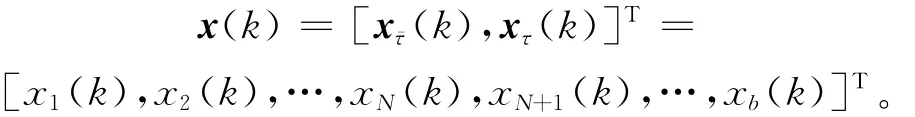
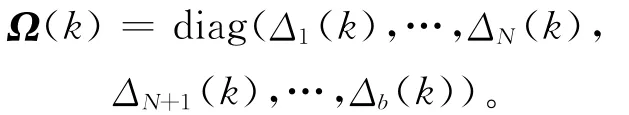
其中，ΔN＋1（k），…，Δb（k）表示时延节点所对应的量化不确定性，且满足：

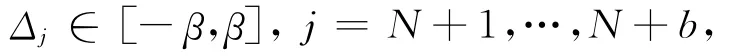
则通过系统扩维引入时延节点后，（7）式可写成为：

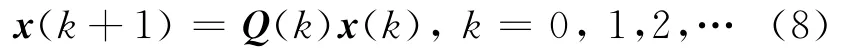
其中，迭代矩阵为：

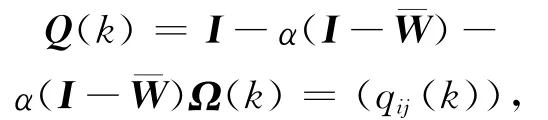
其中，I为适当维数的单位矩阵。

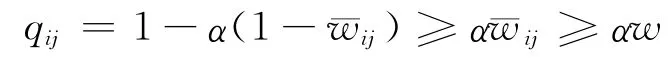
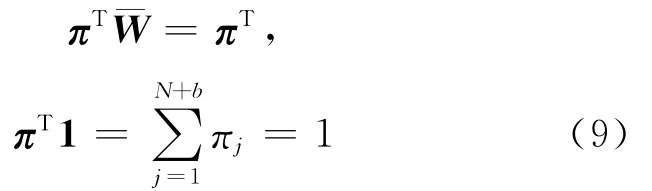
其中，1＝（1，1，…，1）T，同时成立。

根据（9）式，对迭代矩阵Q（k），πTQ（k）＝πT也成立，亦即Q（k）和具有相同的平稳分布。因而由（8）式可得：

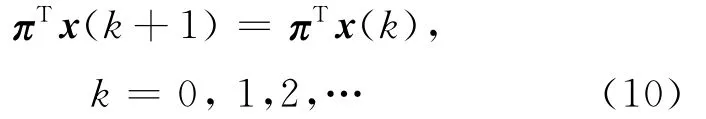
这意味着在有界时延和量化信息通信情形下，多个体网络仍保持加权平均一致性不变性［9］，当π1＝π2＝…＝πN＋b＝1／（N＋b）时，网络中所有个体具有同等重要性［2］，即退化为平均一致性情形。

令一致性误差为δ（k）＝（I－J）x（k），其中J＝1πT。则由（10）式得：

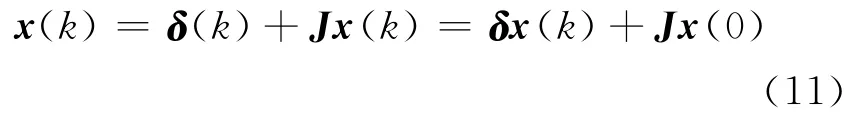
将（11）式带入（8）式，并利用（9）式可得一致性误差方程为：

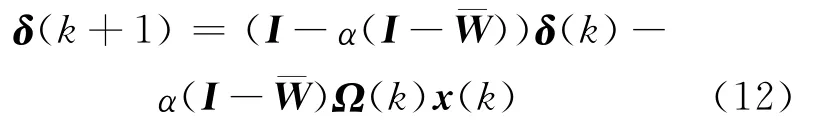
定义1 设个体间基于对数量化信息通信，若对任意β∈（0，1），在一致性协议作用下有：

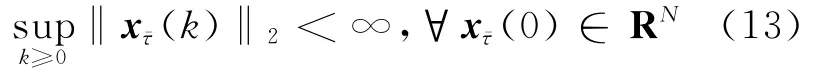
其中，sup表示上确界，则称一致性协议为可接受的。进一步地，在可接受一致性协议作用下，若有：

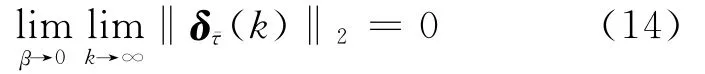
则称多个体网络达成β－加权平均一致性。当扇形边界参数β渐近地趋于0时，非时延节点一致性误差δ（k）也渐近趋于0。

本文采用对数量化策略，并给出适当的扇形边界参数β设计准则，使得在有界时延与对数量化信息通信情形下，所提出的一致性协议能确保多个体网络达成β－加权平均一致性。

4 一致性分析

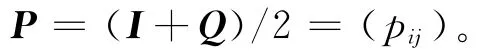
随机矩阵P描述了一个强非周期Markov链，进一步地，定义加性随机矩阵［14］为：

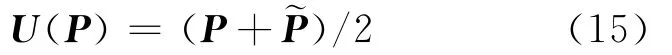
引理1 随机矩阵Q描述了一个Markov链［14］，且具有平稳分布π，即，并有：

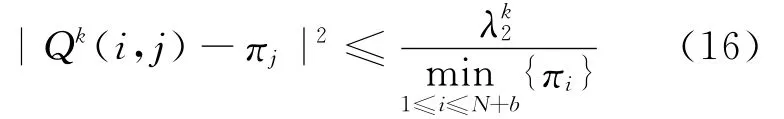
其中，Qk（i，j）为矩阵Qk第i行第j列位置的元素；1＞λ2＝λ2（U（P））＞0为矩阵U（P）的第二大特征值；πj为满足（9）式的向量π的第j个分量。

定理1 设假设1、假设2成立，对任意β∈（0，1），若选取，则一致性协议（6）式是可接受的，且有：

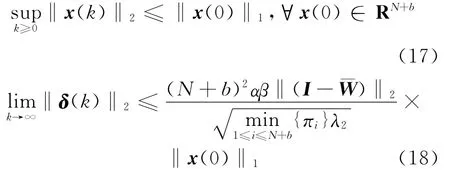
再根据δ（k）定义，由（18）式可得（12）式，即多个体网络达成β－加权平均一致性。

证明 对任意β∈（0，1），由于｜Δj（k）｜≤β＜1及0＜α≤1／（1＋β）＜1，因此有‖α（I＋Ω（k））‖2≤1，则QT（k）＝I－α（I＋Ω（k））（I－）T是一个列随机矩阵（每列的和均为1），且与属于相同的类［15］，并有：

‖Q（k）‖1＝ ‖QT（k）‖∞＝1。

则由（8）式可得：

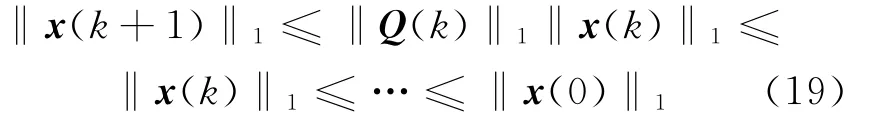
对向量x（k），‖x（k）‖2≤‖x（k）‖1成立，因而（17）式成立。进一步地，由于x（k）＝［x（k），xτ（k）］T，故‖x（k）‖2≤‖x（k）‖2，则由（17）式可得（13）式，即一致性协议是可接受的。

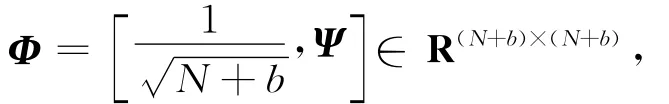
其中，Ψ∈R（N＋b）×（N＋b－1）满足ΨT1＝0，并有：

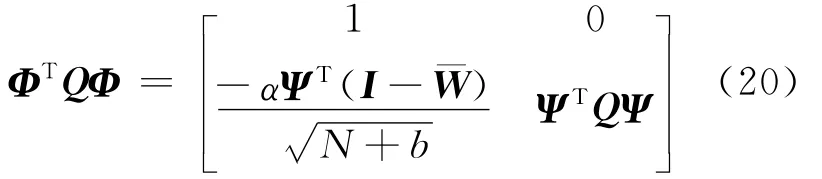
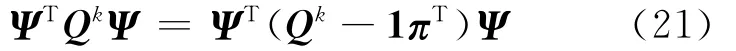
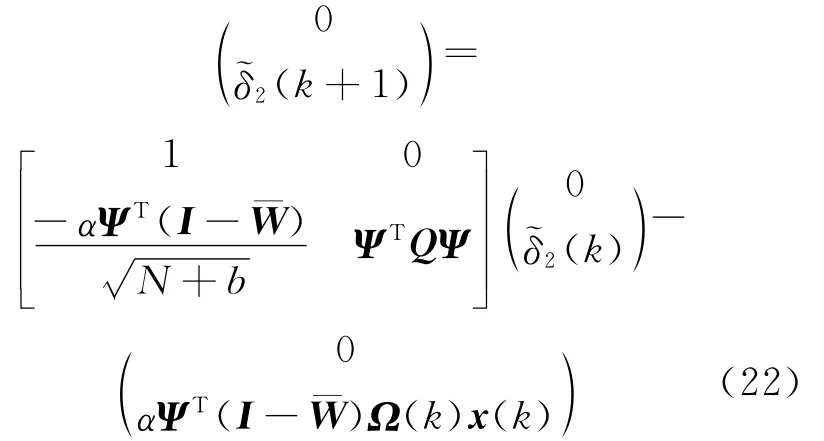
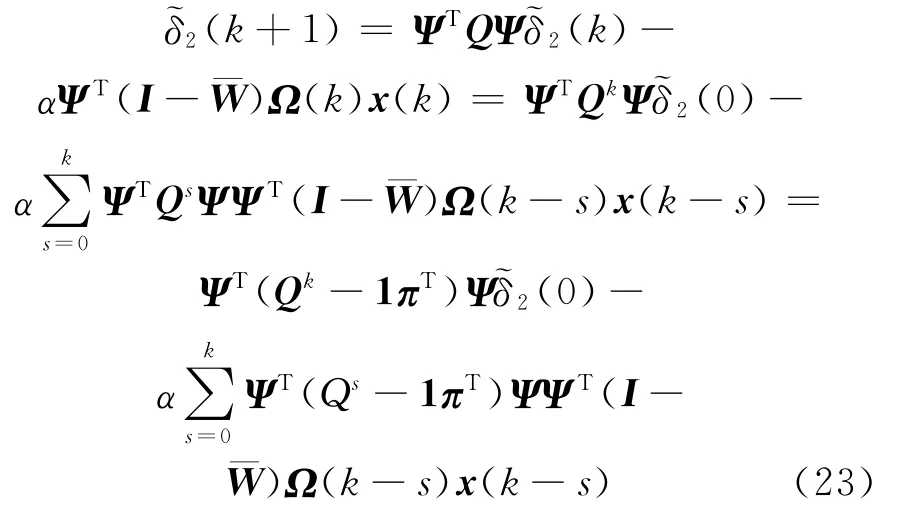
根据范数性质和Φ定义，由（16）式和（21）式可得：

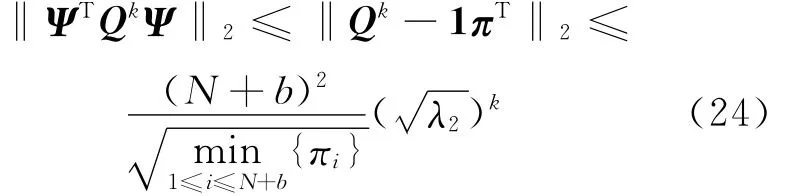
进一步地，由于‖Ω（k－s）‖2≤β，则由（17）式、（23）式和（24）式可得：

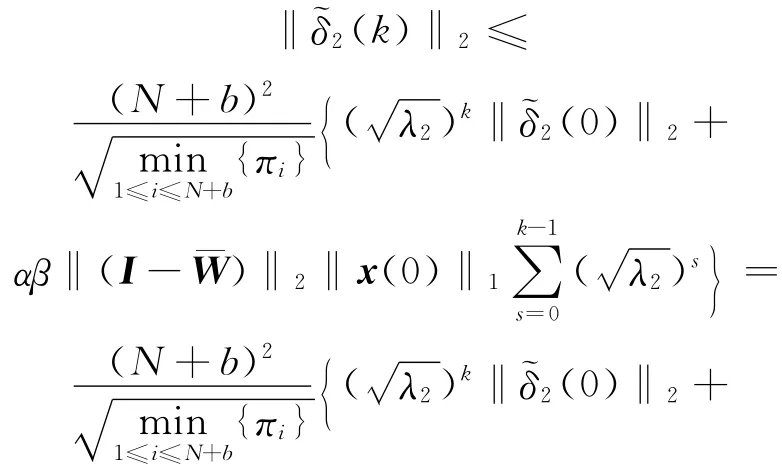
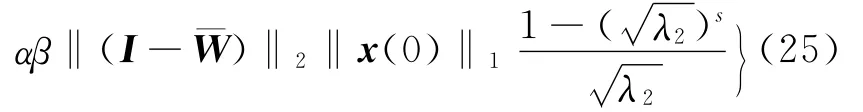
对任意k≥0，‖~δ2（k）‖2＝‖δ（k）‖2成立，当1＞λ2＞0时，则由（25）式可得（18）式。

定理1表明，只要强连通有向网络中的通信时延有上界，则对任意β∈（0，1），只要选取α∈（0，1／（1＋β）］，多个体网络最终依指数速度达成β－加权平均一致性，最终所有个体状态趋于πTx（0）的邻域内。且（18）式表明，引入非线性对数量化过程，一致性误差上界依赖于个体数目、通信时延、对数量化器扇形边界参数β和个体初始状态值。因此，定理1将无通信时延有向平衡网络、个体动力学为连续与采样一阶情形的量化一致性相关结论［12］推广到存在通信时延有向非平衡网络、个体动力学为离散一阶情形。

5 数值仿真

考虑如图1a所示的3个个体有向图G，个体状态初始值x0＝ （－ 2.45 1.57 2.02 ）T，并设除自环外的通信时延τji均为1，且引入的时延个体初始状态均设为0，则计算可得基于精确信息通信的多个体网络一致性值为：

x＊＝ （0. 850 2 0.850 2 0.850 2 ）T。仿真中对数量化器参数v0取2。

首先令β＝0.8∈（0，1），则按照定理1，取α＝0.5∈（0，1／（1＋β）］，迭代40次后的个体状态轨迹图如图2所示。

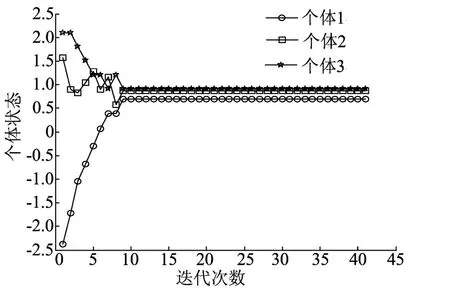
图2 β＝0.8，α＝0.5时3个个体状态轨迹

令β＝0.08，取α＝0.5，可得迭代40次后的个体状态轨迹图如图3所示。

图2和图3表明，只要强连通网络中的通信时延有上界，基于任意粗糙量化信息通信的多个体网络总可以指数地达成β－加权平均一致性；且对数量化信息越精确，即β越小，则个体状态越趋近于无量化信息通信时的一致性值x＊。

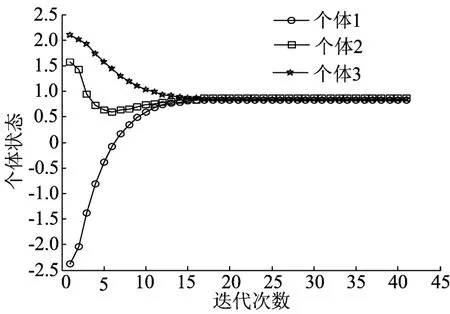
图3 β＝0.08，α＝0.5时3个个体状态轨迹

6 结束语

针对通信时延有界的固定拓扑有向强连通非平衡网络，本文基于对数量化策略提出一种量化一致性协议。进一步利用相关强非周期Markov链的收敛结论，证明所提出的量化一致性协议是可接受的，且无论对数量化信息多么粗糙，只要选取合适的增益参数，多个体网络最终以指数速度达成β－加权平均一致性。此外，解析地揭示了一致性误差的上界对对数量化器扇形边界参数β的依赖关系，并用仿真例子验证了本文理论分析的有效性。作为后续研究，本文将采用对数量化策略，进一步考虑具有时变通信时延的有向切换网络量化一致性问题。同时，将本文网络拓扑的强连通条件弱化为生成树条件，也将是有待解决的问题之一。

［1］ Jadbabaie A，Lin J，Morse A S.Coordination of groups of mobile autonomous agents using nearest neighbor rules［J］.IEEE Transactions on Automatic Control，2003，48（6）：988－1001.

［2］ Olfati－Saber R，Murray R M.Consensus problems in networks of agents with switching topology and time－delays［J］.IEEE Transactions on Automatic Control，2004，49（9）：1520－1533.

［3］ Ou M Y，Du H B，Li S H.Finite－time formation control of multiple nonholonomic mobile robots ［J］.International Journal of Robust and Nonlinear Control，2014，24（1）：140－165.

［4］ 蒋建国，夏 娜.基于MAS的分布式智能控制初探［J］.合肥工业大学学报：自然科学版，2005，28（9）：1085－1088.

［5］ Du H B，Li S H，Qian C J.Finite－time attitude tracking control of spacecraft with application to attitude synchronization［J］.IEEE Transactions on Automatic Control，2011，56（11）：2711－2717.

［6］ Carli R，Bullo F，Zampieri S.Quantized average consensus via dynamic coding／decoding schemes［J］.International Journal of Robust and Nonlinear Control，2010，20（2）：156－175.

［7］ Li T，Fu M Y，Xie L H，et al.Distributed consensus with limited communication data rate［J］.IEEE Transactions on Automatic Control，2011，56（2）：279－292.

［8］ Li T，Xie L H.Distributed consensus over digital networks with limited bandwidth and time－varying topologies［J］.Automatica，2011，47 （9）：2006－2015.

［9］ Li D Q，Liu Q P，Wang X F，et al.Consensus seeking over directed networks with limited information communication［J］.Automatica，2013，49（2）：610－618.

［10］ Li D Q，Liu Q P，Wang X F，et al.Quantized consensus over directed networks with switching topologies［J］.System and Control Letters，2014，65：13－22.

［11］ Liu S，Li T，Xie L H.Distributed consensus for multi－agent systems with communication delays and limited data rate［J］.SIAM Journal on Control and Optimization，2011，49（6）：2239－2262.

［12］ Liu S，Li T，Xie L H，et al.Continuous－time and sampleddata based average consensus with logarithmic quantizers［J］.Automatica，2013，49（11）：3329－3336.

［13］ 李 韬，孟 扬，张纪峰.多自主体量化趋同与有限数据率趋同综述［J］.自动化学报，2013，39（11）：1805－1811.

［14］ Fill J A.Eigenvalue bounds on convergence to stationarity for non－reversible Markov chains，with an application to the exclusion process［J］.The Annals of Applied Probability，1991，1（1）：62－87.

［15］ Wolfowitz J.Products of indecomposable，aperiodic，stochastic matrices［J］.Proceedings of the American Mathematical Society，1963，14（5）：733－737.

［16］ Horn R A，Johnson C R.Matrix analysis［M］.Cambridge：Cambridge University Press，1985：33－57.