面向车间生产性能诊断的改进TOPSIS评价方法

徐文杰， 綦法群

（1.中国电子科技集团公司第三十八研究所，安徽 合肥 230088；2.同济大学 工业工程研究所，上海 200092）

0 引 言

工业工程师作为“企业医生”，首要任务便是诊断出管理对象的“健康状况”，进而才能确定采取何种工业工程技术进行能力提升和问题改善。车间生产性能评价的目的在于确定车间在各个指标性能上与比较对象的差距，然后诊断出其薄弱环节，指导生产性能的提升。关于车间制造系统的性能研究，得到了很多学者的关注。文献［1］应用仿真方法来评价不同制造系统的性能，选取的评价指标包括制造提前期、提前期偏差、利用率和在制品数量；文献［2］建立了3层多属性价值的安全管理评价模型，共101个因素，并通过计算喷涂车间的安全指标来评价生产管理的安全状况；文献［3］针对半导体封装测试生产线，从生产能力CT、TH、WIP等性能评价指标对半导体封装测生产线的生产性能进行了研究；文献［4］研究了精益生产中财务指标对其生产性能的影响，特别是对于库存的影响作用；文献［5］使用组合赋权评价方法研究了对装配人员的优化；文献［6］应用改进模糊层次分析法对工程的风险进行评估。然而，目前的研究忽视了如何诊断问题，过多的是根据研究者的偏好假设车间存在某方面问题，然后考虑如何改善。

本文研究的重点是解决如何全面诊断，通过综合评价方法来发现车间生产性能的优劣，进而针对性地改善。

1 基于改进TOPSIS的评价方法

1.1 方法介绍

TOPSIS评价方法通过构造最优解和最劣解空间，将评价对象看作是空间中的一点，根据该点在最优解和最劣解之间的位置，来判定评价对象性能的相对优劣情况［7］。基于灰色关联度分析的改进TOPSIS的评价方法，在灰色关联度评价模型基础上，根据TOPSIS评价思想对参考数列进行修正。灰色关联度评价模型中参考数列是由每一个指标最优值构成的，相当于TOPSIS方法中的最优解。因此，可以将灰色关联度［8］的最终结果看作是评价对象与最优解的绝对接近程度。虽然该方法可以评价出对象的优劣，但其对于对象间的差距描述不够合理。

相对与绝对接近程度比较如图1所示。

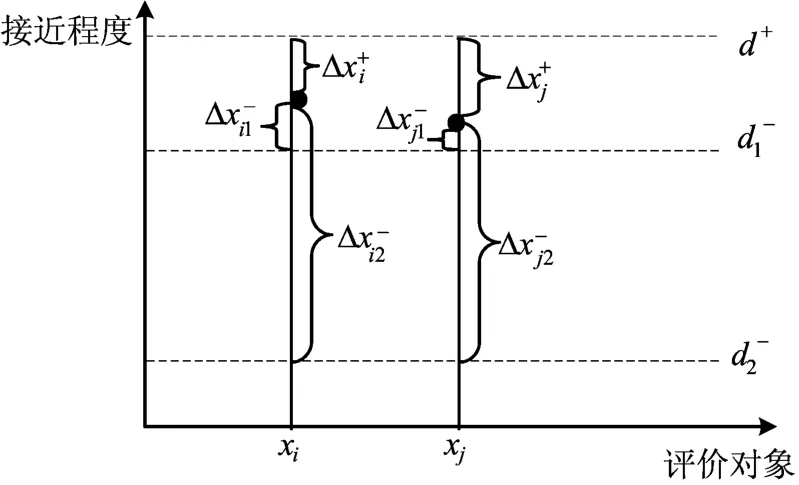
图1 相对与绝对接近程度比较

图1中，xi与xj为2个评价对象，其评价值分别为ei和ej；d＋为最优解为2组最劣解；分别为xi与xj的评价值与d＋的接近程度；分别为xi与xj的评价值与d－1的接近程度为xi与xj的评价值与d－2的接近程度。灰色关联度评价对于xi与xj的评价是通过的值的大小，其只考虑评价对象与最优解之间的距离。然而，对于不同的最劣解情况2个评价对象接近最优解的情况是不同的。对于，xj距离d＋距离更远，其更接近于，反映为该评价对象表现比较差；而对于与d＋的距离就相对比较近，说明评价对象表现较好。在实际生产性能的评价中，不仅仅需要评价对象的排序，往往还需要清楚评价对象在行业内的位置和性能等级。相同的，灰色关联度评价得到了不同的解释，说明灰色关联度评价不能够用于评价对象的分级定位。

基于灰色关联度分析的改进TOPSIS的评价模型将分别选取2组参考数列进行灰色关联度计算。原灰色关联度评价中的参考数列作为TOPSIS的最优解，另外选取一组各指标的实际最劣值作为参考数列为最劣解，然后根据TOPSIS方法计算评价值与最优解的相对接近程度，其评价过程如图2所示。

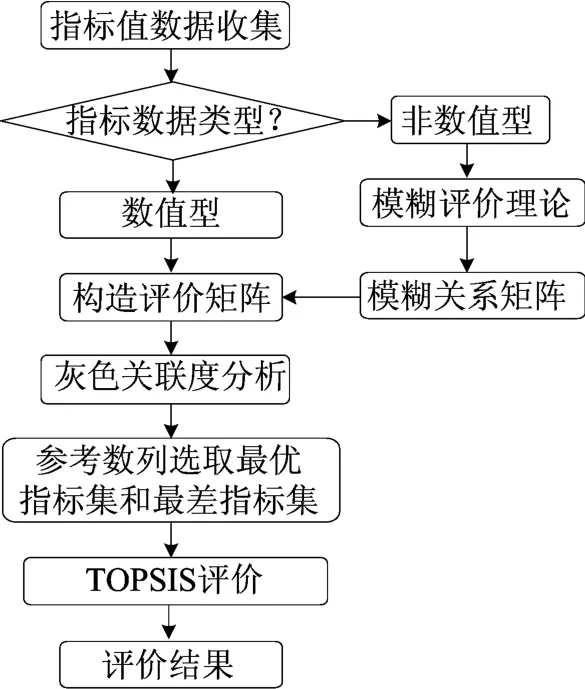
图2 改进TOPSIS的评价过程

1.2 评价步骤

（1）构造评价矩阵。设有m个评价单元U＝｛u1，u2，…，um｝，对任一评价单元通过n个属性进行评价，评价指标构成矩阵为：

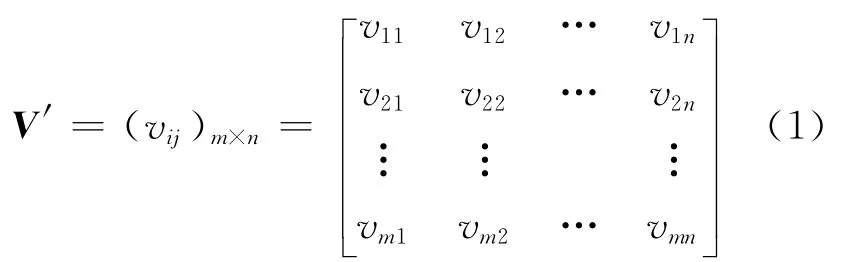
（2）参考数列的选取。对于（1）式所示的评价矩阵V′，选取参考数列和）作为最优解和最劣解，其中

（3）指标值规范化处理。评价矩阵采用极差无量纲法规范化处理后按照（2）式、（3）式所示重新选取参考数列，得到结果如下：

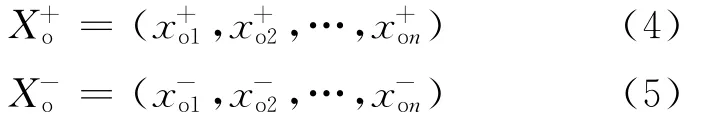
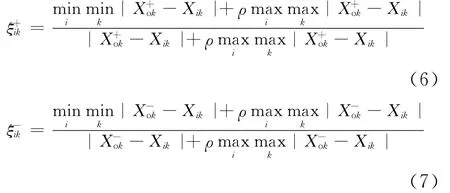
计算各评价对象的评价指标值与最优解和最劣解的关联系数，得到关联系数矩阵如下：

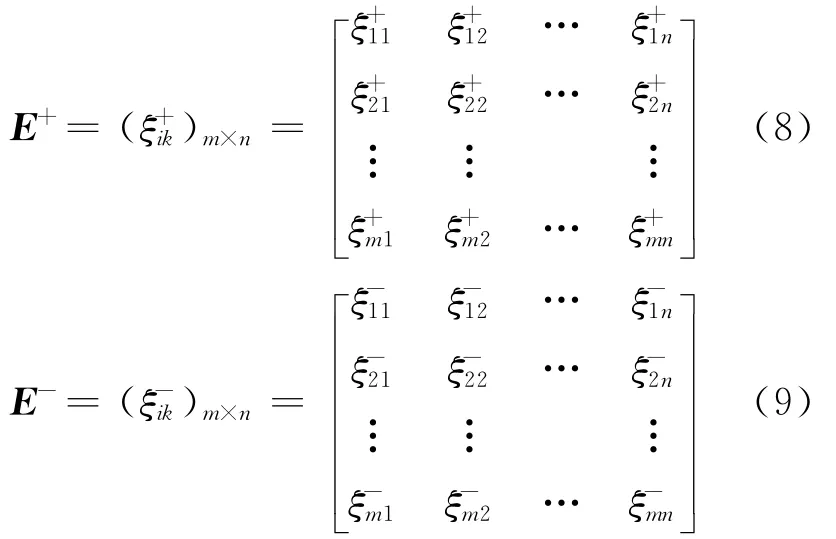
（5）计算最终关联度。分别用E＋、E－2个关联系数矩阵计算单层和多层次关联度，则最终关联度为：

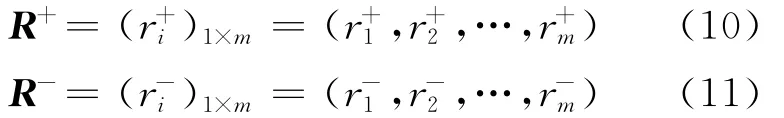
（6）计算与最优解的相对接近度。

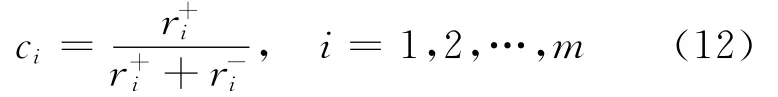
最终得到的接近度集合为：

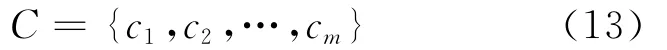
（7）排序。依据对最优解的接近度ci大小进行评价单元排序。接近度越大，表明该评价单元与最优解越接近。

2 实例分析

本文以生产某电子装备制造企业的5个生产车间（P1，P2，P3，P4，P5）为研究对象，评价各车间的综合生产性能。通过实地调研，选取了对于企业比较关键的6个一级指标进行评价，各一级指标所对应的二级指标见表1所列。

（1）评价数据。5个生产车间的各指标数据Vik（i＝1，2，…，m；k＝1，2，…，n）见表2所列，其中指标特征为“1”表示该指标值的关联度取大为优，“0”则表示取小为优。

为更准确地客观反映制造企业的车间生产性能，评价体系构建之初尽量选用可定量分析的指标。但是，对于B41指标（产品创新系数）来说，很难用具体数字表示，该指标值一般用语义描述，数据收集时根据语言变量LV＝（非常不满意，不满意，稍微满意，满意，非常满意），分别赋值X＝（1，2，3，4，5），然后进行指标无量纲处理。

表1 生产性能评价指标体系

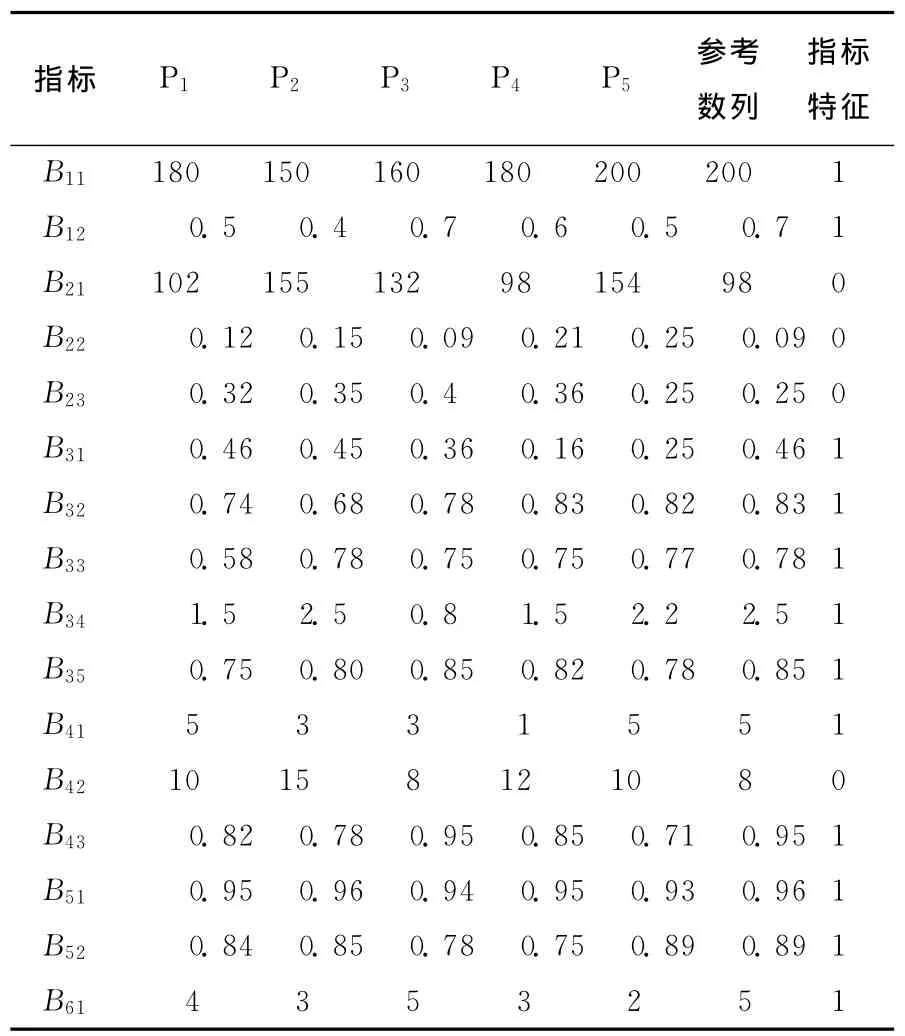
表2 5个生产车间指标数据表

（2）计算单层关联度。计算各评价对象的指标数据与最优解的关联系数，所得数值见表3所列。

表3 指标数据与最优解的单层关联度系数

计算各评价对象的指标数据与最劣解的关联系数，结果见表4所列。

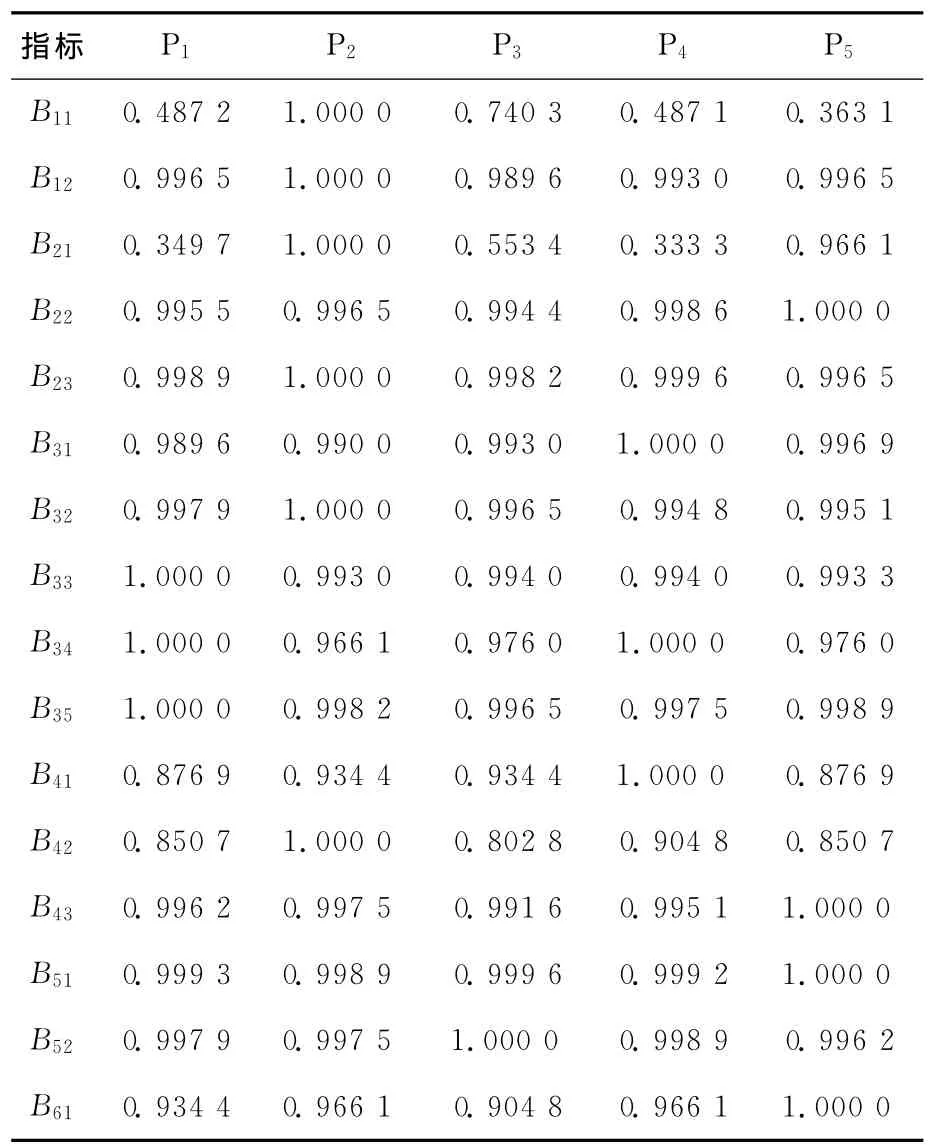
表4 指标数据与最劣解的单层关联度系数

（3）计算多层评价系统的最终关联度。利用（10）式和（11）式分别计算各评价对象与最优解和最劣解之间的关联度：

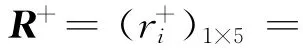
（0.943 5，0.883 9，0.919 1，0.933 7，0.954 1）；（0.898 6，0.990 8，0.923 1，0.911 8，0.918 8）。

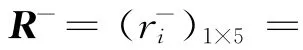
图3所示为基于TOPSIS的改进灰色关联度分析结果。

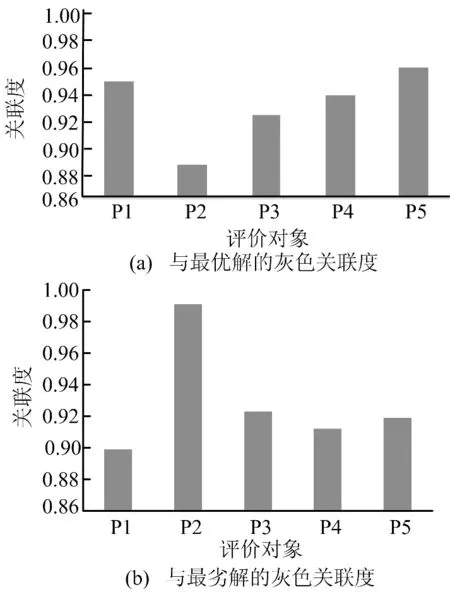
图3 基于改进TOPSIS的评价分析结果

（4）车间生产性能排序。根据（12）式得到评价对象与最优解的相对接近度：C＝（0.512 2，0.471 5，0.498 9，0.506 0，0.509 4）。

根据接近度大小，可以得到车间生产性能的优劣次序为：P1≻P5≻P4≻P3≻P2。

（5）评价结果分析。改进TOPSIS与灰色关联度方法的结果比较，见表5所列。

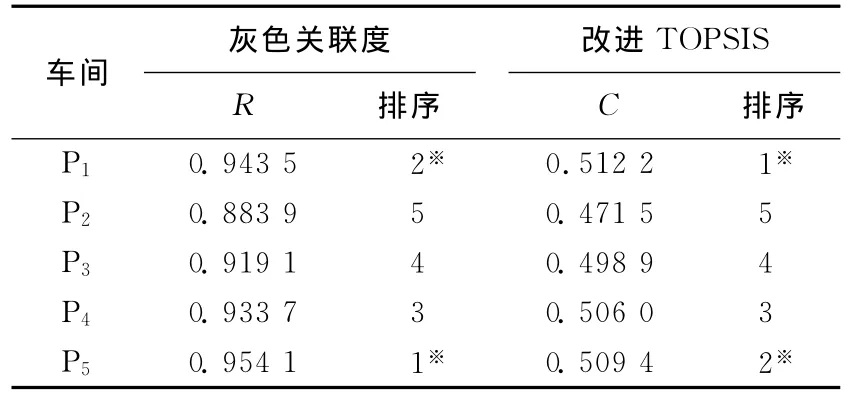
表5 不同评价方法结果比较

其中，传统灰色关联度分析结果与基于灰色关联度分析的改进TOPSIS的评价方法存在差异，排名第1和第2的2个车间性能的评价结果不同。这是由于传统模糊灰色关联度分析得到的是评价对象与最优解之间的绝对接近程度，而忽视了其解在最优解与最劣解之间的位置，导致了衡量评价对象时不能够准确对其定位。

在图3a中比较P1与P5，可知P5与最优解的灰色关联度值最大，这也是传统模糊灰色关联度分析得到的结果。然而从图3b可知，P5与最劣解的灰色关联度值并不是最小，P1与P4与最劣解的灰色关联度值都小于它，其中P1为最小值。这说明传统灰色关联度忽视了与最劣解的关联情况。通过基于灰色关联度分析的改进TOPSIS的评价方法进行分析，可以得到更加客观准确的值。

3 结束语

基于灰色关联度的改进TOPSIS方法为传统TOPSIS评价提供了更为具有实际参考价值的最优解与最劣解。通过分别计算评价值与最优解和最劣解的关联度，构建相对接近度来反映评价对象的指标在最优解和最劣解空间的分布位置，克服了灰色关联度只考虑与最优解接近程度而忽视了评价指标的综合性能的不足，能够更加客观地反映评价对象与竞争对象的关系。通过改进TOPSIS方法评价，可以为车间生产性能诊断提供数据支撑，更加客观地反映车间生产性能的相对优劣，诊断出急切需要进行改善的对象及其需要改善的具体指标，有利于后期采用针对性的工业工程方法进行改善，减少由于诊断问题不清而导致的多余和不当的改进工作造成的浪费。

［1］ Koruca H I，Ozdemir G，Aydemir E，et al.The simula－tion－based performance measurement in an evaluation module for Faborg－Sim simulation software［J］.Expert Systems with Applications，2010，37（12）：8211－8220.

［2］ James I，Liang C L.Performance evaluation of process safety management systems of paint manufacturing facilities［J］.Journal of Loss Prevention in the Process Industries，2009，22（4）：398－402.

［3］ Li Na，Zhang M T，Deng Shiming，et al.Single－station performance evaluation and improvement in semiconductor manufacturing：agraphical approach ［J］.International Journal of Production Economics，2007，107 （2）：397－403.

［4］ Christian H，Cuneyt E，Adriana R H.The effect of lean production on financial performance：the mediating role of inventory leanness［J］.International Journal of Production Economics，2012，138（2）：242－253.

［5］ 沈维雷，黄 莉.基于组合赋权的装配线作业人员优化配置［J］.合 肥 工 业 大 学 学 报：自 然 科 学 版，2013，36（9）：1034－1037.

［6］ 应国柱，汪鹏程，朱大勇，等.模糊层次分析的改进及其在地铁施工风险评估中的应用［J］.合肥工业大学学报：自然科学版，2014，37（10）：1244－1248.

［7］ Sun C C.A performance evaluation model by integrating fuzzy AHP and fuzzy TOPSIS methods［J］.Expert Systems with Applications，2010，37：7745－7754.

［8］ 赵 锦.基于灰色关联模型的水电产业与经济发展关联分析［J］.统计与决策，2014（23）：149－151.