轮胎有限元建模过程优化及刚度特性仿真研究
2015-03-11哈斯巴根
哈斯巴根, 朱 凌, 石 琴, 张 雷
(1.合肥工业大学 交通运输工程学院,安徽 合肥 230009;2.安徽江淮汽车股份有限公司,安徽 合肥 230091)
汽车的操纵稳定性、碰撞侧翻安全性、行驶平顺性等均与轮胎的刚度特性有关[1]。有限元分析软件的引入为研究和设计整车带来了极大的方便,但由于轮胎几何结构的复杂性与材料的多样性,研究工作者一直探索如何建立兼具效率与精度的有限元轮胎模型。轮胎的理论分析模型近年来已较为完善,无论是基于纯理论的剪切力与回正力矩函数模型[2]还是基于半经验公式[3]的模型都能很好地求解侧偏刚度在内的轮胎力学特性。为了有效利用有限元软件研究车辆的各类行驶特性,轮胎的有限元建模研究也逐步深入。20世纪90年代以来,研究人员利用有限元软件建立轮胎二维断面模型研究其充气力学特征[4]。随后,汽车厂商利用壳单元模型研究车辆的碰撞安全。近年来更为复杂化的轮胎有限元模型可以模拟不同花纹[5]对轮胎行驶的影响及利用流固耦合原理模拟轮胎在雨雪路况下[6]的行驶。
随着对汽车性能的深入研究,研究人员与汽车厂商更加注重汽车在各种不同路况下行驶时整车的操纵稳定性、平顺性及其在发生侧向碰撞、刮擦、翻转等情况时的整车安全性,这对轮胎有限元模型精度及其在整车模拟中表现的稳定性与计算效率提出了更高的要求,上述过于简单或过于复杂的轮胎模型都无法满足要求。本文以128 205/60R16子午线轮胎为研究对象,研究了轮胎有限元建模过程的优化方法和途径。
1 轮胎有限元建模过程的优化
1.1 轮胎模型简化
子午线轮胎由多种材料复合压制而成,结构多层、变形复杂,体现很强的非线性。根据有限元离散计算原理,必须就具体的工况,在建模中对轮胎各部分进行简化。常用的有全实体单元模型和基于Belytschko-Tsay积分的壳单元模型。
壳单元模型将成型轮胎整体视为复合试件,进行材料单轴拉伸试验,取得材料参数。同时,在几何上省略三角胶、胎圈包布、钢丝圈等部分,只保留轮胎的基本几何外轮廓。建模中,Belytschko-Tsay壳单元属性赋给轮胎所有单元。此简化模型在径、侧向荷载加载的简单力学工况中可用,而且,所建立的同尺寸轮胎模型中只包含2 624个单元,仿真过程的计算速度快、效率高。但在不平坦路况、碰撞、侧翻等工况下,单一的材料设置无法体现轮胎各部分不同的线性或非线性特征,会导致变形过度,模拟失效。
实体单元模型详细地模拟轮胎各组件,特别是细化了胎面和胎侧(它们承担摩擦作用,保证变形稳)定。因而,在利用ALE方法仿真轮胎水滑行驶时,得到广泛应用。但由于包布、胎肩等部件外形不规则,在建模中常产生过多的不合格网格,容易导致仿真精度下降,甚至失效。基于上述原因,本文拟采用梁、壳及实体单元组合的模型,省略对轮胎性能仿真影响较小的部件,重点优化胎面、胎侧、帘线层等主要组件的建模过程。
1.2 轮胎二维断面曲线尺寸模型的确定
由于拟使用一、二维单元来模拟除胎面以外的其他各部分,因而仅绘制轮胎的断面外轮廓即可。轮胎的外缘由多条二次曲线相交拼接而成,研究中常使用控制点法进行测量,但相比于实际尺寸会有很大误差,影响力学性质。
本文采用经验推导公式[7],利用外径、断面宽度(B)、断面高度(H)、宽高比、轮毂直径(Rm)等基本参数推导计算出轮胎的行驶断面宽度(b)、胎冠弧度半径(Rn)、上下胎侧圆弧半径(R1、R2)、胎圈弧度、子口着合宽度(C)等参数。
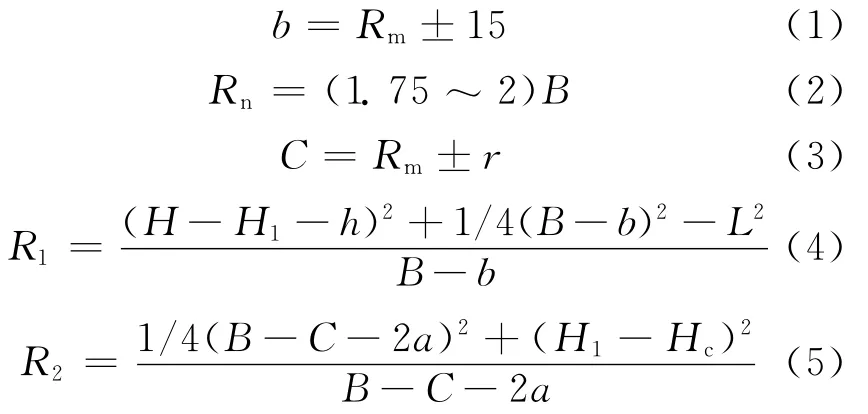
其中,r=1.0~1.5″;h为行驶断面弧高度;L为肩下反弧长度;H1为断面下部高度;Hc为轮毂曲线高度;a为轮毂曲线宽度的2/3。轮胎二维断面如图1所示。
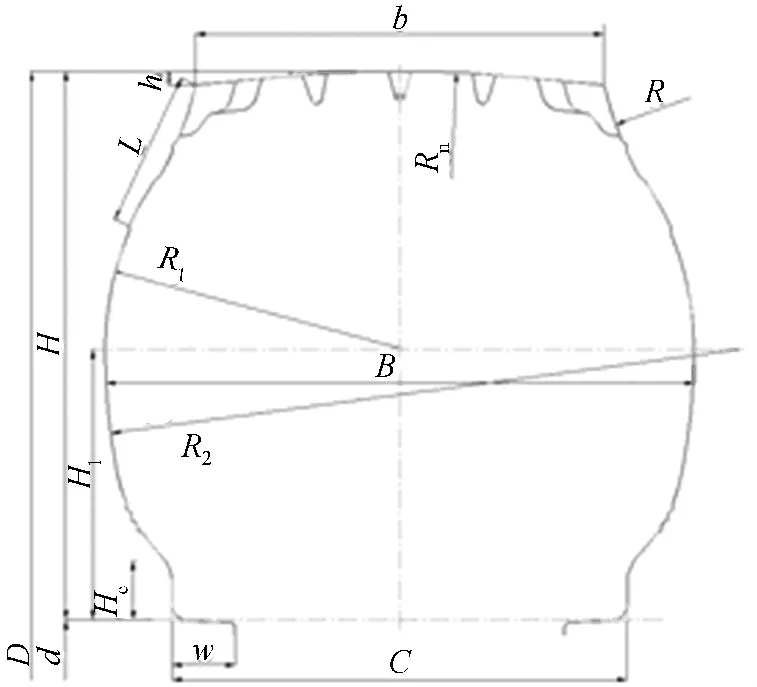
图1 轮胎二维断面
1.3 轮胎三维有限元建模的优化
(1)组合单元模型构成。梁、壳、实体组合模型由4个部分组成——实体单元构成的胎面、壳单元构成的胎侧、梁单元构成的帘线层与带束层,如图2所示。
(2)胎面。胎面由多种橡胶复合压制而成,承担与地面的相互作用力。在处理接触时,虽然可以通过SOFT、IGAP等命令减小接触刚度、强行忽略过度穿透,但随着行驶速度增加,接触愈加复杂,还是会出现不合理变形。因而,建模中需要充分考虑几何及网格划分的具体方式,以提高求解效率。LS-DYNA通过计算时间步长Δt来显示模型求解速率,即

对于壳单元网格:
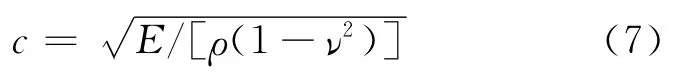
对于实体单元网格:
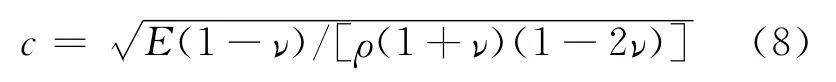
其中,E为材料杨氏模量;ν为材料泊松比;ρ为材料密度;lc为单元特征长度。对于三维实体单元与壳单元,在LS-DYNA中使用ISDO命令设置相同的非退化计算公式计算单元特征长度。
从(6)~(8)式可知,网格尺寸和材料会影响求解时间,因此,胎面采用相同尺寸的网格和统一的超弹性橡胶材料。经过仿真对比,采用1 696mm3的六面体实体单元,后处理文件d3hsp显示Δt约为0.013ms。与其长宽相同的壳单元的Δt约为0.008 2ms。两者相差不大,说明在不考虑其他影响因素的情况下,2种单元具有相近的求解速率。
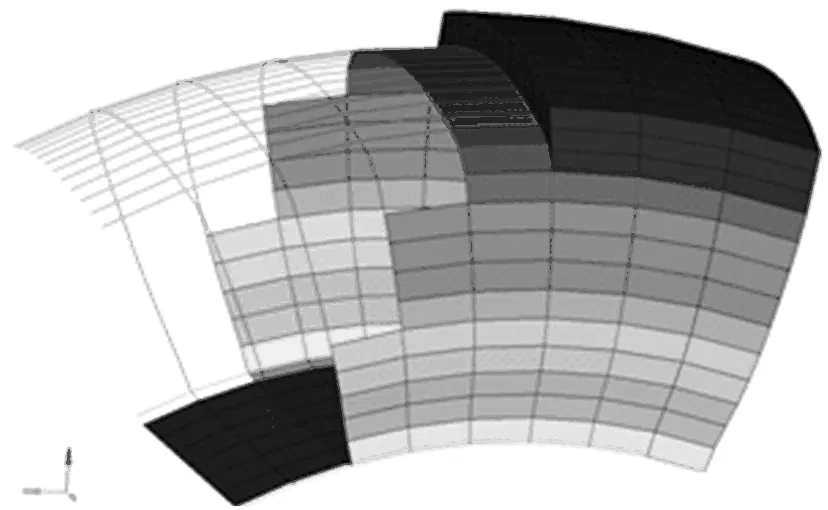
图2 梁壳实体联合轮胎模型
(3)胎侧。胎侧不直接与地面接触,只受径向力,因而采用壳单元可以减少单元与节点数量,提高效率。
建立胎侧部分时,采用以下方法:① 按照胎面网格大小,将胎侧分为不同厚度的8个部分,共2 368个壳单元;②采用Belytschko-Tsay缩减积分单元与复合弹性材料;③忽略三角胶、子口胶、胎肩反弧等部分;④采用一维梁单元嵌于胎侧、轮毂的连接位置,模拟子口钢丝圈,保证连接部分稳定变形。
(4)带束层。主要受力部件带束层,使用多层钢丝或纤维呈角度地铺设在胎面之下,正交于帘线层。受此启发,采用一维梁单元模拟周向钢丝纤维带束层,通过设置梁的方向达到与帘线层的垂直正交,相比于在胎侧内贴合实体单元的模拟方法[8],梁单元的计算步长Δt更大,求解时间会更短。
LS-DYNA中的合力梁单元不但可以拉伸、弯曲,还可以向其他结构传递受力。本文中梁单元的数量受到与之耦合的胎侧单元限制。各项异性材料的参数按照实际带束结构进行测量、拟合,以保证准确性。具体到梁单元方向时,如图3所示,根据以下方程,其在j方向与k方向的不同位移会引起相对方向剪力与弯矩变化。
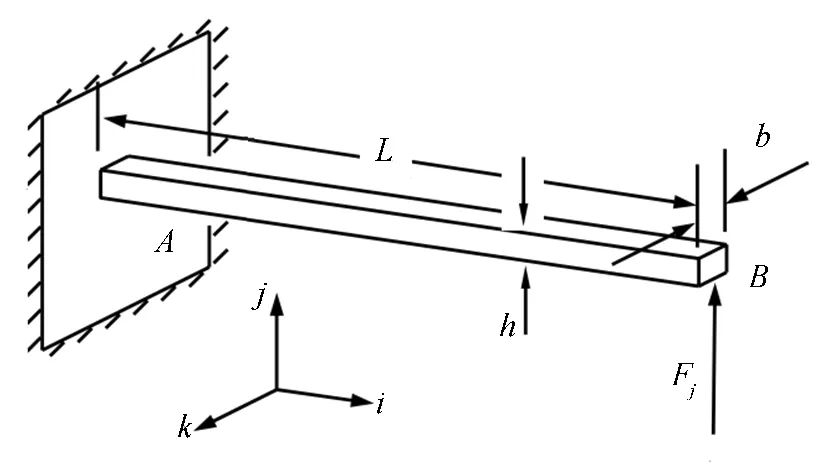
图3 梁单元受力模型
j方向产生位移时,有
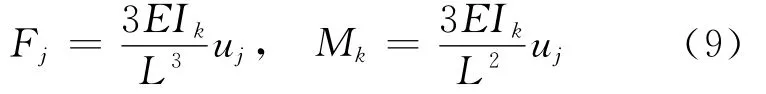
k方向产生位移时,有
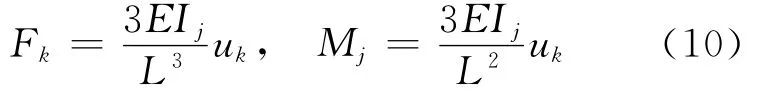
其中,Fj、Fk为2个方向所受剪力;Mj、Mk为2个方向所受弯矩;Ij、Ik为2个方向的惯性矩;uj、uk为2个方向的位移;E为弹性模量。
因而,模拟中要注意i-j-k局部坐标的设定。本文设定轮胎的前进方向为i,径向方向为k,侧向方向为j。利用右手准则,通过位于梁上、胎心的3点,赋给梁单元相应的坐标方向。
(5)帘线层。帘线层用于增加横向稳定性和胎侧刚度,铺设方向与带束层垂直。建模方法和带束层相同。由于帘线层横向贯穿整个轮胎内部,其各位置的受力方向均不相同,所以为各梁设定指向轮心的法向方向,以保证各条帘线受力和变形的一致。
2 轮胎优化模型的各工况模拟分析
2.1 不同精度轮胎模型的行驶工况分析
针对3种模型,模拟部分行驶工况,横向对比各模型的优劣。全实体单元的模型包含最多的单元数量与参数信息,理论上准确性高于其他2种模型,但在滚动行驶工况中,求解时间过长,甚至超出计算内存,不符合效率要求。
采用另2种模型分别模拟稳态侧偏、通过路缘石、管状路3种工况[9],仿真对比如图4、图5所示。从图4中可以发现,壳单元模型的整体变形并不符合轮胎正常的侧偏变形,出现了较大的侧倾,接地细部也出现了明显的过度变形;同样的情况出现在通过路缘石的路况模拟中。
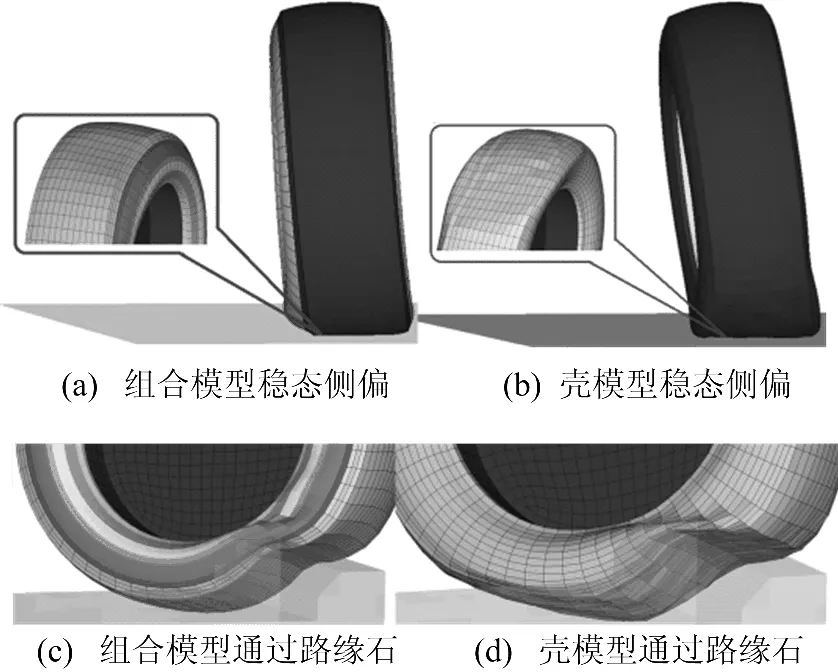
图4 2种模型的工况仿真对比
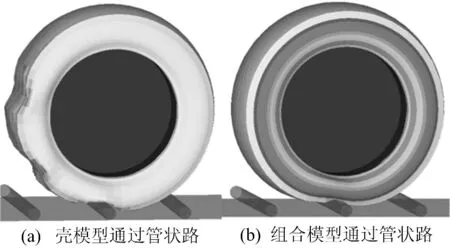
图5 2种模型的行驶工况仿真对比
从图5中可以发现,壳单元模型的材料单一,在变形后,很难在荷载撤销后恢复,不符合真实的情况。而且仿真中,轮胎的前进速度设为试验室测试所用的1km/h。若再模拟正常行驶速度,壳单元模型一定会产生连续的过度变形而导致模型不可用。
2.2 刚度特性分析
2.2.1 工况加载设定
径向加载工况中采用收敛性最好的轮毂固定、在地面上作用位移的加载方式[10]。对于侧偏工况,试验中很难模拟高速行驶中外力所致的侧偏现象,故采用向地面试验台增加转角的简化方法模拟侧偏角的输入。为保证准确性,模型尽可能准确地实现试验方法。
2.2.2 径向刚度分析
径向刚度的仿真分析及试验结果如图6所示。由图6可知,径向力随径向位移增大而增大。仿真值与试验值相近,计算可得径向刚度为214.4N/mm。为了更好地模拟充气轮胎的性能,采用了LS-DYNA中特有的空气包,模拟各种工况中膨胀压缩形变。
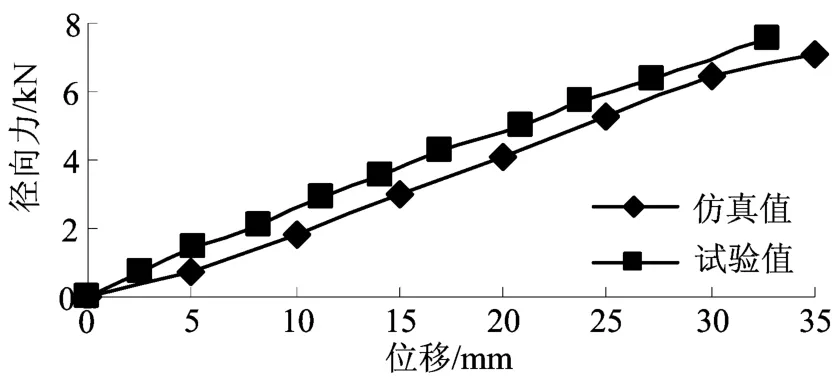
图6 径向刚度的仿真分析及试验结果
荷载加载速度会影响模型的受力。实际试验中0.000 5mm/s的加载速度置于仿真模型中,会使模型求解时间过长,经过速度从快到慢多组模型求解对比,发现求解速度达到0.035mm/s后,求解的受力较为稳定并与试验值接近,且求解的时间也相对较短,因而采用此加载速度可以进一步提高模型求解效率。仿真结果如图7所示。
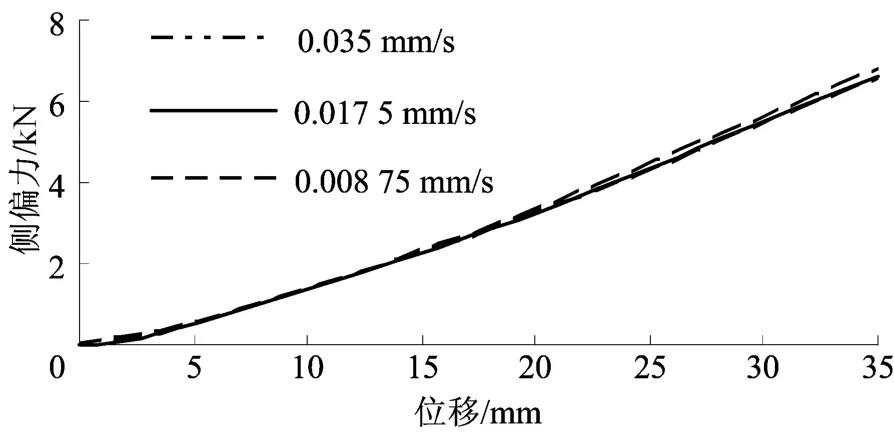
图7 不同求解速度下的仿真结果
2.2.3 侧偏刚度分析
侧偏刚度的仿真分析试验结果如图8所示。由图8可知,轮胎的侧偏刚度仿真值与试验值比较接近,但在仿真加载初期,即侧偏角小于2°时,仿真值与试验值存在5%~10%的误差。但模型基本可以反映实际的侧偏刚度特性。
3 结束语
本文利用LS-DYNA软件对子午线轮胎128 205/60R16的建模进行优化,采用梁壳实体单元耦合的方法分别模拟轮胎各部分结构。特别是采用梁单元模拟对轮胎受力性能及行驶工况有很大影响的带束层与帘线层,相比于全实体的模型,可以节省50%以上的运算时间。而在模拟管状道路、通过路缘石等工况时,也未出现单层壳网格模型中出现的变形过度、沙漏现象。
在对轮胎力学刚度特性模拟时,径向刚度在线性范围内的误差为7%左右。轮胎的变形与刚度特性接近实际的行驶工况下测得的试验值。侧偏刚度在小侧偏角下与试验值有微小差距,但均在可接受的范围内。因此,模拟是合理可接受的。经过与试验验证,此优化方法是可行的,仿真的精度可以通过对接触、材料属性的进一步调整更接近实际行驶工况。
[1] 余志生.汽车理论[M].第5版.北京:机械工业出版社,2009:104-113.
[2] 郭孔辉,刘 青.稳态条件下用于车辆动力学分析的轮胎模型[J].汽车工程,1998(20):129-134.
[3] 刘 青,郭孔辉.轮胎侧偏特性研究的特点及其发展[J].汽车工程,1997(10):1-8.
[4] Lee C R,Kim J W,Hallquist J O,et al.Validation of a FEA tire model for vehicle dynamic analysis and full vehicle real time proving ground simulations,SAE Technical Parper 971100[R].SAE,1997.doi:10.4271/971100.
[5] 曾 光.计及胎面花纹影响的轮胎侧偏显示有限元分析[D].合肥:中国科学技术大学,2009.
[6] 徐新泉,刘 伟,刘 焜.湿滑路面上固体颗粒对轮胎附着性能的影响[J].合肥工业大学学报:自然科学版,2012,35(2):149-152,229.
[7] 辛振祥,邓 涛,王 伟.现代轮胎结构设计[M].北京:化学工业出版社,2011:115-119.
[8] Hall W ,Jones R P,Mottram J P.Tire modeling mthodology with the explicit finite element code LS-DYNA[J].Tire Science and Technology,2004,32(4):236-261.
[9] Reid J D,Boesch D A,Bielenberg R W.Detailed tire modeling for crash applications[J].International Journal of Crashworthiness,2007,12(5):147-162.
[10] 臧孟炎,许玉文,周 涛.三维非线性轮胎的五刚特性仿真[J].华 南 理 工 大 学 学 报:自 然 科 学 版,2011,39(1):129-133.
