基于mNLS方程的周期波群非线性演化数值模拟研究

张本辉 石爱国 蔡 烽 王 骁 周 波

(1.海军大连舰艇学院航海系 大连 116018)(2.海军大连舰艇学院基础部 大连 116018)



基于mNLS方程的周期波群非线性演化数值模拟研究

张本辉1石爱国1蔡 烽1王 骁1周 波2

(1.海军大连舰艇学院航海系 大连 116018)(2.海军大连舰艇学院基础部 大连 116018)

论文基于控制深水复波包络演化的修正的四阶非线性薛定谔方程(mNLS)建立模型,利用离散时间步长的虚拟频谱方法(split-step pseudospectral method)进行求解,模拟了周期波群的非线性演化,对演化过程中复包络幅值、波面位移、谱成分能量以及模态值的变化进行分析。结果表明:该模型可以有效地模拟周期波群的非线性演化。

四阶非线性薛定谔方程; 虚拟频谱方法; 数值模拟; 周期波群

Class Number O175; TP391

1 引言

随着我国经济和综合国力的显著提高,国家海外利益的不断拓展,国家对海洋的关注程度也越来越大。与此同时,伴随着中国海军逐步从近海走向深蓝,我海军维护海洋权益的使命日益繁重。在我国海军“走出去”的过程中,海浪环境深刻地影响舰艇的航行和作战效能,因此如何更加准确地把握远洋海区风浪环境的特点和规律,对我海军战斗力的生成具有显著作用。

目前,从流体力学基本方程出发,对于深水波浪数值模拟方法大多是基于线性海浪模型。近些年来大量的外海观测和实验室实验已经反复证明,实际的海浪是非线性的,其主要表现有这样几个方面:波高的非瑞利分布、双峰乃至多峰海浪谱的大量存在、波浪变形及破碎以及海浪的非线性局域化特征等[1]。随着海洋科技的发展和大量海洋工程的迫切需求,线性海浪模型已日益不能满足越来越高的精度要求,因此对海浪的非线性研究也得到了众多海洋科技工作者的关注[2]。研究能够反映海浪非线性特征的数值模拟方法是未来的发展趋势[3],使用非线性演化理论来模拟深水海浪将会更加合理有效。

Philips阐述了弱非线性共振相互作用的机制,为非线性深水波的研究奠定了基础。速度和波长稍微有差别的几个波列的共振相互作用涉及正弦波的缓慢调制,波列之间会产生能量交换,Stokes波对于缓慢调制的周期性(边带)扰动来讲是不稳定的,Benjamin和Feir[4]对于这一事实的论证做了关键性的工作,初步证实了深水波列传播过程中的演化具有不稳定性,该不稳定性在波陡明显小于碎波条件时也会发生,这一点与真实深水波浪的情况比较吻合,透过这个问题的研究,有助于了解实际海面上波群的形成与演化特性[5]。基于窄谱假设和弱非线性假设,Zakharov、Benney和Roskes通过非线性和色散性推导得到了描述表面振幅包络波演化的三阶非线性薛定谔方程,该方程具有波陡的三阶精度。而三阶非线性薛定谔方程比较适合于描述具有较小波陡(小于0.1)的波列演化,对于较大的波陡,其模拟结果只是在波列演化的初期符合实际情形,无法准确地模拟长时间的波列演化。为了进一步克服三阶方程之不足,Dysthe[6]考虑由辐射应力引起的平均流效应,推导出了四阶Dysthe方程,Lo和Mei[7]对该方程进行小的修正,得到了修正的四阶非线性薛定谔方程(mNLS)。因此本文基于mNLS建立描述周期波群的演化模型,以期探讨深水波列的演化规律。

2 深水波列数学模型

2.1 控制方程

通常在无粘无旋的假设条件下,海面上的波浪运动可以通过速度势函数的拉普拉斯方程和自由表面及海底等边界条件来描述,利用泰勒级数展开,将自由面边界条件展开到O(ε4)四阶形式(波陡ε=ka,k和a分别表示载波波数和波幅),经过推导和变换(具体过程可以参考文献[7]),可以得到群速度移动坐标系统下的四阶非线性薛定谔方程为

(1)

(2)

方程(1)等号右边考虑了平均流影响并以移动坐标计算到四阶的新增部分,如果忽略方程中的四阶项,则简化为相应的三阶方程,如果忽略所有的非线性项,则进一步简化为对应的线性方程。根据方程(1)和方程(2)可计算出波面位移,无因次的自由波面位移为

(3)

A(0,η)=A(2π,η)

(4)

A(0,z,η)=A(2π,z,η)

(5)

2.2 离散步长的虚拟频谱方法

对于NLS方程而言,可以利用逆散射变换求取其精确的解析解[8]。四阶非线性薛定谔方程一般情况下不适合于解析求解,因此迫使人们借助于各种各样的数值算法。离散步长的虚拟频谱方法[9～10]是一种有效求解mNLS方程的数值求解方法。该方法主要分为两个部分,虚拟频谱方法和中心有限差分法。虚拟频谱方法是一种以傅里叶变换为基础的方法,需要满足周期性边界条件方程(4)和方程(5),可以有效地求解mNLS方程的线性部分。在数值计算中,将控制方程(1)分为线性部分(方程(6))和非线性部分(方程(7)):

(6)

(7)

复波包A(ξ,η)(0<ξ<2π)的傅里叶空间上的变换及逆变换如下所示:

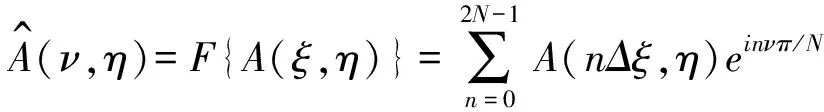
ν=0,±1,±2,…,±N,Δξ=π/N

(8)

(9)

其中2N为周期2π上的离散点数,Δξ=π/N,当ν≠±N时,μν=1;当ν=±N时,μν=1/2。

在每一个空间步长上,非线性部分的解作为线性部分的初值代入并求解,从而得到下一步方程的解,然后把线性部分的结果再代入非线性部分方程,从而依次递进求解。

3 数值仿真

3.1 初始条件

为了验证周期波群的包络以群速度传播且不改变形状,Keller(1982)采用两个组成波合成的周期波包作为初始条件进行了水槽试验,试验中沿水槽布置了10个观测点,距离造波机7.14m的初始范围内的波浪记录是有效的,具体位置如图1所示。其初始条件的参数如下:周期波包的组成波频率分别为f1=1.406Hz和f2=1.563Hz,定义平均频率f=1.485Hz为载波频率,对应的k=8.865m-1。初始载波振幅为零,两个组成波的振幅为0.5a=0.013m,波陡为ε=0.23,令λka=Δω/ω,复波包初始条件为

A(ξ,0)=0.483eiξ+0.537e-iξ

(10)

以该周期波包作为初始条件,采用本文所建立的数值模型来进行数值模拟,然后与实际试验数据进行比对。

3.2 仿真结果分析及讨论

3.2.1 非线性演化过程中的波形比对

数值模拟的结果与Keller试验中八个测量点处的波面比较如图1所示(图中也给出了对应的三阶方程的模拟结果)。

图1 数值模拟的波面与实测水位的比较

从图中可以看出,在距离造波机比较近的几个位置(η=1.47,η=1.73,η=2.01)处三阶方程的数值结果和试验结果比较吻合;当η=2.28时,三阶方程的结果开始偏离试验结果;当η=3.35时,三阶方程的结果已经与试验结果存在相当大的差异,而四阶方程的数值结果一直与实验结果吻合良好。另外,从图中可以看出,波形上下、左右呈现出非对称性。

3.2.2 非线性演化过程中的谱成分比对

为进一步研究周期波群非线性演化过程中能量的变化,因此对复波包A的谱成分(ν=±1,±3)进行分析,NLS方程和mNLS方程的复波包谱成分振幅的变化如图2和图3所示。

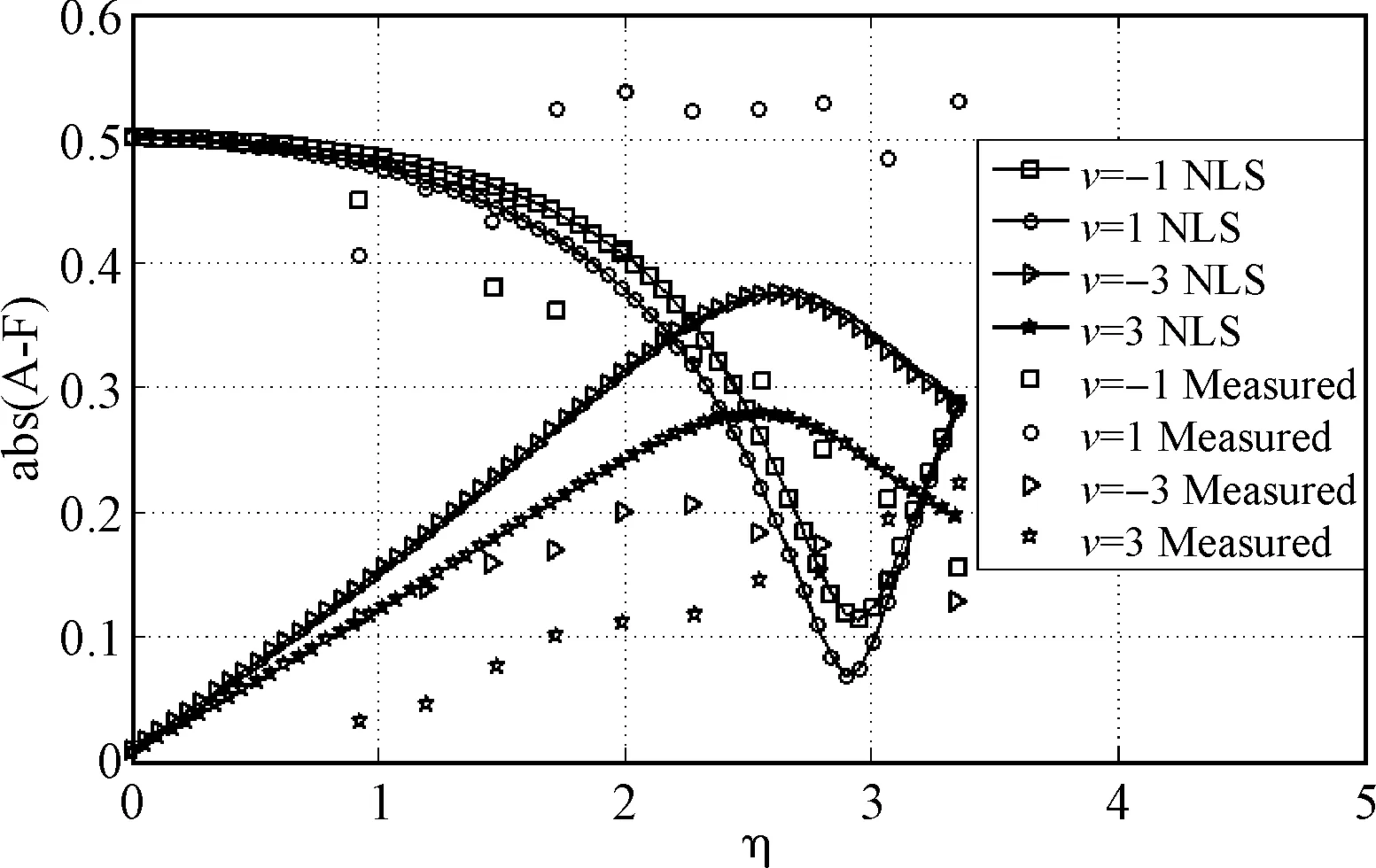
图2 测量值和NLS模型数值计算得到的谱成分能量的比较

图3 测量值和mNLS模型数值计算得到的谱成分能量的比较

由图2和图3对比可知,NLS模型的数值计算结果与实测值偏差较大,mNLS模型数值计算得到的谱成分能量和试验测量值更加一致,虽然mNLS的数值计算的结果无法与实验值完全吻合,但就整体演变趋势而言,大致与实验值相符合。究其不同,则是mNLS方程比NLS方程多的两个四阶项的作用引起的。

3.2.3 非线性演化过程中的mNLS方程五项模态值的变化

mNLS方程中五项模值随演化距离的变化如图4所示。

从图4中可以看出,初始时刻控制方程中各项模的幅态值很小,变化幅度不大,方程的第五项,即平均流项模态值接近于零,因而在初始阶段该项的作用很小;随着周期波群的演化,方程的各项模态值不断增长;在η=6时,方程第四项(四阶项)模态值甚至超过了方程的第三项(三阶项)。另外,从图4中可以看出,η=0和η=10时,控制方程的对应的模态值比较接近。

图4 周期波群演化过程中mNLS五项模态值变化

3.2.4 周期波群的长距离非线性演化

为了进一步了解周期波群演化的整体情况,复波包振幅的时空变化如图5所示。

由图5可知,初始的周期波群在η=3.3附近开始分裂,而在η=11附近又重新演变成一个波群,和初始位置的波群非常接近,展示了波群演化过程中的边带不稳定性。一个原始的周期波群分裂成两个波群,幅值比较高的波群传播得快,因此,较高的波群最终能追上较低的波群,并且合并在一起。周期波群外在波形的变化实际上是由其内在能量的变化所决定的,图5对应的谱能量变化如图6所示。

图5 周期波群复波包络的时空演化图

图6 周期波群演化过程中谱成分能量的变化

由图6可知,在周期波群演化过程中,波群能量在各个频率分量之间不断传递,与周期波群复波包络的时空演化是相对应的。在η=11处各个边带的能量状态和初始位置接近,近似于初始状态的再现,这样就完成了第一个能量传递的循环。

在整个演化过程中,复波包满足能量守恒定律,其相对误差不大于0.15%,确保了整个模型的有效性。

4 结语

本文以控制深水波列演化的mNLS方程为基础,研究了周期波群的时空演化,可以得到如下结论:

1) 对于周期波群而言,mNLS方程是NLS方程的拓展,可以预测其长时间演化。相对NLS方程而言,mNLS方程的谱成分随距离的演化与测量值更加吻合。

2) 在周期波群非线性演化过程中,四阶项的作用非常重要,不能被忽略掉。

3) 能量在不同的谱成分之间相互传递,外在表现为周期波群的分裂与复合。

本文的数值模拟并没有考虑阻尼、破碎等因素的影响,这些因素对与波群演化的影响也是需要下一步进行研究的。

[1] 蔡烽,缪泉明,顾民,等.海浪的非线性效应及其产生原因[J].中国造船,2006,47(11):153-159.

[2] 蔡烽,沈泓萃,缪泉明,等.海浪非线性行为的参数化表征[J].船舶力学,2008,12(2):157-167.

[3] 聂卫东,康凤举,褚彦军,等.基于线性海浪理论的海浪数值模拟[J]系统仿真学报,2005,17(3):1037-1044.

[4] Benjamin T B, Feir J E. The disintegration of wave trains on deep water Part1[J]. Journal of Fluid Mechanics,1967,27(3):417-430

[5] 胡凯程.深水非线性波列调变之数值解析[D].台湾:国立成功大学,2004.

[6] Dysthe K B. Note on a modification to the nonlinear Schroedinger equation for application to deep water waves[C]//Proceedings of the Royal Society of London Series A-Mathematical Physical and Engineering Sciences, London,1979:105-114.

[7] Lo E, Mei C C. A numerical study of water-wave modulation based on a higher-order nonlinear Schroedinger equation[J]. Journal of Fluid Mechanics,1985:395-416.

[8] A. R. Osbrone. Nonlinear ocean waves and the inverse scattering transform[M]. 2010.

[9] 张运秋,张宁川,裴玉国.畸形波数值模拟的一个有效模型[J].大连理工大学学报,2008,48(3):406-410.

[10] 张运秋,胡金鹏.畸形波生成的一种非线性机理分析[J].华南理工大学学报,2009,37(6):117-123.

Numerical Simulation on Nonlinear Evolution of the Periodic Wave Groups Based on nMLS Equation

ZHANG Benhui1SHI Aiguo1CAI Feng1WANG Xiao1ZHOU Bo2

(1. Navigation Department, Dalian Naval Academy, Dalian 116018) (2. Basic Science Department, Dalian Naval Academy, Dalian 116018)

A numerical wave model based on the modified fourth-order nonlinear Schrodinger equation(mNLS) was developed to describe the evolution of deep-water wave envelope and a split-step pseudo-spectral method was used to solve the equation, simulating nonlinear evolution of the periodic wave groups and analyzing the changes of the complex envelope amplitude, wave surface displacement, spectral component energy and modulus value in the evolutionary process. Results showed that the model can effectively simulate nonlinear evolution of the periodic wave groups.

fourth-order nonlinear Schrodinger equation, split-step pseudo-spectral method, periodic wave groups, numerical simulation

2015年1月13日,

2015年2月18日 作者简介:张本辉,男,博士研究生,研究方向:非线性海浪及舰船耐波性。石爱国,男,教授,研究方向:舰船操纵性与耐波性。蔡烽,男,博士后,副教授,研究方向:海浪非线性建模及仿真。王骁,男,博士,讲师,研究方向:海浪非线性建模及仿真。周波,女,博士,副教授,研究方向:海浪谱预报。

O175; TP391

10.3969/j.issn1672-9730.2015.07.029