北斗三频周跳探测与修复算法研究
2015-03-10谢兰天赵乐文叶世榕
谢兰天,赵乐文,叶世榕
(武汉大学 卫星导航定位技术研究中心,武汉430079)
北斗三频周跳探测与修复算法研究
谢兰天,赵乐文,叶世榕
(武汉大学 卫星导航定位技术研究中心,武汉430079)
载波相位观测值已越来越多地应用到增强系统中,由于观测环境影响,载波相位测量不可避免地会产生周跳,周跳的成功探测与修复是提高导航定位精度的一个重要因素。针对北斗卫星导航系统三频观测数据,分析其不同线性组合观测值的特性,选取合适的组合系数,形成一个伪距相位组合和两个无几何相位组合,采用历元间差分的方法探测和修复组合观测值的周跳,然后还原求解出原始信号的周跳,最后通过实验验证了该方法的可行性。
北斗卫星导航系统;三频;周跳;伪距相位组合;无几何相位组合
0 引言
由于观测环境影响,载波相位测量不可避免地会产生周跳,周跳的探测与修复是GNSS高精度定位的关键问题。目前已经可以获得GPS、COMPASS以及GLONASS等导航定位系统的三频载波观测值。用三频载波观测值可以组成不同的三频组合观测值,相比于传统双频观测值,三频组合观测值具有显著的优点:可以形成噪声更小、波长更长、电离层延迟更小等具有良好特性的组合观测值[1]。
目前常用的双频周跳探测方法包括:高次差法、TuberEdit、多项式拟合法、多普勒积分法、卡尔曼滤波法、小波分析法等[2]。其中研究和应用最广泛的是TuberEdit方法,这种方法不仅消除了电离层延迟,也消除了卫星钟差、接收机钟差和卫星至接收机的几何距离,相较于其他几种方法探测精度较高,也比较容易实现[3]。
对于用三频组合观测值的方法来探测和修复周跳,国内外学者也进行了相关研究。李金龙等[2]推导了用三频观测数据形成伪距相位组合,以组合后的组合周跳估值标准差最小为原则,选取合适的组合探测和修复周跳,但是这种方法的前提是忽略电离层延迟的影响,采样率稍大或者电离层活动剧烈就会对这种方法造成一定的影响;黄令勇等[4]提出用三频无几何相位组合与伪距/载波组合结合的方法探测周跳,但其周跳修复方法较为复杂;孙保琪和罗腾等[5-6]用三频伪距/载波组合法,选取合适的组合值探测和修复周跳,但是其周跳探测方法的三个组合都是伪距相位组合,受伪距测量的多路径效应和噪声影响比较大,且包含电离层延迟的组合没有处理,在采样率较大或者电离层发生剧烈不规则变化时,会降低探测效果。
本文提出了一种用三组线性无关的组合观测值联立求解的方法探测和修复周跳。考虑到伪距噪声比载波相位噪声大,为了减弱噪声影响,三组线性无关的组合观测值仅采用一个伪距相位组合和两个无几何相位组合,并对没有消除电离层延迟的组合进行电离层延迟改正,以减弱电离层延迟的影响。
1 三频组合观测值
在不考虑误差的情况下,记i、j、k为组合系数,载波相位组合观测值和伪距组合观测值可以写成式(1)、式(2)[7]:
(1)
(2)
组合观测值的整周模糊度为
Nc=iN1+jN2+kN3
(3)
为了保持整周模糊度的整数特性,i、j、k的取值也必须是整数。
组合观测值的频率为
fc=if1+jf2+kf3
(5)
组合观测值的波长为
(6)
2 误差分析
三频组合观测值仅受历元间电离层延迟变化量和观测噪声影响,与测站到卫星的距离、钟差等无关。
2.1 电离层延迟
根据电离层延迟定义,忽略高阶项,三个频率上的电离层延迟关系如下:
(7)
组合观测值的电离层延迟如下
(8)
2.2 观测噪声
假设三个频率下的观测噪声相同,并假设载波相位观测值的噪声大小为sj1=sj2=sj3=0.003m,伪距观测值的噪声大小为sP1=sP2=sP3=0.3m。
组合观测值的噪声eφ(i,j,k)和ep(i,j,k)为:
(9)
(10)
综合上述讨论,载波相位组合观测值可以写为
j(i,j,k)=r-b(i,j,k)I1-
N(i,j,k)l(i,j,k)+ej(i,j,k)
(11)
伪距组合观测值为
P(i,j,k)=r+b(i,j,k)I1+eP(i,j,k)
(12)
3 北斗三频周跳探测与修复
对于周跳探测和修复的问题,一般要求载波相位组合满足下面的条件[8]:
1)为了保证整周模糊度的整数特性,组合系数必须是整数;
2)具有较长的波长;
3)电离层延迟影响系数较小;
4)组合观测噪声较小。
为了选取三组合适的系数,针对北斗卫星,本文在表1中列出了各种不同系数组合的波长、电离层延迟以及噪声的影响。综合上述组合观测值选取条件,我们先选取了超宽巷组合(0,1,-1)和宽巷组合(1,0,-1)。为了能还原原始频率的周跳,选取的三组系数必须线性无关,因此本文第三组系数选取了窄巷组合(4,0,-3)。
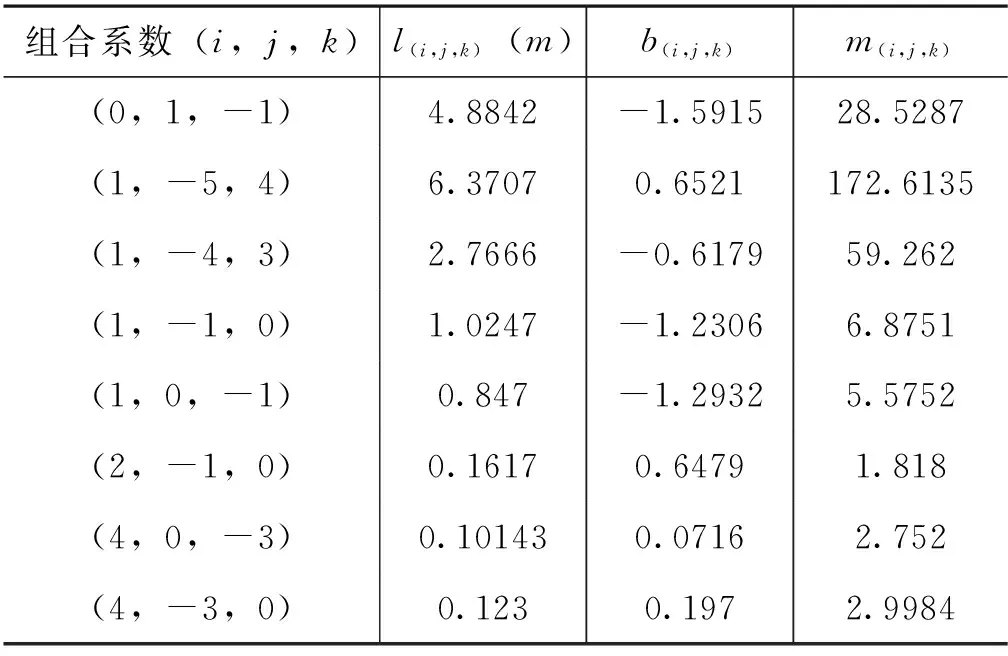
表1 北斗三频组合值参数计算Tab.1 Compass triple frequencycombined value parameter calculation
3.1 超宽巷周跳探测
对于超宽巷组合,本文采用伪距相位组合观测量,用下面的模型计算其组合周跳值[9]。
(13)

(14)
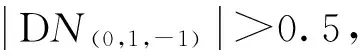
3.2 宽巷周跳探测
对于宽巷组合的处理,本文比较了两种计算方案。
3.2.1 方案A
采用伪距相位组合观测,仍然用式(13)计算,令(1,m,n)为(1,0,1),消除电离层延迟,结果如下
(15)
同样的,根据方差-协方差传播定律,可以计算出DN(1,0,-1)的标准差s(1,0,-1)≫0.35周,也小于0.5,因此阈值0.5仍然是合适的。
3.2.2 方案B
采用无几何相位组合观测,因为已经得到了超宽巷组合的结果,因此将模糊度固定的超宽巷作为精密伪距,来辅助宽巷周跳探测
j(0,1,-1)-j(1,0,-1)=
N(1,0,-1)l(1,0,-1)-N(0,1,-1)l(0,1,-1)+
(b(1,0,-1)-b(0,1,-1))I1
(16)
在历元间差分得到
DN(1,0,-1)= (Dj(0,1,-1)-Dj(1,0,-1)-
(b(1,0,-1)-b(0,1,-1))DI1+
(17)
通过计算得到,电离层延迟DI1的系数为0.298,相比于宽巷组合的波长,电离层延迟的差异在很短时间内的变化可以忽略不计。

3.2.3 两种方案比较
方案A的优点是消除了电离层延迟的误差,但是却引入了伪距观测值的噪声;而方案B刚好相反,引入超宽巷的结果,避免了伪距噪声的影响,但受到电离层延迟的影响。从上面的计算中可以看到,两种方法计算得到的标准差都小于0.5,但是通过方案B计算的宽巷组合的标准差比方案A计算的要小一些,一方面是因为电离层活动不剧烈,另一方面是与载波相位测量的噪声相比,伪距测量的噪声比较大。因此本文实验采用第二种方案。
3.3 窄巷周跳探测
在计算窄巷组合时,可将模糊度固定的宽巷作为精密伪距,来辅助窄巷周跳探测
j(1,0,-1)-j(4,0,-3)=
N(4,0,-3)l(4,0,-3)-N(1,0,-1)l(1,0,-1)+
(b(4,0,-3)-b(1,0,-1))I1
(18)
经历元差分后可以得到
DN(4,0,-3)= (Dj(1,0,-1)-Dj(4,0,-3)-
(b(4,0,-3)-b(1,0,-1))DI1+
(19)
经过计算可知,b(4,0,-3)-b(1,0,-1)=1.3648,而窄巷组合值的波长是0.1014m,波长相对于电离层误差较短,电离层延迟并不能忽略不计,尤其是当采样率高或者电离层活动剧烈的时候,因此在窄巷组合周跳探测时,电离层延迟必须实时更新。本文用下面的公式来计算电离层延迟的大小:
(20)
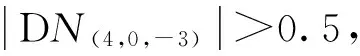
3.4 周跳修复
得到了组合观测值的周跳之后,用式(21)推导出原频率上的周跳值。
(21)

4 实验
本文使用2013年10月9日在武汉采集的三频数据对所研究的方法进行验证,所用数据的采样率为1s。共观测到了9颗北斗卫星,观测数据质量良好。由于本次观测到的卫星较多,下面仅给出C01、C02、C08和C09这4颗卫星的处理结果,其他卫星处理结果类似。
图1是4颗卫星在历元间电离层延迟的变化情况,即DI。分析图中结果可知,这4颗卫星在相邻历元间的电离层延迟变化量在±0.005m之间,说明在测量过程中电离层延迟的变化并不大,观测环境良好。
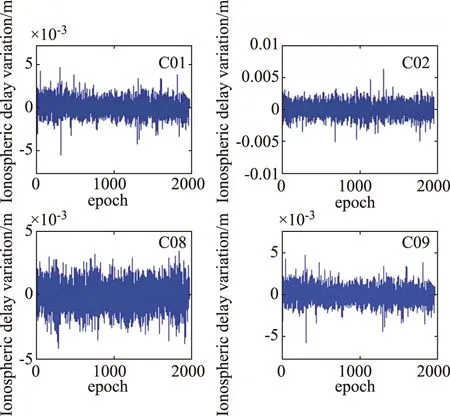
图1 C01,C02,C08和C09四颗卫星历元间的电离层延迟变化情况Fig.1 Ionospheric delay variation between epochs for four satellites C01,C02,C08 and C09
图2和图3分别为4颗卫星在各个历元DN(0,1,-1)、DN(1,0,-1)和DN(4,0,-3)的值。如果在观测值中不存在周跳的现象,忽略电离层变化的微小项,组合周跳值DN(0,1,-1)、DN(1,0,-1)和DN(4,0,-3)就代表着噪声的影响。从图2和图3中可以看到,这些组合值的随机噪声影响最大的不超过0.2周,而随机噪声影响小的甚至在0.05周以内。由此可见,本文设定0.5周作为探测修复周跳的阈值是可行的。
为了验证上述方法的有效性,本文对这次测量的数据进行了人为的加入周跳处理,在不同的卫星上加入了大小不同的周跳值,经过测试得到结果。
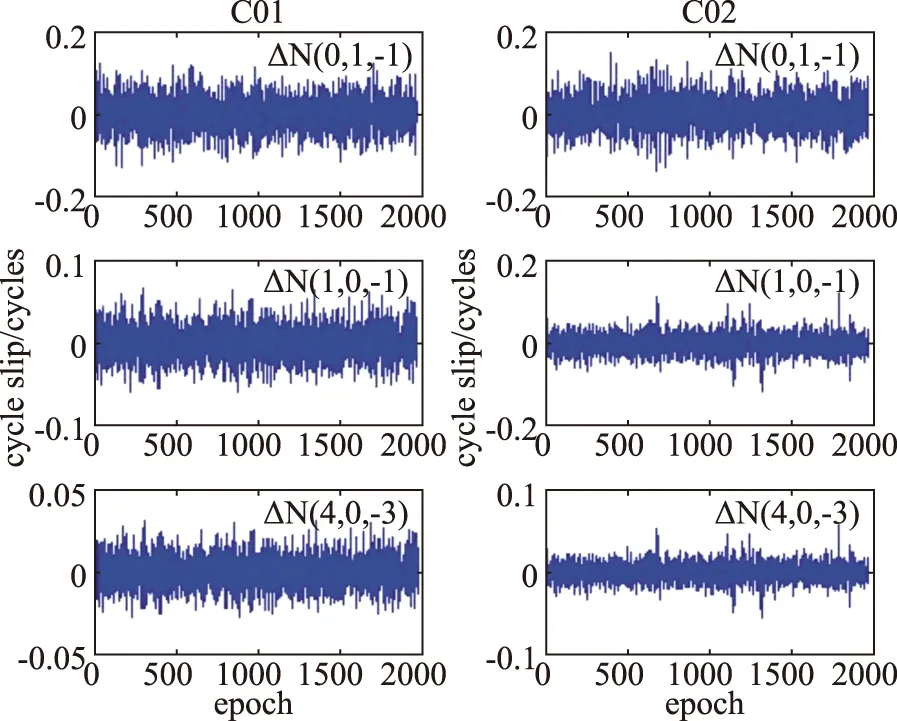
图2 C01和C02号卫星不同线性组合的组合周跳值Fig.2 Cycle slips of different linear combinations of satellite C01 and C02
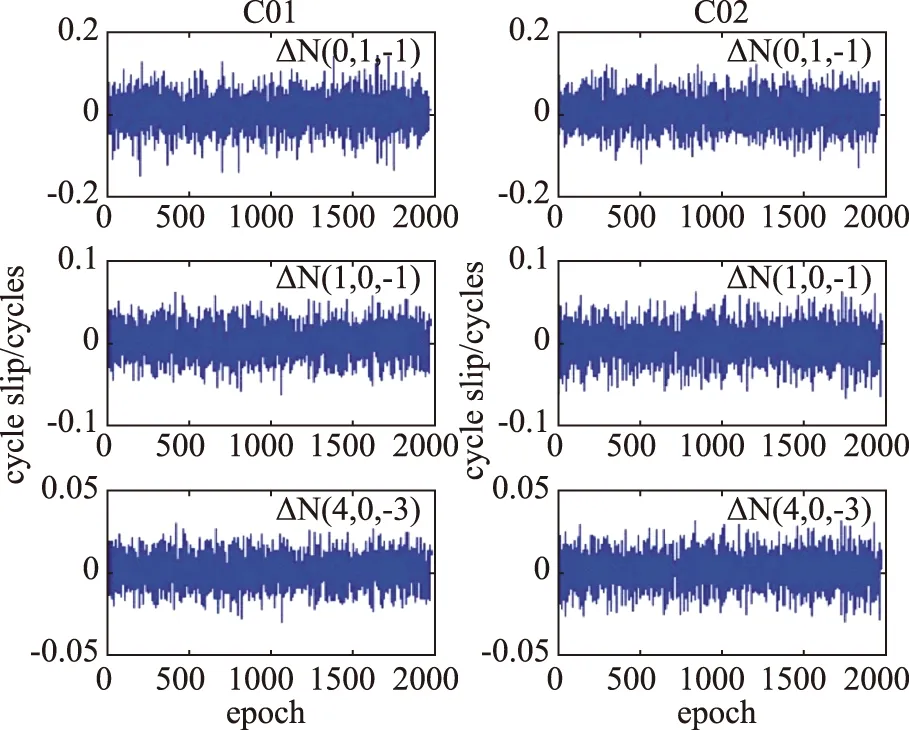
图3 C08和C09号卫星不同线性组合的组合周跳值Fig.3 Cycle slips of different linear combinations of satellite C08 and C09
在C01号卫星上加入了(1,0,0)的周跳值,得到的结果如图4;在C02号卫星上加入了(0,1,0)的周跳值,得到的结果如图5;在C08号卫星上加入了(0,0,1)的周跳值,得到的结果如图6。

图4 加入周跳后的C01号卫星结果图Fig.4 The result of satellite C01 after added cycle slips
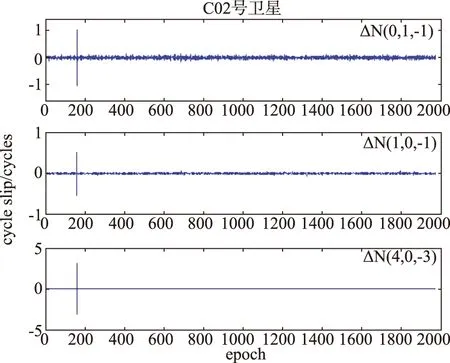
图5 加入周跳后的C02号卫星结果图Fig.5 The result of satellite C02 after added cycle slips

图6 加入周跳后的C08号卫星结果Fig.6 The result of satellite C08 after added cycle slips
从图4~图6中很明显地看到,这三组小周跳都被探测出来。如图4,在超宽巷组合的计算中没有涉及到B1信号的计算,因此ΔN(0,1,-1)的值并没有发生异常变化;而宽巷和窄巷组合的计算涉及到B1信号,由于在B1信号上加入了1周的周跳,因此导致了宽巷和窄巷组合的值出现异常,周跳被正确的探测到。图5和图6分别在B2和B3信号上加入了一周的周跳,因此,在计算中,图5涉及到B2信号的,图6涉及到B3信号的,组合周跳值都会出现异常。
在图4~图6中,探测到的周跳都有正、负两个值,符号相反,数值相同。这是因为在计算这些组合周跳值时,采用的是历元间差分的方法。假设在t历元加入了大小为n的周跳值,则在t历元的解算中,t历元和t-1历元的双差可以计算出存在(-n,0,0)的周跳,下一个历元t+1和历元t的差值刚好相反,探测到(n,0,0)的周跳存在。那么根据上面这个结果可以断定,周跳存在于t历元中,大小为(n,0,0)。据此可以判断出周跳发生的历元和大小。可以看到,图4、图5和图6都满足这种关系。
从上面的结果可以看到,对于大小仅一周的小周跳,本文提出的方法也能有效地探测出来,可见这种方法的精度比较高。为了更好地验证上述周跳探测方法的有效性,本文在原始数据的不同卫星、不同的频率信号上均加入了大小不同的周跳值,然后用上述方法进行探测,试验得到的结果如表2。
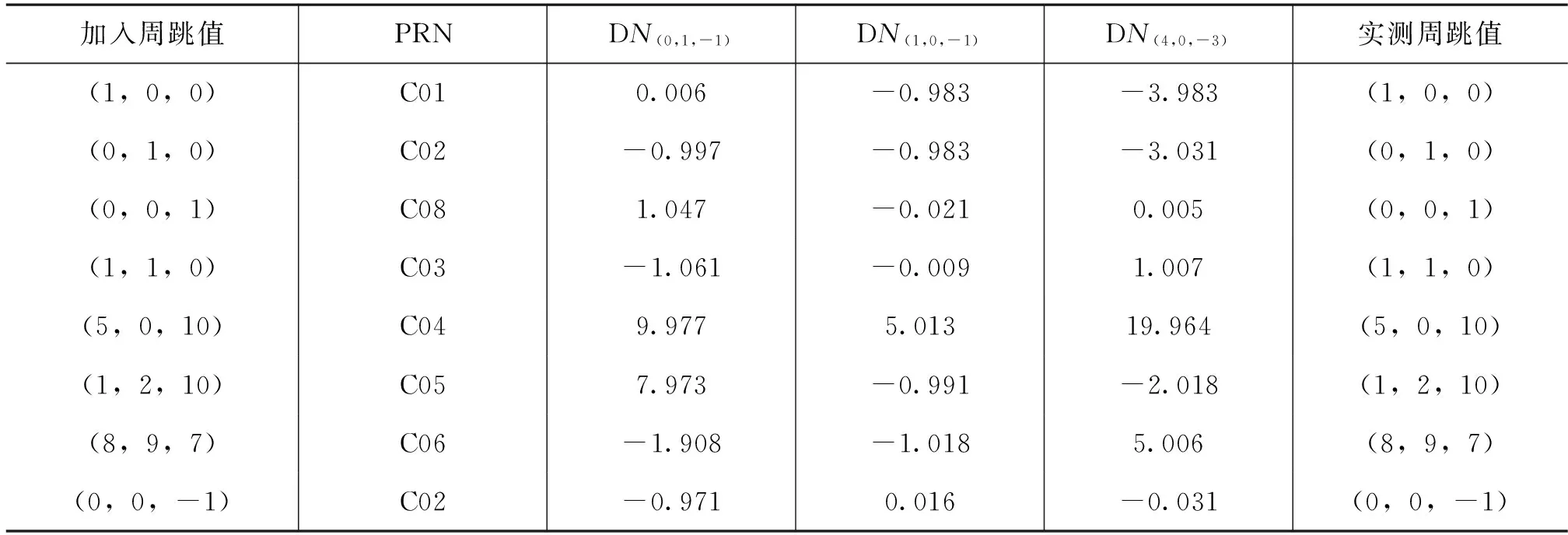
表2 加入周跳后的探测结果Tab.2 The result of detection after added cycle slips
从表2中可以看到,无论是哪颗卫星,是一周的小周跳还是十周的大周跳,也无论周跳发生在哪个信号上,本文提出的三频探测方法都能成功地探测到周跳,并且准确地给出周跳的大小。
5 结论
本文针对北斗卫星,提出了一种三频探测周跳的方法。该方法用三频数据的线性组合,选取超宽巷(0,1,-1)形成一个伪距相位组合,选取宽巷(1,0,-1)和窄巷(4,0,-3)形成两个无几何相位组合,并对电离层延迟做了相关处理,经过历元差分后,探测并求解组合观测值的周跳,然后还原求解原始信号的周跳值,最后通过实验验证这种方法的可行性。
这种方法优点十分明显:只需要得到三频观测值,形成超宽巷、宽巷和窄巷组合,在历元间差分即可,而且具有动态性、实时性,适用于动态、非差情况下的周跳探测。
传统的三频无几何相位组合,探测精度高,不受伪距噪声影响,但是只能形成两个线性无关的无几何相位组合观测量。既存在一些不敏感周跳,周跳修复又需要使用伪距测量来搜索,程序也不易实现。本文的优势在于超宽巷组合是伪距相位组合观测量,可以形成三个线性无关的组合观测量,对电离层延迟作了相关处理,不存在不敏感周跳组合,方法简单,程序也易于实现,探测精度比较高。
[1] 肖国锐,隋立芬,甘雨,戚国宾.北斗三频数据实时周跳探测与修复方法对比分析[J].测绘科学技术学报,2014,31(5):467-472.
[2] 李金龙,杨元喜,徐军毅,何海波,郭海荣.基于伪距相位组合实时探测与修复GNSS三频非差观测数据周跳[J].测绘学报,2011,40(6):717-729.
[3] 李征航,黄劲松.GPS测量与数据处理[M].武汉:武汉大学出版社,2012:141-143.
[4] 黄令勇,宋力杰,王琰,智遂强.北斗三频无几何相位组合周跳探测与修复[J].测绘学报,2012,41(5):763-768.
[5] 孙保琪,欧吉坤,等.一种适用于Compass周跳探测的三频数据优化组合[J].测绘学报,2012,41(5):585-588.
[6] 罗腾,白征东,原波.北斗三频组合数据在周跳探测和修复上的应用[J].测绘科学,2011,36(6):167-168.
[7] 胡加星.GPS三频数据探测与修复周跳的研究及应用[D].桂林:桂林理工大学,2012.
[8] 李金龙.GNSS三频精密定位数据处理方法研究[D].郑州:解放军信息工程大学,2011.
[9] Li B F,Feng Y M,Shen Y Z.Three carrier ambiguity resolution:distance-independent performance demonstrated using semi-generated triple frequency GPS signals[J]. GPS Solut,2010,14:177-184.
[10] Zhao Q L,Sun W B,Dai Z Q,et al.Real-time detection and repair of cycle slips in triple-frequency GNSS measurements[J].GPS Solut,2014.
Cycle Slip Detection and Repair Algorithms for BeiDou Triple Frequency Data
XIE Lan-tian,ZHAO Le-wen,YE Shi-rong
(Research Center of GNSS,Wuhan University,Wuhan 430079,China)
Carrier phase observations have been increasingly applied to the augmentation systems.Due to influence of the observational enviconment,carrier phase measurements will inevitably contain cycle slips.The cycle slips detection and repair is an important factor to improve the positioning accuracy.For BeiDou satellite,this paper presents a method with triple-frequency analyzing the characteristics of its different linear combination of observations,choosing the appropriate coefficient,forming a pseudo-phase combined observations and the two geometric free phase composition to detect cycle slips of the linear combination by the epoch difference and restores the original signal,and finally does experiments are carried out to validate the feasibility of this approach.
BeiDou satellite navigation and positioning system;Triple frequency;Cycle slips;Pseudo-range phase combination;Geometry-free phase combination
2015 - 07 - 15;
2015 - 07 - 30。
谢兰天(1993 - ),男,硕士,主要从事GNSS精密数据处理方面研究。
E-mail:272520580@qq.com
P228.41
A
2095-8110(2015)05-0037-07
