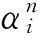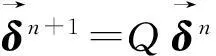非线性Schrödinger方程的五次B-样条逼近
2015-03-09梁宗旗
谢 烨,梁宗旗
(集美大学理学院,福建 厦门 361021)
非线性Schrödinger方程的五次B-样条逼近
谢烨,梁宗旗
(集美大学理学院,福建 厦门 361021)
[摘要]利用五次B-样条配点有限元方法研究了经典的三次非线性Schrödinger方程.在该格式中,关于时间方向的离散是基于Crank-Nicolson差分格式,而空间方向采用了分片五次B-样条函数逼近,其得到的刚度矩阵是一个分块五对角型矩阵.同时,利用线性稳定性分析方法证明了该格式是无条件稳定的.通过数值例子,验证了该格式保持了方程的守恒性质及具有较高的精度,最后模拟了两个孤立子的碰撞.
[关键词]非线性Schrödinger方程;B-样条;数值逼近;孤立子
0引言
非线性Schrödinger方程是一种典型的色散波动方程[1],这类方程从数学角度揭示了线性色散与非线性的交互作用,同时也是研究光孤子特性的基本方程.等离子体的Langmuir波、一维色散的自调制、二维定态平面波的自聚焦、超导电子对电磁场中的运动等都可以用非线性Schrödinger方程来描述.非线性Schrödinger方程不仅具有无穷个守恒律,存在Backlund变换和完全可积等特性,同时利用散射反演法和修正映射等方法得到了该方程及带有克尔效应的非线性Schrödinger的精确解及其孤立子解[2-7].为了考察孤立子的稳定性和相互作用,一大批非线性进化方程的数值计算方法也随之应运而生,因为是否保持原方程的守恒性和孤立子碰撞及是否改变其形态可以作为衡量和检验数值方法好坏的一个重要标尺.
本文研究如下的三次非线性Schrödinger方程的Dirichlet初边值问题:
(1)
其中:u(x,t) 是未知复值函数;ut=∂u/∂t;uxx=∂2u/∂x2;u0(x)是已知函数;i2=-1;q为实常数,如果q<0 称为散焦,q>0称为聚焦.设u(x,t)及其导数在x→±时指数衰减为0,则方程的解满足如下的守恒律[1]:
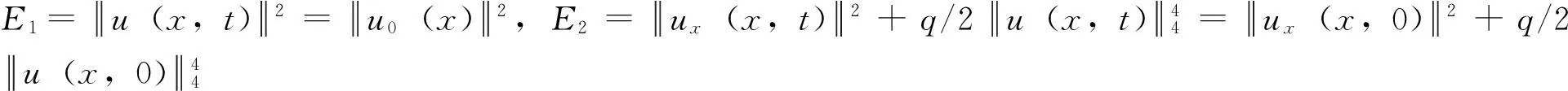
(2)

近几十年来,许多学者对非线性Schrödinger方程在数值计算方法中的应用进行了广泛的研究:Delfour等人[8]提出了一个有限差分格式;Taha等人[9]总结和提出了5个有限差分格式和2种Fourier分裂法和拟谱方法;Sanz-Serna[10]提出了“蛙跳格式”和改进的Crank-Nicolson格式,并用半离散的方法讨论了守恒和不守恒的格式[11].关于该方程有大量的数值方法研究文献,如谱方法[12]、拟谱方法[13]、有限元方法[14]、有限差分方法[15-16]、多辛格式[17]等等.近年来Bao等[18]利用分裂Hermite及Legurrer谱方法在研究非线性Schrödinger方程以及更广泛的Gross-Pitaevskii方程和Bose-Einstein 凝聚态方程方面取得了突破性的进展.
B-样条是样条曲线一种特殊的表示形式,由于其具有很好的支撑性、灵活性和光滑性,被广泛应用于计算几何中.B-样条是贝兹曲线[19]的一种一般化,可以进一步推广为非均匀有理B样条(NURBS),使得能给更多一般的几何体建造精确的模型.自从石钟慈[20]基于均匀分划的B样条展开定理构造三次B样条基函数来表示位移场函数和应用最小势能原理导出样条有限元以来,以三次和五次B-样条基函数为逼近函数的计算方法得到了极大的发展,如:应用四、五、七次B-样条方法求解Korteweg-de Vries-Burgers(KdVB)方程[21-23];应用五次B-样条求解混合 Korteweg-de Vrie(CMKdV)方程的数值解[24].本文拟通过在空间方向采用五次B-样条离散,时间方向采用Crank-Nicolson 差分格式离散的方法来求解非线性Schrödinger方程的数值解,通过Matlab来实现数值解的计算.
1五次B-样条法
1.1 五次B-样条的构建
问题(1)是定义在无界区域上的,一般有3种方法求解无界区域问题:1)截取有限区间,加入人工边界条件;2)利用Hermite谱方法或Lagurrer谱方法;3)通过映射将无界区域变为有界区域,再利用有界区域的Legendre多项式或有理多项式逼近.
本文采用第一种方法,即将问题(1)转化为有限区间[a,b]上初边值问题,其中a,b的选择取决有u(x,t)的衰减情况.这样原方程的Dirichlet初边值问题变为如下的问题:
(3)
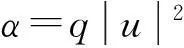
(4)
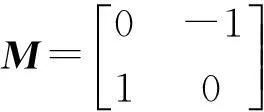
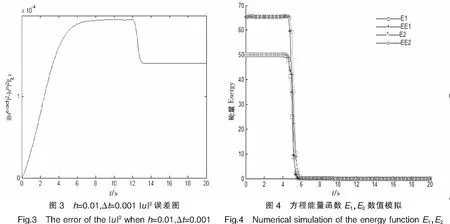
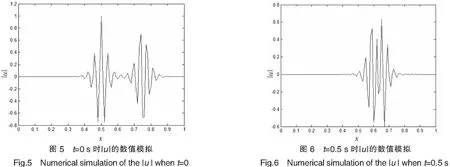
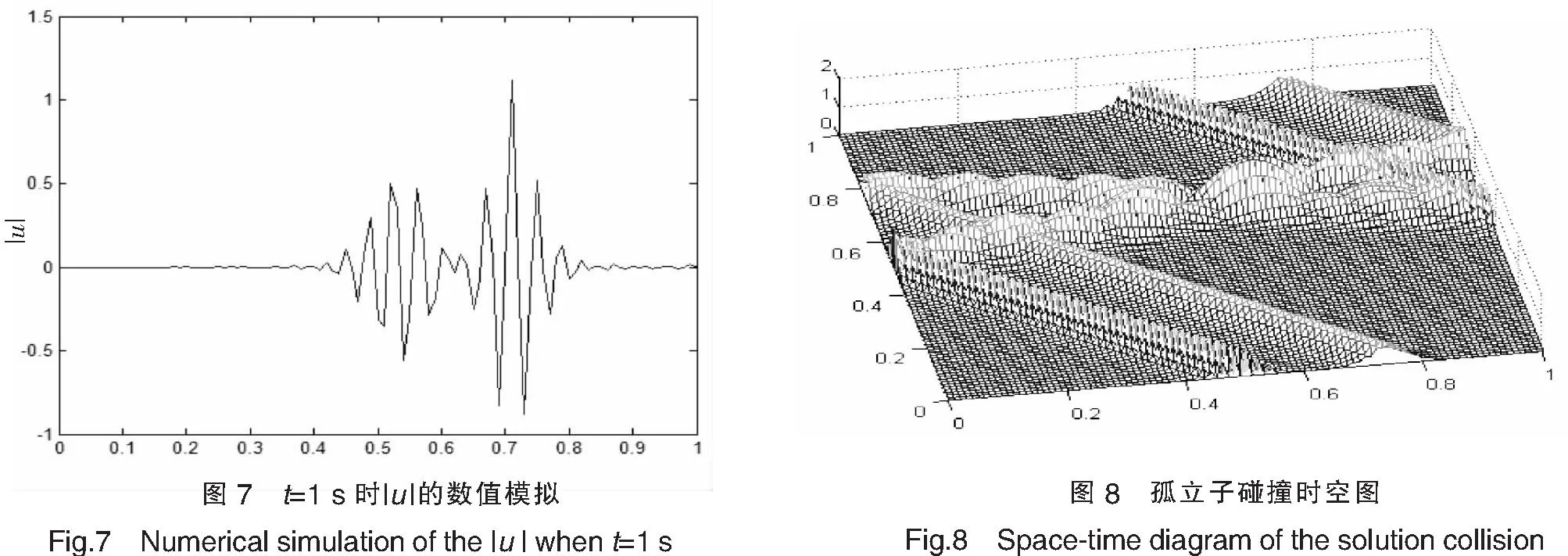
本文将区间[a,b]等分为N个有限单元,步长h=(b-a)/N,节点为xi,a=x0 (5) 其中h=xi+1-xi,i=-2,-1,…,N+2. (6) 令η=(x-xi)/h,其中0≤η≤1,代入式(5)得: (7) (8) 式(7)代入方程(6)中得: (9) 其中:αi=q(vi2+wi2)=q[(Reδi-2+26Reδi-1+66Reδi+26Reδi+1+Reδi+2)2+(Imδi-2+26Imδi-1+66Imδi+26Imδi+1+Imδi+2)2],i=0,1,2,…,N. 用Crank-Nicolson方法,得: (10) 将式(10)代入方程(9)得: (11) 容易验证式(11)满足守恒律: (12) (13) 式(11)是全隐格式,为了避免求解非线性方程组,对非线性项进行处理,利用Taylor展开式: 经过这样处理后的方程组(11)变为一个线性方程组,更利于计算. (14) (15) k1=I/Δt+10M/h2-αM/2,k2=26I/Δt+20M/h2-13αM,k3=66I/Δt-60M/h2-33αM,k1=k4,k2=k5, d1=I/Δt-10M/h2+αM,d2=26I/Δt-20Μ/h2+13αM,d3=66I/Δt+60M/h2+33αM,d1=d4,d2=d5, 从而得到如下的矩阵方程组:A0δ0=B0.其中: 2稳定性分析 假设(11)的解的形式是: (16) 将式(16)代入式(11)得: 根据Von Neumann稳定性分析,说明本文所提供的格式是无条件稳定的,这也意味着该格式对步长h和Δt没有任何限制,但在实际计算中应选择适当小的网格,保证不降低精度. 3数值例子 例1为了便于比较和简单起见,取文献[7]中的例子: 该方程的精确的孤波解为:u(x,t)=sech(x-4t)exp[2ix-3it].定义如下的L2误差来度量数值解un和精确解uexact在每一时间层上的误差: 取时间步长和空间步长h=0.01,Δt=0.001,图1—图3分别画出了ReL2、ImL2及模L2在时间t=20s时的误差图.从中可以看出,随着时间的增加,实部误差、虚部误差和模误差,在大约t∈[0,6]时误差是递增的,但当t≥6s之后,误差将会在一个较小的但稳定的区域震荡,之后基本保持不变或递减,说明该格式有较好的稳定性和较好的精度.图4给出的原方程关于能量函数E1,E2守恒律的验证,其中E1,E2分别表示精确解(2)的能量函数,EE1,EE2表示数值解(12),(13)的计算值.从图4可以看出,格式较好地保持了原方程的守恒律. 本文构造的计算方法是一种简单、有效、具守恒性、有较高精度的格式. 例2设方程 其精确解是:u(x,t)=e-2ix-3itsech(x-10+4t)+e2ix-3itsech(x-4t).该方程具有孤立子碰撞的现象,用五次B-样条数值方法模拟了两个孤立解碰撞模型. 从图5—图7中可以看出,两个孤立子在t=0s两个孤立子保持各自的振幅和频率相向运动,当t=0.5s时,两个孤立子发生碰撞,当t=1s时,碰撞后两个孤立子基本保持原有振幅和频率相背运动.它的时空图见图8.孤立子碰撞是该方程最具特征的性质,本文的数值计算很好地模拟了这一现象. 4结论 本文主要运用五次B-样条配置方法求非线性Schrödinger方程的数值解,构造了一个时间具二阶精度、空间方向具四阶精度的计算格式.该格式的主要特点是在空间方向的离散采用了五次B-样条方法,这样的格式是一个全隐格式,对应的将需要求解一个非线性方程组.为克服这一缺点,对非线性项,利用Taylor展开,将原非线性方程组求解问题降解为只需求解一个分块五对角型的一个线性方程组,这样大大减低了计算量和计算复杂度,同时证明了该格式是无条件稳定的.最后通过数值结果,验证了该格式的稳定性、守恒性、精度等. [参考文献] [1]SULEM C,SULEM P L.The nonlinear Schrödinger equation-self-focusing and wave collapse[M].New York:Springer,1999. [2]ZHANG Z Y,LIU Z H.New exact solutions to the perturbed nonlinear Schrödinger’s equation with Kerr law nonlinearity[J].Appl Math Comput,2010,216:3064-3072. [3]ZHANG Z Y,LI Y X,LIU Z H.New exact solutions to the perturbed nonlinear Schrödinger’s equation with Kerr law nonlinearity via modified trigonometric function series method[J].Communications in Nonlinear Science and Numerical Simulation,2011,16(8):3097-3106. [4]ZHANG Z Y,LIU Z H,MIAO X J,et al.Qualitative analysis and traveling wave solutions for the perturbed nonlinear Schrödinger’s equation with Kerr law nonlinearity[J].Physics Letters A,2011,375:1275-1280. [5]ZHANG Z Y,GAN X Y,YU D M.Bifurcation behaviour of the travelling wave solutions of the perturbed nonlinear Schrödinger equation with kerr law nonlinearity[J].Zeitschrif fur Naturforschung A,2011,66:721-727. [6]ZHANG Z Y,GAN X Y,YU D M,et al.A note on exact traveling wave solutions of the perturbed nonlinear schrödingers equation with kerr law nonlinearity[J].Commun Theor Phys,2012,57:764-770. [7]ZHANG Z Y,HUANG J H,ZHONG J,et al.The extended (G ’/G)-expansion method and travelling wave solutions for the perturbed nonlinear Schrödinger’s equation with Kerr law nonlinearity[J].Pramana-Journal of Physics,2014,82(6):1011-1029. [8]DEFLOUR M,FORTIN M,PAYRE G.Finite-difference solution of nonlinear Schrödinger equation[J].Comput Phys,1981,44:277-288. [9]TAHAAND T R,ABLOWITA M J.Analytical and numerical aspects of certain nonlinear evolution equations II:numerical nonlinear Schrödinger equation[J].J Comput Phys,1984,55:203-230. [10]SANZ-SERNA J M.Methods for the numerical solution of the nonlinear Schrödinger equation[J].Math Comput,1984,43(167):21-27. [11]SANZ-SERNA J M,VERWER J G.Conservative and nonconser vative schemes for the solution of the nonlinear Schrödinger equation[J].IMA J Numer Anal,1986,6:24- 42. [12]WANG H Q.An efficient Chebyshev-Tau spectral method for Ginzburg-Landau-Schrödinger equations[J].Computer Physics Communications,2010,181:325-340. [13]JAVIDI M.A Golbab numerical studies on nonlinear Schrödinger equations by spectral collocation method with preconditioning[J].Math Anal Appl,2007,333:1119-1127. [14]LI W.Two-grid mixed finite-element methods for nonlinear Schrödinger equations[J].Numerical Methods for Partial Differential Equations,2012,28(1):63-73. [15]WANG T C.Maximum norm error bound of a linearized difference scheme for a coupled nonlinear Schroinger equations[J].Journal of Computational and Applied Mathematics,2011,235:4237- 4250. [16]CHANG Q ,JIA E,SUN W.Difference schemes for solving the generalized nonlinear Schrödinger equation[J].Comput Phys,1999,148:397- 415. [17]徐金平,单双荣.带五次项的非线性Schrödinger方程的多辛Fourier拟谱算法[J].数值计算与计算机应用,2010,31(1):55-64. [18]BAO W Z ,LI H L,JIESHEN.A generalized Laguerre-Fourier-Hermite pseudospectral method for computing the dynamics of rotating in Bose-Einstein condensates[J].SIAM J Sci Comput,2009,31:3685-3711. [19]PRENTER P M.Splines and variational methods[M].New York:John Wiley & Sons,1975:58-69. [20]石钟慈.样条有限元[J].计算数学,1979,1(1):50-72. [21]BULENT SAKA,IDRIS DAG.Quartic B-spline Galerkin approach to the numerical solution of the KdVB equation[J].Applied Mathematics and Computation,2009,215:746-758. [22]ZAKI S I.A quintic B-spline finite elements scheme for the KdVB equation[J].Comput Methods Appl Mech Engrg,2000,188:121-134. [23]TALAAT S,ALY EL-DANAF.Septic B-spline method of the Korteweg-de-Vries-Burger’s equation[J].Communications in Nonlinear Science and Numerical Simulation,2008,13:554-566. [24]ISMAIL M S.Numerical solution of complex modified Korteweg-de Vries equation by collocation method[J].Communications in Nonlinear Science and Numerical Simulation,2009,14:749-759. (责任编辑马建华英文审校黄振坤) Numerical Approach of the Nonlinear SchrödingerEquation by the Quintic B-SplineXIE Ye,LIANG Zong-qi (School of Science,Jimei University,Xiamen 361021,China) Abstract:In this paper,the quintic B-spline collocation finite element method is implemented to find numerical solution of the classic cubic nonlinear Schrödinger equation.The scheme is based on the Crank-Nicolson formulation for time discretization and quintic B-spline functions for space discretization,and the stiffness matrix of the scheme is a block-five-diagonal matrix.The scheme is verified to be unconditionally stable by the method of linear stability analysis.By numerical examples,it is confirmed that the scheme keeps the conservative property of the equation preferably.Finally,the collision of two solitons is simulated. Key words:nonlinear Schrödinger equation;B-spline;numerical approach;soliton [中图分类号]O 241.82 [文献标志码]A [文章编号]1007-7405(2015)02-0145-09 [作者简介]谢烨 (1989—),女,硕士生,从事计算数学方向研究.通讯作者:梁宗旗 (1964—),男,教授,硕导,从事计算数学方向研究,E-mail:zqliang@jmu.edu.cn. [基金项目]福建省自然科学基金资助项目(2012J01013);福建省高校科研专项基金资助项目(JK2012025);福建省科技厅重点课题(2014H0034) [收稿日期]2014-05-15[修回日期] 2014-10-12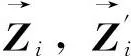
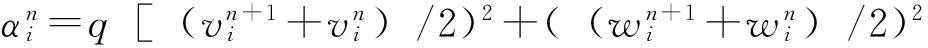


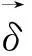
1.2 初值问题的处理