STLFM在水声通信系统同步测算中的应用

黄娜娜，郑佳春，雷　洪

(1.集美大学航海学院，福建 厦门 361021；2.集美大学信息工程学院，福建 厦门 361021)



STLFM在水声通信系统同步测算中的应用

黄娜娜1，郑佳春2，雷洪1

(1.集美大学航海学院，福建 厦门 361021；2.集美大学信息工程学院，福建 厦门 361021)

[摘要]通过对对称三角线性调频(STLFM)信号在分数阶傅里叶域能量汇聚性的分析，提出了采用STLFM信号作为同步码，基于分数阶Fourier变换(FRFT)的正交多载波水声通信系统的联合同步算法，并以同步误码率(BER)作为评价指标，在有噪声、多径传输和多普勒效应三种环境组合下与传统OFDM系统采用线性调频(LFM)信号作为同步码进行仿真分析比较.仿真结果表明，在复杂的水声环境中，该算法在低信噪比时可以获得更精确的同步性能和更低的误码率.

[关键词]水声通信；正交频分复用；分数阶傅里叶变换；对称三角线性调频信号；联合同步

0引言

水声通信(Under Water Acoustic Communication,UWA Communication)是实现水下综合信息感知与交互的主要手段.水声信道是水下唯一可以进行远距离信息传输的物理媒质，不同于无线电信道，声信道被看作缓慢时变的相干多途信道[1]，是时间弥散的慢衰落信道，能量损失不仅随距离并且随频率增加而变大，因此其可用带宽只有几千赫兹.水声信道信息容量小，传播过程中时变、空变及多途效应严重，这些都严重制约着水声通信技术的发展.多载波正交频分复用(Orthogonal Frequency Division Multiplexing,OFDM)凭借其结构简单，频谱利用率高和抗频率选择性衰落的特点，成为高速水声通信最常用的技术手段[2-5].但由于其对频偏和相位噪声非常敏感，仅1%的频偏就能使信噪比(SNR)下降30 dB，所以OFDM的同步成为水声通信系统必须要解决的关键问题之一[6-11].

常用的符号同步方法有Takahashi法[6]和Ramasubramanian法[7]，但这两种方法对载波频偏很敏感，精度不高.文献[8-9]方法需要的信道信息较少，但运算量过大；文献[10-11]方法克服了运算复杂度，但估计精度还有待提高.文献[12]提出了基于时域相关法的定时同步方案，采用LFM或者HFM导频同步信号进行定时同步和多普勒估计与补偿，实现了10-3量级的定时同步，同步方法简单.文献[13]研究了以LFM信号和带循环前缀的OFDM符号作为帧同步前导符号的两种帧同步体制的性能，得出LFM信号在小信噪比时有效且实现同步，而OFDM循环前缀体制只在大信噪比时可用.文献[14]提出在分数阶傅里叶域搜索由插入到OFDM符号中LFM信号所产生的对称点的位置，实现联合同步，但同步误码率较高.

本文采用的同步方法是基于对称三角线性调频(STLFM)信号在分数阶傅里叶域能量汇聚性的分析[15]，针对OFDM系统需解决的同步问题，提出了采用STLFM信号作为同步码，基于分数阶Fourier变换(FRFT)的正交多载波水声通信系统的同步检测整体方案.

1算法模型

1.1　STLFM信号的FRFT分析

设STLFM信号的复解析信号模型为：

(1)

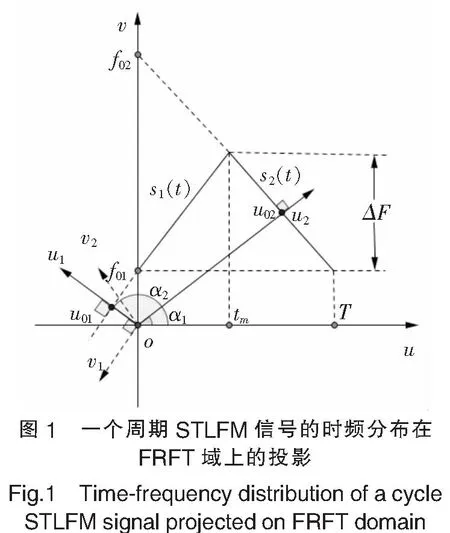
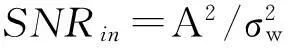
由于FRFT可以理解为角α的时频旋转，根据该特点，可以分析STLFM信号在FRFT域的频谱分布特性.信号的量纲归一化采用文献[17]提出的离散尺度变换法.以一个信号周期为观察时间，如图1所示为一个调制周期的STLFM信号的时频分布及其在FRFT域的投影.α1、α2分别为一个信号周期中包含的两段LFM信号的“最佳”分数阶旋转角，在其对应的FRFT域内，STLFM信号呈现能量尖峰，u01、u02分别为两段LFM信号的尖峰u坐标值.

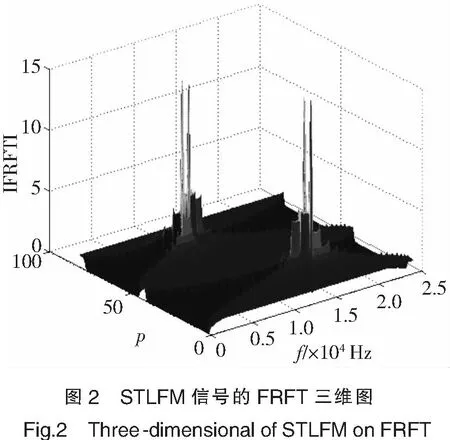
如图2所示，以一段包含一个调制周期的STLFM信号为例，仿真分析其频谱幅度在FRFT域的分布特征.设信号的各个参数分别为fc=5kHz，ΔF=4 kHz，Fs=48kHz，tm=0.25 s.由图2可以看出，STLFM信号在平面(u,α)上形成4个高度相近的能量尖峰，即在p1阶、p2阶处分别出现两个能量尖峰.因此，当采用STLFM信号作为同步码，在接收端通过检测这些尖峰可以实现精确的辨识，信号识别力大大提高.

1.2　联合同步算法

1.2.1FRFT-OFDM系统模型

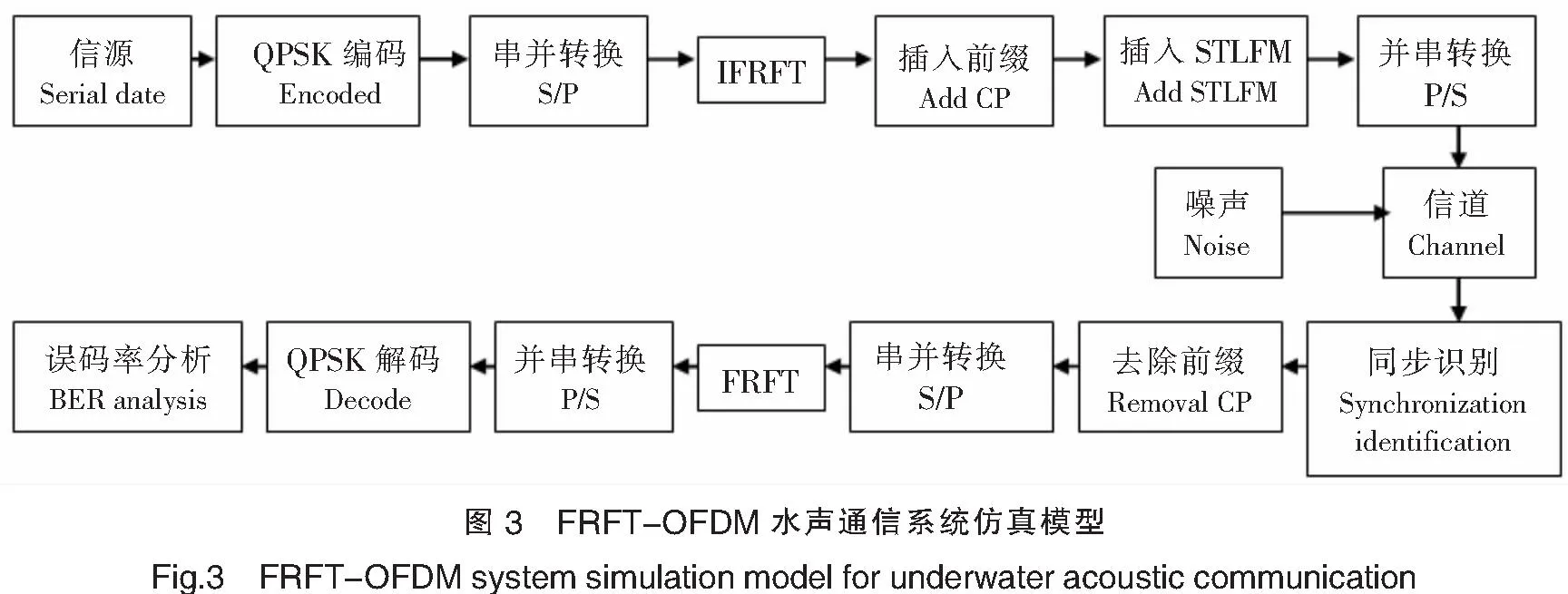
本文提出的 FRFT-OFDM水声通信系统模型如图3所示[18].在发送端，为降低码间干扰和对抗多径时延扩展，在每帧信号之间插入了循环前缀作为保护间隔，本系统模型与传统的OFDM系统的区别是在每帧信号之前加入STLFM信号作为同步码.而此时相对于传统的OFDM系统就增加了FRFT的长度，影响了传输速率，但获得了更为精确的同步性能.本文着重研究OFDM系统的同步性能，因此暂不考虑传输速率的影响.在接收端，首先进行了同步识别，即将信号接收后先串并转换，然后做分数阶傅里叶变换，检测出同步码的位置，完成同步识别.然后去除循环前缀，后续步骤与传统的OFDM系统相同，这里不再阐述.

1.2.2FRFT-OFDM信号模型

设Ts为发射端采样周期，N为子载波个数，根据FRFT-OFDM信号的采样原理[14]，发送信号y(k)可表示为

(2)

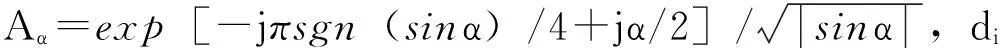
设Δfc为接收端载波频差，Δfs为接收端采样频差，Tr=N/(N/Ts-Δfs)为接收端采样周期，h(k)为信道冲激响应，η(k)为噪声向量，则接收信号表示为：

(3)

1.2.3FRFT-OFDM联合同步方法

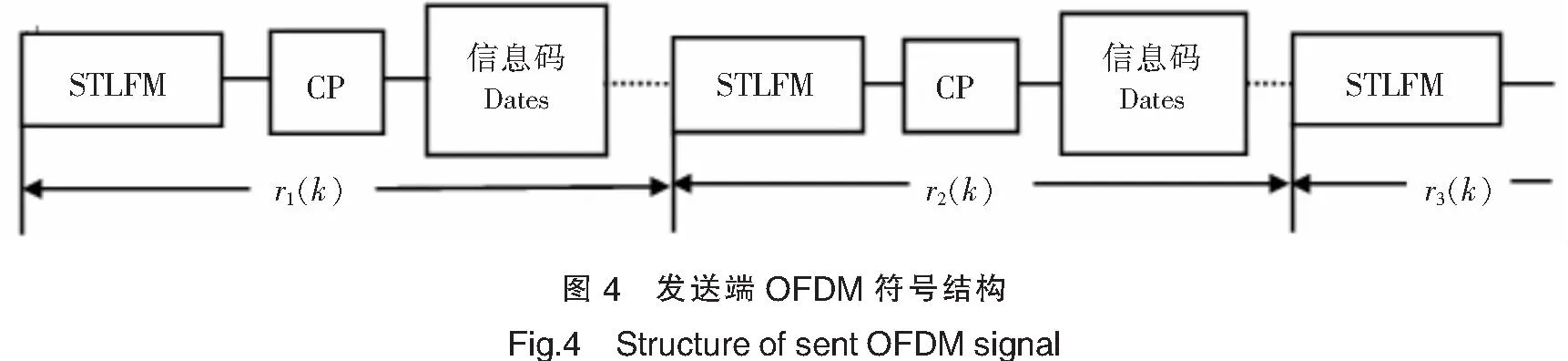
发送端同步信号的生成采用在每段循环前缀之前加入一段长度为NL的STLFM信号作为同步码，并由一条独立的子载波进行传输.以TL=2tm为周期对STLFM信号L(t)进行采样得到长为NL的序列Li(k)，其中，Ns为一个OFDM符号的长度，由STLFM信号、CP与有用数据组成.发送端OFDM符号结构如图4所示.

1.2.4同步参数估计

随机截取长为3Ns的一段接收信号，并检测出其中传输STLFM信号的3条子载波，设L1(k)由第0条子载波传输，可知L2(k)、L3(k)分别由第N条、第(N-1)条子载波传输，以上截取的接收信号是由3段长度均为Ns的r1(k)、r2(k)、r3(k)构成，并可表示为

(4)

其中rL(k)、rcp(k)、rs(k)分别表示STLFM信号、CP及有用数据的接收信号.考虑传输3段STLFM信号的子载波位置，结合式(2)、式(3)，设k0为符号定时参数，可将rL1(k) 表示为

(5)

由STLFM信号的FRFT分析可知，当p1=-2arccotu1/π，p1=-2arccotu2/π时，STLFM信号呈现能量尖峰.本文参考了文献[19]，调频斜率k与“最佳”分数阶p有确定的对应关系，k=-cot(2p/π)，当参数调频斜率k取值确定时，“最佳”分数阶p也就唯一确定了.因此，先对r1(k)分别作p1阶、p2阶FRFT，可得

(6)

(7)

在式(6)、式(7)中都只有第2项含有STLFM信号L(k)，从而在p1阶、p2阶处均会出现能量尖峰，此时可忽略其他项.

又根据FRFT线性特性可知：

(8)

(9)

从式(8)、式(9)可以看出，在p1阶处只有L1(k)会产生能量尖峰，在p2阶处只有L2(k)会产生能量尖峰，因此，一个周期的STLFM信号分别在p1阶、p2阶处作FRFT，各能产生一次能量尖峰，大大提高了目标分辨率，为实现同步提供了良好的条件.

首先分析STLFM信号在p1阶处的FRFT，此时对应的旋转角为α1，对于式(8)的第二项有：

(10)

其中，hl(k)、τl表示L个传播路径中第l条径的信道冲击响应与时延.

根据卷积定理，式(10)中，令：Dα=-π{Ts/[(N-TsΔfs)TL]}2cotα1，f(k)=1，g(k)=exp{j2π(kTL)[ΔfcTr/TL+(k0+τl)Ts2/(N-TsΔfs)2cotα1]}L1[k-(k0+τl)]，而

(11)

由FRFT的时移特性和相移特性可得：

(12)

其中，θ1=ΔfcTr/TL+(k0+τl)Ts2/(N-TsΔfs)2TLcotα1.因此，结合分数阶卷积的性质和卷积定理，可将式(10)表示为

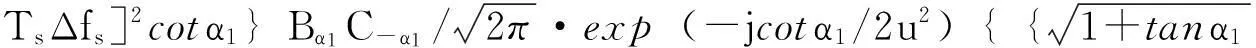
tanα1)]}*{Ap1σ[u-(k0+τl)cosα1-θ1sinα1]·exp{jπ{[(k0+τl)2-

θ12]sinα1cosα1-2u[(k0+τl)sinα1-θ1cosα1]}+jcotα1/2u2}}}，

(13)

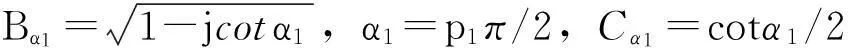
由式(13)可以看出，卷积的第二项含有冲激函数，因此会出现冲激响应.由于存在多径传播，卷积结果中将会出现多个冲激响应点，搜索第一个冲激响应点，对于多径信道的第1径，则其时延τ0=0，记其位置为a1：

a1=k0cosα1+[ΔfcNTs/(N-TsΔfs)TL+k0Ts2cotα1/(N-TsΔfs)2TL]sinα1，

(14)

同理可得

a2=k0cosβ1+[ΔfcNTs/(N-TsΔfs)TL+k0Ts2cotβ1/(N-TsΔfs)2TL+

Ncscβ1/(N-TsΔfs)TL]sinβ1，

(15)

a3=k0cosγ1+[ΔfcNTs/(N-TsΔfs)TL+k0Ts2cotγ1/(N-TsΔfs)2TL+

(16)

联立式(14)、(15)、(16)，解得：

(17)

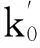
同理可分析STLFM信号在p2阶处的FRFT，此时对应的旋转角为α2：

(18)

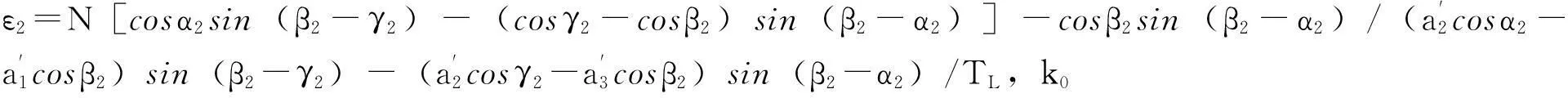
至此，STLFM信号在p1阶和p2阶处的采样频率Δfs估计、载波频率Δfc估计和符号定时k0估计已经完成.由于STLFM信号可以在p1阶和p2阶两处作FRFT而得到两次参数估计，所以与传统的采用LFM信号作为同步码而只能作一次的参数估计相比，具有更高的可靠性.

2仿真分析

系统采用QPSK调制方式，仿真参数为：水声信道带宽为5 kHz，采样频率为48 kHz,FRFT长度为256，循环前缀长度为64，每帧中OFDM符号个数为10，水声信道径数为5，多普勒频移相对速度为10 m/s.

图5—图7是本文提出的采用STLFM信号作为同步码与传统采用LFM信号作为同步码的OFDM系统分别在存在噪声、噪声与多径、噪声多径与多普勒频移三种水声环境时，数据传输误比特率(BER)对比图.由图5可知，在水声环境只有噪声的情况下，系统误码率性能基本相同；由图6可知，在存在噪声和多径传输两种干扰的水声环境时，对于小信噪比时，采用STLFM信号作为同步码的系统误码率更小，大信噪比时效果更为显著；由图7可知，在水声环境同时存在噪声、多径传输和多普勒效应时，采用STLFM信号作为同步码在整体上比采用LFM信号作为同步码能获得误更小的误码率.

综上所述，STLFM信号作为同步码具有优越性如下：1)STLFM信号在作FRFT时，会形成4个尖峰，搜索尖峰，能实现同步识别.2)利用STLFM信号能在两处进行参数估计，可以通过求平均值等方法提高参数估计的可靠性.3)以误码率为评价指标，采用STLFM信号作为同步码比采用LFM信号作为同步码系统的误码率更低，而对于水声环境复杂的系统，在低信噪比时采用STLFM信号作为同步码具有明显的优越性.本文主要以误码率作为评价标准来进行同步性能的探讨，而对于捕获概率，以及虚警、漏警概率的探讨，将在后续研究中进行.

3结论

本文根据STLFM信号包含的各段LFM信号在其对应的“最佳”分数阶域内具有很好的能量聚集性，提出了一种基于分数阶Fourier变换以STLFM信号作为同步码的正交多载波水声通信的联合同步算法方案.与其他传统的采用单一LFM信号作为同步码相比，检测分辨率大大提高，改善了系统性能.通过计算机仿真，得出结论，采用STLFM信号作为同步码比采用LFM信号作为同步码可以获得更好的误码率等性能，对于水声环境复杂的系统，在低信噪比时采用STLFM信号作为同步码具有明显的优越性.该算法较其他传统算法表现出较大的优势，具有一定的理论和实用价值.

[参考文献]

[1]殷敬伟.水声通信原理及信号处理技术[M].北京：国防工业出版社，2011.

[2]KISHORE C N,REDDY V U.A technique for dominant path delay estimation in an OFDM system and its application to frame synchronization in OFDM mode of WMAN[J].EURASIP Journal on Wireless Communications and Networking,2006(2):18-25.

[3]KANG T,ILTIS R A.Iterative carrier frequency offset and channel estimation for underwater acoustic OFDM systems[J].IEEE Journal on Selected Areas in Communications，2008，26(9):1650-1661.

[4]GREERT L,PAUL A W.Multiband OFDM for covert acoustic communications[J].IEEE Journal on Selected Areas in Communications,2008,26(9):1662-1673.

[5]RUGINI L,BANELLI P，LEUS G.Simple equalization of time-varying channels for OFDM[J].IEEE Communication Letters,2005,9(7):619-621.

[6]TAKAHASHI K,SABA T.A novel symbol synchronization algorithm with reduced influence of ISI for OFDM systems[C]//IEEE GLOBECOM.San Antonio,Texas,USA：IEEE，2001:524-528.

[7]RAMASUBRAMANINA K,BAUM K.An OFDM timing recovery scheme with inherent delay-spread estimation[C]//IEEE GLOBECOM.San Antonio,Texas,USA：IEEE,2001:3111-3115.

[8]FUSCO T,TANDA M.Blind synchronization for OFDM systems in multiple channels[J].IEEE Trans on Wireless Communications,2009,8(3):1340-1348.

[9]LAOURINE A,STEPHENE A,AFFES S.Blind sampling clock offset estimation in OFDM system based on second order statistics[C]//Fortieth Asilomar Conference，Signals，Systems and Computer,CA:Pacific Grove,2006:1782-1785.

[10]胡登鹏,石峰,张尔杨.非数据辅助的OFDM系统联合同步算法的设计[J].系统工程与电子技术,2011,33(1):183-189.

[11]胡登鹏,张尔杨.非数据辅助的OFDM系统采样频率同步算法[J].信号处理,2010,26(6):956-960.

[12]郑佳春,邵进兴.多载波水声通信系统的定时同步研究[J].中国航海,2012,35(3):27-30.

[13]吕丹丹,杨士莪.水声多载波通信系统帧同步技术试验研究[J].声学技术,2012,31(4):270-275.

[14]申勇,达新宇,曾武.FRFT-OFDM系统联合同步算法[J].中国科学院研究生院学报,2012,29(5):714-719.

[15]袁伟明,王敏,吴顺君.对称三角线性调频连续波信号的检测与参数估计[J].电波科学学报,2005,20(5)：594-597.

[16]张容权,杨建宇,熊金涛，等.对称三角线性调频连续波信号模糊函数分析[J].电子学报,2004,32(3):353-356.

[17]赵兴浩,邓兵,陶然.分数阶傅里叶变换数值计算中的量纲归一化[J].北京理工大学学报,2005,25(4):360-364.

[18]王逸林,陈韵,殷敬伟，等.基于分数阶Fourier变换的正交多载波水声通信系统研究[J].通信学报,2012,33(8):162-170.

[19]殷敬伟,惠俊英,蔡平,等.基于分数阶Fourier变换的水声信道参数估计[J].系统工程与电子技术,2007,29(10):1624-1627.

(责任编辑朱雪莲英文审校黄振坤)

A Novel and Precise Synchronization Detection Algorithm inMobile Underwater Acoustic Communication SystemHUANG Na-na1，ZHENG Jia-chun2,LEI Hong1

(1.Navigation Institute，Jimei University,Xiamen 361021,China;

2.School of Information Engineering，Jimei University,Xiamen 361021,China)

Abstract:By analyzing the symmetrical triangular linear frequency modulation (STLFM) signal has convergence of energy in the FRFT，the paper proposed using STLFM signal as the preamble to achieve orthogonal Multi-carrier underwater acoustic communication system joint synchronization algorithm with fractional Fourier transform (FRFT).Using bit error rate (BER) as the evaluation index，simulation analysis this algorithm and comparison with traditional OFDM system using linear frequency modulation (LFM) signal as the preamble in the environment with noise，multipath propagation and Doppler effect.Simulation results show that the more complex environment of underwater acoustic systems，STLFM signals as preamble can obtain the more accurate synchronization performance and the lower error rate.

Key words:underwater acoustic communication;orthogonal frequency division multiplexing;fractional Fourier transform;symmetrical triangular linear frequency modulation signal;joint synchronization

[文献标志码]A

[中图分类号]TB 567

[文章编号]1007-7405(2015)02-0121-07

[作者简介]黄娜娜(1988—)，女，硕士生，从事分数阶傅里叶变换在水声通信中的应用研究.通讯作者：郑佳春(1965—)，男，副教授，从事通信与信息处理系统方向的研究，E-mail:jchzheng@jmu.edu.cn.

[基金项目]福建省自然科学基金项目(2013J01203)；福建省软科学项目(2013R0080)；交通部科技项目(2012-329-815-290)；厦门市科技计划项目(3502Z20130005)；李尚大集美大学学科建设基金(ZC2012013)

[收稿日期]2014-06-11[修回日期]2014-12-10