非理想边界拱的面内失稳模式与屈曲荷载*

康厚军，易壮鹏，曾有艺

(1.湖南大学 土木工程学院， 湖南 长沙 410082；2.长沙理工大学 土木与建筑学院, 湖南 长沙 410114)

非理想边界拱的面内失稳模式与屈曲荷载*

康厚军1，易壮鹏2†，曾有艺2

(1.湖南大学 土木工程学院， 湖南 长沙 410082；2.长沙理工大学 土木与建筑学院, 湖南 长沙 410114)

将拱结构中既非固结也非铰支的非理想边界考虑为沿不同方向的具有一定刚度的弹性约束，利用变形几何关系和能量变分原理推导了拱的非线性平衡方程.以圆弧拱为例建立了径向均布荷载下外荷载与结构内力、径向位移之间的关系，通过定义拱的深浅参数和临界约束刚度进行分析并得到了跳跃屈曲、分岔屈曲等的发生条件及存在区间.本文方法所得屈曲路径和屈曲荷载与有限元法所得结论吻合良好，且用数值法分析了不同约束刚度时的屈曲路径和临界荷载.结果表明,临界深浅参数和临界约束刚度对圆弧拱的屈曲模式及屈曲临界荷载影响显著.

屈曲；圆弧拱；非理想边界；分岔屈曲；变分原理

拱结构[1]在土木、机械和航天航空等领域应用广泛.拱作为一种基本结构构件具有优良的受力特性，其力学特性受到国内外学者[2-3]广泛关注.如周期激励下内共振[4-6]时的分岔和混沌特性，冲击荷载作用下弹性浅拱的跳跃屈曲[7]等.静力方面，近年来,Pi等[8-10]采用解析法与有限元法对各种荷载与边界条件下拱结构的非线性屈曲特性进行了深入系统的研究．卫星等[11]探讨了多种参数对拱结构考虑2阶效应时弹性屈曲特性的影响．程鹏和童根树[12]综述了径向均布荷载下圆弧拱的面内屈曲特性．郭彦林等[13]提出了压弯圆弧拱平面内稳定承载力的设计建议公式.

这些文献侧重于研究边界为理想固结或铰支时拱的力学性能.结构的复杂分析在很多情况下需考虑复杂边界，如：大跨系杆拱桥中系杆将两端连起来，系杆与竖向弹性支座、地基的作用可抽象为轴向、径向弹性约束；机械拱臂或曲臂与相邻结构弹性连接，共同受力，可将其考虑为弹性约束；弹性地基上的拱型结构在外荷载作用下边界考虑为弹性更加合理.本文以圆弧拱为例，将非理想边界考虑为径向、轴向弹性约束，通过能量变分原理[14]建立非线性平衡方程，得到外荷载与结构内力、位移的关系，并分析屈曲模式与结构重要参数的关系.

1 基本方程与稳定分析

1.1 变形几何关系

图1(a)所示圆弧坐标下的圆弧拱，径向均布荷载q增至一定程度时会发生分岔屈曲(图1(b))或跳跃屈曲(图1(c))，2Θ为展开角，R为半径，θ为角坐标，kvi,kwi(i=±Θ)分别为两端径向、轴向弹性约束刚度.屈曲前变形呈现非线性，求解屈曲荷载及变形时需考虑屈曲前非线性的影响.图1(a)中拱上任意一点P总的轴向应变εP=εm+εb，其中薄膜应变εm和弯曲应变εb分别为：

(1)

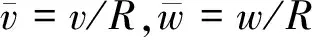
1.2 非线性平衡方程

圆弧拱在q作用下无量纲的总能量为：

(2)

轴向平衡方程：

(3)

图1 弹性约束非理想边界圆弧拱结构示意图

径向平衡方程：

(4)

轴向边界条件：

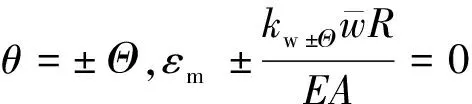
(5)

径向边界条件：

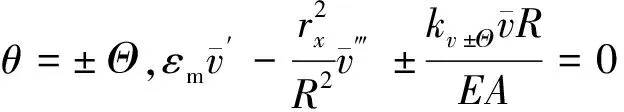
(6)

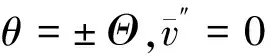
(7)

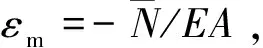
(8)

将式(8)代入式(4)并利用式(3)可得径向平衡微分方程为：

(9)

利用边界条件，由式(6)和式(7)可得径向位移表达式为:

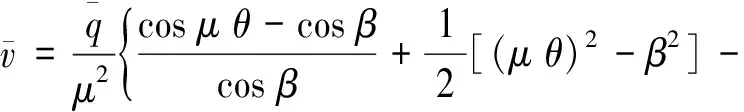
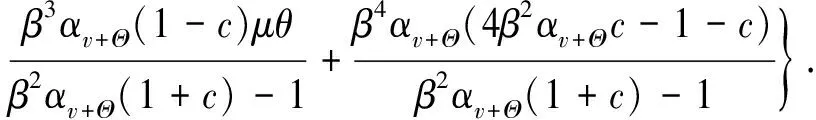
(10)

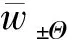
(11)

其中:

(12)

(13)

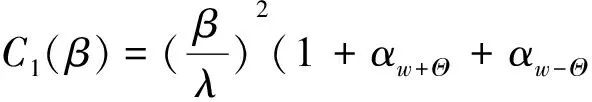
(14)

式中:αw±Θ=EA/(2kw±ΘRΘ)是单位长度轴向刚度EA/2RΘ与θ=±Θ处约束刚度kw±Θ的比值，可度量轴向约束的柔度;λ=RΘ2/rx是定义深浅程度的重要参数.式(11)建立了q和μ的函数关系.

1.3 跳跃屈曲分析

发生跳跃屈曲时，临界值位于极值点，所以在式(11)中发生屈曲的位置有dq/dμ=0，利用式(11)中q与μ的隐函数关系F(q,μ)=0可得:

(15)

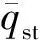
A2(β)=2A1(β)+D2(β),

B2(β)=4A1(β),

C2(β)=B1(β)-C1(β),

(16)

(17)

1.4 分岔屈曲分析

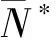
(18)

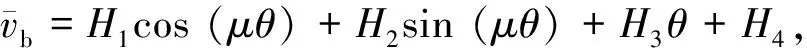
sinβcosβ[1-β2αv+Θ(1+c)]=0.

(19)

式(19)中三项分别对应弹性约束圆弧拱的屈曲模式和导致结构失稳的临界径向约束刚度.

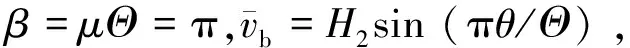
(20)

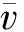
(21)

当λ<λsb1时不发生不对称分岔屈曲；当λ>λsb1，β=π时不对称分岔屈曲对应的位移大于跳跃屈曲对应的位移，结构先发生跳跃屈曲再发生不对称分岔屈曲，二者可通过另一个临界深浅参数λsb2界定，它可令β=π时式(11), 式(15)的解相同得到.

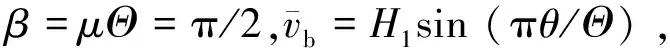
(22)

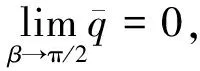
λsn=π3(1+αw+Θ+αw-Θ)/8.

(23)

可知，λ=λsn结构发生对称屈曲，αv±Θ不影响λsn值；λ<λsn时结构没有屈曲；λ>λsn时拱发生跳跃屈曲，临界荷载可通过式(11), 式(15)求得.

3)当1-β2αv+Θ(1+c)=0时，基本解为：

屈曲时轴力为：

(24)

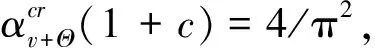
(25)

当λ<λss时，结构没有屈曲，当λ>λss时，发生跳跃屈曲.式(25)的一种极端情况是c=1，即两端径向刚度相等，可知此时结构没有屈曲.

1.5 屈曲特性与λ的关系

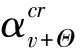
表1 拱的屈曲特性与边界刚度及深浅参数的关系表

2 数值分析

本节对上一节理论解进行数值讨论，并与有限元结果进行对比验证，研究深浅参数λ及约束刚度对屈曲模式、屈曲路径及临界荷载的影响.

2.1 与有限元的对比验证

图2给出了本文方法和有限元法的对比结果，弹性约束圆弧拱中αv±Θ,αw±Θ已知，有限元分析时E=200GPa,A=5.5×103mm2,I=6.6×107mm4，图2纵、横坐标分别为无量纲化的外荷载、跨中位移，f为矢高，左、右临界屈曲荷载点分别对应加、卸载.由图2可知两种方法求解的弹性约束拱屈曲路径吻合很好，屈曲荷载相差很小，说明本文方法可行.由图2还可知，在外荷载增大时，分岔屈曲临界荷载小于跳跃屈曲临界荷载，结构发生分岔屈曲，这与上一节理论分析结果一致.

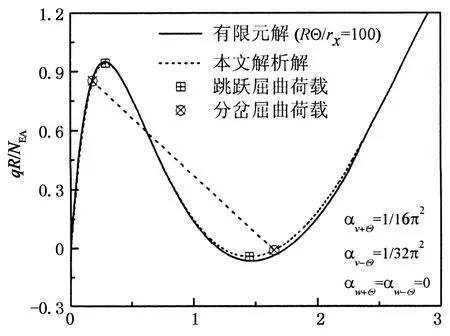
vc/f

图3针对不同深浅参数λ时的屈曲荷载进行了讨论，在λ的区间上有λsb1和λsb2两个临界参数，本文方法和有限元法的对比显示，当λ<λsb2时，有限元结果与跳跃屈曲的临界荷载吻合很好，而当λ>λsb2时有限元结果除了在λ值较大的位置外均与分岔屈曲的结果吻合很好，这说明λsb2在一定程度上是区别深拱和浅拱的参数，也更进一步证明了前述理论结果.

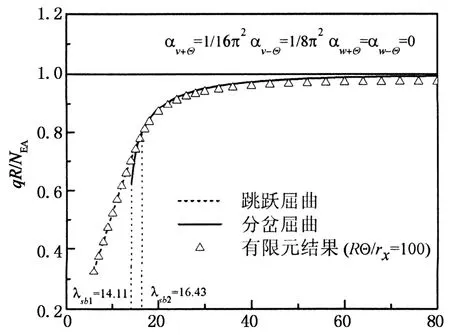
λ

2.2 λ对屈曲特性的影响

图4和图5分别给出了临界深浅参数与径向、轴向约束刚度的对应关系.图4显示λsb1和λsb2均随着αv+Θ和αv-Θ的增加而增加，且变化曲线均从同一位置出发，此时αv±Θ=0.图5中对于任意的αw+Θ+αw-Θ，从小至大依次为λsn，λsb1和λsb2，当λ位于3条曲线所分成的4个区域时，结构呈现不同的屈曲模式和屈曲荷载，与表1对应.

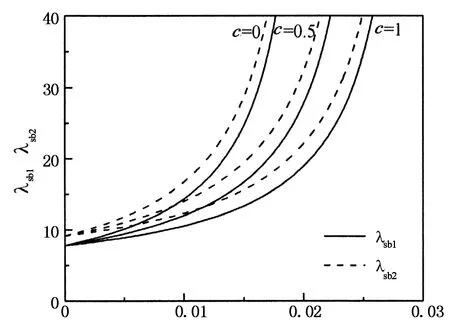
αv+Θ

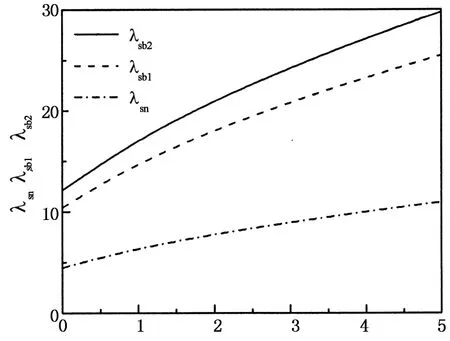
αw+Θ+αw-Θ

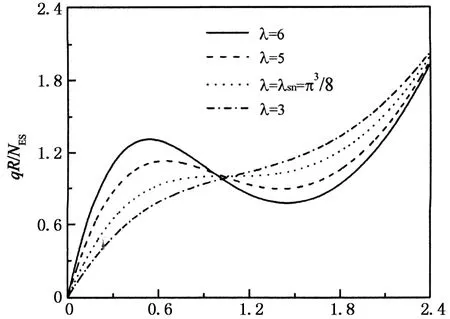
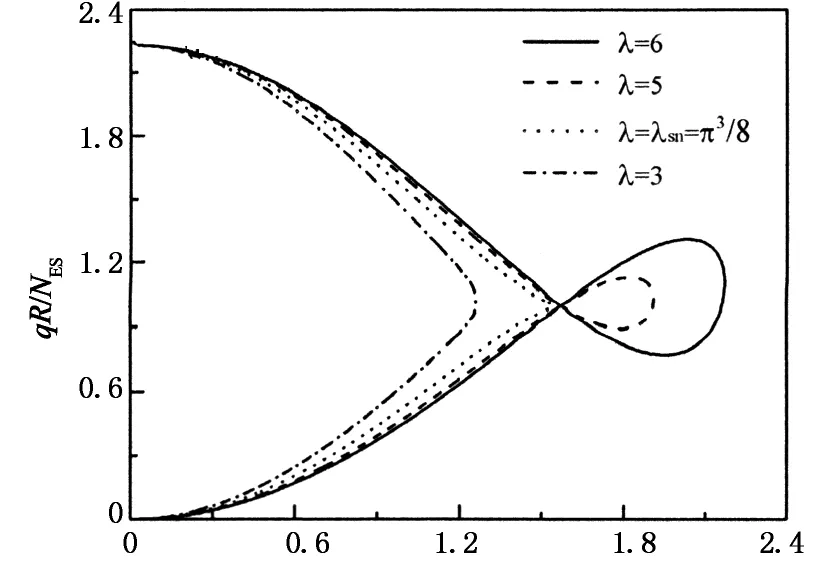
图6给出了不同λ的屈曲路径及内力分布图，图6(a),(b)纵坐标均为无量纲化的外荷载，横坐标分别为无量纲化的跨中径向位移和轴力参数β.由图6可知，当λ=λsn时，结构发生对称分岔屈曲，荷载位移曲线未呈现跳跃特性，发生屈曲时对应轴力为β=π/2(图6(b)中点线)；当λ=3<λsn时，结构不发生屈曲(如图6(a)所示)，这与前述理论结果一致，另外对应轴力β<π/2(图6(b))；当λ=5或6(>λsn)时，荷载位移曲线出现跳跃特性，外荷载增至一定程度时发生跳跃屈曲，另外轴力参数出现β>π/2的情况，位移曲线和内力曲线的极值点对应临界荷载.

2.3 约束刚度对屈曲特性的影响

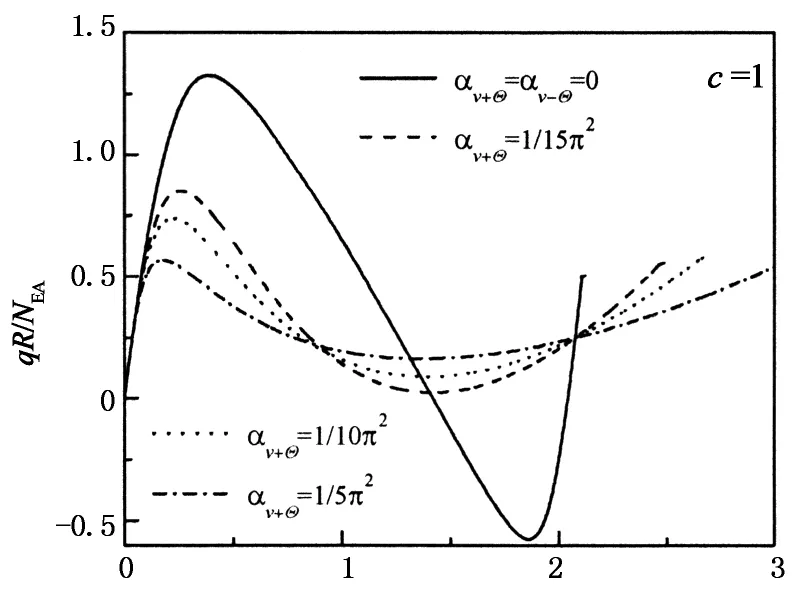
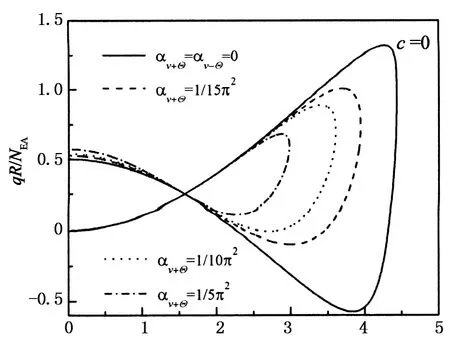
图7给出了αv±Θ(径向弹性约束)的影响，且两端刚度值相等(c=1)，为便于比较αv±Θ=0(两端铰支，可视为弹性约束的极端情况)时的屈曲特性也一并放入.如图7(a)所示，随着αv+Θ的增大结构临界屈曲荷载变小，即结构越柔其承载能力越低；另外αv+Θ不同时结构内力也不相同(如图7(b)所示)，αv+Θ越大内力越小，αv±Θ=0(两端铰支)的屈曲内力最大.

vc/f

β

vc/f

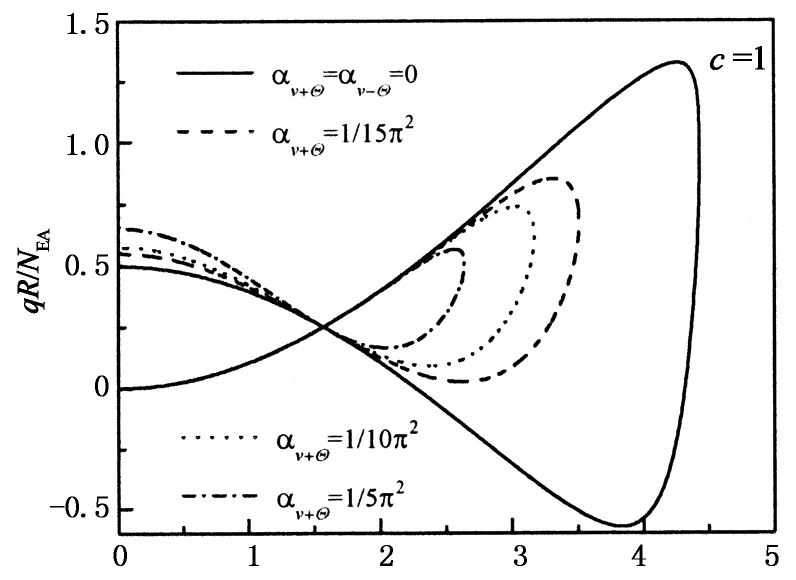
β

图8给出了当c=0时αv±Θ的影响，此时拱结构一端弹性约束另一端固结，为便于比较，αv±Θ=0时的屈曲特征也一并放入.如图8(a)所示，αv+Θ增加即约束刚度减小时屈曲临界荷载减小，αv+Θ=0时临界荷载最大，即径向弹性约束的存在降低结构承载能力，且αv+Θ越大降低越多.另外，图8(b)也给出了αv+Θ变化过程中的轴力分布，αv+Θ越大屈曲临界荷载对应轴力越小，而αv+Θ=0时屈曲对应的轴力最大.

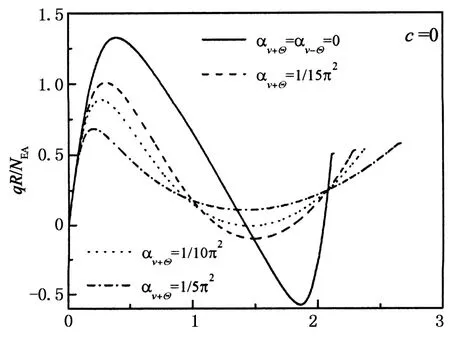
vc/f

β

图9给出了不同αv±Θ时临界屈曲荷载与深浅参数λ和展开角2Θ的关系.从图9(a)可知，λsb2是确定临界屈曲荷载的一个重要参数，当λ<λsb2时，发生跳跃屈曲，临界荷载由式(10),(11)求解；当λ>λsb2时，发生分岔屈曲，临界荷载由式(10)令β=π求得，且λ较大时不同αv±Θ对应的临界屈曲荷载相差较小；αv±Θ对λsb2的大小影响显著，总的说来刚度越大λsb2越小.在图9(b)临界屈曲荷载与展开角2Θ的关系图中，λsb2将展开角2Θ分为跳跃屈曲和分岔屈曲两个区间，αv±Θ同样对λsb2的大小影响显著，实际上这与其定义λ=RΘ2/rx是一致的.此外，在图9中均可发现临界屈曲荷载随约束刚度的增大(或柔度参数αv±Θ的减小)而增大.

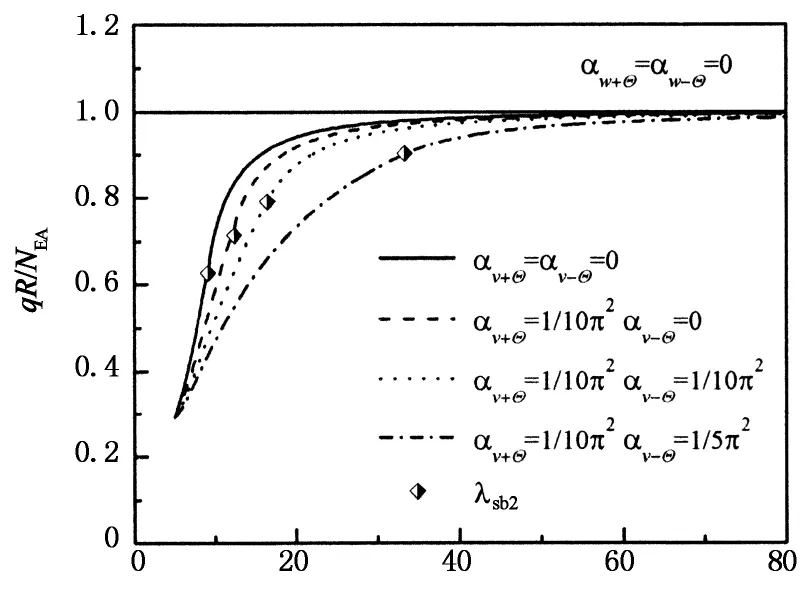
λ

2Θ

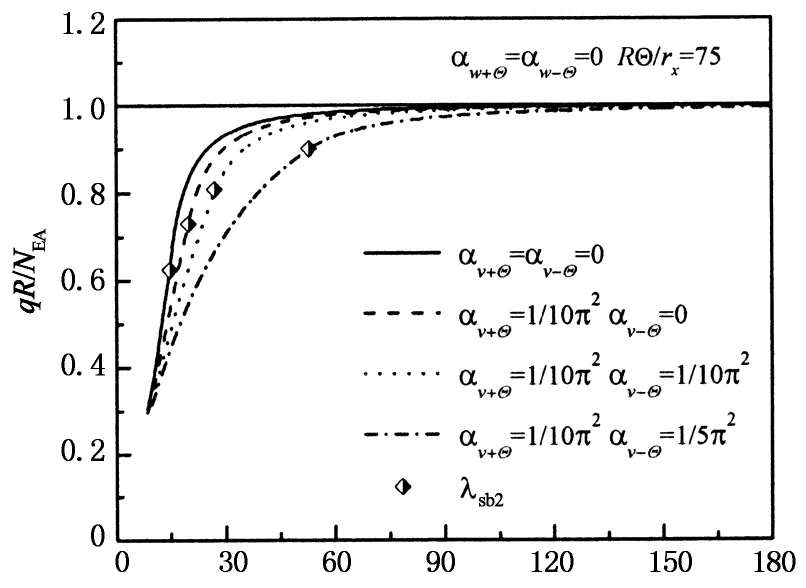
图10给出了不同αw±Θ时临界屈曲荷载与λ和2Θ的关系图.由图10可知，λsb2是界定屈曲模式及临界屈曲荷载的重要参数，当λ<λsb2时，跳跃屈曲对应的临界荷载由式(10), (11)求解；当λ>λsb2时，分岔屈曲对应的临界荷载在式(10)中令β=π求得，且λ和2Θ较大时不同αw±Θ对应的屈曲荷载差异较小.与αv±Θ的影响不同，各种αw±Θ对应的λsb2差异较小；与αw±Θ的影响相同的是屈曲荷载均随约束刚度的增大(或柔度参数αw±Θ的减小)而增大.

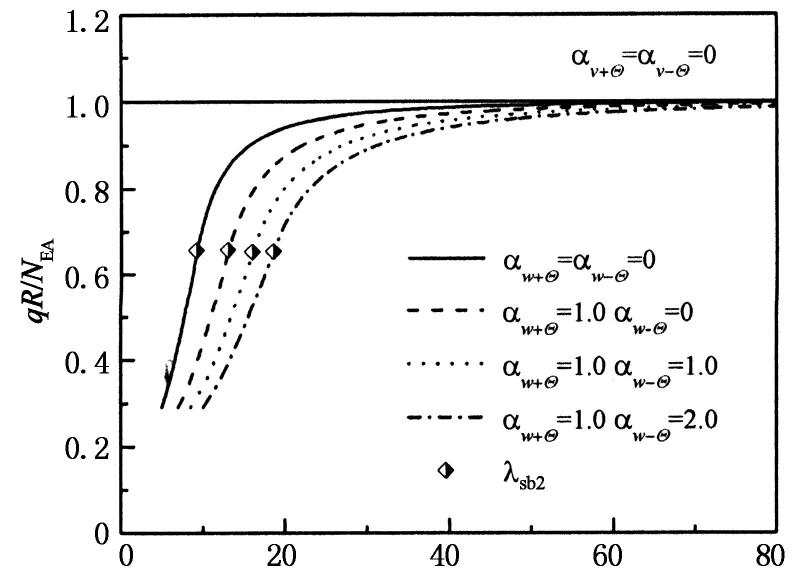
λ

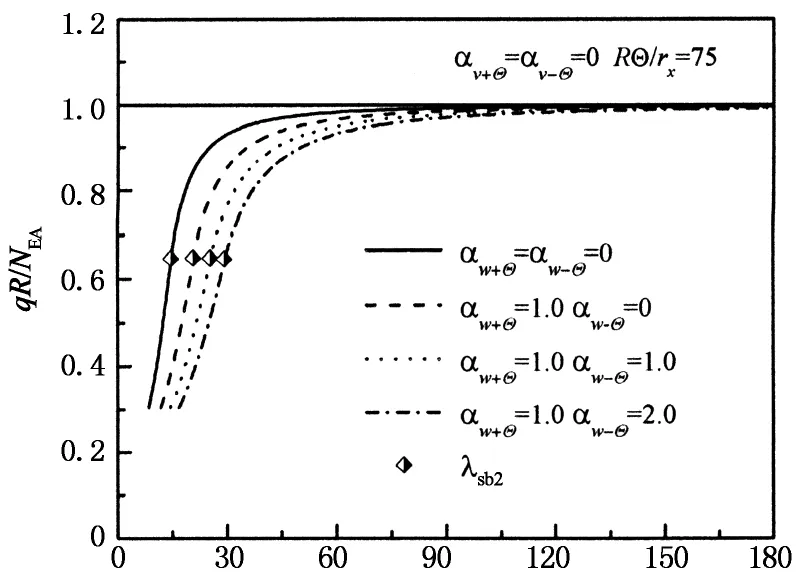
2Θ

3 结 论

本文将圆弧拱的非理想边界考虑为沿径向和轴向的弹性约束，利用能量变分原理建立了结构的非线性方程，得到了外荷载与结构内力、径向位移的关系，分析了各种约束条件下的屈曲路径和临界荷载，并与有限元结果进行了验证，主要结论如下：

1) 所得屈曲路径与临界荷载与有限元结果吻合良好，证明本文方法可行.

2) 临界竖向约束参数和深浅参数λsn,λsb1和λsb2对结构的失稳模式起决定性的作用，它们将圆弧拱按基本参数划分为不同的失稳区间.

3) 各种径向、轴向约束刚度下，λ<λsb2时结构发生跳跃屈曲，λ>λsb2时发生分岔屈曲，且径向、轴向约束刚度增大时屈曲临界荷载均增大.

[1] 项海帆, 刘光栋. 拱结构的稳定与振动[M]. 北京: 人民交通出版社, 1991：1-332.

XIANGHai-fang,LIUGuang-dong.Stabilityandvibrationofarch[M].Beijing:ChinaCommunicationsPress, 1991:1-332.(InChinese)

[2] 赵跃宇, 易壮鹏, 王连华. 初始应力对钢管混凝土拱桥面内极限承载能力的影响[J]. 湖南大学学报:自然科学版, 2007, 34(3): 1-5.

ZHAOYue-yu,YIZhuang-peng,WANGLian-hua.Effectsofinitialstressonthein-planeultimatebearingcapacityofCFSTarchbridges[J].JournalofHunanUniversity:NaturalSciences, 2007, 34(3): 1-5. (InChinese)

[3]KIMNI,KIMMY.Exactdynamicstiffnessmatrixofnon-symmetricthin-walledcurvedbeamssubjectedtoinitialaxialforce[J].JournalofSoundandVibration, 2005, 284(3/5): 851-878.

[4]MALHOTRAN,NAMACHCHIVAYANS.Chaoticmotionofshallowarchstructuresunder1∶1internalresonance[J].JournalEngineeringMechanics, 1997, 123(6): 620-627.

[5]MALHOTRAN,NAMACHCHIVAYANS.Chaoticdynamicofshallowarchstructuresunder1∶2resonance[J].JournalEngineeringMechanics, 1997, 123(6): 612-619.

[6] 易壮鹏,康厚军,王连华.弹性支撑浅拱的非线性动力行为分析[J].动力学与控制学报,2013,11(2):142-148．

YIZhuang-peng,KANGHou-jun,WANGLian-hua.Researchonthenonlineardynamicbehaviorsofelasticsupportshallowarch[J].JournalofDynamicsandControl,2013,11(2):142-148. (InChinese)

[7] 韩强，黄怀纬，樊学军．弹性浅拱的非线性动力屈曲[J]．华南理工大学学报:自然科学版, 2010, 38(3): 1-7.

HANQiang,HUANGHuai-wei,FANXue-jun.Nonlineardynamicbucklingofshallowelasticarch[J].JournalofSouthChinaUniversityofTechnology:NaturalScienceEdition, 2010, 38 (3): 1-7. (InChinese)

[8]PIYL,BRADFORDMA,UYB.In-planestabilityofarches[J].InternationalJournalofSolidsandStructures, 2002, 39(1): 105-125.

[9]PIYL,BRADFORDMA,LOIFT.Nonlinearanalysisandbucklingofelasticallysupportedcircularshallowarches[J].InternationalJournalofSolidsandStructures, 2007, 44(7/8): 2401-2425.

[10]PIYL,BRADFORDMA.Nonlinearin-planeelasticbucklingofshallowcirculararchesunderuniformradialandthermalloading[J].InternationalJournalofMechanicalSciences, 2010, 52(1):75-88.

[11]卫星，李俊，李小珍，等．考虑二阶效应的拱结构面内弹性屈曲[J]．工程力学, 2007, 24(1): 147-152．

WEIXing,LIJun,LIXiao-zhen,etal. In-plane secondary buckling behavior of elastic arches [J]. Engineering Mechanics, 2007, 24(1): 147-152.(In Chinese)

[12]程鹏，童根树．圆弧拱平面内弯曲失稳一般理论[J]．工程力学，2005, 22(1): 93-101.

CHENG Peng, TONG Gen-shu. A general theory for in-plane nonlinear analysis of circular arches [J]. Engineering Mechanics, 2005, 22(1): 93-101. (In Chinese)

[13]郭彦林，林冰，郭宇飞．压弯圆弧拱平面内稳定承载力设计方法的理论与试验研究[J]．土木工程学报, 2011, 44(3):8-15.

GUO Yan-lin, LIN Bing, GUO Yu-fei. Theoretical and experimental studies of in-plane stability design of circular arches subjected to axial force and moment [J]. China Civil Engineering Journal, 2011, 44(3): 8-15. (In Chinese)

[14]鹫津久一郎．弹性和塑性力学中的变分法[M]．老亮，郝松林，译．北京：科学出版社，1984:1-446.

WASHIZU Kyuichiro. Variational methods in elasticity and plasticity [M]. Translated by LAO Liang, HAO Song-lin. Beijing:Science Press, 1984:1-446. (In Chinese)

[15]易壮鹏．几何缺陷对拱结构力学性能的影响[D]．长沙：湖南大学土木工程学院, 2007:29-66.

YI Zhuang-peng. The effects of the geometrical imperfections on the mechanical properties of arch structures [D]. Changsha: College of Civil Engineering, Hunan University, 2007:29-66. (In Chinese)

Planar Buckling Mode and Critical Load for Arch Structure with Non-ideal Boundary

KANG Hou-jun1， YI Zhuang-peng2†， ZENG You-yi2

(1. College of Civil Engineering, Hunan Univ，Changsha,Hunan 410082, China;2.School of Civil Engineering and Architecture, Changsha Univ of Science and Technology,Changsha,Hunan 410114, China)

The non-ideal boundary conditions (neither fixed nor hinged) of arch structure were considered as an elastic constraint with certain stiffness in different directions, and the nonlinear equilibrium equation was determined by using deformation geometric relation and energy variation principle. A circular arch under radial uniform load was taken as an example to establish the relationships between the external load and the internal force, and the radial displacement. By defining the shallowness and critical constraint stiffness, the snap-through buckling and bifurcation buckling were studied and the occurrence condition and distribution range were investigated. The buckling path and critical buckling load in the proposed method were in good agreement with the results from the finite element method. And the numerical method was used to study the buckling path and critical buckling load for different stiffness of elastic constraint. The results show that the critical shallowness and the critical constraint stiffness play a fundamental role in the buckling mode and critical buckling load for circular arch.

buckling; circular arch; non-ideal boundary;bifurcation buckling; variation principle

1674-2974(2015)05-0058-07

2014-09-09

国家自然科学基金资助项目(11002030, 11102063),NationalNaturalScienceFoundationofChina(11002030, 11102063)

康厚军(1977-)，男，四川安岳人，湖南大学副教授，博士

†通讯联系人，E-mail:yizhuangpeng@163.com

O343.9

A