飞行器姿态运动系统的控制——噪声方法

刘 红，苗秀凤

(1. 哈尔滨金融学院 基础部，哈尔滨 150030；2. 哈尔滨工业大学 理学院 数学系，哈尔滨 150001)

飞行器姿态运动系统的控制
——噪声方法

刘 红，苗秀凤

(1. 哈尔滨金融学院 基础部，哈尔滨 150030；2. 哈尔滨工业大学 理学院 数学系，哈尔滨 150001)

研究了空间飞行器姿态主动控制系统的混沌控制， 在非线性系统中加入Gauss白噪声以实现对该混沌系统的控制，对系统的混沌行为加以抑制，使系统稳定化.采用最大Lyapunov指数法，通过Matlab数值仿真技术，对原系统以及随机相位控制后的系统Lyapunov指数随时间的变化趋势进行观察，可以看到原系统为混沌状态，而随机相位控制后的系统混沌已被控制住.在计算最大Lyapunov指数的过程中采用了线性随机系统的Khasminskii球面坐标变换方法.此外，针对所研究的系统给出了相图，时间历程图和Pioncar e′截面图来验证所得到的结论，证实所用方法是有效的.

混沌控制；Gauss白噪声；随机相位；Lyapunov指数；Pioncar截面

H·Poincar e′对混沌的特征表述为“某些确定系统具有内在随机性”，他提出了很多非常重要的理论及概念，对后来动力系统的理论发展都有着很深远的影响，比如奇异点、同宿和异宿等，以及稳定性理论、分岔理论、奇异性理论和吸引子理论等非常具有创造性的理论.美国气象学家E·N·Lorenz曾发表过一篇论文“决定性非周期流”，讨论了天气预报的时候遭遇的一些问题，并在这些问题的解决过程中给出了一个常微分方程组，所考虑的状态空间是三维的，即著名的Lorenz方程[1]

(1)

它研究的是无限平板间的流体热对流运动，这个方程是其简化模型，容易看出该方程是一个自治方程.变量x1,x2,x3是一组变量，其中x1的物理含义是正比于对流强度的一个变量；x2的物理含义是正比于上升流和下降流的温差的一个变量；x3的物理含义是正比于温度分布垂直方向非线性强度的一个变量.在这个方程组中有三个待定的参数，分别为a,b和c，它们的物理意义分别表示：a被称为Prandt数；b表示的是与对流纵横比有关的外形比，叫做Rayleigh数，表示引起湍流和对流的驱动因素，方程 (1) 的主要控制参数为a=10，b=8/3，c=28时，方程 (1) 的解呈现出很混乱的情形，是一个非周期的解.Lorenz方程是混沌现象被发现的第一个重要例证.

混沌控制指的是人为的对混沌系统施加影响，使得系统向预想的状态发展.即下面的这几种情况：1) 在混沌运动对我们不利时，对其给予抑制；2) 在混沌对我们有利时，采取办法生成混沌状态并进行有效的利用；3)如果系统已经是混沌状态，采取适当的控制手段，得到我们需要的输出.举例说明，众所周知混沌轨道是一个非周期的，它在变量空间中混沌吸引子的维数比其他任何的周期吸引子都要大，那么就可以选择在整个混沌吸引子的范围内来对其进行控制.另外，我们知道混沌运动具有初值的敏感性，这样一来较为邻近的轨道之间的距离随着时间的变化会迅速以指数形式发散，进而导致混沌运动长期行为的不可预见性.

Li-Yorke定理：设f(x)是[a,b]上的连续自映射，若f(x)有3周期点，则对任意正整数n，f(x)有n周期点[2].

设连续自映射 f:T→T⊂R,T是集合R中的一个子区间.

假设存在一个不可数的集合D⊂T

使得

1) D中无周期点

2) 对∀X1，X2∈D,当X1≠X2时，有：

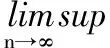
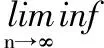
这里fn(·)表示函数f(x)的n重函数关系.

3) 对∀X∈D和f(x)的任一周期点P有：

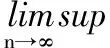
(2)

则我们说f(x)在集合D上表现为混沌.

根据Li-Yorke对混沌理论的阐述，在1983年Day提出一个混沌系统要具有如下三个特点：

1) 在混沌系统中有阶数任意的周期轨；

2)在该系统中存在着一个不可数的集合，在这个集合中只包含混沌轨道，而且在此集合中的任意两个轨道表现为在任意的时间内都不趋向于远离或者靠近，而是这两种状态也即远离和靠近轮换出现，并且任何一个轨道都不能无限趋于周期轨，也就是说在这个集合中存在渐近周期轨；

3)混沌轨道是非常不稳定的[3-6].

目前Lyapunov指数是公认的判断混沌最为可靠的一种定量方法[7-11].下面就对Lyapunov指数的定义给以叙述：设x(t)(x∈Rm)表示m维相空间中的动力系统的运动轨道.用x(t)+δx(t)表示任意相邻的运动轨道，则轨道x(t)的LCE可以表示为：

从上式可以看出Lyapunov指数LCE的物理意义，Lyapunov指数实际上可以看作是由m个数组成的谱.Lyapunov指数可以是正数、负数或者为零.如果Lyapunov指数为正数，即系统在相应方向上表现为发散，如果Lyapunov指数为负的，则表示该系统在相应方向上表现为收缩.针对一个自治系统而言，若所有的Lyapunov指数均为负值，则系统表现为趋于稳定；如果其中有为零的Lyapunov指数，而且除了零Lyapunov指数以外的其他Lyapunov指数为负值，那么系统就表现为做周期运动；我们所说的混沌运动情形实际上是指其存在正的Lyapunov指数并而且同时系统作往复运动.如果正的Lyapunov指数不小于两个的时候，系统表现为超混沌运动.

1 飞行器姿态运动的混沌现象

为了更好的让飞行器可以在已经设定的轨道坐标系保持稳定性，可以采用一些被动稳定方案[12-16]，但最好可以利用控制系统的性质实现对飞行器姿态的主动稳定控制[17].和被动稳定方案相比较，主动姿态稳定有其特有的优点，可以确保更高的精度和速度，但也有不足，复杂化的结构导致可靠性降低，而且能源消耗也随之增加，因此当精度要求较高和力矩扰动较大时比较适用.飞行器主动姿态稳定系统主要包括喷气三轴稳定系统、以飞轮为主的三轴稳定系统和磁力矩器轴稳定系统.其中第一种系统其运行主要是根据质量排出反作用喷气进而产生控制力矩的原理进行.在研究非线性控制系统时较为常用的分析方法是Lyapunov指数法和相平面图解法.相平面法就是利用姿态角和角速度所组成的平面来研究该系统在相平面中的运动轨迹.相平面法对于比较简单的低阶非线性系统的研究来说既简单又直观的.而且通过相平面还可以研究过渡过程时间、超调量、极限环等主要姿态控制性能指标.而对于模型维数较高的飞行器来说，就需要完成更高维的控制目标.为了使得控制任务更趋合理，通常将飞行器的轨道控制任务与姿态控制结合起来，组成一个多推力器的系统.在这样复杂的执行机构系统设计时，就需要保证推力器的数目与分布安装位置要达到可靠性要求，还要尽量少的消耗能源.在这种情形下，需要研究如何通过计算机对系统操作任务进行设计，最优地分配推力器的工作以及节约时间.

(3)

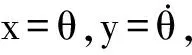
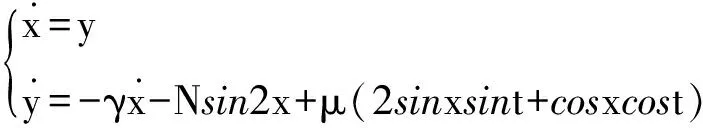
(4)

进而线性化得到

(5)

将最大的Lyapunov指数定义为：

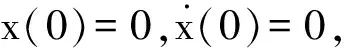
图1 Lyapunov指数图

令

θ：R1→S1

t→θ(t)=ωt,mod2π

方程(4)可以转化为

(6)

再定义截面如下：

∑θ0={(x,θ)∈Rn×S1|θ=θ0∈(0,2π]}

(7)

可以做出庞加莱截面，如图2(A)所示.

再做出方程 (3) 的相图和时间历程图，如图2(B) 和 (C)所示.

由图2(A)可见庞加莱截面为混沌吸引子.由图2(B) 和 (C)可以很容易发现下面的事实：相轨表现比较混乱且时间历程图无周期性可言，上述事实说明了原系统是混沌的，没有确定的规律可以依循.

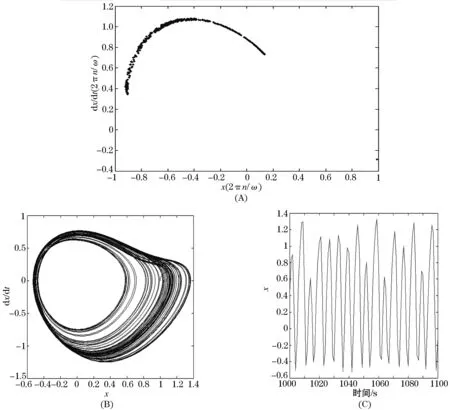
图2 (A)庞加莱截面；(B)系统的相图；(C)时间历程图

2 利用随机相位对飞行器姿态运动的混沌控制

下面对原系统进行随机相位控制，在飞行器姿态运动方程(2) 的相位中加入高斯白噪声(强度为σ)，有：

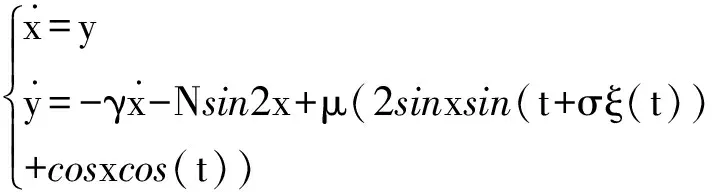
(8)

这里ξ(t)为标准Gaussian白噪声，σ为其强度，ξ(t)满足：Eξ(t)=0，Eξ(t)ξ(t+τ)=ζ(τ)，这里ζ(τ)为Dirac-delta函数.

同理可以得到式(8)的线性化形式

(9)

令

其中

f=-2Ncos2x+2μcosxsin(t+σξ(t))-μsinxcos(t)

这样式(9)变为

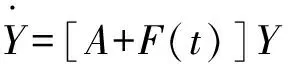
(10)

定义最大Lyaponov指数为

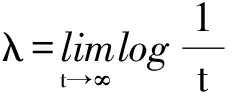
(11)

这里

Wedig引入了一种计算最大Lyapunov指数的方法即Khasminslii球面坐标变换方法[18-19]，利用这个计算方法可令

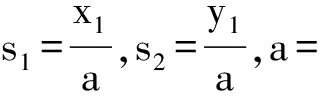
(12)

则

(13)

其中

(14)

针对方程 (8) 与 (9) 用四阶Runge-Kutta方法进行求解再并结合式(10)～(14)，可以求得Lyapunov指数的值.考虑到在求解过程中会有随机因素带来的影响，选择多次模拟这个求解过程，然后取平均最大Lyapunov指数，以期尽量接近真值，下面画出平均最大Lyapunov指数随噪声强度变化的曲线，如图3所示.

从图3中可知，在σ小于临界值σc=0.05的时候，平均最大Lyapunov指数λ的符号为正，当σ>0.05时，λ的符号由正转负，这就说明系统已经由混沌状态过渡到稳定状态.

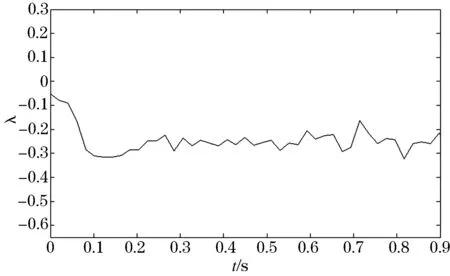
图3 最大Lyapunov指数随噪声强度变化图

取噪声强度σ=0.1，下面对这个系统加以控制并做出控制后该系统的庞加莱截面、相图、时间遍历图，如图4(A)、(B)和(C)所示.

图4 (A)庞加莱截面；(B)系统的相图；(C)时间遍历图

从图2(A)、(B)、(C)和图4(A)、(B)、(C)的比较中可以发现如下现象：庞加莱截面中的混沌吸引子已经变为稳定吸引子，相图轨道也变成了稳定的环形轨道，时间历程由不规则变为规则的周期形态.也就是说原来的混沌状态得到了控制.

3 结 语

本文研究了利用在飞行器姿态运动的混沌系统中加入白噪声的方法以对其混沌行为进行控制，首先对飞行器姿态运动系统作了状态描述，在对这个系统的控制过程中我们给出了最大Lyapunov指数随噪声变化的曲线示意图、Poincaré 截面等，阐释了在给定的参数条件下所研究的系统表现为混沌状态.然后想办法对这种混沌行为加以控制，经过研究所加入的噪声强度与最大Lyapunov指数之间的关系发现，当强度大于0.1时平均最大Lyapunov指数转为负值.另外给出了相图和时间历程图也充分证实了这些结果.

[1] LORENZ E N. Deterministic non-periodic flow[J]. J. Atmos. Sci., 1963, 20: 130-141.

[2] LI T Y, YORKE J A. Period Three Implies Chaos[J]. American. Math. Monthly, 1975, 82(1): 985-992.

[3] LIPOWSKI A, LIPOWSKA D. Nonequilibrium phase transition in a lattice prey-predator system[J]. Physica A ,2000, 276: 56-64.

[4] MUKHERJEE D. Uniform persistence in a generalized prey-predator system with parasitic infection[J]. Bio System, 1998, 47: 149-155.

[5] OGATA K. Modern control engineering[M]. Englewood Cliffs, NJ: Prentice-Hall, Inc, 1970.

[6] PITCHFOREED J, BRINDLEY J. Neurotrophic predation in simple prey-predator models[J]. Bull Math Biol, 1998, 60: 937-953.

[7] GRADSHTEYN I S, RYZHIK I M. Table of integrals, series and products[M]. San Diego: Academic Press, 1980.

[8] GRAY G L, KAMMER D C, DOBSON I. Heteroclinic bifurcations in rigid bodies containing internally moving parts and a viscous damper[J]. J Appl Mech Trans ASME, 1999, 66: 720-728.

[9] GUCKENHEIMER J, HOLEMS P. Nonlinear oscillations, dynamical systems and bifurcations of vector fields[J]. New York: Springer-Verlag, 1983.

[10] HALE F J. Introduction to space flight[M]. Englewood Cliffs: Prentice-Hal, 1994.

[11] ZHOU C, HE T. Chaotic annealing for optimization[J]. Physical Review E, 1997, 53 (3): 2580-2587.

[12] 余后满, 郝文宇, 袁俊刚, 等. 航天器系统工程技术发展思路[J].飞行器工程, 2009, 18 (01) : 1-7.

[13] 王礼恒. 中国航天系统工程[J]. 航天工业管理, 2006(10): 60-64.

[14] HASKINS C. INCOSE system engineering handbook-aguide for systemlife cycle processes and actives[M]. 3rd ed. INCOSE, 2006.

[15] 朱鲁青, 张鑫伟. 国外中小型航天器技术发展研究[J]. 国际太空, 2010, (09): 1-9.

[16] 于洪洁, 刘延柱. 复杂力场中磁性刚体航天器混沌姿态运动的控制[J]. 上海交通大学学报, 2004, 38(8): 1408-1411.

[17] LI G H, ZHOU S P. Anti-synchronization in diferent chaotic systems [J]. Chaotic Solitons and Fractals, 2007, 32(2): 516-520.

[18] WEDIG W V. Dynamic Stability of Beams under Axial Forces: Lyapunov Exponents for General Fluctuating Loads, in Proceeding Eurodyn'90[C]//Conference on Structural Dynamics, 1990. 57-64.

[19] 王 纯.高超声速飞行器上升段轨迹设计[J].哈尔滨商业大学学报：自然科学版，2014，30(6)：728-731.

Spacecraft attitude system control—noise method

LIU Hong, MIAO Xiu-feng

(1.Department of Foundation,Harbin Finance University, Harbin 150001, China;2. Department of Mathematics, Harbin Institute of Technology, Harbin 150001, China)

This paper studied the chaos control of the spacecraft attitude active control system. The method used in this paper was to add the Gaussian white noise to the system in order to control this chaotic system. Suppressed the chaotic behavior to make stabilization. The largest Lyapunov exponent was adopted, and got the data through the numerical simulation technology of Matlab. Through the trending of the Lyapunov exponent changing with the time of the original system and the random phase control system, found that the original behavior was chaotic, and the controlled system was stable. The method for computing the top Lyapunov exponent was based on the Khasminskii’s formulation for linear stochastic systems. In addition, phase portraits, time evolution and Poincar e′map were plotted to confirm the obtained results which confirm the method was effective.

chaos control; Gauss white noise; random phase; top Lyapunov exponents; Poincar e′map

2014-06-10.

刘 红(1979-)，女，硕士，讲师，研究方向：应用数学.

V249

A

1672-0946(2015)01-0090-06