时滞离散马尔科夫跳跃系统l2-L∞的滤波

王红茹，由珊珊

(哈尔滨工程大学 信息与通信工程学院，哈尔滨 150001)

时滞离散马尔科夫跳跃系统l2-L∞的滤波

王红茹，由珊珊

(哈尔滨工程大学 信息与通信工程学院，哈尔滨 150001)

针对时滞离散马尔科夫跳跃系统的l2-L∞滤波问题进行的研究，通过建立的l2-L∞性能准则，采用线性矩阵不等式(LMI)技术推导出l2-L∞滤波器存在的充分条件，在推导过程中引入附加矩阵，降低了滤波器的保守性.所设计的滤波器不但保证了滤波误差系统随机稳定，而且满足给定的l2-L∞性能指标.仿真算例表明所设计的滤波器是可行的.

l2-L∞滤波；时滞系统；线性矩阵不等式

作为系统和控制的重要问题之一，滤波被广泛应用在状态估计中，以测量信号为基础对系统内部的不可测量的信号进行估计.众所周知，经典的卡尔曼滤波是处理状态估计问题的有效方法，但是卡尔曼滤波需要确定已知的系统模型和外部噪声信号，当不满足以上两点时，经典卡尔曼滤波就不再适用，这一特点使得研究鲁棒滤波问题势在必行.

另一方面，时滞常常存在于实际的动态系统中，例如网络控制系统，通信系统等，同时也是造成系统的不稳定性和低性能指标的来源，带有时滞马尔科夫跳跃系统可以更加准确的描述实际系统的动态模型，因此研究时滞马尔科夫跳跃系统的l2-L∞滤波受到很多学者的关注，文献[1]通过Lyapunov-Krosovski函数，推导l2-L∞滤波器的存在条件，所针对的系统是时变延迟带有部分未知转移概率的连续马尔科夫跳跃系统.文献[2]对于离散马尔科夫跳跃系统，采用时滞分割技术，建立时滞依赖条件，保证滤波误差系统随机稳定，所设计的滤波器降低了保守性.文献[3]对于时滞连续马尔科夫跳跃系统设计了指数l2-L∞全阶滤波器，保证了滤波误差系统的均方稳定.

本文研究时滞离散马尔科夫跳跃系统的l2-L∞滤波问题，引入了附加矩阵，使得Lyapunov矩阵与系统矩阵的乘积项解耦，降低了保守性，并推导出l2-L∞性能准则，应用LMI技术得到了滤波器存在的充分条件.所设计的滤波器不但保证了滤波误差系统随机稳定，而且满足给定的l2-L∞性能指标.数值仿真表明所设计的方法是可行的.

1 问题描述

考虑下面时滞马尔科夫跳跃系统：

(1)

(2)

其中:AFi，BFi，CFi为所设计的滤波器的参数矩阵.

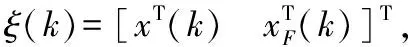
(3)

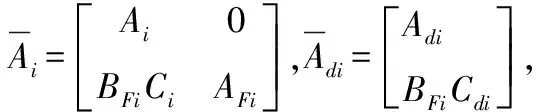
则噪声信号ω(k)到估计误差e(k)的z传递函数为

(4)

定义1：滤波误差系统(3)在ω(k)=0时，若在任意初始状态下，满足

则称系统(3)随机稳定.

本文所要研究的问题是在给定系统(1)，设计滤波器(2)，使得滤波误差系统(3)在零初始条件下随机稳定且满足

‖e‖ε∞<γ‖ω‖2

(5)

即满足l2-L∞扰动衰减水平.

2 l2-L∞滤波器设计

在给出滤波器的设计方法之前，首先考虑一下滤波误差系统(3)的l2-L∞性能准则，给出下列结论.

2.1 l2-L∞性能准则

引理1：考虑系统(1)和滤波器(2)，那么滤波误差系统(3)随机稳定的充分条件为存在矩阵Pi∈R2n×2n>0，Q∈Rn×n>0，满足如下线性矩阵不等式：

(6)

下面给出一个与引理1等价且满足滤波误差系统(3)具有一定的l2-L∞扰动衰减水平的l2-L∞性能判据.

(7)

(8)

其中：K=[I0]

证明：应用Schur补引理[4]式(6)等价于式(9)

(9)

为了建立l2-L∞性能准则，首先选取Lyapunov-Krosovski函数如下：

(10)

下面建立l2-L∞性能准则，设l2-L∞性能指标为，假设在零初始条件下，即当V[ξ(0)θ0]=0，性能指标表示为：

根据选取的Lyapunov-Krosovski函数，可以得到E[ΔV(k)]的表达式如下：

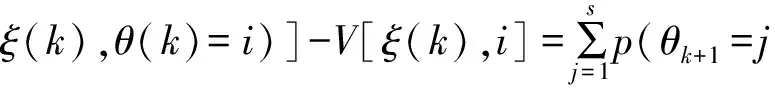
ξT(k)KTQKξ(k)-ξT(k-d)KTQKξ(k-d)

将代入并展开之后，可以进一步得到：

因此可以继续计算l2-L∞性能指标J如下：

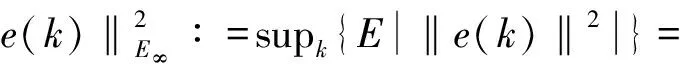
而eT(k)e(k)-γ2ξT(k)Piξ(k)

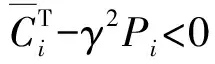
则eT(k)e(k)<γ2ξT(k)Piξ(k)

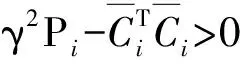
2.2 l2-L∞滤波器设计

基于引理1，给出使得滤波误差系统(3)随机稳定，且保证满足给定的l2-L∞性能指标的滤波器(2)存在的充分条件.

(11)

(12)

滤波器参数矩阵为

(13)

证明：应用Schur补引理式(7)等价于式(14)

(14)

(15)

其中Vi∈Rn×n是任意可逆矩阵，为方便起见，可以定义Vi=I.做如下变量替换：

Si=ZiUiVi

则可获得式(12)和式(11).

3 数值算例

考虑具有两个模态的时滞离散马尔科夫跳跃系统，参数矩阵如下：

模态1：

L1=[1 0.9 0.2 0.5]

模态2：

L2=[0.2 0.4 0.6 0.3]

仿真时，常数时滞d=2，ω(k)为幅值不大于0.5的随机变量，假设系统初始模态θ0=1，按如下模态转换概率：

p11=0.3 ，p12=0.7，p21=0.6，p22=0.4.

θk随机的在两个模态之间变换.

应用Matlab中的LMI工具箱，求解不等式(11)和(12)，得到最优扰动衰减水平和滤波器参数矩阵如下：γ=3.4907

CF2=[-0.9644 -0.1621 -0.3100

-0.1692]

图1可以看出，马尔科夫跳跃系统的模态转换，在模态1和模态2下，计算出两组滤波器的参数矩阵AF1，BF1，CF1和AF2，BF2，CF2.由图2看出，滤波器的状态估计误差趋近于0，证明本文方法得到的l2-L∞滤波器是可行的.

图1 马尔科夫跳跃系统的模态

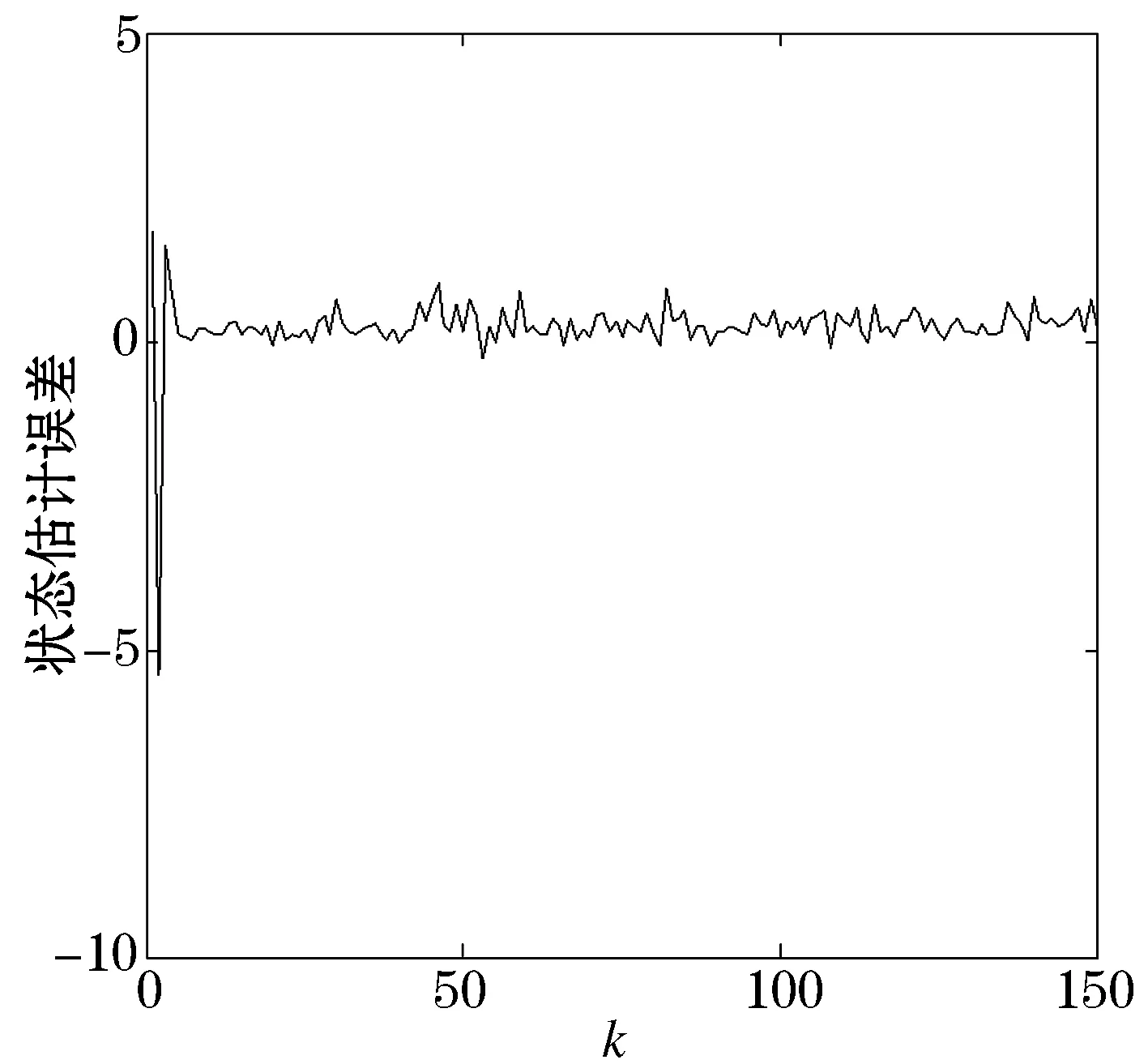
图2 状态估计误差

4 结 语

本文研究的是时滞离散马尔科夫跳跃系统的l2-L∞滤波问题，利用建立的l2-L∞性能准则，给出相应的滤波器设计方法，所设计的滤波器不但保证滤波误差系统随机稳定，而且满足给定的l2-L∞性能指标.在滤波器的设计中，引入附加矩阵，降低了保守性.仿真结果表明了本文方法的可行性.

[1] DING Y C, ZHU H, ZHONG S M,etal. Filtering for Markovian jump systems with time-varying delays and partly unknown transition probabilities [J]. Communication Nonlinear Science Numerical Simulatation, 2012, 17: 3070-3081.

[2] WU Z G, SHI PENG, SU H Y,etal. Filtering design for discrete-time singular Markovian jump systems with time-varying delays [J]. Information Sciences, 2011, 181: 5534-5547.

[3] ZHANG B Y, LI Y M. Exponential filtering for distributed delay systems with Markovian jumping parameters [J]. Signal Processing, 2013, 93(1): 206-216.

[4] 俞 立.鲁棒控制-线性矩阵不等式处理方法[M]. 北京: 清华大学出版社, 2002.

[5] 高会军, 王常虹.不确定离散系统的鲁棒及滤波新方法[J].中国科学(E辑), 2003, 33(8): 695-706.

[6] ZHONG M, YE H, SHI P,etal. Fault detection for Markovian jump systems [J]. IEEE Proc.-Control Theory Appl., 2005, 152(4): 397-402.

[7] 李 伟.改进的基于模糊C-均值聚类的图像分割算法[J].哈尔滨商业大学学报：自然科学版，2013，29(4)：457-461.

Study onl2-L∞filtering for Markov jump systems with time-delays

WANG Hong-ru, YOU Shan-shan

(School of Information and Communication Engineering, Harbin Engineering University, Harbin 150001, China)

The problem ofl2-L∞filter design for discrete-time system with Markov jump was investigated and al2-L∞performance criteria was proposed to guarantee the filtering error systems to be stochastically admissible in this paper. The sufficient conditions for the existence ofl2-L∞filter were presented based on the proposed performance criteria. The problem of filter design was converted into a parameter optimization problem with linear matrix inequality (LMI) constraint. A numerical example was provided to illustrate the effectiveness of the proposed method.

l2-L∞filtering; time-delay systems; LMI

2014-02-26.

王红茹(1969-)，女，副教授，硕士生导师，研究方向：人工免疫网络理论及应用、动态系统的鲁棒故障诊断、动态系统的鲁棒控制、鲁棒滤波及模型降阶等.

TP13

A

1672-0946(2015)01-0050-06