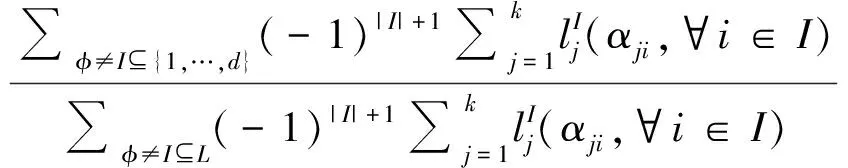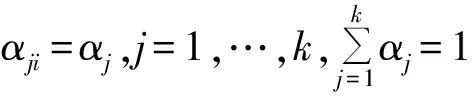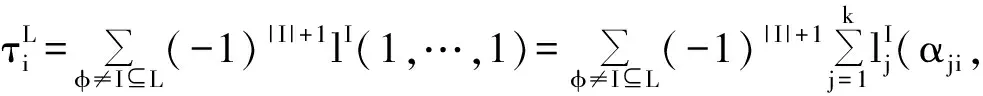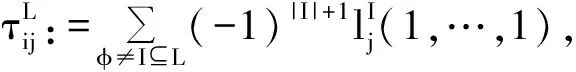一类特殊多元极值Copula的性质

董海燕，梁冯珍

(天津大学 理学院 数学系，天津 300072)

一类特殊多元极值Copula的性质

董海燕，梁冯珍

(天津大学 理学院 数学系，天津 300072)

针对一类构造得到的多元极值Copula，研究它的边界性质及尾部相关度量，并给出尾部相关度量的解析表达式.结果表明，若对参数加以约束，则其上尾相关系数可以表示成构成它的Copula的上尾相关系数的凸和.

极值Copula；尾部相关函数；尾部相关系数

多元极值模型已经被广泛应用于诸多领域，比如金融、保险、环境科学、水文等，在多元极值理论研究中，多元极值Copula在多元极值建模时起着很重要的作用，它具有灵活便捷的建模优越性.Copula的概念首先由Sklar在1959年提出，Sklar定理[1]指出，联合概率分布函数可以分解成Copula和边际概率分布，因此，通过构造多元极值Copula，就很容易得到多元极值分布模型，基于这个思想，许多学者在这方面已经做了大量工作.

G·Gudendorf和J·Segers[2]通过构造Pickands相关函数得到了一些极值Copula的参数模型，并讨论了其相关系数及参数估计方法；F· Durante等[3]基于一元函数构造了一系列多元Copula族，并对它的性质进行了探究；从Copula自身出发，E·Liebscher[4]给出了两种构造非对称多元Copula的方法，并讨论了与它们相关的性质. F·Durante和G· Salvadori[5]也介绍了几种基于最近发展起来的理论构造多元极值Copula的方法，对其概率解释和模拟方法都给出了较详细的研究.

最近，R· Mesiar和V· Jágr[6]运用文献[4]中的Copula乘积构造法，得到了一类新的极值分布的尾部相关函数和Pickands相关函数，但对新构造的极值Copula的性质并没有过多讨论，本文拟将研究这种新的极值Copula的性质.

1 基本原理

1.1 尾部相关度量

在多元极值分析领域，尾部相关系数主要用来度量随机变量的尾部相关性，它是一个非常重要的概念.下面给出二元Copula尾部相关系数的定义[7].

定义1 如果一个二元CopulaC使得极限

在实际应用中，有时还需要刻画多个随机变量的尾部相关性，Copula尾部相关系数的多元形式由文献[8]给出.

定义2 设X=(X1,…,Xd)是边际分布分别为F1,…,Fd的d-维随机变量，其联合分布和Copula 分别为F和C.

1)如果对某些非空子集L⊂{1,…,d}，极限

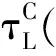
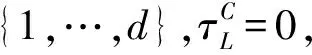
2)如果对某些非空子集L⊂{1,…,d}，极限

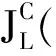
1.2 极值Copula构造

E·Liebscher[4]提出了两种构造Copula的方法，这里主要关注第一种方法，即用Copula的乘积构造新的Copula.基本原理如下：

也是一个Copula.

(1)

是一个Copula，显然，如果C1,…,Ck是极值Copula，那么由极值Copula的最大稳定性，易验证C0也是一个极值Copula.

尾部相关函数[2]是与极值Copula相关的重要概念，R·Mesiar和V·Jágr[6]给出了极值Copula尾部相关函数的构造方法，这也是极值CopulaC0的尾部相关函数的表示方法.用Ld表示所有d-维极值Copula尾部相关函数的集合.

2 主要结果

在讨论之前，首先引入两个符号，用Π表示乘积Copula，即Π(u1,…,ud)=u1…ud；用C+表示最大Copula，即C+(u1,…,ud)=min{u1,…,ud}.下面给出在一定条件下，极值CopulaC0的一个边界性质.

2.1 边界性质

定理1 给定k=2，当C1=Π时，CopulaC0的边界为：

当C1=C+时，CopulaC0的边界为：

证明：对任意CopulaC，下列不等式成立：

u1…ud≤C(u1,…,ud)≤min{u1,…,ud}，

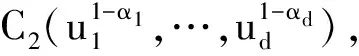
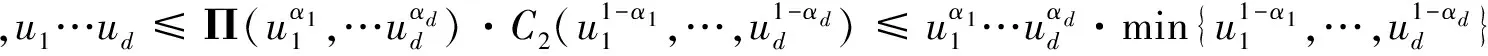
证明完毕.

当d=2时，第一种情况的上界和第二种情况的下界都属于Mashall-Olikin族，H.Li[9]对这类Copula的尾部相关性进行了更详细的讨论.Jan-Frederik Mai和Matthias Scherer[10]对第二种情况下的上界作了深入的研究，给出了BC2族的概念及更多的性质.

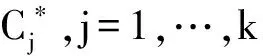
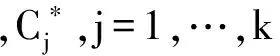
其中:xi=-ln(ui),i=1,…,d.因此，C*所对应的极值Copula的尾部相关函数为：

由尾部相关函数lj的齐次性及极值Copula与其相关函数的关系可得，C*所属的吸引场为极值CopulaC0：

2.2 上尾相关度量

本文只考虑极值分布的上象限尾部相关[2].中给出了二元极值Copula的上尾相关系数，如下：

译文：因为维诺娜的至尊十字架到哈德良长城与到怀特岛距离相等，所以罗马人把该处视为英国的中心。（先因后果）

引理3 设C是二元极值Copula，其尾部相关函数和Pickands相关函数分别为l和A，那么CopulaC的上尾相关系数为：.

λU=2-l(1,1)=2-2A(1/2)

二元极值Copula的上尾相关系数已经被广泛应用，但其更高维(维数大于2)的尾部相关系数还没有被详细讨论过，下面推导出其多元形式.

定理3 对任意d-维极值CopulaC，设其尾部相关函数为l，则C的上象限尾部相关系数为：

其中φ≠L⊂{1,…,d} ,集合L的基数L=m，且是满足1≤m

证明：对任一d-维极值CopulaC，由定义2可得

则有

以及洛比达法则，有

因此，C的上象限尾部相关系数为：

根据以上定理，我们可以很容易地得到多元极值CopulaC0的上象限尾部相关系数.

推论1 对极值CopulaC0，当非空集合I⊆{1,…,d}，|I|=2时，C0的二维边际CopulaCI的尾部相关系数为：

推论2 对极值CopulaC0，当非空集合I⊆{1,…,d}，|I|>2时， CopulaC0的上象限尾部相关函数为：

证明：当非空集合I⊆{1,…,d},|I|>2时，由定理3可得，

如果对∀i∈{1,…,d}，有αji=αj，j=1,…,k,那么

[1]NELSENRB.AnIntroductiontoCopulas[M]. 2nded.NewYork:SpringeVerlag, 2006.

[2]GUDENDORFG,SEGERSJ.Extreme-valuecopulas[C]//CopulaTheoryanditsApplications,LectureNotesinStatistics-Proceedings,Springer,Berlin--Heidelberg, 2010, 198(1):127-145.

[3]DURANTEF,QUESADA-MOLINAJJ,BEDA-FLORESM.Onafamilyofmultivariatecopulasforaggregationprocesses[J].InformationSciences, 2007, 177(24):5715-5724.

[4]LIEBSCHERE.Constructionofasymmetricmultivariatecopulas[J].JournalofMultivariateAnalysis,2008, 99(10): 2234-2250.

[5]DURANTEF,SALVADORIG.Ontheconstructionofmultivariateextremevaluemodelsviacopulas[J].Environmetrics, 2010, 21(2): 143-161.

[6]MESIARR,JAGRV. -DimensionaldependencefunctionsandArchimaxcopulas[J].Fuzzysetandsystems, 2013, 228: 78-87.

[7]JOEH.MultivariateModelsandDependenceConcepts[M].London:ChapmanandHall, 1997.

[8]LIH.Orthanttaildependenceofmultivariateextremevaluedistributions[J].JournalofMultivariateAnalysis, 2009, 100(1): 243-256.

[9]LIH.TaildependencecomparisonofsurvivalMarshall-Olkincopulas[R].WSUMathemathicsTechnicalReport, 2006.

[10]MAIJF,SCHEREM.Bivariateextreme-valuecopulaswithdiscretePickandsdependencemeasure[J].Extreme, 2011, 14(3):311-324.

[11]CHERUBINIU,LUCIANOE,VECCHIATOW.CopulaMethodsinFinance[M].NewYork:JohnWiley&Sons, 2004.

Analysis on property of a class of special extreme-value Copulas

DONG Hai-yan，LIANG Feng-zhen

( Department of Mathematics, School of science, Tianjin University, Tianjin 300072, China)

According to a class of constructed multivariate extreme-values Copula, the property of its boundary and the tail dependence measure was studied. The tail dependence parameter of extreme-value copula was also given. Under the condition that some parameters were confined, it showed that the upper tail dependence parameter of the constructed extreme-value Copula could be expressed as the covex combination of that of basic copulas.

extreme-value Copula; tail dependence function;tail dependence measure

2012-11-19.

董海燕(1989-)，女，硕士，研究方向：极值统计与Copula.

O212

A

1672-0946(2015)01-0079-04