不同水位对泵站进水池流态影响的数值模拟
2015-03-09高传昌解克宇黄丹刘新阳李郑淼
高传昌, 解克宇, 黄丹, 刘新阳, 李郑淼
(华北水利水电大学,河南 郑州 450045)
不同水位对泵站进水池流态影响的数值模拟
高传昌, 解克宇, 黄丹, 刘新阳, 李郑淼
(华北水利水电大学,河南 郑州 450045)
摘要:采用Volume of Fluid(VOF)模型对田山泵站进水池进行了三维流场计算,分析了不同水位及开机组合情况下泵站进水池的水流流态.研究发现:泵站低水位运行时,由于淹没深度较小,进水池水面存在较为剧烈的波动;进水池中水流流态发生恶化,出现了水面旋涡和水中旋涡;在附底涡和进水池两侧附壁涡的共同作用下,进水喇叭口正下方存在剧烈的旋涡,对机组的水力性能产生严重的影响.
关键词:泵站;水位;旋涡;流态;VOF模型
进水池是水泵直接从中取水的水工建筑物,其水流的流态对水泵的进水性能具有显著的影响.如果进水池内水流紊乱,出现旋涡,不仅会降低水泵的取水效率,甚至会引起机组汽蚀、振动而无法工作[1].在实际工程中,进水池的布置应满足水流顺畅、流速均匀、池内流态良好、不出现吸气旋涡和旋流的要求,保证水泵有着良好的吸水条件.因此,需要对泵站进水池进行流动计算,对进水池的流态进行研究,并改善泵站进水池的流态,保证水泵安全、高效地运行[2-3].
田山泵站位于山东省平阴县城北,从黄河取水,以供城市用水和灌溉用水,安装了12台轴流泵(含4台备用),设计提水能力24 m3/s,设计扬程7.7 m,装机容量2 520 kW.该泵站于1971年建成并投入使用.2009年,泵站采用了非连续底坎、非连续挑流消能坎和压水板3种整流措施相结合的整流方式(其中非连续底坎、非连续挑流消能坎交错布置),对由于控制闸门开度形成的淹没射流而导致的水流紊乱、流态恶化等情况进行了改造,取得了良好的效果[4].然而,由于近年来黄河水位进一步下降,泵站长时间处于低水位运行,引起了前池和进水池的流态恶化,导致水泵进水喇叭口和叶轮产生汽蚀,在检修时发现在水泵叶片的外边缘出现了断裂和蜂窝状凹坑.为探究低水位时进水池流态的变化情况及出现上述问题的原因,针对泵站低水位运行时水面波动较剧烈的现象,本文采用更接近实际情况的Volume of Fluid(VOF)模型[5]对进水池的流态进行三维流场计算研究,以期对泵站进水池的改造提供技术依据.
1数学模型
由于田山泵站中引水的含沙量低于5%,属于低浓度两相流的范畴,可以忽略泥沙对水流的影响[6],且考虑水位随时间的变化情况,所以计算时采用VOF模型进行非定常数值模拟.
VOF模型通过求解单独的动量方程和处理穿过区域的每一流体的容积比来模拟流体的运动.在每一个计算单元中,所有相的体积分数的和为1,设第q相的体积分数为αq.计算只有水和空气2相,设控制单元中水相的体积分数为α1,空气相的体积分数为α2,则有:
α1ρ1+α2ρ2=ρ,
(1)
α1+α2=1.
(2)
式中:ρ为混合流体的密度;α1、α2分别为第1相和第2相的体积分数;ρ1、ρ2分别为第1相和第2相的密度.
连续性方程:
(3)
动量方程:
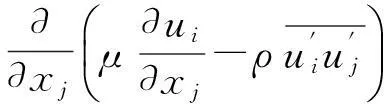
(4)
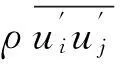
采用湍流黏性系数法使动量方程封闭:
(5)

采用RNGk-ε湍流模型使动量方程封闭,对应的湍动能k和耗散率ε的计算方程式如下:

(6)
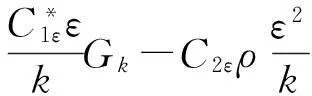
(7)
式中各项符号的具体含义见文献[7].
2物理模型及边界条件
2.1 计算区域及网格划分
田山一级泵站有防洪进水闸、前池、机房、压力水池等组成.总体布置为:沿黄河河岸线布置6孔防洪进水闸,正常设计水位34.3 m,最低水位33.7 m,闸底板高程31.0 m,防洪堤高程42.0 m;进水角度90°;防洪进水闸后接前池,长10.2 m,前池后接机房;机房与防洪进水闸平行,分上、下2层,下层为水泵进水室,上层为电动机房;2个水泵室合用1孔防洪进水闸,机房后部有水泵出水管与压力水池连接.计算区域包括1孔防洪进水闸之后的2个进水池,且为更好地反映出进水池整体来流条件及水力特性,计算区域包含了前池(包括挑流坎和底坎),具体结构如图1所示.
为了减小计算量,并满足计算精度要求,将模型划分为多个区域.规则区域采用六面体网格,个别不规则区域采用混合网格,进水喇叭口与进水管附近网格局部加密,模型总网格数量约为300万个,如图2所示.
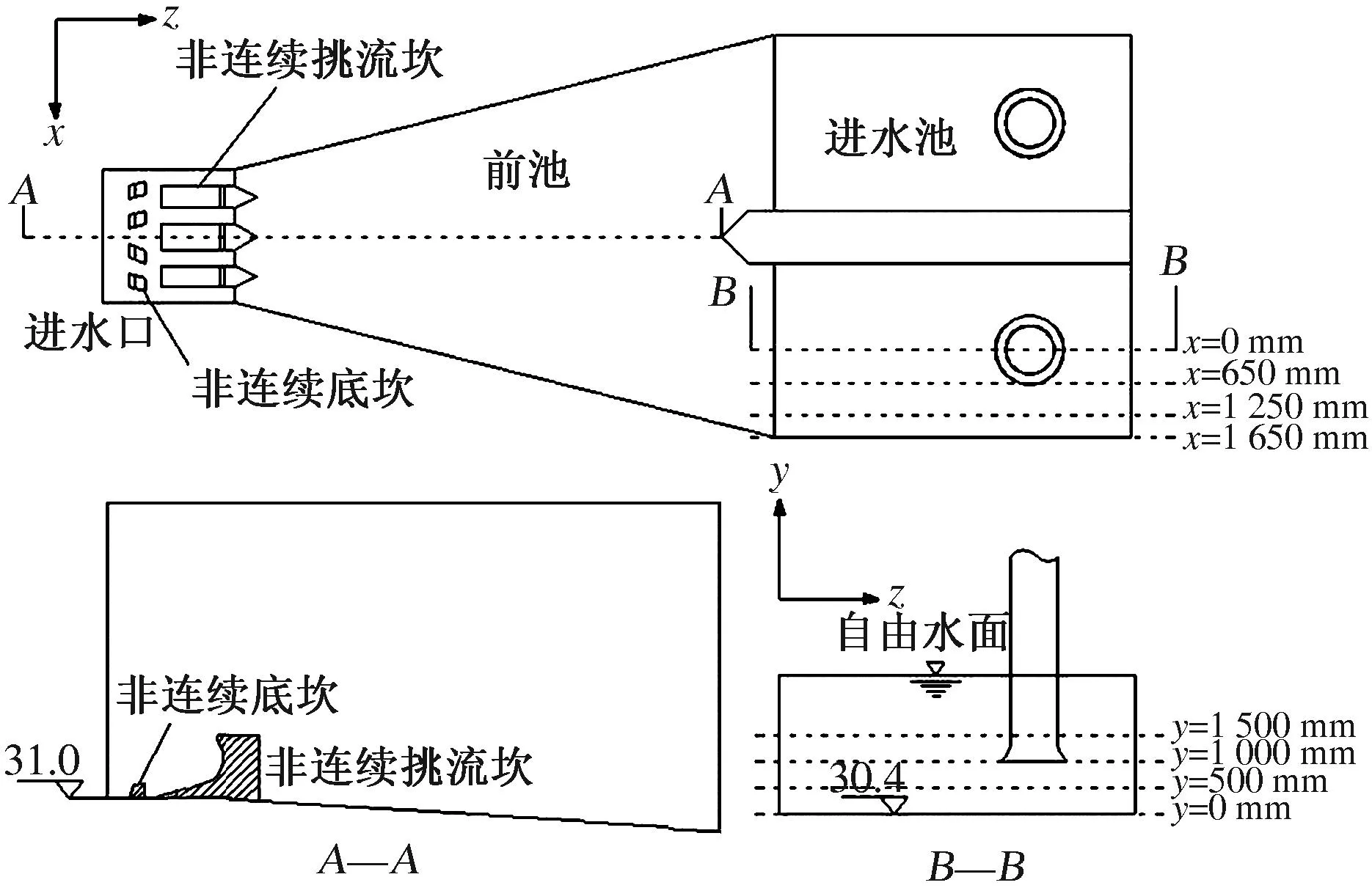
图1 前池和进水池结构及分析截面示意图

图2 计算网格示意图
2.2 边界条件和算法
进、出口边界条件均采用速度进口边界,且假定速度均匀分布,速度大小由流量和进口面积决定.进水池和前池为开敞式,水面设置为压力进口边界,其大小为1个标准大气压.壁面采用标准壁面函数法处理.进口选择3个水位:33.2、33.0、32.8 m.开机组合分为单泵和双泵,单泵流量为7 000 m3/h.
采用非定常RNGk-ε模型计算;采用有限体积法对瞬态相进行离散;压力和速度耦合采用SIMPLE算法求解;速度、湍动能等方程对流项离散均采用二阶迎风格式,时间格式为二阶隐式格式.在各速度进口边界的流量稳定且各个监控点的流速不再变化时,即可认为流场接近于长时间运行的稳定状态.
3计算结果及分析
3.1 水面动态过程分析
泵站低水位运行时,淹没深度减小.开泵之后到机组正常运行时,水面出现波动.双泵运行时水流流速增大,水面波动也较单泵更大.限于篇幅,这里仅给出了单泵运行情况下水位为33.2 m和32.8 m时进水管中心线(x=2 150 mm剖面)的水面动态高程云图,分别如图3和图4所示.从图3和图4可以看出:T=20 s之前,进水池水位波动较为明显;T=20 s之后,进水池水面趋于平稳;T=60 s时,水泵进入稳定运行状态,水面波动消失;32.8 m水位的淹没深度较33.2 m水位的更小,其水面波动也更剧烈.

图3 水位33.2 m时进水管中心线的水面动态高程云图

图4 水位33.8 m时进水管中心线的水面动态高程云图
3.2 水面流态分析
右侧进水池在单泵和双泵运行情况下(不同水位)的水面流态矢量分别如图5和图6所示.可以看出:虽然双泵开启时的水面波动较单泵剧烈,但稳定运行之后的水面流态大致相同;33.2 m水位时没有出现表面旋涡,其余2个水位时均出现了不同程度的表面旋涡,且旋涡主要分布在进水管周围.这是由于当进水管口淹没深度较小时,流量没有发生变化,造成池中表层水流流速增大,水流紊乱,较易在进水池中后部出现表面旋涡.

图5 单泵运行时的水面流态矢量图
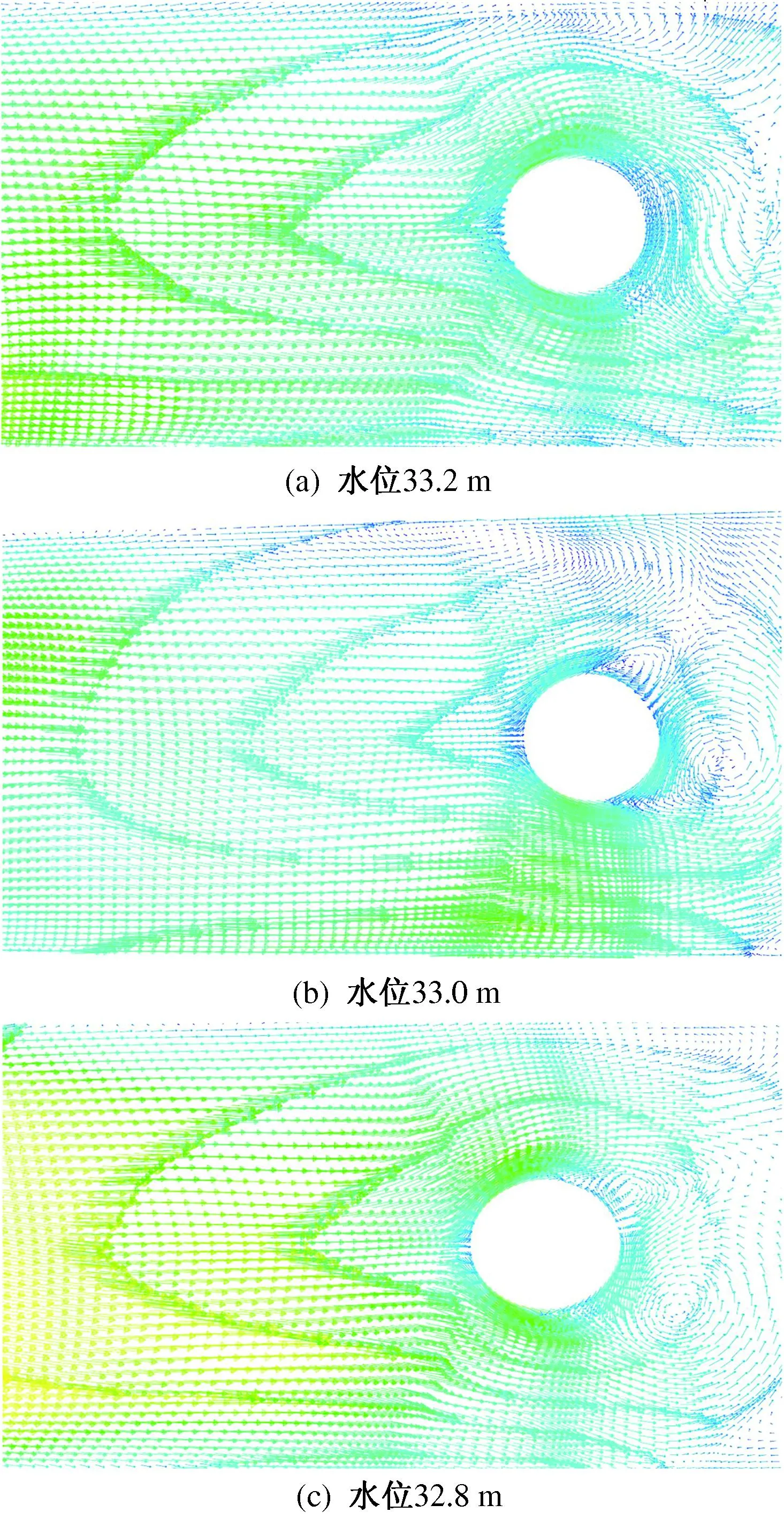
图6 双泵运行时的水面流态矢量图
3.3 y剖面流态分析
剖面分析主要是分析在低水位条件下水中旋涡的位置、类型.模拟中发现,在各个水位及开机组合情况下均出现水中旋涡,且旋涡的类型和位置相似.现就水位33.0 m、单泵运行情况进行剖面分析.
y=1 500 mm剖面距水面0.6 m,y=1 000 mm剖面为进水喇叭口所在平面,y=500 mm剖面为进水喇叭口和池底之间的中面,y=0 mm为进水池底所在的平面.各剖面的速度矢量如图7所示.从图7中可以看出:y=1 500 mm剖面存在着水中旋涡,主要分布在进水管的周围,尤以进水管到进水池后墙之间最多;y=1 000 mm剖面中进水管到后墙之间的旋涡消失,进水管前方的旋涡仍然存在;y=500 mm、y=0 mm剖面位于喇叭口的下方,在喇叭口的正下方出现了水中旋涡和附底涡,该旋涡引起了喇叭口内的流速分布不均,使叶轮叶片外缘压力降低,最终产生严重汽蚀,叶片出现蜂窝状凹坑和断裂.
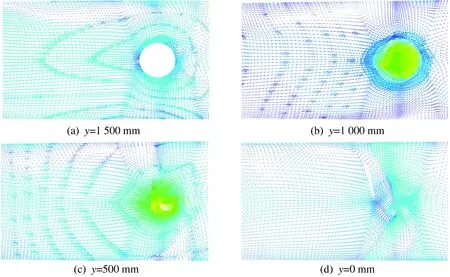
图7 进水池y剖面速度矢量图
3.4 x剖面流态分析
x=0 mm剖面为进水管道中心线所在平面,x=650 mm剖面为进水喇叭口右侧边线所在平面,x=1 250 mm剖面为进水喇叭口和右侧边壁之间的中面,x=1 650 mm为进水右侧边壁所在的平面.各剖面的速度矢量如图8所示.

图8 进水池x剖面速度矢量图
从图8中可以看出:进水管的中心剖面(x=0 mm)没有出现旋涡;在其余3个剖面均出现了旋涡,且旋涡位置基本处于与来流方向垂直的同一条直线上,可认为是同一旋涡;边壁处出现一大一小2处附壁旋涡,原因是进水池边壁处的水流存在着较大的流速梯度和水流分离现象,但随着离边壁距离的增加,旋涡逐渐减小,在进水喇叭口的下方时,小旋涡消失,大旋涡仍然存在并延伸到进水管内部.
4结语
本文运用VOF模型对田山泵站前池和进水池进行了三维流场计算,分析了在不同水位及开机组合时的进水池的流态,得到了以下结论:
1)在各工况下,由于进水池淹没深度偏小,进水池前端水流流速分布不均,泵开启之后的水面都存在着波动,水位越低,波动越剧烈;相同水位下,双泵开启时的水面波动比单泵大.
2)33.2 m水位时的淹没深度较其他2个水位的深,其水面流态相对平缓,没有出现水面旋涡;33.0 m水位和32.8 m水位时则出现了水面旋涡.
3)进水池两侧边壁均存在附壁旋涡,该旋涡一直延伸到喇叭口内;单泵运行时的进水池池底旋涡大于双泵运行时的池底旋涡,且该旋涡正对喇叭口下方并延伸到喇叭口内;进水管至进水池后墙之间存在旋涡,但后墙无附壁旋涡;在附壁旋涡和池底旋涡共同作用下,进水池池底至喇叭口之间存在较为剧烈的旋涡.
参考文献
[1]栾鸿儒.水泵及水泵站[M].北京:中国水利水电出版社,1993:216-217.
[2]何耘.水泵进水池旋涡研究的主要进展[J].水力发电学报,2004,23(5):92-96.
[3]马涛,樊红刚,袁义发,等.基于VOF模型的泵站进水池流场计算研究[J].水力发电学报,2013,32(6):244-255.
[4]高传昌,刘新阳,石礼文,等.泵站前池与进水池整流方案数值模拟[J].水力发电学报,2011,30(2):54-59.
[5]Hirt C W,Nichols B D.Volume of Fluid(VOF)method for the dynamics of free boundaries[J].Journal of Computational Physics,1981(39):201-225.
[6]刘新阳,高传昌,石礼文,等.泵站前池与进水池整流数值模拟[J].排灌机械工程学报,2010,28(3): 242-246.
[7]王福军.计算流体动力学分析:CFD软件原理与应用[M].北京:清华大学出版社,2004:120-126.
(责任编辑:陈海涛)
Numerical Simulation on the Effect of the Different Water Level on
Flow State of Intake Sump of Pump Station
GAO Chuanchang, XIE Keyu, HUANG Dan, LIU Xinyang, LI Zhengmiao
(North China University of Water Resources and Electric Power, Zhengzhou 450045, China)
Abstract:The Volume of Fluid(VOF) model is used to conduct three-dimensional flow field calculation of intake sump of Tianshan pumping station, and the flow state of intake sump of pump station is analyzed under the condition of different water level and power combinations. The results show that: when pumping stations run at a low water level, since the submerged water depth decreases, there is more severe fluctuations on the water surface of the intake sump; furthermore, since water flow state in the intake sump occurs deterioration, there has been free surface vortex and vortex in water. Finally, in the joint action of bottom-attached vortex and sidewall-attached vortex, strong vortex appears just below the bell mouth, which will have a serious impact on the hydraulic performance of water pump set.
Keywords:pumping station; water level; vortex; flow state; numerical simulation; VOF model
文献标识码:A
文章编号:1002-5634(2015)06-0010-05
中图分类号:TV131
DOI:10.3969/j.issn.1002-5634.2015.06.003
作者简介:高传昌(1957—),男,河北邯郸人,教授,博导,博士,主要从事水利水电工程方面的研究.
基金项目:国家自然科学基金项目(51309099);水利部公益性行业专项(201201085);华北水利水电大学创新计划(HSCX2014118);华北水利水电大学创新课题(YK2014-14).
收稿日期:2015-09-01
