抽水蓄能电站继电器故障机理及可靠性分析

冯凌云

(广州蓄能水电厂,广东 广州 510950)



抽水蓄能电站继电器故障机理及可靠性分析

冯凌云

(广州蓄能水电厂,广东 广州 510950)

摘要：继电器是二次回路上的重要元件，在蓄能电站中应用广泛，数量巨大，其运行状况直接关系到电厂的安全稳定运行，因此有必要对其故障模式和可靠性进行详细分析并制定相应的维护对策.以广州蓄能水电厂A厂近年来的继电器故障情况为例，通过对故障模式的详细分析,明确了蓄能电站中继电器失效的主要形式，并应用威布尔分布理论对继电器的可靠性进行了评估.根据评估结果，提出了一种基于可靠度寿命的蓄能电站继电器的维护策略，经广州蓄能水电厂的实践应用，结果表明，其维护效果较好.

关键词：抽水蓄能;继电器;故障机理;可靠性;维护策略;威布尔分布;浴盆曲线;平均秩次法

抽水蓄能电站在二次控制回路中使用了大量的继电器应用于机组的保护与控制，以广州蓄能水电厂(以下简称广蓄)A厂为例，单台300 MW可逆式抽水蓄能机组仅用于机组控制的继电器就多达300余个.该厂自1993年投产以来，随着运行时间的增长，由继电器导致的机组故障愈加频繁.因此，如何保证继电器的可靠性，确保机组安全稳定运行，已成为研究者关注的焦点.本文通过分析广蓄A厂继电器的故障模式及原因,明确继电器失效的主要形式，并利用威布尔分布模型，联合最小二乘法及平均秩次法，得到继电器可靠性分析模型和评估标准，据此提出一种维护策略并予以应用，以期为电站的安全稳定运行提供保证.

1继电器故障数据统计

继电器在蓄能电站中应用广泛，种类繁多.按照封装形式不同，继电器可分为不能打开外壳的全密封式、能够打开外壳的封闭式和不多见的无外壳的敞开式[1].依据安装方式来划分，主要有固定式和插拔式两类.固定式继电器的接线端子和继电器设计在一个本体上，维护时需要解接线.插拔式继电器配有底座，回路接线固定在底座上，继电器插拔方便，易于维护.按照使用功能分类，继电器又可分为启动继电器、中间继电器、双稳态继电器、时间继电器等几类.广蓄A厂二次控制回路中主要使用的是MTI厂的封闭式可插拔的中间继电器、双稳态继电器和时间继电器.

统计2002年至2014年13 a间广蓄A厂的故障继电器，并按照故障后果对继电器故障总数进行统计,结果见表1.

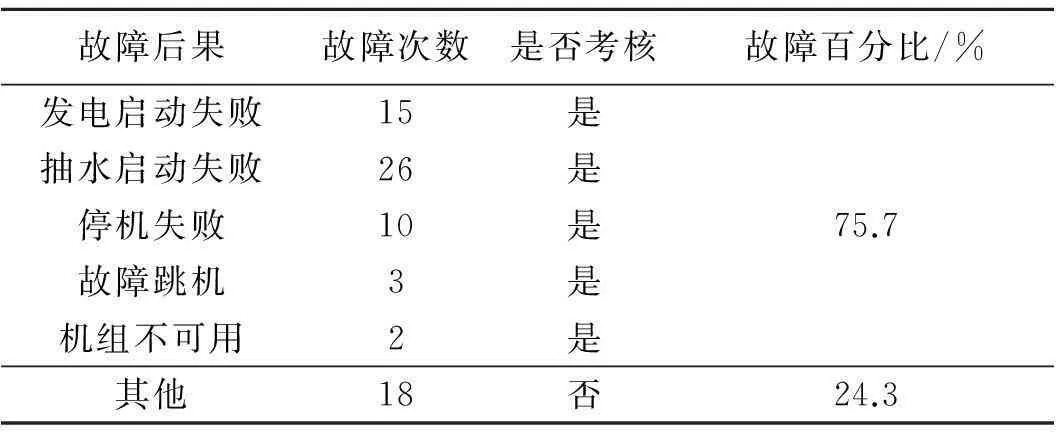
表1　继电器故障后果数据统计

由表1知，在这13 a机组运行期间共发生了74次继电器故障.根据中国南方电网有限责任公司2014年版电力事故事件调查规程要求，1台机组非计划停运(失去备用状态)4 h以下定性为电力生产安全五级事件[2].表1中导致蓄能水电机组发电启动失败、抽水启动失败、停机失败、故障跳机、机组不可用等可能产生考核事件的继电器故障次数高达56次，占故障总数的75.7%.继电器故障对机组的影响不产生考核事件的次数为18次，仅占故障总数的24.3%.由此可见，继电器是否可靠工作关系到电厂的安全稳定运行，有必要对继电器的故障原因进行分析并制定有效的维护策略.

按照继电器类型对故障总数进行统计，结果见表2.从表2中可以看出，全厂各控制系统在用的普通中间继电器总数为1 522个，时间继电器总数为146个，双稳态继电器总数为71个.经过分析可知，虽然普通中间继电器的故障次数最多，共53次，但只占该类继电器总数比例的3.5%；时间继电器与双稳态继电器的故障次数较少，分别为12次和9次，占该类继电器总数的比例分别达8.2%和12.7%.

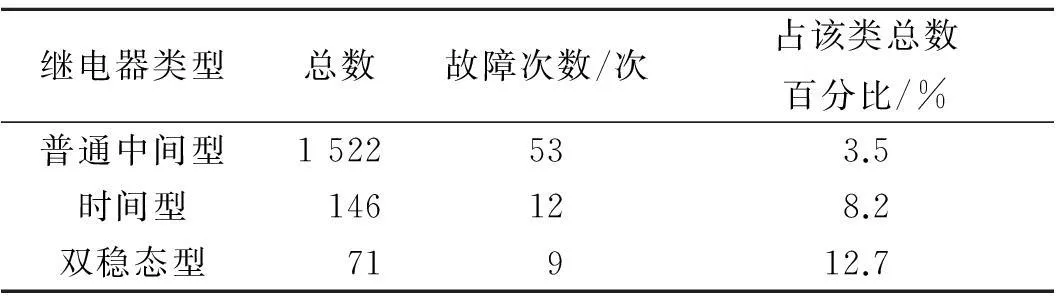
表2　继电器故障统计结果

对故障继电器的故障类别进行分析，结果见表3.由表3可以看出：继电器接触电阻异常的故障最多，共发生54次，占总数的73%；其次是接线或底座松动，共17次，占总数的23%；线圈损坏的故障次数最少，共发生3次，只占总数的4%.

表3　继电器故障类别数据统计

2继电器故障机理分析

经分析，蓄能电站中继电器的故障失效模式可分为外因失效和内因失效.所谓外因失效，是指故障原因不是由继电器本体故障导致的失效，如接线松动或底座松动等引起的失效.所谓内因失效，是指由继电器本体故障导致的失效，如线圈损坏、接触电阻异常等引起的失效.蓄能电站中继电器在一个动作周期内的失效模式、失效机理分类如图1所示.

图1　继电器动作周期内失效模式和失效机理示意图

2.1　外因失效的机理分析

外因失效的主要表现形式是接线松动和底座松动，根据经验，主要原因是人为因素和环境因素导致的.定期检查继电器时未检查和紧固接线、底座，工作结束后未将解掉的接线正确回接，是主要的人为因素；而环境因素主要是机组长期运行产生的振动冲击引起底座与继电器的脱离以及导线的松动.

2.2　内因失效的机理分析

由触点失效引起的该合不合和该断不断失效是继电器内因失效的主要形式.文中将触点失效引起的该合不合失效称之为断开失效,触点失效引起的该断不断失效称之为粘接失效.按发生失效时的触点类型不同，可将断开失效分为静合分断失效和动合分断失效2种.静合分断失效为释放过程中动触点和静合静触点不能可靠闭合;动合分断失效为吸合过程中动触点和动合静触点不能可靠闭合.粘接失效分为静合粘接失效和动合粘接失效2种.静合粘接失效为吸合过程中动触点和静合静触点不能可靠分断;而动合粘接失效为释放过程中动触点和动合静触点不能可靠分断.无论断开失效还是粘接失效均会导致继电器的接触电阻异常，引起机组控制回路功能故障.另外，若线圈出现损坏或无法励磁，将会导致继电器吸合失效或释放失效.

从电路特性、环境因素、产品设计因素、寿命因素等对内因失效原因进行分析.

2.2.1电路特性

1)引发触点发生静合分断或动合分断失效的原因，主要有燃弧过程中触点材料喷溅后净损失导致的触点不断磨损，以及触点表面聚集生成的污染膜引起的接触电阻偏大等.

2)引发触点静合粘接或动合粘接失效的机理有2方面：一方面是由于弹跳或分断电弧引起的动熔焊，当熔焊产生的熔焊力大于触点的分离力时，发生粘接失效；另一方面是由于燃弧引起的材料转移效应，包括材料堆积导致触点间隙堵塞(桥接)以及形成针刺、凹坑，使得触点无法可靠分断[3].

2.2.2环境因素

1)广州市大气环境湿度大、盐分大、粉尘多，使触点受到污染，引起触点接触不良.

2)继电器是怕热元件，排列过密，使局部温度过高，可靠性降低.

3)空气中的微小水分使电气绝缘下降,寿命缩短.

2.2.3产品设计因素

1)广蓄A厂在继电器的外壳顶部设计有排气孔，使得继电器本体更容易受到外部环境的影响.

2)时间继电器与双稳态继电器由于功能结构复杂度高，因此发生功能失效的概率较普通继电器高.

2.2.4寿命因素

1)继电器本身属于损耗型电子器件，使用寿命有限.

2)广蓄A厂继电器使用年限长，大量继电器未进行过更换.

3)蓄能机组启停频繁导致部分关键继电器频繁动作，使得线圈及触点材料磨损加快，寿命减少.

4)频繁定期检查和维护也会缩短继电器的使用寿命.

3继电器的可靠性分析

由统计数据和故障机理分析可知，触点失效是主要失效模式，应予以重点研究.由于蓄能电站中各继电器的功能作用和动作频率不同，使用年限也不相同，应根据继电器触点失效形式对继电器进行详细的寿命分析，以便制定维修对策.

3.1　威布尔分布

威布尔分布是瑞典物理学家 Weibull 教授提出的一个数学模型，目前广泛用于设备的可靠性分析，尤其适用于继电器等机电类产品的磨损累计失效的分布形式分析，且双参数的威布尔分布随着参数取值的变化可表示为失效率随时间变化的多种情况.文中采用2参数的威布尔分布来分析该蓄能电站继电器的可靠性.

威布尔分布的失效分布函数为：

(1)

故障密度函数为：

(2)

可靠度函数为:

(3)

可靠寿命为:

tr=η(-lnR)1/β．

(4)

失效率函数为：

(5)

式中：η为尺度参数；β为形状参数，代表失效模式.

如图2所示，继电器的失效率λ(t)随时间t变化的规律符合“浴盆曲线”，当0<β<1时，表明是早期失效期，失效率严格递减；当β=1时，表明是偶然失效期，失效率不变；当β>1时，表明是耗损失效期，失效率严格递增.

图2　浴盆曲线

3.2　最小二乘法的威布尔分布参数估计

目前，常用的威布尔分布参数估计法主要有[4]：图估计法、极大似然估计法和最小二乘估计法.其中最小二乘估计法操作方便且能有效实现分布函数的线性化，是威布尔参数估计的主要方法[5].

将式(3)左右变形，连续取2次对数可得：

ln[-lnR(t)]=βlnt-βlnη．

(6)

令：

x=lnt，y=ln[-lnR(t)]，

A=β，B=-βlnη．

则式(6)可化为：

Y=Ax+B．

(7)

对于线性回归方程(7)，利用最小二乘法可估算出参数[6]A和B分别为：

(8)

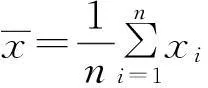
3.3　平均秩次法

用最小二乘法进行参数估计时，为了得到最佳的回归直线，关键是提高经验分布函数的精度[7].传统的经验分布函数计算方法是通过近似中位秩式(9)得到，误差较大.

(9)

式中：i为故障设备的顺序号；n为样本的总容量.

文献[8]中指出，平均秩次法是提高累计分布函数精度的有效方法，其计算公式如下[9]：

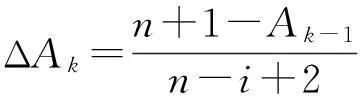
(10)

Ak=Ak-1+ΔAk，

(11)

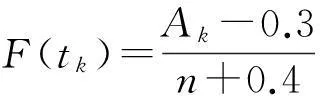
(12)

R(tk)=1-F(tk)．

(13)

式中:Ak为故障样品的平均秩次，k为故障样品的顺序号；Ak-1为前一个故障样品的平均秩次；ΔAk为平均秩次增量；i为所有样品按故障前动作次数的顺序排列号；tk为第i个样品的故障前动作次数.在故障数据已知的情况下可利用式(10)—(13)计算出一组经验可靠性指标，然后利用最小二乘法拟合回归直线，确定威布尔分布模型的尺度参数η和形状参数β.

3.4　继电器寿命的计算

使用继电器参数测试仪对广蓄A厂30个继电器样品进行10万次可靠性动作试验，在触点接触电阻不合格时停止测试，并将测试结果和分析计算过程列于表4中.

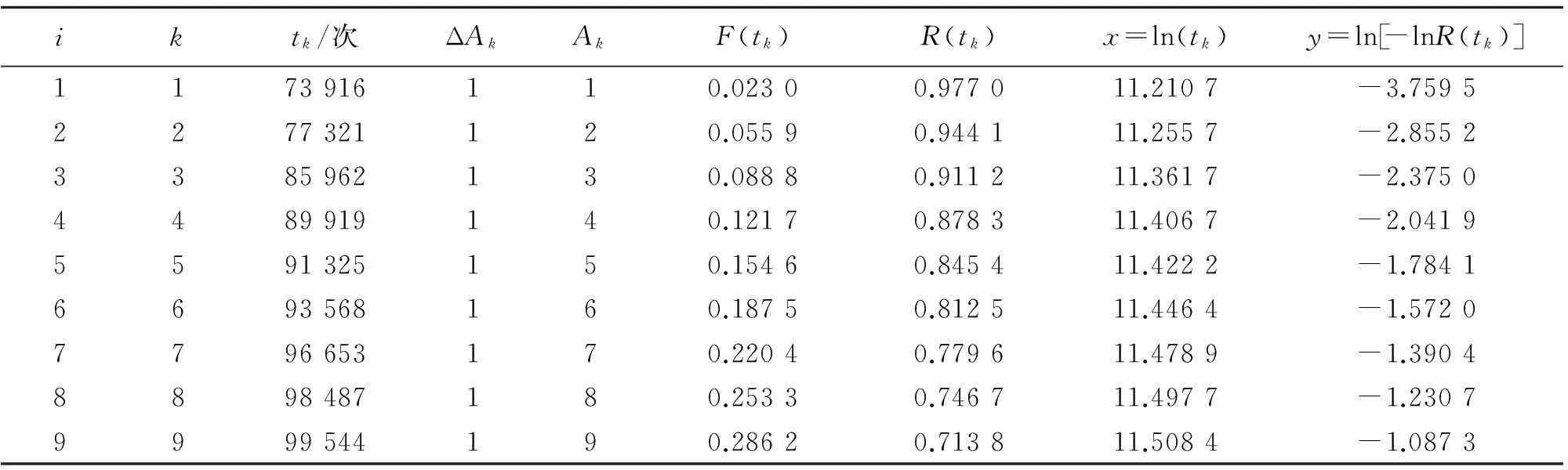
表4　平均秩次法计算继电器可靠性指标

表4中第1列为样品的时间顺序排号，第2列为故障样品的顺序号，第3列为各继电器故障时的动作次数，由于文中未发生故障的继电器均比故障继电器动作次数多，所以i和k的数值相同.试验结果显示，共有9个样品在10万次以内发生了故障.运用平均秩次法，通过式(10)—(13)计算故障继电器的平均秩次和经验分布函数值.以故障前动作85 962次的继电器为例来说明经验分布函数值的确定.

表4中x和y的值为计算出来离散点的坐标，将此坐标值代入式(8)可得回归系数A=8.122，B=-94.591，于是可知威布尔分布模型参数β=8.122，η=1.142 6.则广蓄A厂继电器的失效分布函数、故障密度函数、可靠度函数和故障率函数分别为：

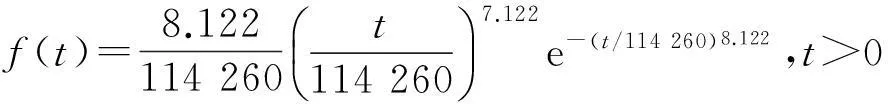
得到可靠度函数曲线如图3所示.

图3　可靠度函数图

由图3可知，β=8.122>1，继电器当前处于损耗失效期.如果取可靠度的期望值为0.99，由式(4)可得可靠寿命为tr=64 853次，如果取可靠度的期望值为0.95，则由式(4)可得可靠寿命为tr=79 266 次.

4维护策略

根据以上的分析结果，按照不同的可靠度要求，继电器表现出不同的可靠寿命，其维护策略也不尽相同.结合广蓄A厂RTU控制逻辑图，根据继电器的关键性(是否影响蓄能机组发电、抽水、停机等各工况的成功转换)及动作频率,将全部继电器分为以下4类：

1)关键高频继电器，如机组机械刹车投入命令继电器，其动作次数按照每天发电3次、抽水2次、停机5次计算，则每天动作次数为10次.

2)关键非高频继电器，如抽水工况换相刀合闸继电器，其动作次数按照每天抽水2次，则每天动作次数为2次.

3)非关键高频继电器，如一次调频动作继电器，其动作次数按照每天动作20次计算.

4)非关键非高频继电器，如尾闸油泵状态继电器,其动作次数按照每2 d动作1次，则每天动作0.5次.

期望关键继电器的可靠度为0.99，非关键继电器的可靠度为0.95，则可计算出以上各类继电器的可靠寿命，具体结果见表5.以关键高频继电器的可靠寿命计算过程为例，继电器寿命为：64 853(次)÷10(次/d)÷365(d/a)≈17.8(a).

表5　各类继电器在期望可靠度下的寿命

根据继电器寿命分析结论,结合电路特性、环境因素、产品设计因素等多方面影响，提出如下二次回路继电器维护方案.

1)关键高频继电器每个小修周期(1 a)进行1次定期检查，每个大修周期(10 a)全部更换.

2)关键非高频继电器每2~3个小修周期进行1次定期检查，每2个大修周期全部更换.

3)非关键高频继电器每2~3个小修周期进行1次定期检查，不合格者予以更换.

4)非关键非高频继电器不进行定期检查，发现故障直接予以更换.

统计2002―2014年13 a间广蓄A厂每年继电器的故障数情况，具体如图4所示.

图4　广蓄A厂继电器故障时间分布曲线

从图4中可以看出，从2006年起由于部分关键高频关键继电器与非关键高频继电器相继达到或接近其可靠寿命，故障率持续上升,到2009年左右进入故障高发密集期.2011年后,根据以上的维护策略，在大小修过程中陆续将部分继电器进行了更换，故障率开始下降.

5结语

触点失效是抽水蓄能机组二次回路继电器故障的主要模式，其失效形式符合威布尔分布.文中根据继电器样品的试验数据，利用威布尔分布模型，联合最小二乘法及平均秩次法，求得继电器可靠性分析模型，继而得到各类继电器在期望值下的可靠寿命.据此提出一种蓄能电站继电器的维护策略，经实践检验，其维护策略初见成效.目前该维护策略的水平还是处于初步阶段，以后经过长时间的研究和实践，不断给予完善，以便形成更加科学有效的继电器维修管理方法.

参考文献

[1]陈龙骧．蓄能电站二次回路继电器维护策略研究与应用[J]．水力发电，2014，40(11)：22-24．

[2]中国南方电网有限责任公司．中国南方电网有限责任公司电力事故事件调查规程：SG 210020—2014[S]．北京：中国电力出版社，2014.

[3]HAMMERSCHMIDT M,ALEXANDER R N,RIEDER W F.The effects of material transfer in relays diagnosed by force and/or voltage measurement[J].IEEE Transactions on Components and Packaging Technologies,2004,27(1):12-18.

[4]毛昭勇,宋保维,李正，等．基于遗传算法的最大似然参数优化估计[J]．机械强度，2006，28(1)：79-82．

[5]王振兴．基于威布尔分布的水利设备可靠性分析模型及应用[J]．现代电子技术，2013，36(2)：107-109．

[6]张莉,屈吉鸿,陈南祥．张家港市年径流量变化及其对气候变化的响应分析[J]．华北水利水电大学学报(自然科学版)，2015，36(1)：1-5．

[7]王桂萍,贾亚洲．MTBF分布模型的案例分析[J]．吉林工程技术师范学院学报，2005，21(3)：20-24．

[8]王博,刘媛,洪其麟，等．对军用航空发动机可靠性参数体系选择和指标确定的探讨[J]．燃气涡轮试验与研究，2003，16(2)：38-42．

[9]徐岩,白静,戴志辉．一种基于威布尔分布的继电保护装置可靠性分析的新方法[J]．华北电力大学学报(自然科学版)，2012，39(4)：15-19．

(责任编辑：杜明侠)

Failure Mechanism and Reliability Analysis of Relays in Pumped Storage Power Station

FENG Lingyun

(Guangzhou Pumped-storage Power Plant， Guangzhou 510950， China)

Abstract:The relay is an important component of the secondary circuit, and it is widely used in pumped storage power stations, and its performance is directly related to the safe and stable operation of power station. Therefore, it is necessary to analyze the failure mode and reliability, and furthermore formulate the corresponding maintenance strategy. In this paper, taking the relay fault conditions inAbranch of Guangzhou Pumped Storage Power Plant as an example, through the detailed analysis of the failure mode, the main form of relay failure in the pumped storage power plant is defined and the reliability of the relay is assessed based on the Weibull distribution theory. According to the assessment results, a maintenance strategy based on reliability life for the relay of pumped-storage plant is proposed．Through the practice in Guangzhou Pumped Storage Power Plant, the strategy has achieved an initial success．

Keywords:pumped storage power station; relay; failure mechanism; reliability; maintenance strategy; Weibull distribution; bathtub curve; average rank time method

文献标识码：A

文章编号：1002-5634(2015)06-0083-06

中图分类号：TV734.4;TK730.8

DOI:10.3969/j.issn.1002-5634.2015.06.020

作者简介：冯凌云(1960—),男,湖北武汉人,工程师,硕士,主要从事抽水蓄能电站自动化控制、嵌入式技术在电力系统中的应用方面的研究.

收稿日期:2015-09-26
创新项目：2014年中国南方电网有限责任公司职工技术创新重点项目(K-ST2014-008-13).