基于水位指数计算的下游不稳定流对水电站优化调度的影响

冯雁敏， 赵连辉， 梁年生

(1.国家电网辽宁省电力有限公司 电力科学研究院，辽宁 沈阳 110006；

2.国网新源控股有限公司 白山发电厂，吉林 桦甸 132400； 3.华中科技大学，湖北 武汉 430074)



基于水位指数计算的下游不稳定流对水电站优化调度的影响

冯雁敏1， 赵连辉2， 梁年生3

(1.国家电网辽宁省电力有限公司 电力科学研究院，辽宁 沈阳 110006；

2.国网新源控股有限公司 白山发电厂，吉林 桦甸 132400； 3.华中科技大学，湖北 武汉 430074)

摘要：为满足水电站优化运行计算在求解时间和求解精度上的要求，提出了基于水位指数规律变化假设的下游不稳定流计算方法及计算系数的确定方法.该计算方法比较简单，且有理论根据.分析了下游不稳定流对水电站最优运行方式的影响，推导了水、火电站联合优化运行时的等微增率原则公式，讨论了附增当量的物理意义及影响因素，最后提出了考虑下游不稳定流影响时的水电站运行方式的最优化原则和计算方法.

关键词：水位指数规律；下游不稳定流；等微增率原则；最优运行方式

当水电站承担调峰、调频任务时，其出力和下泄流量可能发生剧烈变化，以致在尾水及下游河道形成水位、流速急剧变动的不稳定水流.下游水位不仅与此时的下泄流量有关，还与此前时间的流量、水位等变化状态有关，且水位的变化总滞后于流量的变化，使下游水位与下泄流量的关系曲线形成了复杂的环套形.下游不稳定流的产生原因除了电站负荷发生剧烈变化的因素外，还可能与以下因素有关：梯级电站中下游电站对上游电站的回水影响；洪水期的泄洪方式变化；下游河流支流来水的不稳定性；下游综合用水部门的取水方式；潮汐作用的影响等.

下游不稳定流对水电站优化调度造成的影响包括：①下游不稳定流可能使沿途的水位和流速发生剧烈变化，使水利综合利用部门的正常运行条件遭到破坏；②对于低水头河床式水电站，因下游不稳定流造成的水位波动将引起电站水头的明显变化，直接影响电站运行的经济性，还可能使水轮发电机组产生严重的汽蚀、振动，影响电站的安全可靠运行.

下游不稳定流的计算方法有很多，有些方法理论严密，但计算复杂，不能满足电站优化调度在求解时间上的要求；有些方法计算简明，易于操作，但计算结果与实际情况相差甚远[1-3].笔者提出一种计算比较简单、有理论依据、计算结果与电站实际观测结果比较吻合的基于水位指数规律变化假设的下游不稳定流计算方法，其他用水部门的要求作为限制条件处理.

1基于水位指数规律变化假设的下游不稳定流的计算

对于水电站运行方式来说，影响最大的因素是水电站出口断面处的水位波动.许多实测资料的分析计算结果表明，水位变化可以用若干阶的常系数线性微分方程表示，根据工程计算的精度要求，高阶导数可略去不计，则水位指数的计算式可简化为：

(1)

式中：a1和b1均为常数；Zxc为不稳定流时实测的下游水位；Zx为稳定流情况下的下游水位.

式(1)为水位呈指数规律变化的微分方程.从物理意义上看，下游不稳定流是由流量的突增或突减引起的，图1为流量突增引起的水位变化曲线.

图1　流量突增引起水位变化图

在t1时刻，流量由Q1突变至Q2，下游水位首先产生突变，然后按指数规律变化，直至达到流量为Q2时的稳定下游水位Zx2.则在时刻t(t>t1),由于流量突变引起的下游水位变化AZx(t)由突变和渐变两部分组成：

1)下游水位突变部分的计算式为

AZ1=kAZx0.

(2)

式中：AZx0为流量为Q1和Q2时所对应的稳定下游水位之差，AZx0=Zx2-Zx1；k为下游水位突变系数，与河床特性有关.

2)下游水位渐变部分的计算式为

AZ2=AZx0-AZ1-AZ(t).

(3)

假设AZ(t)=AZx0(1-k)e-(t-t1)/T，则t时刻的下游水位为：

Zxc(t)=Zx2-AZx0(1-k)e-(t-t1)/T.

(4)

式中：t为流量突变时刻t1后的某一时刻；T为时间常数.

稳定状况时，下游水位Zx和流量Q间有确定的函数关系Zx(Q).故根据水电站下游的具体情况确定k和T的数值后，可计算出不稳定流时下游水位的整个变化情况.若在t1时刻，流量由Q1变至Q2，相应的稳定下游水位变化为AZx1，在t2时刻，流量由Q2变至Q3，相应的稳定下游水位变化为AZx2，则在t(t>t2)时刻由于流量突变2次，t时刻的下游水位为：

(5)

式中Zx2为t时刻的稳定下游水位.

若在时刻t之前，流量是连续变化的，利用叠加原理，可将时刻t的下游水位变化看作是无限多次小突变流量作用之和的结果，可表示为：

(6)

2下游不稳定流计算系数的确定方法

对于不同的水电站，系数T和k的数值是不同的.系数T和k的数值与下游河床的坡降、断面形状、粗糙度等一系列因素有关，很难用数学公式表示其间的关系，通常是根据某些实测资料分析计算得出.

2.1　T值的确定方法

为了计算简单，水电站停机或较长时间以某固定负荷运行时,实测下游水位的变化过程.如水电站停机过程，实测得Zx1、Zxc(0)、Zxc(1)、Zxc(2)、…、Zxc(n)、Zx2值，Zx1和Zx2为停机前、后的稳定水位.假设在t1时刻流量发生突变，而t1时刻后流量保持不变,则t1时刻后t时刻和t+1时刻的下游水位分别为：

Zxc(t)=Zx2-AZx0(1-k)e-(t-t1)/T，

(7)

Zxc(t+1)=Zx2+1-AZx0(1-k)e(t1-t-1)/T.

(8)

由于在t1时刻后流量保持不变，故Zx2+1=Zx2.取t1时刻为计算时间的起点，即t1=0，经推导得：

(9)

由各相邻时刻实测的不稳定流水位减去稳定后水位的差值，计算出T值，然后取平均值.

2.2　k值的确定方法

确定k值需要流量突变时水位突变的实测资料.

2.2.1取平均值法

令流量在t1时刻有显著的突增或突减变化，实测水位Zx1、Zxc(0)、Zxc(1)、Zxc(2)、…、Zxc(n)、Zx2的变化.t1时刻后t和t+1时刻的下游水位分别为：

Zxc(t)=Zx2-AZx0(1-k)e-(t-t1)/T，

(10)

Zxc(t+1)=Zx2+1-AZx0(1-k)e(t1-t-1)/T.

(11)

由于在t1时刻后流量保持不变，故Zx2+1=Zx2.取t1时刻为计算时间的起点，即t1=0.得到：

(12)

对多个t值的计算结果取平均值即可得k值.

2.2.2试算法

在水电站日下泄流量过程已定的情况下，实测1 d内的下游水位变化.假定几个不同的k值来计算不稳定流，可得到1 d内相应于不同k值的水电站下游水位变化过程线，将计算结果和实测结果进行比较，基于与实测结果最接近的计算水位变化过程线选取系数k的数值.

3下游不稳定流对水电站最优运行方式的影响

下游不稳定流对水电站运行方式的影响是多方面的，这里只考虑不稳定流对水电站最优运行方式的影响.不稳定流引起下游水位的变动，使水头发生改变，进而影响电站出力.

3.1　水、火电站联合优化运行的等微增率原则

水、火电站联合优化运行的目标函数为使电力系统总的费用支出最小，并以水电站日耗水量等于给定水量作为约束条件[4-6].根据此目标函数编制水电站日最优运行方式，需同时解决空间最优和时间最优问题，考虑的因素多，因素涉及面广，是一个多维、多阶的十分复杂的最优化问题.

设电力系统中只有一个水电站和一个等效火电站.系统日负荷曲线Nc(t)和水电站日用水量Wo已知.Nh(t)、N(t)分别为火电站和水电站在t时段的出力，要求找出水电站最优运行方式No(t)及火电站最优运行方式Nho(t)，使电力系统1 d的总燃料费U支出最小，即

(13)

式中u为电力系统各时刻对应的燃料费用.

假定水电站最优运行方式No(t)已经找到，现将其作微小改变，在时刻ta后Δt时段内增加水电站出力ΔNa，在时刻tb后Δt时段内减少水电站出力ΔNb.水电站运行方式作此改变后，火电站出力应作相应改变，即在时刻ta后Δt时段内火电站出力减少ΔNa，在时刻tb后Δt时段内火电站出力增加ΔNb.火电站出力改变，将引起电力系统费用的改变.由于ta和tb是1 d内任意选取的2个时刻，故最优运行方式应满足任何时刻两电站燃料及水流量耗量微增率的比值相等的原则[7-8].即

(14)

假若电力系统中有m个跨流域水电站，经类似推导可得：

(15)

3.2　λ的物理意义及影响因素

3.2.1λ的物理含义

λ的物理含义为，增加水电站单位流量所能取得的电力系统费用的节省值.故λ称为“比节约值”、“附增当量”或“动力效率”.若以电力系统火电站耗煤量最小为优化准则，则有：

(16)

式中B为耗煤率，是火电站出力Nh的函数.此时，λ的含义为水电站每增加单位用水流量相当于火电站1 h用λ吨煤，它们的发电出力相同.故λ也称为水煤当量.

(17)

λ1的含义为1号水电站增加单位用水流量的发电出力等于2号水电站增加λ1个单位用水流量的发电出力.

3.2.2λ值的影响因素

λ值与以下因素有关：①火电站和水电站的动力特性曲线；②电力系统的负荷曲线；③水电站的日用水量大小；④动力特性曲线畸形时的处理规则等.

水电站通过两条途径使火电站燃料费用减少：①承担变动负荷(调峰、调频)，改善火电厂工况条件，降低单位煤耗，减少燃料费用；②提供发电量，以减少火电厂发电量，降低燃料费用.这两个途径相互矛盾，水电站承担变动负荷越大，其调节损失越大，发电量则越小，相反，则越大.水电站日最优运行问题的实质就是，如何最好地协调解决好相互矛盾的各种问题，以使电力系统总的费用支出最小[9].λ是用以调节这对矛盾的数学因子.当水、火电站的动力特性曲线和电力系统的负荷曲线均已知的情况下，每取一个λ值，就可制定出一个最优的日运行方式，并计算出水电站相应的日用水量.假定多个λ值计算后，可得到λ与日用水量W的关系曲线λ(W).由给定的日用水量Wo即可求得对应的λ值和相应的最优运行方式.

若u′为常数，则火电站的费用与其出力成正比，当出力变化时不会带来附加的调节损失，从经济上看，由火电站担负变动负荷是有利的.水电站按固定负荷运行，以减少调节损失，充分发挥其电量效益.u′为常数时的等微增率原则就是水电站发电量最大时的运行方式应满足的最优化原则.此时，改变u′值的大小，可以改变相应的水电站日用水量，据此，可满足水电站给定日用水量的要求.若q′为常数时，按等微增率原则制定的最优运行方式必然是：电力系统的变动负荷均由水电站担负，火电站在基荷工作.

3.3　下游水位突变对水电站运行方式的影响

如果在某时刻t1，水电站流量的突变值为dQ，下位水位突变引起的水头突变值为dH，从而引起水电站出力的总变化为

(18)

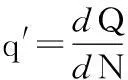
下游受不稳定流影响的水电站流量微增率为：

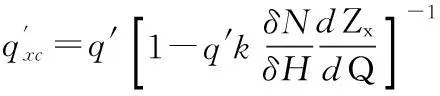
(19)

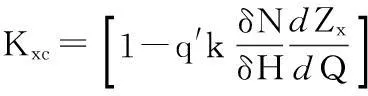
水电站下游发生不稳定流时，只需考虑流量突变引起的水位突变部分对运行方式的影响即可.水电站最优日运行方式应满足下述原则：

(20)

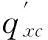
3.4　考虑下游不稳定流影响时水电站运行方式的最优化原则

对有些水电站，当下游发生不稳定流时，水位的渐变部分将对电站的运行方式产生显著影响.此时下游不稳定流不但影响水电站微增耗水率的数值，还将影响水电站最优日运行方式必须遵守的原则，尤其对于水头较低的电站，更要精确地计及下游不稳定流对其运行方式的影响.

假设已知水电站最优日运行方式、下泄流量Q(t)与下游水位Zx(t)的变化曲线.将水电站最优日运行方式作微小改变，在ta时刻后dt时段内多用水dW，在tb时刻后dt时段内少用水dW，分析由此引起的电力系统费用的变化.由于时刻ta、tb是任意选取的，所以对最优的水电站日运行方式而言，一日内的任意时刻tk都应满足下式：

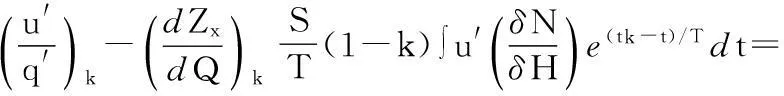
(21)

式中C为常数.

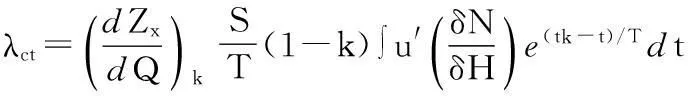
则有：

u′=(λct+C)q′.

(22)

式中：λct为计及不稳定流影响的当量，是时间的函数；q′为计及不稳定流影响的水电站微增耗水率.

式(21)、(22)即为考虑下游不稳定流影响时最优日运行方式应遵守的原则.

3.5　不稳定流影响下的水电站日最优运行方式的计算方法

在已知电力系统日负荷图及给定水电站日用水量条件下，制定水电站日最优运行方式.由于水电站的运行方式和下游不稳定流间的关系很复杂，采用逐次接近法求解.计算步骤为：

1)假定水电站某一流量过程(电站运行方式)，其日用水量等于规定值.

2)由稳定流状况的水电站下游水位-流量关系曲线求得相应的水位过程线Zx(t).

3)计算出不稳定流水位Zxc(t).

4)计算出电站水头H(t)=Z(t)-Zxc(t)，其中Z(t)为上游库水位.

5)由水电站出力特性N(Q,H)，求得出力过程线N(t).

6)由水电站微增率特性q′(N,H)，求得微增率过程线q′(t).

9)由Nh(t)=Nc(t)-N(t)，得到Nh(t).查出费用微增率u′(t).

11)计算出λc(t).

12)检查是否满足最优化原则，即

C(t)=λx(t)-λc(t)=常数.

13)若λx(t)和λc(t)之差不为常数，则需对其运行方式进行调整，并重新从第1步进行计算，直至各时段的C(t)相等时终止计算.

4结语

1)分析了下游不稳定流的产生原因及其影响，提出了基于水位指数规律变化的下游不稳定流计算方法及其计算系数的确定方法，该计算比较简单，并有理论根据.

2)推导了水、火电站联合优化运行时的等微增率原则，分析了附增当量的物理意义及影响因素，提出了考虑下游不稳定流影响的水电站运行方式的最优化原则和计算方法.

参考文献

[1]王二平,朱瑞平,张欣．某水电站工程尾水渠扩散段水力优化研究[J]．华北水利水电大学学报(自然科学版)，2015，36(1)：16-20．

[2]毛会永,罗志刚．厄瓜多尔某水电站左坝肩开挖边坡的稳定性评价[J]．华北水利水电大学学报(自然科学版)，2015，36(2)：54-57．

[3]孙东坡,李林昊,赵宝帅，等．明渠扩散段急流运动特性及调控方法研究综述[J]．华北水利水电大学学报(自然科学版)，2014，35(4)：1-6．

[4]曾勇红,王锡凡,张显．电力市场中的水电机组优化调度模型[J]．电网技术，2007，31(12)：18-22．

[5]吴至复,曾鸣,刘宝华，等．电力市场中的水火电优化调度模型及其应用[J]．电网技术，2006，30(15)：45-49．

[6]吴宏宇,管晓宏,翟桥柱，等．水火电联合短期调度的混合整数规划方法[J]．中国电机工程学报，2009，29(28)：82-88．

[7]汪新星,张明．基于改进微粒群算法的水火电力系统短期发电计划优化[J]．电网技术，2004，28(12)：16-19．

[8]王巨丰,陆俊杰．基于等微增率准则的风力水力双驱动系统最优运行方式研究[J]．电网技术，2008，32(9)：80-83,98．

[9]胡国强,贺仁睦．基于交互式多目标决策方法的水火电力系统日有功负荷优化分配[J]．电网技术，2007，31(18)：37-42．

(责任编辑:杜明侠)

Influence of Downstream Unsteady Flow Which Calculated Based on Water Level Index Rule on

Optimal Operation Mode of Hydropower Plant

FENG Yanmin1, ZHAO Lianhui2, LIANG Niansheng3

(1.Electric Power Research Institute of State Grid Liaoning Electric Power Co., Ltd., Shenyang 110006, China;

2.Baishan Power Plant, State Grid Xinyuan Holdings Co., Ltd， Huadian 132400, China;

3.Huazhong University of Science & Technology, Wuhan 430074, China)

Abstract:In order to meet the requirements of the optimal operation and computation of hydropower on the solving time and the accuracy, the calculation method of downstream unsteady flow based on hypothetic water level index rule and modulus was proposed. This calculation method is relatively simple, and there is a theoretical basis. The effects of downstream unsteady flow on the optimal operation mode of hydropower stations were analyzed and the equal incremental principle for the hydropower, thermal power station joint optimization run was derived, and the physical meaning and the influencing factors of attached modulus were elucidated. Finally, the principle and calculation method of optimal operation mode of the hydropower plant which considers the downstream unsteady flow were proposed.

Keywords:water level index rule; downstream unsteady flow; equal incremental principle; optimal operation mode

文献标识码：A

文章编号：1002-5634(2015)06-0015-05

中图分类号：TV737

DOI:10.3969/j.issn.1002-5634.2015.06.004

作者简介：冯雁敏(1984—),男,河北邢台人,高级工程师,硕士,主要从事水电站优化调度方面的研究.

收稿日期:2015-09-05