半参数与非参数可加风险模型对达菲和中药治疗H1N1流感效果的比较

曹志强王 杨李 卫

半参数与非参数可加风险模型对达菲和中药治疗H1N1流感效果的比较

曹志强1，2王 杨1△李 卫1

目的介绍半参数与非参数可加风险模型在事件发生时间分析（time-to-event analysis）方面的应用，并比较它们结果的异同。方法利用鞅方法得到半参数可加风险模型的参数估计，运用核密度估计非参数可加风险模型，用R软件进行相应的计算及统计分析。结果半参数可加风险模型中的系数相当于非参数可加风险模型可变系数的平均。相对于对照组，达菲组、中药组、达菲加中药组分别治疗53、56、29个发热病人就能多一个发热消退的病例。两个模型的生存概率图都表明，达菲、中药、达菲加中药相对不吃药都能有效治疗H1N1流感，中药与达菲的疗效相当，中西药结合的疗效最好。结论在研究者需要对风险的绝对变化进行刻画或Cox比例风险假定不满足时，可加风险模型或许是一个合适的替代。

半参数模型 非参数模型 H1N1流感

事件发生时间分析（time-to-event analysis）常用来研究风险因子与临床事件发生的联系，可选择的模型包括参数、半参数以及非参数模型。在参数模型中，常用的是加速失效模型，半参数模型主要是Cox模型，非参数模型中用的最多的是KM估计。

一个很有名但应用还不广的用来分析风险函数与协变量关系的是非参数可加风险模型［1］，1989年由Aalen提出，基本形式如下：

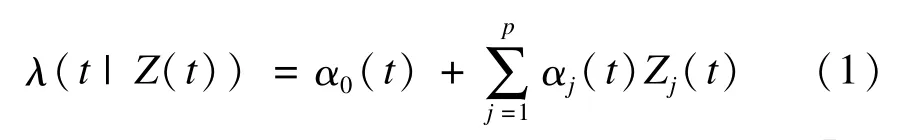
其中α0（t）是基线函数，Z（t）＝［Z1（t），…，Zp（t）］T是协变量矩阵，αj（t）是第j个协变量的回归系数，对模型（1）进一步的探讨见文献［2］。受模型（1）的启发，D.Y.Lin和Z.Ying在1994年提出了下面的半参数可加风险模型［3］：

其中β0（t）是基线函数，βj为不随时间变化的回归系数，Zj（t）是第j个协变量在t时刻的值，模型（2）进一步的扩展见文献［4］。不管是半参数还是非参数可加风险模型，回归系数度量的都是绝对风险，这点与Cox模型中的系数度量相对风险不同。因此，如果研究者感兴趣的是风险的绝对变化或Cox比例风险假定不满足时，可加风险模型或许是一个合适的替代。

资料与方法

1.资料

一项以治疗H1N1流感为目的的研究［5］，比较奥司他韦（达菲）和传统中药汤（麻杏石甘汤和银翘散加减方）的治疗效果，410例确诊为轻症H1N1流感的成年患者被随机非盲分成4组：对照组、达菲组、中药组、达菲加中药组。目标变量time为从入组治疗到结束的时间；status指发热是否消退；age是患者的年龄；g2、g3、g4是三个哑变量，分别指患者服用的是达菲、中药汤、达菲加中药；fb48h是发病至入组时间是否大于48小时的二值变量；s2、s3、s4是三个中心哑变量。为了解决结点问题，将time每个值加上［0，1］之间的随机数。

2.方法

考虑半参数和非参数可加风险模型，分析达菲和传统中药治疗H1N1流感的效果。对于半参数可加风险模型，即模型（2），当协变量与时间独立时，其形式与Cox模型类似。它们都有一个未知的基线函数，回归系数均为常数，不过Cox模型是定义在乘积尺度上，而模型（2）是定义在加性尺度上。利用计数过程中的鞅方法，借鉴Cox模型估计的偏极大似然法，可以得到模型（2）中回归系数和标准差的估计，估计的构造及大样本性质见文献［3］。

对模型（2）拟合效果的检验，可以定义类似于Cox模型中的Cox-Snell残差。比如，在观测时刻ti，假设协变量为事件发生的示性函数为δi，那么残差ri的估计为，其中若模型（2）正确，那么ri是来自标准指数分布的样本［6］。因此，我们用Nelson-Aalen估计，计算ti时刻的累积风险函数（ti），如果（ri，（ti））近似为一条斜率为1的直线，那么模型（2）正确。

模型（2）假定协变量对风险函数的影响是常数，实际上协变量的影响也可能与时间相关。从形式上来看，模型（2）是模型（1）的特殊情况，但它们参数估计的方法完全不同。在模型（1）中，直接估计回归系数是困难的，因而转向估计与其等价的累积回归系数，第j个协变量的累积回归系数定义如下：

采用非参数最小二乘法，将累积回归系数矩阵A（t）＝（A0（t），A1（t），…，Ap（t））T估计出来，估计的大样本性质见文献［1］。为了得到回归系数αj（t）的估计，需要选择合适的核函数K（x）以及窗宽b，并且利用下面的核密度估计公式：

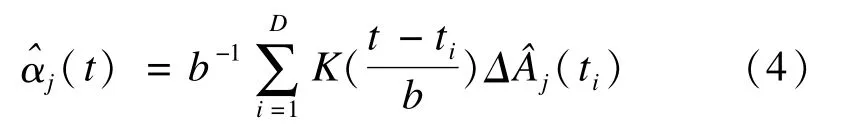
至于模型（1）拟合效果的检验，也可以定义类似的Cox-Snell残差。R软件中的timereg、ahaz包有专门分析非参数和半参数可加风险模型的程序，本文所有的统计分析结果在R 3.0.1中得到。

结 果

虽然Cox模型是分析该类问题的首选模型，但是对Cox模型的协变量进行检验时发现，变量g3（P＝0.006）、s3（P＝0.015）并不满足比例风险假定。文献［7］指出，当Cox模型的假设不满足时，可以尝试用可加风险模型进行分析。

表1是用半参数与非参数可加风险模型拟合检验的结果。在半参数模型中，除了age、fb48h、s3，其他变量都有统计学意义。控制协变量的前提下，平均来说，相对于不吃药，服用达菲的治疗为1／0.0189≈53人，说明用达菲每治疗53例H1N1流感病人就能多一个发热消退的病例。类似的，相对不吃药，服用中药汤每治疗56（1／0.0177）个病人就会多一个发热消退的病例，服用达菲加中药每治疗29（1／0.0342）个病人就能多一个发热消退的病例。通过Wald检验发现，达菲与中药汤系数之间的差别不显著，达菲加中药相对达菲或中药汤的系数差别均显著。从表1不难得知，相对对照组，三个试验组对治疗H1N1流感均有效，达菲的药效与中药汤相当，但达菲加中药比单纯达菲或中药汤的药效都要好。

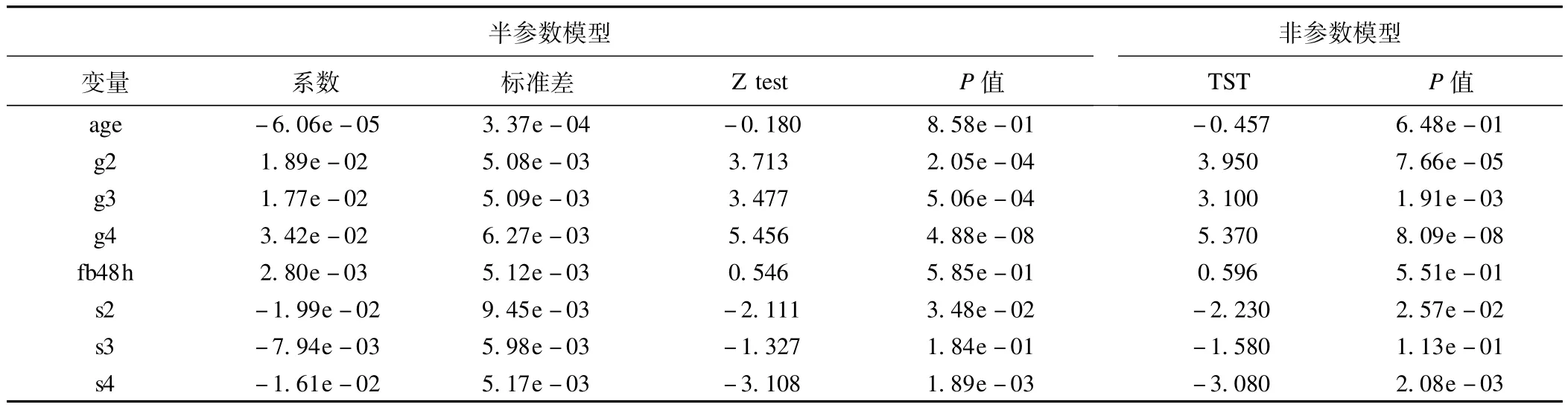
表1 半参数与非参数可加风险模型的拟合检验

非参数可加风险模型的系数随着时间变化，这里是用TST统计量及相应的P值检验变量有无统计学意义，TST的构造以及大样本性质见文献［1］。从表1还可以得到，在变量有无统计学意义方面，两个模型的结果是一样的。图1至图3是非参数可加风险模型中三组药的累积系数图以及95%的置信区间，直线是该变量在半参数可加风险模型中的累积回归系数。

图1 达菲的累积系数图及置信区间

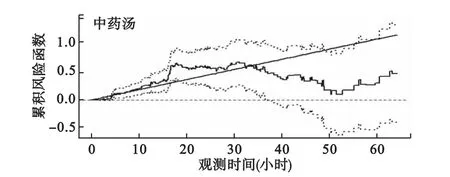
图2 中药汤的累积系数图及置信区间

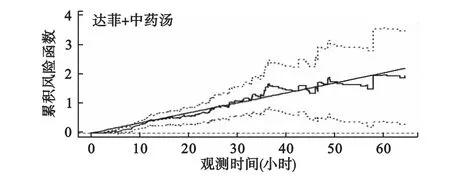
图3 达菲加中药的累积系数图及置信区间

从图1至图3可以直观地看出三组药在各个时段对风险函数的累积影响。当协变量的累积系数过了某个时刻近似平稳，则该变量不再对风险函数有影响，即该风险因子对治疗H1N1流感不再有效。从三个图还可以看出，半参数可加风险模型中三组药的累积系数在非参数可加风险模型中的95%置信区间内，实际上，其他几个变量也是如此。文献［8］指出，如果半参数可加风险模型中协变量的累积系数在非参数可加风险模型95%置信区间内，可以将非参数可加风险模型中的可变系数视为固定。

由累积回归系数，利用核密度估计可以得到回归系数。在核密度估计中，文献［6，9］表明核函数对估计结果影响不大，本文选文献中广泛应用的Epanechnikov核，窗宽的选择是用有偏交叉验证法确定。非参数可加风险模型累积系数的核密度估计见图4。

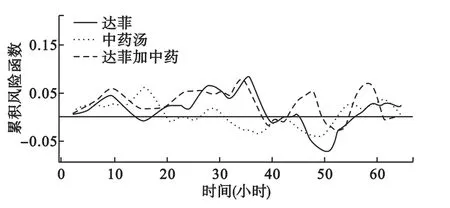
图4 非参数可加风险模型的核密度估计

图4的核密度估计展示了非参数模型中系数随时间变化的情况，其直观地说明了在控制协变量的前提下，相对不吃药，三组药在各时刻增加风险的大小。在前40小时，达菲、达菲加中药前的系数随时间变化的趋势类似，不过在前28小时达菲加中药的系数大一些。中药汤的系数与它们很不相同，尤其是12～20小时期间，达菲、达菲加中药的系数处于较低水平，中药汤的却处于较高水平。40小时后，三组药的系数波动很大，可能是由于样本量减少的缘故。从图4的纵坐标和表1中的结果发现，半参数模型中的系数是非参数模型中可变系数的平均。

图5 半参数可加风险模型的生存概率图

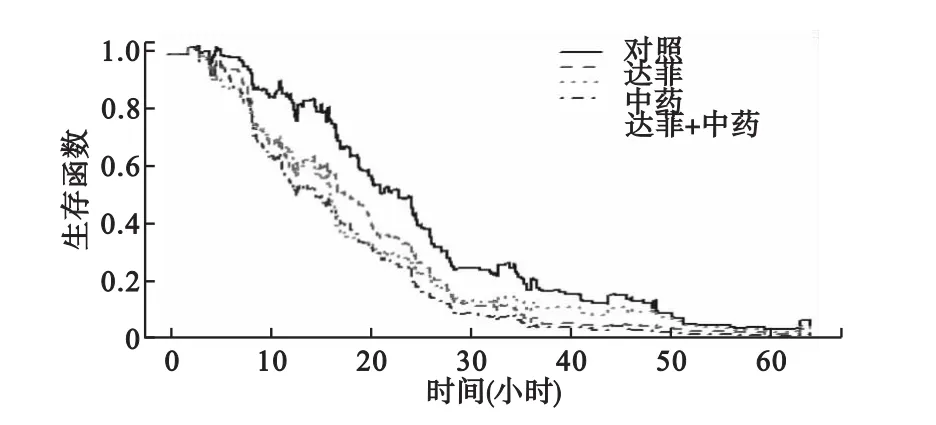
图6 非参数可加风险模型的生存概率图

图5和图6是半参数和非参数可加风险模型在其他变量的调整下，对照组、达菲组、中药组、达菲加中药组的生存概率图。两模型中三组药的疗效都比不吃药的好，达菲加中药的疗效比单纯达菲或中药汤的都要好。在半参数模型中，中药汤与达菲的疗效几乎没有差别。而非参数模型中，在前30小时中药汤的疗效稍好于达菲，30小时后达菲的疗效稍好于中药汤。

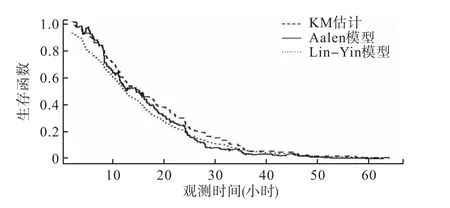
图7 达菲加中药在三个模型中的生存曲线

图7是达菲加中药在KM估计、半参数和非参数可加风险模型中的生存曲线。从图中可以看出，半参数和非参数可加风险模型的生存曲线与KM估计的差不多。文献［7］指出可以利用模型估计的生存曲线与KM估计的相比，曲线与KM估计的越相近，表明模型拟合的越好。因此，图7显示不论是半参数还是非参数可加风险模型，都较好地拟合了这组数据。

图8和图9是半参数与非参数可加风险模型的Cox-Snell残差图。相对来说，半参数可加风险模型的拟合程度比非参数可加风险模型要好。

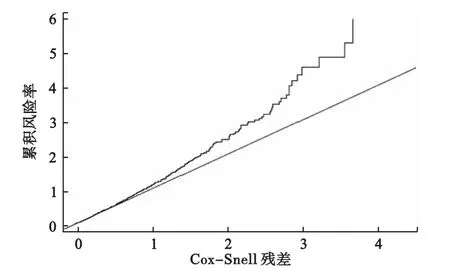
图8 非参数可加风险模型的cox-snell残差图

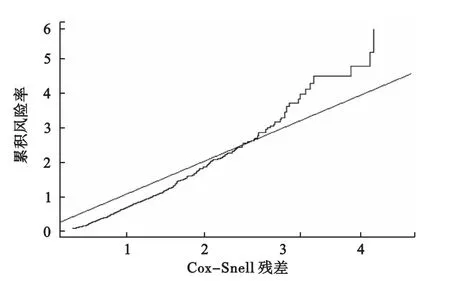
图9 半参数可加风险模型的cox-snell残差图

讨 论

本文用半参数和非参数可加风险模型研究了达菲和中药治疗H1N1流感的效果，并从参数估计、变量有无统计学意义、在其他变量调整下各实验组的生存概率、模型拟合程度等方面进行比较。在本文的例子中，两个模型中各变量有无统计学意义是类似的，半参数模型中的系数相当于非参数模型中累积系数核密度估计后的平均。相对于不吃药，达菲、中药汤、达菲加中药分别治疗53、56、29个发热病人就能多一个发热消退的病例。生存概率图则表示相对不吃药，三组药都能有效治疗甲流，达菲与中药汤的疗效相当，达菲加中药汤的疗效最好。Cox-Snell残差图表明，半参数可加风险模型比非参数模型的整体拟合效果要好。

正如预期的一样，不管是半参数还是非参数可加风险模型，其回归系数估计值都比Cox模型中的小很多。这不奇怪，因为可加风险模型与Cox模型针对不同的问题。Cox模型估计的相对风险在理解事件的关联程度方面非常有用，某种药对疾病的绝对风险影响可能较小，但相对风险仍然可以很大。如果感兴趣的是因治疗而实际获益的病例数目时，本文方法则更有优势，因为绝对风险在公共卫生规划和干预方面发挥着重要作用［10］。

若感兴趣的是协变量的平均效果，可以用半参数可加风险模型。如果想检验协变量相对于对照组的影响是否随时间变化，非参数可加风险模型是一个不错的选择。更多的文献则建议对于同一组数据，既要用Cox模型也需要用可加风险模型拟合，因为它们反映了风险函数与协变量之间两种不同的关系。文献［11］指出，即使协变量满足比例风险，Cox模型有时也会得出误导性的结果。

1.Aalen OO.A linear regression model for the analysis of life times.Statistics in medicine，1989，8（8）：907-925.

2.Aalen OO.Further results on the non-parametric linear regression model in survival analysis.Statistics in medicine，1993，12（17）：1569-1588.

3.Lin DY，Ying Z.Semiparametric analysis of the additive risk model.Biometrika，1994，81（1）：61-71.

4.Lin DY，Ying Z.Semiparametric analysis of general additive-multiplicative hazard models for counting processes.The Annals of Statistics，1995，23（5）：1712-1734.

5.Wang C，Cao B，Liu QQ，et al.Oseltamivir compared with the Chinese traditional therapy maxingshigan-yinqiaosan in the treatment of H1N1 influenza：a randomized trial.Annals of Internal Medicine，2011，155（4）：217-25.

6.Klein，Moeschberger JM.Survival Analysis：Techniques for Censored and Truncated Data.Springer，1997.

7.Abadi A，Saadat S，Yavari P，et al.Comparison of Aalen′s additive and Cox proportional hazards models for breast cancer survival：analysis of population-based data from British Columbia，Canada.Asian Pacific Journal of Cancer Prevention，2011，12：3113-3116.

8.Mckeague IW，Sasieni PD.A partly parametric additive risk model.Biometrika，1994，81（3）：501-514.

9.Aydemir，Biller.Kernel smoothing of Aalen′s linear regression model. Sonderforschungsbereich，386，1997，101.

10.Xie X，Strickier HD，Xue X.Additive Hazard Regression Models：An Application to the Natural History of Human Papillomavirus.Computational and mathematical methods in medicine，2013，796270.

11.Amato DA.A generalized Kaplan-Meier estimator for heterogeneous populations Communications in Statistics-Theory and Methods，1988，17：263-286.

（责任编辑：郭海强）

Comparison of Semi-parametric and Nonparametric Additive Hazards Models：with Tamiflu and Traditional Chinese Medicine to Treat H1N1 Flu Effect for Example

Cao Zhiqiang，Wang Yang，Li Wei（Chinese Academy of Medical Sciences，Beijing Union Medical College，National Center for Cardiovascular Diseases，Fu Wai Hospital，State Key Laboratory of Cardiovascular Disease（100037），Beijing）

ObjectiveTo introduce semi-parametric and nonparametric additive hazards models and its application in time-to-event analysis，and compare similarities and differences of the results.MethodsUsing the method of martingale to get semi-parametric additive risk model parameter estimation，using kernel density technique to estimate the nonparametric additive risk model，using R software to do corresponding calculation and statistical analysis.ResultsSemi-parametric additive hazard model coefficient is equal to the nonparametric additive hazard model of variable coefficient of the average.Relative to the control group，Tamiflu，traditional Chinese medicine，tamiflu plus traditional Chinese medicine treat53，56，29 patients respectively can be one more example of a fever subsided.The survival probability plots in two models show that，relatively to control group，tamiflu，traditional Chinese medicine，tamiflu plus traditional Chinese medicine all of three are effective in treating H1N1 influenza.Traditional Chinese medicine′s efficacy is similar to tamiflu，the efficacy of Chinese and Western medicine combined is the best.ConclusionWhen the absolute change in risk is of primary interest or when the proportional hazard assumption for the Cox proportional hazard model is violated，additive hazard model may be more appropriate.

Semi-parametric model；Nonparametric model；H1N1 influenza

1.中国医学科学院，北京协和医学院，国家心血管病中心，阜外心血管病医院，心血管疾病国家重点实验室（100037）

2.北京师范大学数学科学学院（100875）

△通信作者：王杨，Email：wangyang＠mrbc-nccd.com