自旋导弹控制耦合及补偿解耦性能研究*



自旋导弹控制耦合及补偿解耦性能研究*

贾宝1，薛林2，闫晓勇1

(1.北京电子工程总体研究所，北京100854； 2.中国航天科工集团 第二研究院，北京100854)

摘要：弹体滚转条件下，舵机的动力学滞后造成了自旋导弹的控制耦合。建立了准弹体坐标系下等效舵系统的动力学传递函数矩阵，基于串联补偿解耦方法，研究了补偿角与弹体转速、控制信号频率之间的关系，以及补偿角对舵系统关联性的影响。研究表明，针对稳态解耦补偿角取值为最优补偿角时，舵系统的通道关联性达到最小，但理论上该方法在控制信号为低频条件下才能实现近似的静态解耦；当控制信号频率较高时，会出现过补偿现象，控制系统解耦性能下降；补偿角的上界值会随着弹体转速发生变化，因此应该对补偿角进行在线动态修正，避免发生过补偿现象。

关键词：自旋导弹；控制耦合；等效舵机；对角优势度；补偿解耦；最优补偿角

0引言

舵系统是导弹自动驾驶仪中的一个重要环节，为了减小舵系统动态特性对自动驾驶仪性能的影响，在设计时通常要求其带宽为自动驾驶仪带宽的3~5倍，因此一个好的舵系统可以实现快速无静差的响应输入指令。导弹在自旋飞行条件下，弹体滚转会影响舵系统的动态性能，同时舵机的动力学滞后导致导弹的俯仰通道和偏航通道间产生了交联[1-4]。舵系统带来的控制交联通常在自旋导弹的交联项中占主要部分，一些文献中通过忽略交联项的影响，利用经典的独立自动驾驶仪设计方法对自旋导弹的自动驾驶仪进行了设计[5-7]。但有研究表明交联项将影响导弹的稳定性，使导弹的稳定边界减小[8-12]，因此，经典的驾驶仪设计方法很可能带来自旋导弹驾驶仪稳定裕度偏小的问题。

为了减小控制交联项对自旋导弹的影响，应该采用解耦方法对舵系统进行解耦控制。常见的解耦方法有对角优势法、状态反馈法、自适应解耦控制及智能解耦控制等[13]，但针对被控对象为导弹时工程实现有一定难度。文献[14]中提出了一种简单有效的解耦方法，即利用串联补偿来降低系统的关联性，但没有考虑当控制信号频率分量较为丰富时的解耦效果。本文将在这种方法的基础上，研究控制信号频率及补偿角大小对补偿前后舵系统关联性的影响，给出补偿角选取的合理范围。

1滚转条件下等效舵机分析

自旋导弹飞行过程中，舵机随着弹体一起进行滚转，其性能将会受到滚转的影响。为了对自旋导弹的伺服系统性能进行分析，首先把与弹体固连的舵机模型转换到准弹体坐标系中进行描述，为此将舵系统简化为一个一阶惯性环节[15]：

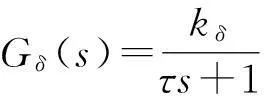
(1)

即

(2)

式中：δy1，δz1为弹体系下舵机的舵偏角；δyc1，δzc1为弹体系下舵机的输入指令信号。

设准弹体坐标系下等效舵机输出信号为δy4，δz4，输入信号为δyc4，δzc4，则根据准弹体坐标系与弹体坐标系之间的转换关系，有[16]

(3)

将式(3)代入式(2)，整理后有

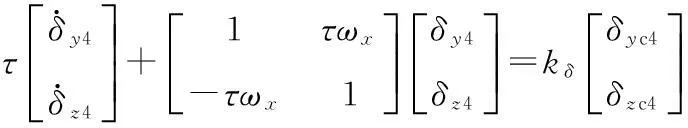
(4)

对上式进行拉普拉斯变换，可得到在准弹体坐标系下舵机系统的传递函数矩阵为

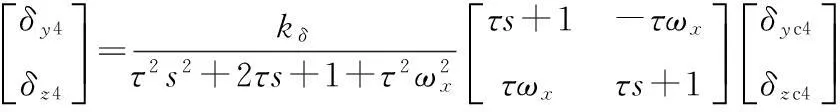
(5)

从式(5)可以看出，弹体滚转使等效舵机的阶次增加，同时次对角线上的元素表示了舵机动力学滞后引起的自旋导弹控制耦合问题，即俯仰(偏航)通道的控制信号在导弹的另一个通道产生了控制力。

定义G1δ(s)=δy4/δyc4=δz4/δzc4为主通道舵机传递函数，将其进行变形，得到标准形式为

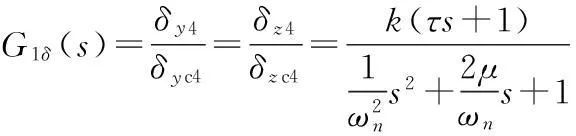
(6)

式中：

弹体滚转使主通道的控制增益降低。同时，等效舵系统的阻尼随着转速的增大而减小，而自然角频率ωn随着转速的增加而增加，故弹体滚转使舵机环节的平稳性变差，且转速越高，系统平稳性越差。作近似计算时，系统的带宽可表示为

ωb=(2ωn-ωs)，

(7)

式中：ωs=1/τ。可见等效舵系统的带宽将随着转速的增加而增加，即弹体转速越高，系统快速性越好。

定义G2δ(s)=δz4/δyc4=-δy4/δzc4为耦合通道舵机传递函数，它是一个二阶环节，标准形式为

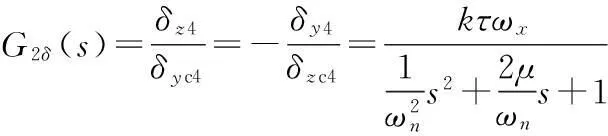
(8)

对等效舵机的传递函数进行频域分析，由式(6)得到主通道传递函数的频率特性为

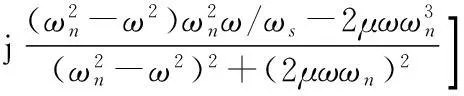
(9)

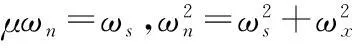
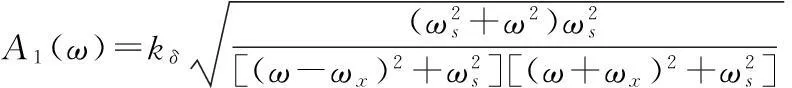
(10)

相频特性为

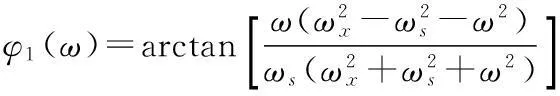
(11)

同理，可得耦合通道传递函数的幅频特性为

(12)

相频特性为

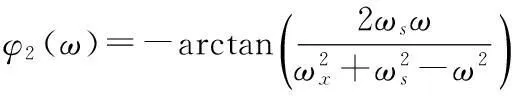
(13)

2滚转条件下舵系统的关联性分析

弹体滚转使舵系统变为一个多输入多输出系统，为了定量分析舵系统两通道间的耦合程度，可以使用对角优势度的概念来对系统的关联性进行定量描述。根据式(10)和(12)，可定义舵系统的对角优势度为

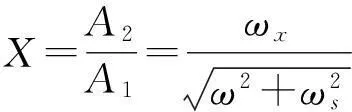
(14)

从式(14)可以看出，舵系统的对角优势度会随着弹体转速的增加而变大，同时随着舵机带宽的增加而变小。此外，对角优势度还会随着输入信号频率的增大而减小，从传递函数的幅频特性来分析，主通道传递函数G1δ受到零点的影响，使其幅频特性近似以-20 dB/dec的速度衰减，而耦合通道传递函数G2δ的衰减速度为-40 dB/dec，即A2相比于A1来说衰减的更快，则其比值也就会减小，如图1所示。

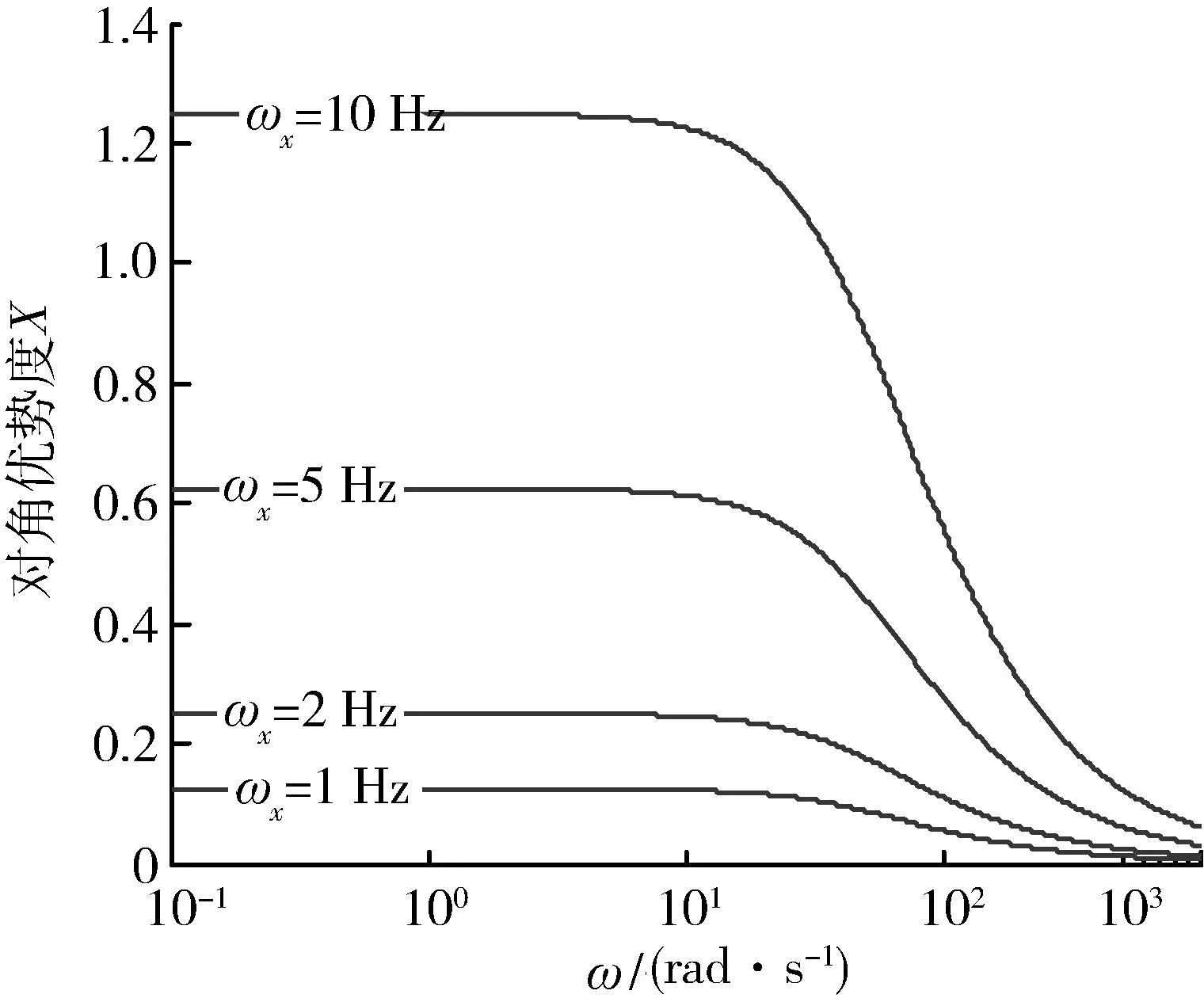
图1　舵系统的对角优势度曲线Fig.1　Dominance degree of rudder system

从图1可以看出，当弹体转速较高时，舵系统在低频段的对角优势度较大，而导弹的控制信号一般都出现在这个频段，因此有必要进行解耦控制来减小舵系统的对角优势度。一种简单且可行的方法是通过串联补偿来降低系统的关联性，甚至实现静态解耦[14]，这种解耦方法对于带宽较大的舵系统来说是有效的。设超前补偿角为φδ，满足φδ<90°，则有关系式：

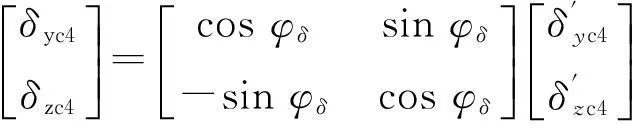
(15)

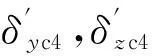
由式(5)和(15)，可得补偿后的等效舵系统传递函数为

(16)

串联补偿使主通道传递函数的带宽减小，而使耦合通道的传递函数带宽增加。利用补偿前舵系统传递函数的频率特性，即

(17)

可得补偿后舵系统传递函数的幅频特性为

(18)

相频特性为

(19)

则补偿后系统的对角优势度可表示为

(20)

补偿后的对角优势度是补偿角φδ及输入信号频率ω的函数，取定转速ωx的值，可得到如图2所示的对角优势度曲线，图中虚线为补偿前的对角优势度。

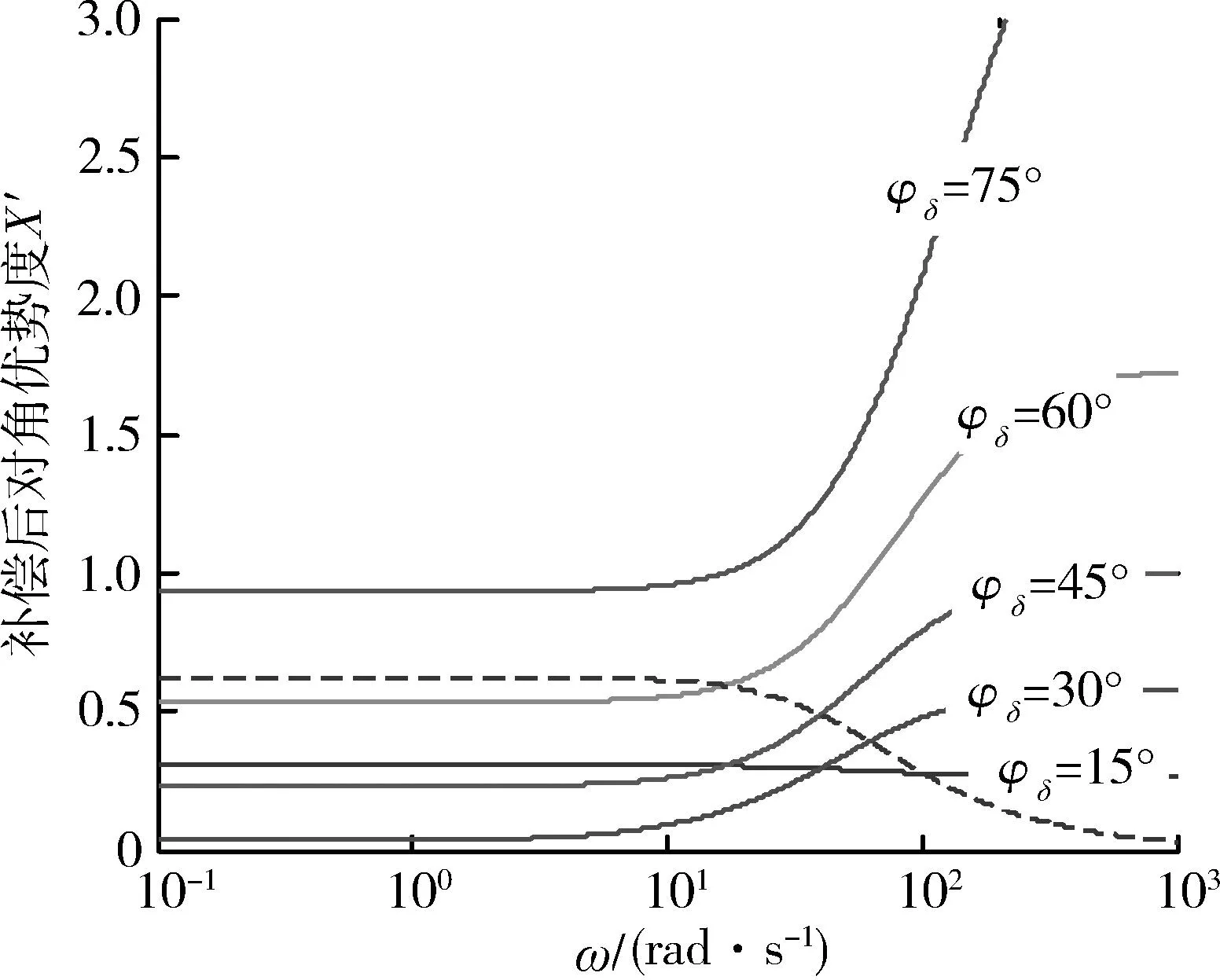
图2　补偿后的舵系统对角优势度曲线Fig.2　Dominance degree with compensation

从图中可以看出，对于固定的ω值，补偿后的对角优势度随着补偿角φδ的增大，先减小后增大，说明存在一个最优的补偿角使对角优势度达到最小，下面来求这个最优的补偿角。在式(20)两端平方后对φδ求导，可得

(1-X2)tanφδ-Xcos(φ1-φ2)].

(21)

上式的分母项一定为正，下面来分析其分子项，设

f(a)=Xcos(φ1-φ2)a2+(1-X2)a-Xcos(φ1-φ2)],

(22)

式中：a=tanφδ。这是一个关于a的二次方程，由传递函数G1δ和G2δ的相频特性可知，φ1-φ2的最大值为π/2，即式(22)中二次项的系数为正。对式(22)进行求解，得

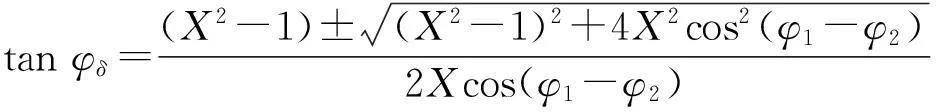
(23)

式(22)的2个根为一个正根和一个负根，由二次函数的性质可知，当tanφδ取正根时，X′有最小值，符合图2中对角优势度对补偿角φδ的变化规律。当输入信号频率ω为0时，有φ1-φ2=0，此时使对角优势度取最小的补偿角为

(24)

将其带入式(20)后可得X′=0，即实现了静态解耦。由式(20)还可知，只有当ω为0时，对角优势度才有可能为0。而对于ω不为0的情况，对角优势度永远不为0，此时的最优补偿角为

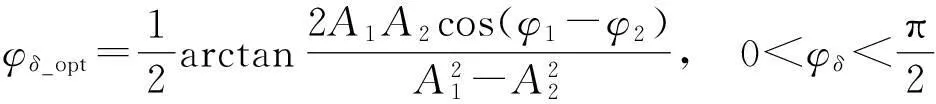
(25)

当输入信号频率逐渐变大时，cos(φ1-φ2)将逐渐接近于0，则最优补偿角也将逐渐减小并接近于0，如图3所示。进一步，利用最优补偿角得到的最优对角优势度也将接近于补偿前的对角优势度。

图3　最优超前补偿角Fig.3　Optimal leading compensation angle

从式(25)中可以看出，系统的最优补偿角与弹体的滚转速度ωx及输入信号的频率ω之间存在着复杂的非线性关系，而且在导弹飞行过程中，这2个量都在不断地发生变化且难以得到精确的测量，因此在工程实际中，很难得到最优补偿角的值并加以利用。考虑到导弹的输入信号频率较小，一般在几Hz的量级，因此一种可行的方案是采用静态解耦时的补偿角，也即是ω为0时的最优补偿角。

从图2中还可以看出，当补偿角φδ大于某一值时，补偿后的对角优势度没有降低，反而得到了增加，下面对这一现象进行理论分析。将补偿前后的对角优势度平方后相减，得

(-tan2φδX2-2cos(φ1-φ2)tanφδX+tan2φδ).

(26)

为使补偿后的系统对角优势度得到降低，应使上式等号右端的值为负。在式(26)等号右端的分数式中，分母项永远为正，故只需要分子项为负即可，即

-tan2φδX2-2cos(φ1-φ2)tanφδX+tan2φδ<0.

(27)

对这个不等式进行求解后可得

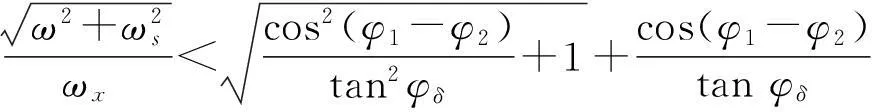
(28)

当补偿角φδ固定时，输入信号频率ω应小于某一值，否则补偿后的对角优势度将大于补偿前的。如果固定ω的值，则根据式(27)有

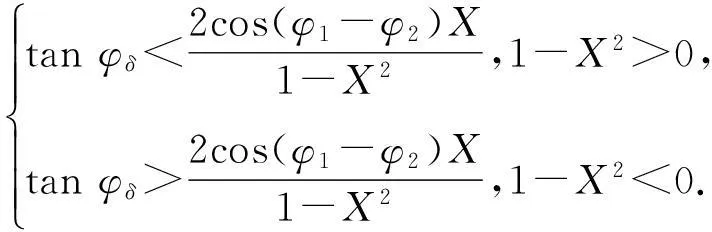
(29)

当φδ<90°时，式(29)的第2个不等式是永远成立的。当ω增大时，式(29)中第1个不等式的右边项是在减小的，即当ω为0时，其值为最大，如果此时式(29)依然不成立，即

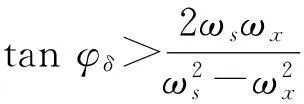
(30)

则补偿后的对角优势度在任何频率下都将大于补偿前的值。定义

(31)

为补偿角的上界值，超过这个值后，补偿解耦将造成过补偿，使系统关联性更加严重。对比式(31)和式(24)可以看出，补偿角的上界值正好是实现静态解耦的补偿角的2倍。

自旋导弹在飞行过程中，弹体转速是在不断的发生变化的，那么其补偿角的上界值也是不断变化的。将φδ_sup对ωx求导，可得

(32)

这是一个正数，可知φδ_sup对ωx是单调递增的。在实际飞行中应该对补偿角进行在线修正，如果飞行全程使用固定的补偿角，则当弹体转速降低时，可能出现补偿角大于上界值的情况，从而导致系统关联性变大。

3算例仿真

以某舵系统为例进行验证分析，设此舵系统的带宽为ωs为8 Hz，弹体的滚转速度ωx为5 Hz。在侧向输入单位阶跃信号，即ω为0，则补偿前的对角优势度为X=0.625，此时系统的响应信号如图4所示。

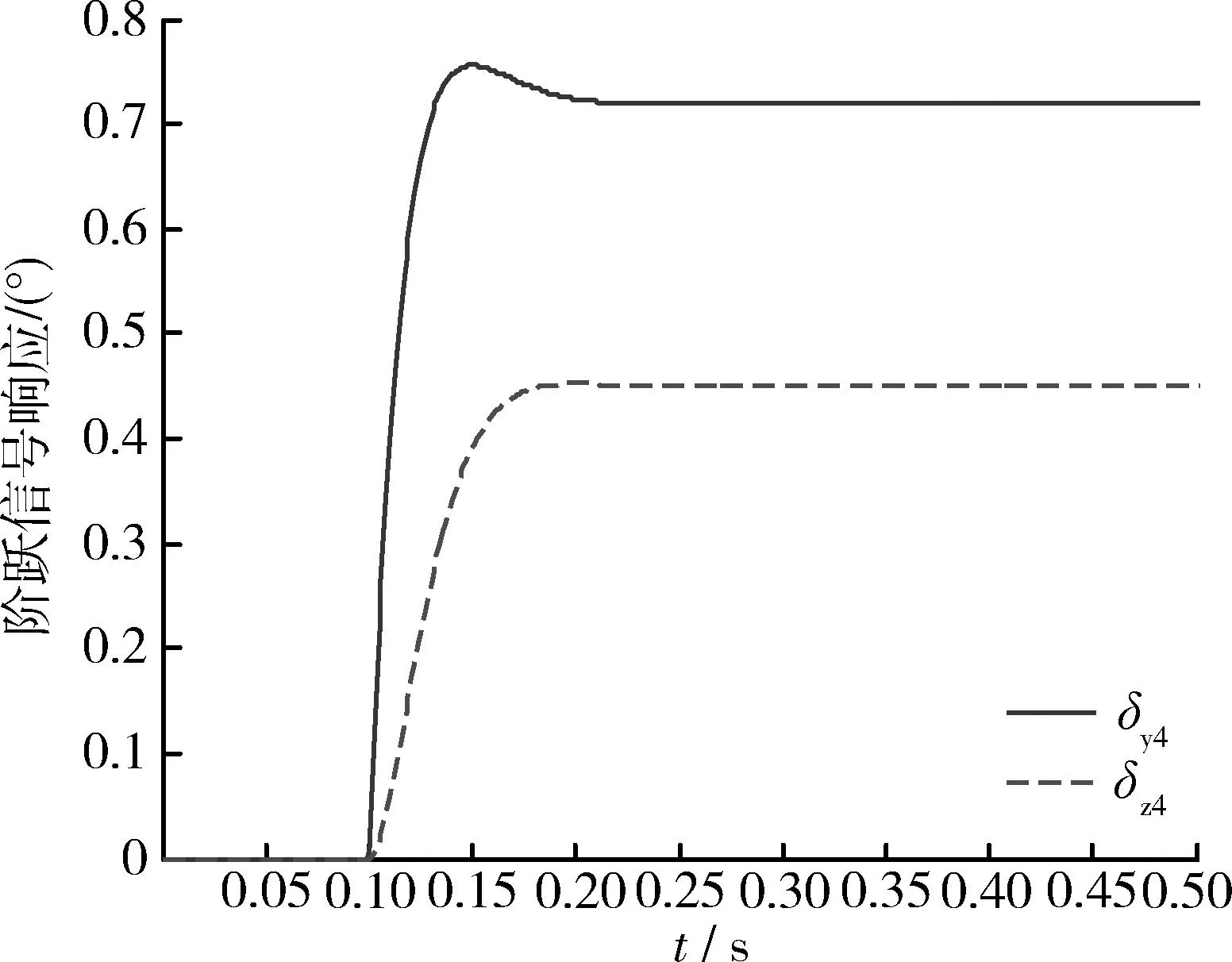
图4　补偿前系统的阶跃响应Fig.4　Step response without compensation

由式(25)可知最优补偿角为φδ_opt=32.01°，使用这个角进行串联补偿，系统实现静态解耦，如图5所示。

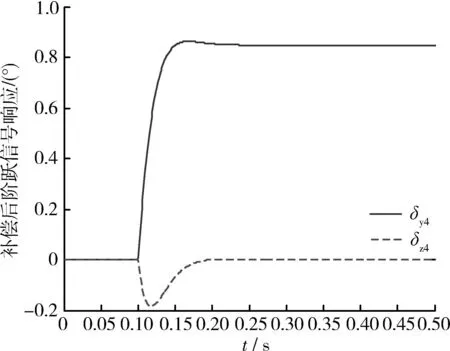
图5　最优补偿后系统的阶跃响应Fig.5　Step response with optimal compensation

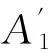
如果侧向输入信号是幅值为1，频率为2 Hz的周期信号，则补偿前的对角优势度为X=0.606 3，相比阶跃信号有所降低，此时系统响应如图6所示。

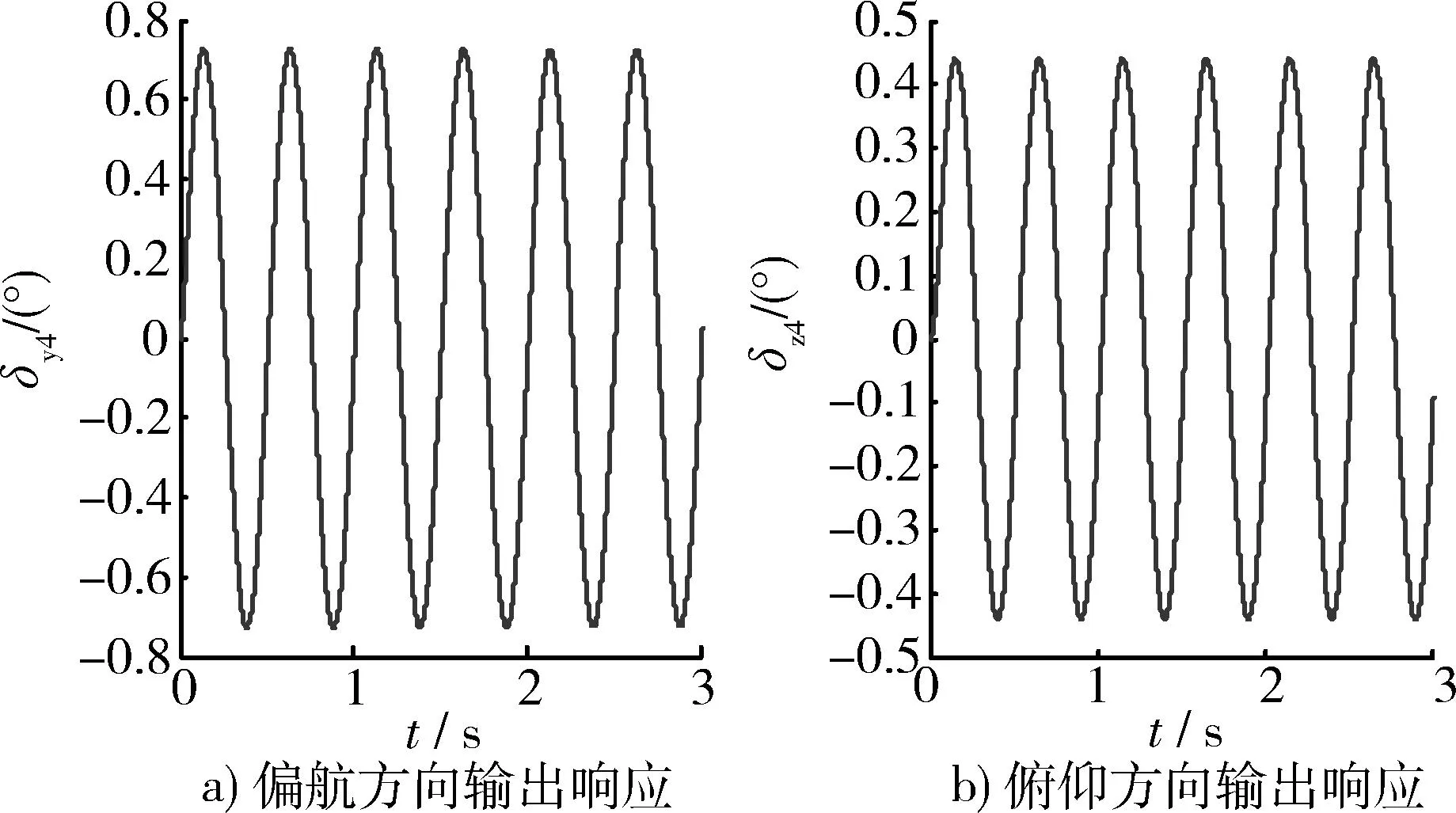
图6　补偿前系统的频率响应Fig.6　Frequency response without compensation

采用最优补偿角进行串联补偿，根据式(25)可得最优补偿角为φδ_opt=30.87°，则最优对角优势度为X′=0.109，没有达到完全的解耦，如图7所示，但此时系统关联性得到很大的降低。如果采用静态解耦时的补偿角φδ=32.01°进行补偿，补偿后的对角优势度为X′=0.110 5，略大于采用最优补偿角时的值，系统的关联性同样变得很小。

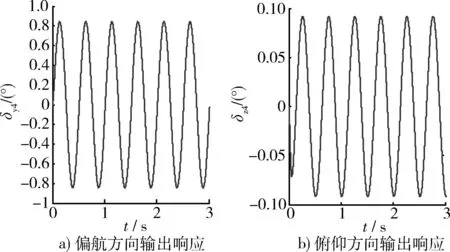
图7　最优补偿后系统的频率响应Fig.7　Frequency response with optimal compensation

如果在自旋导弹飞行过程中，不对补偿角进行在线修正，而是全程使用固定的补偿角，比如使用ωx=5 Hz，ω=0 Hz时的最优补偿角，即φδ=32.01°，舵系统的对角优势度会随着转速的不同而发生变化，如图8所示，当转速低于2.6 Hz时，系统出现过补偿的现象，关联度增加。

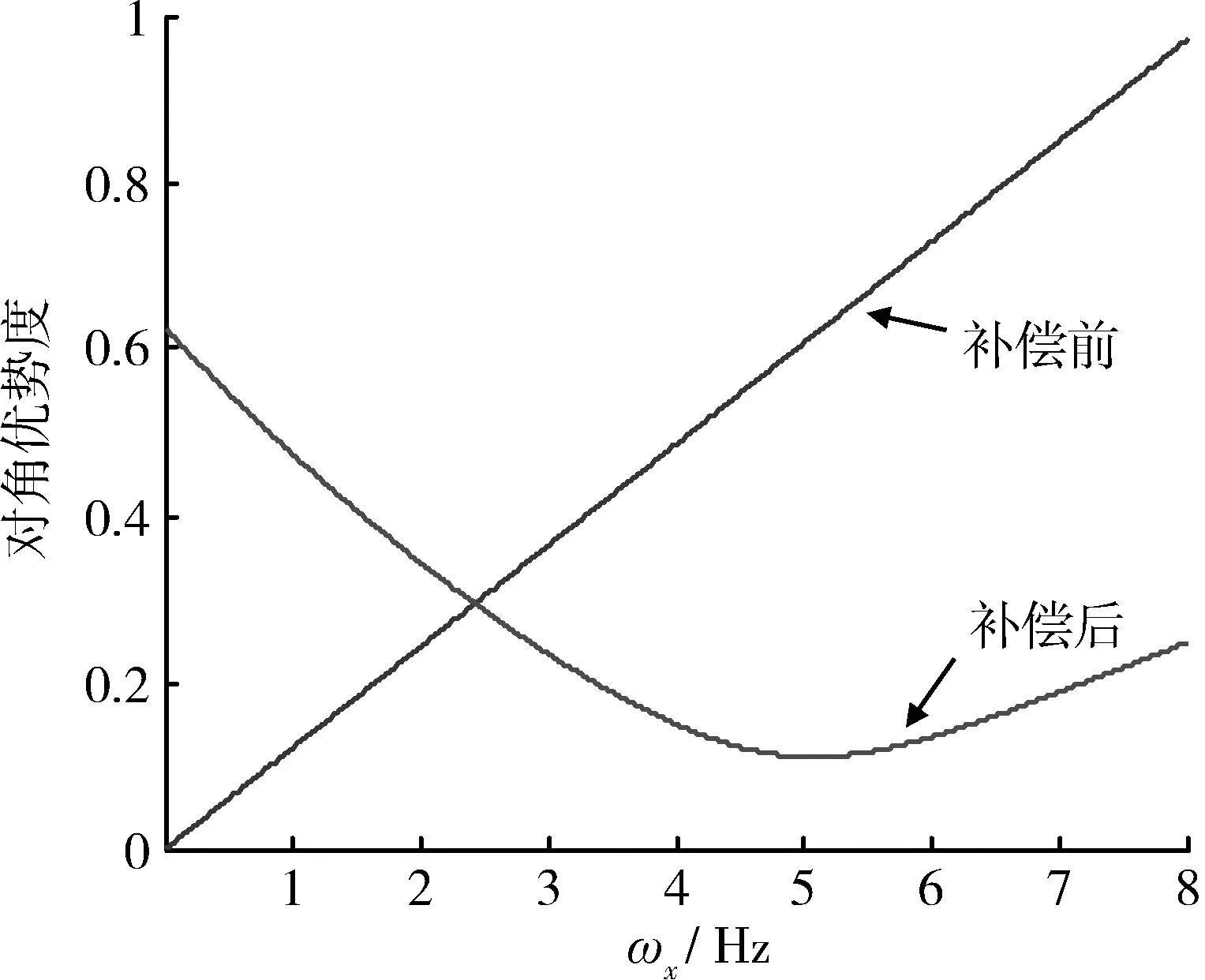
图8　对角优势度随转速的变化曲线Fig.8　Dominance degree for different rolling speeds

因此，有必要根据对角优势度对输入频率的变化情况，在串联补偿角选取时适当考虑留有一定余量，可以削弱主要工作频率区间内的过补偿现象。或者在输入信号中增加调节网络，促使信号的幅频特性与对角优势情况相匹配。

4结束语

本文对弹体滚转下舵系统的动态性能及解耦特性进行了分析。将舵系统的传递函数变换到准弹体坐标系下进行分析可知，弹体滚转不仅改变了舵系统的传递函数，使其阶次增加，而且造成了俯仰通道和偏航通道之间的交联。系统的关联性大小可以用对角优势度来表示，其值将随着弹体转速的增大而变大，同时随着输入信号频率的增大而减小。为了减小舵系统的关联性，可以采用超前补偿角进行串联补偿，当补偿角小于上界值时，这种方法可以有效减小系统的对角优势度。对于不同的输入信号频率ω，都会有一个最优补偿角与之对应，利用这个角进行补偿，所得到的对角优势度将是最小的，但只有在ω为0时才能达到完全的解耦，即对角优势度为0。自旋导弹在飞行过程中，难以对控制信号频率进行有效的测量，因此不可能始终使用最优补偿角进行补偿，一种可行的方法是使用ω为0时的补偿角，并根据转速的变化对其进行在线修正，以消除转速变化引起的补偿误差；同时考虑提前留出必要补偿余量或增加增益动态调节环节以增强解耦控制对不同频率的全局适应能力，避免过补偿现象的出现。

参考文献：

[1]LANGE B O，FLEMING A W，PARKINSON B W. Control Synthesis for Spinning Aerospace Vehicles[J]. Journal of Spacecraft and Rockets, 1967, 4(2): 142-150.

[2]袁天保，刘新建，秦子增. 自旋弹道导弹动力学与控制[J]. 宇航学报，2006，27(2)：217-221.

YUAN Tian-bao, LIU Xin-jian, QIN Zi-zeng Dynamic and Control of Spinning Ballistic Missile[J]. Journal of Astronautics, 2006, 27(2): 217-221.

[3]陈罗婧，刘莉，于剑桥. 双通道控制旋转导弹自动驾驶仪回路的数学变换及其耦合性分析[J]. 北京理工大学学报，2007，27(10)：847-850.

CHEN Luo-jing, LIU Li, YU Jian-qiao. Transform and Coupling Analysis of Double-Channel Control Rolling Missile Autopilot Loop[J]. Transactions of Beijing Institute of Technology, 2007, 27(10): 847-850.

[4]YAN X, YANG S, ZHANG C. Coning Motion of Spinning Missiles Induced by the Rate Loop[J] Journal of Guidance, Control, and Dynamics, 2010, 33(5):1490-1499.

[5]CREAGH M A, MEE D J. Attitude Guidance for Spinning Vehicles with Independent Pitch and Yaw Control[J]. Journal of Guidance, Control, and Dynamics, 2010, 33(3): 915-922.

[6]LESTAGE R. Analysis of Control and Guidance of Rolling Missiles with a Single Plane of Control Fins[C]∥AIAA 2000-3971.

[7]LDAN M, SHIMA T, GOLAN O M. Integrated Sliding Mode Autopilot-Guidance for Dual Control Missiles[J]. Journal of Guidance, Control and Dynamics, 2007, 30(4): 1081-1089.

[8]FRARY D J. The Prediction of Autopilot Behavior in the Presence of Roll Motion[R]. British Aircraft Co., Rept. ST5686, May 1971.

[9]GARNELL P. Guided Weapon Control Systems [M]. 2nd ed.New York：Pergamon, 1980:118-126.

[10]MRACEK C P, STAFFORD M,UNGER M. Control of Spinning Symmetric Airframes[R]. National Technical Information Service Rept. ADA466818, Nov. 2006.

[11]YAN X, YANG S, XIONG F. Stability Limits of Spinning Missiles with Attitude Autopilot[J]. Journal of Guidance, Control, and Dynamics, 2011,34(1):278-283.

[12]LI K, YANG S, ZHAO L. Stability of Spinning Missiles with an Acceleration Autopilot[J]. Journal of Guidance, Control, and Dynamics, 2012, 35(3): 774-786.

[13]桑保华，薛晓中. 多变量解耦控制方法[J]. 火力与指挥控制，2007，32(11)：13-16.

SANG Bao-hua, XUE Xiao-zhong. A Summary of Multivariable Decoupling Control Methods[J]. Fire Control and Command Control, 2007, 32(11): 13-16.

[14]闫晓勇，张成，杨树兴. 一类滚转弹的补偿解耦方法[J]. 弹道学报，2009，21(4)：17-20.

YAN Xiao-yong, ZHANG Cheng, YANG Shu-xin. Decoupling Technique for a Class of Rolling Missile[J]. Journal of Ballistic, 2009, 21(4): 17-20.

[15]程云龙. 防空导弹自动驾驶仪设计[M]. 北京：宇航出版社，1993.

CHENG Yun-long. Autopilot Design for Antiaircraft Missile [M]. Beijing: Aerospace Publishing Office, 1993.

[16]钱杏芳，林瑞雄，赵亚男. 导弹飞行力学[M].北京： 北京理工大学出版社，2008：64-74.

QIAN Xin-fang, LIN Rui-xiong, ZHAO Ya-nan． Missile Aviation Mechanics[M]．Beijing: Beijing Institute of Technology Press, 2008: 64-74.

Analysis of Control Coupling and Compensation Decoupling Performance for Spinning Missile

JIA Bao1, XUE Lin2, YAN Xiao-yong1

(1.Beijing Institute of Electronic System Engineering, Beijing 100854, China;2.The Second Research Academy of CASIC, Beijing 100854, China)

Abstract:The actuator kinetics result in the control coupling in spinning missile. The transfer function matrix of the equivalent actuator is derived in quasi-body coordinate system. Aiming at the cascade compensation decoupling method, the relation among rotating frequency, input signal frequency and the compensation angle arestudied. The result indicates that the coupling degree will reach the minimum when the compensation angle is optimal. This method can realize the static decoupling only when the control signal frequency is low. There is overcompensation phenomenon when signal frequency is high, and it will reduce the decoupling performance. The upper bound of the compensation angle changes with the rotational speed, so the compensation angle must be revised online to avoid overcompensation phenomenon.

Key words:spinning missile; control coupling; equivalent actuator; diagonal dominance; compensation decoupling; optimal compensation angle

中图分类号：TJ765.1

文献标志码：A

文章编号：1009-086X(2015)-02-0047-07

doi:10.3969/j.issn.1009-086x.2015.02.009

通信地址：100854北京市142信箱30分箱E-mail：abao19881211@163.com

作者简介：贾宝(1988-)，男，山西晋城人。博士生，研究方向为飞行器总体设计。

基金项目：有

* 收稿日期：2014-11-06；
修回日期：2014-12-08