数据链中基于分层博弈的联合控制*



数据链中基于分层博弈的联合控制*

赵雷鸣1,樊雷2,刘昊1，贺刚1，方小强3

(1.海军装备研究院， 上海 200036； 2. 空军工程大学 训练部，陕西 西安 710051；

3. 中国人民解放军91230部队，福建 福州 350000)

摘要：机间数据链通信系统中，节点间具有多种业务功能及大数据量战场信息传输的需求，因此需要对各节点传输速率和发射功率进行控制。针对此，提出基于博弈论的分层联合控制方法，采用了组合代价函数的形式，该方法有效地解决了数据链系统中传输速率与发射功率的联合最优化问题，减少了网络的功率消耗，提升了节点间数据传输速率，满足了机间数据链不同业务的不同速率要求。仿真结果表明，提出的分层联合控制算法能使功率与速率达到联合最优，同时具有快速收敛的特性，有效地提升了机间数据链的低截获能力和抗干扰特性。

关键词：博弈论；数据链系统；功率与速率联合控制；低截获；抗干扰

0引言

在信息化作战中，联合作战是现代战争的主要作战形式，数据链系统是一体化联合作战的“神经中枢”[1]。机间数据链(intra-flight data link，IFDL)系统中，要求共享的战场信息数据量具有很大的不同，既有敌我瞬时态势、燃料、武器配置等小数据量的信息，同时还有图像等数据量较大的信息，而不同的业务对传输速率和QoS要求不同，进一步提高数据链的使用性能和抗干扰能力需要高速、高效、可靠的数据传输能力[2]，因此，需对数据链系统进行功率和速率联合控制。

为提高系统容量和频谱利用率，Sampath[3]提出了联合功率控制与速率分配技术。文献[4]提出了发射功率和传输速率联合分配的策略，旨在追求系统资源的全局最优化，其着重在于对发射功率资源的优化上，存在缺少对速率与功率进行联合最优化的不足。文献[5-7]同时考虑发射功率和速率为效用指标，定义传输速率同发射功率的比值为效用函数。文献[8-9]研究了系统整体性能，使系统整体效用最大化。

由以上文献可知，对速率与功率的联合控制实际上就是采用2种效用函数分别处理速率和功率控制问题，进而对2种效用函数进行联合优化。本文针对机间数据链传输大数据量信息及最大化系统容量问题，提出了采用分层联合优化速率和功率控制效用函数的方法，证明了两种效用函数纳什均衡点的存在性和唯一性，给出了具体的联合控制算法。最后通过仿真验证了算法的优良性能。

1系统模型

考虑一个数据链通信系统，系统由N个节点组成。各节点i(i=1,2,…,N)的发射功率范围是[0,pmax]，传输速率范围为[0,rmax]，采用的是AWGN信道，σ2为接收机背景噪声；W为扩频带宽；Ri为节点i的传输速率；G=W/Ri为通信系统内的扩频增益；于是得到接收节点的SIR可表式为

式中：hi和pi分别为第i个节点的信道增益和发射功率。

节点i收到的其他节点的干扰为

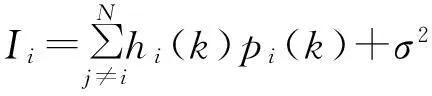
(2)

2分层博弈功率和速率联合控制

2.1效用函数和代价函数

编队内各节点的目标是在速率和功率约束内，使自身的收益最大。采用分层博弈的思想，第1层博弈对传输速率分配最优化，得到均衡速率值；第2层博弈采用第1层博弈得到的最佳传输速率值用以计算相应的最优发射功率。

第1层传输速率博弈中，定义净效用函数G1为

βilg(ri-ri-min)-λri}，

(3)

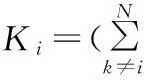
第2层博弈为功率控制博弈，效用函数为

ui(pi,p-i)=λiarctan(1+γi).

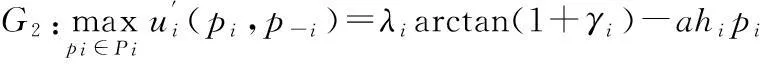
(4)

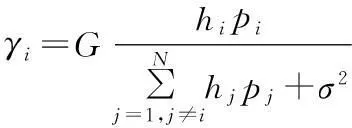
2.2分层博弈模型纳什均衡点的存在性和唯一性

在基于博弈论的联合功率与速率控制中，每个节点都同时在其策略空间中选择相应的值来优化效用函数。节点i的速率和功率信息更新策略分别为

第i个节点第k次速率控制信息更新：

(5)

第i个节点第k次功率控制信息更新：

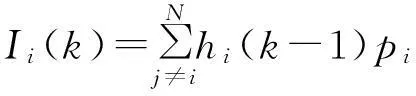
(6)

以下分别证明基于动态博弈模型下的速率及功率纳什均衡点的存在性和唯一性，要证明博弈过程存在纳什均衡点，只需证明博弈模型满足以下2定理：

定理2如果1个静态博弈满足下面两个条件，那么此博弈一定存在纳什均衡：

1) 策略空间是欧氏空间的1个非空的、闭的、有界的凸集；

2) 效度函数在其策略空间上连续，且为拟凹函数。

定理3由文献[10-12]，Yates证明如果在算法中满足p(k+1)=f(p(k))的一个固定点存在，并且f满足以下的3个条件：

1) 正性：f(p)≥0；2)单调性：P≥p′⟹f(p)≥f(p′)；3)可扩展性：∀α≥1;αf(p)≥f(αp)；

那么函数f将是能收敛到唯一的一个固定点的标准向量函数。

(1) 传输速率纳什均衡点存在性和唯一性

在第一层博弈模型中，采用的净效用函数

βilog(ri-ri-min)-λri}，

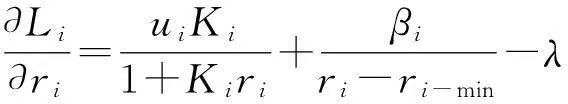
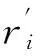
(7)

(8)

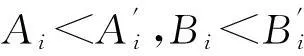
(9)

所以单调性得证。

对于扩展性，设任意η>1，定义：

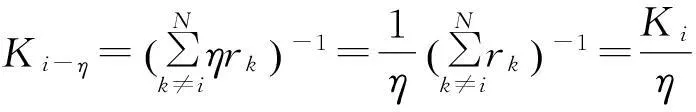
(10)

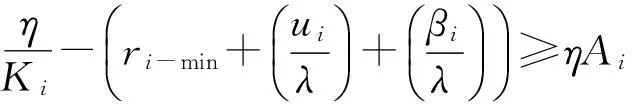
(11)

(12)

则可得：

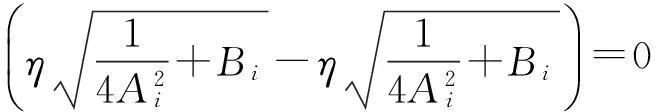
(13)

所以该博弈模型具有扩展性。

通过以上分析，证明了此速率控制博弈模型存在纳什均衡点，数据链通信系统中各节点能够在博弈中实现传输速率的最优化，最终达到最佳传输速率。

(2) 发射功率纳什均衡点存在性和唯一性

在第2层博弈模型中，采用的净效用函数：

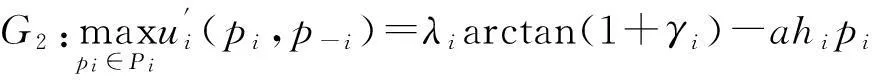
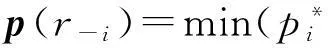
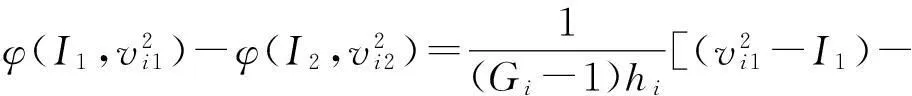
(14)

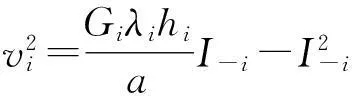
(15)

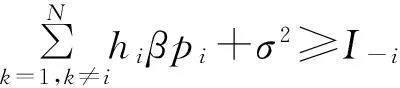
(16)

于是有：

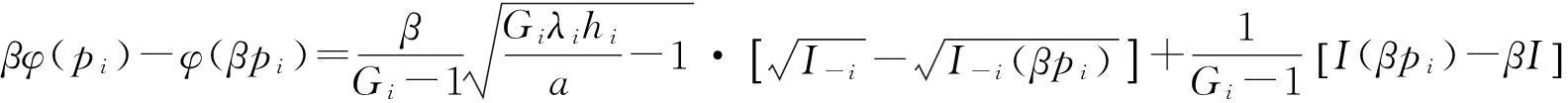
利用式(15)，(16)，上式可演变为

(17)

即可证得其具有可扩展性。

通过以上推导，证明了此博弈功率控制模型存在纳什均衡点，数据链通信系统中的各节点在博弈中能够使自身效用最大化，最终达到最佳发射功率。

3算法仿真及结果分析

3.1功率更新算法

基于博弈的联合功率与速率控制流程如图1所示。迭代更新步骤具体描述如下。

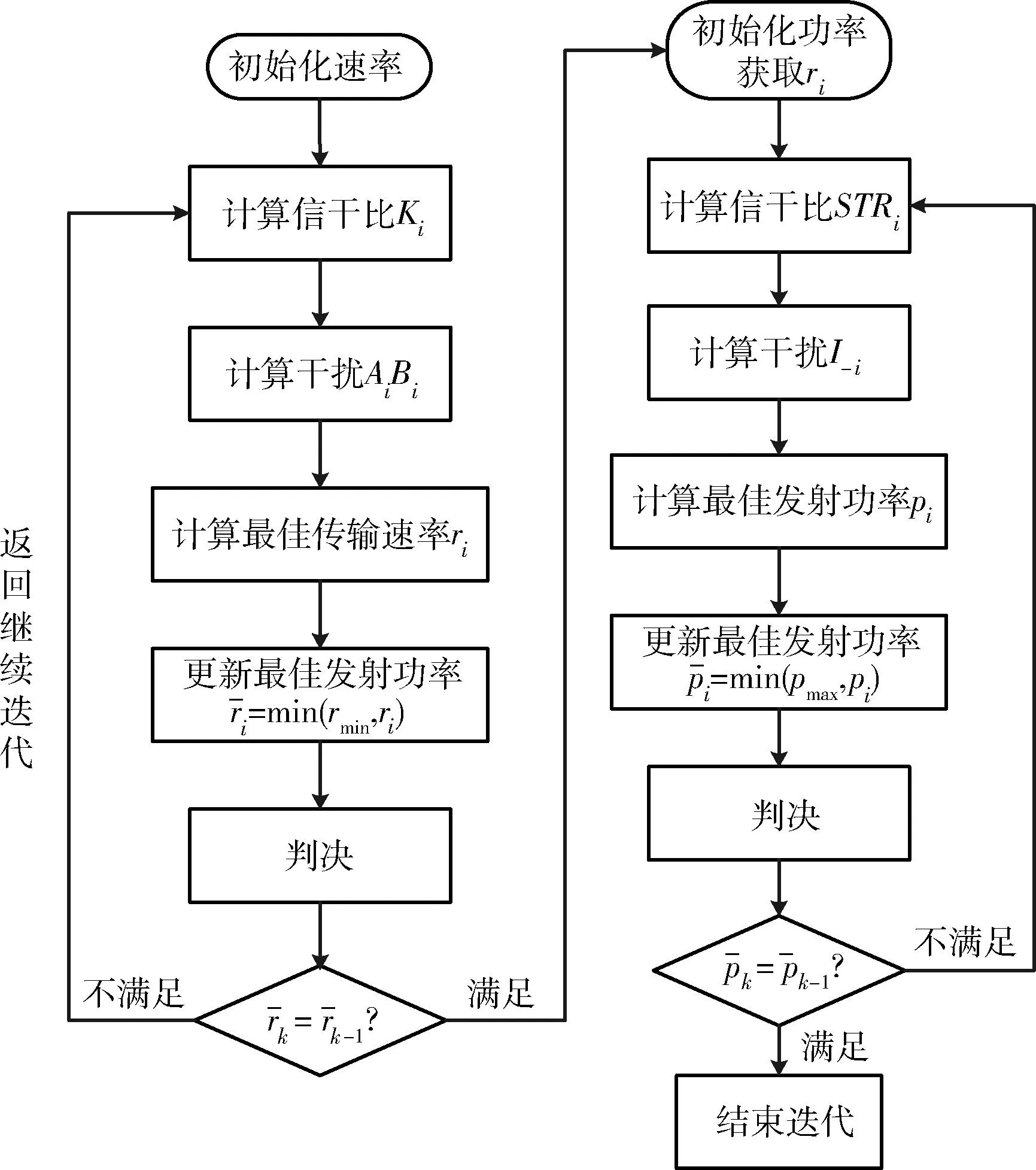
图1　联合功率速率控制流程图Fig.1　Flow chart of joint control of power and rate

第1层速率控制迭代步骤：

步骤1：初{WTBX始化。给节点设置初始值，使r(t=0)=r,r∈r[rmin,rmax]，同时给迭代次数k赋初始值使k=0；

步骤2：当k=k+1时，求出本次迭代的最佳传输速率值；

步骤3：如果r(k)=r(k-1)，则停止迭代，所得到的传输速率值即为纳什均衡速率值，否则返回步骤2，继续迭代到纳什均衡点。

步骤4：将得到的所有节点的最佳传输速率值传送到第2层功率控制博弈中。

第2层功率控制迭代步骤：

步骤2：当k=k+1时，求出本次迭代的最佳发射功率值；

步骤3：判决终止迭代。如果p(tk)=p(tk-1)停止，即为纳什均衡发射功率向量p(tk)，否则使k=k+1，返回步骤2，直到得到均衡解。

3.2仿真结果分析

针对该算法采用Matlab进行仿真实验。仿真设定一个作战编队内有5架战机均匀分布在半径为200 km的区域内，与预警机的距离分别为：dist=[150,170,180,190,200]km。第一层博弈G1为速率控制，第2层博弈G2为功率控制。参数如表1中所示。

表1　联合功率与速率控制仿真参数

图2所示为基于博弈的联合功率与速率控制算法达到均衡的最佳速率与最小数据传输速率的对比图。从图中可以看出，所有节点在纳什均衡点处，所达到的最佳传输速率远大于最小数据传输速率。这说明基于博弈的联合功率与速率控制算法能为数据链系统内各节点提供较高的数据传输速率，并且距离接收端较远的节点也能达到较高的数据传输速率，能确保节点业务的公平性。

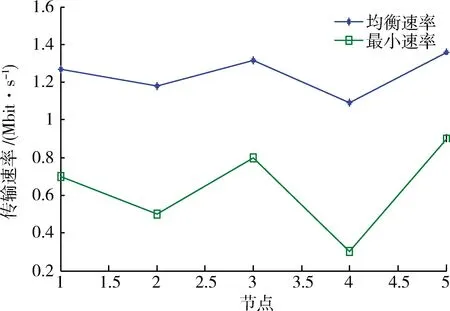
图2　各节点均衡传输速率Fig.2　Equilibrium transmit speed of nodes

图3所示为节点在博弈过程中达到均衡速率的迭代收敛曲线，其中每条曲线代表一个节点数据传输速率随迭代次数的更新情况。图4所示为节点在博弈过程中达到均衡时的最佳发射功率收敛曲线，每条曲线代表一个节点数据发射功率随迭代次数的更新情况。从图中可以看出，节点经过5次左右的迭代运算就能收敛到纳什均衡点处，获得最大效用的传输速率，相应地，节点经过16次左右的迭代运算能达到均衡的发射功率来支持最优传输速率。

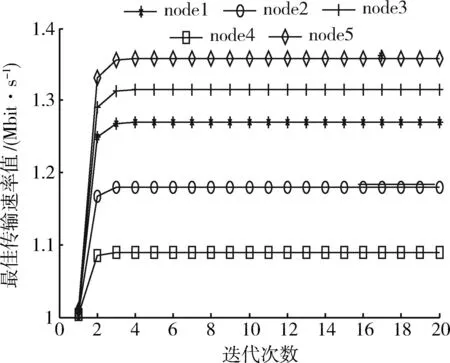
图3　各节点速率收敛曲线Fig.3　Speed convergence curve of nodes

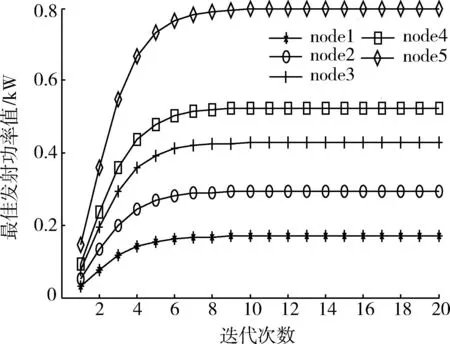
图4　各节点发射功率收敛曲线Fig.4　Transmit power convergence curve of nodes

图5所示为基于博弈的联合功率控制算法得到的SIR收敛曲线，其中每条曲线代表一个节点在更新过程中SIR的变化情况。从图中可以看出各节点在经过15次左右的迭代后达到均衡值，此时距离基站较远的节点所获取的效用比较近的节点要高，体现了算法的公平性。

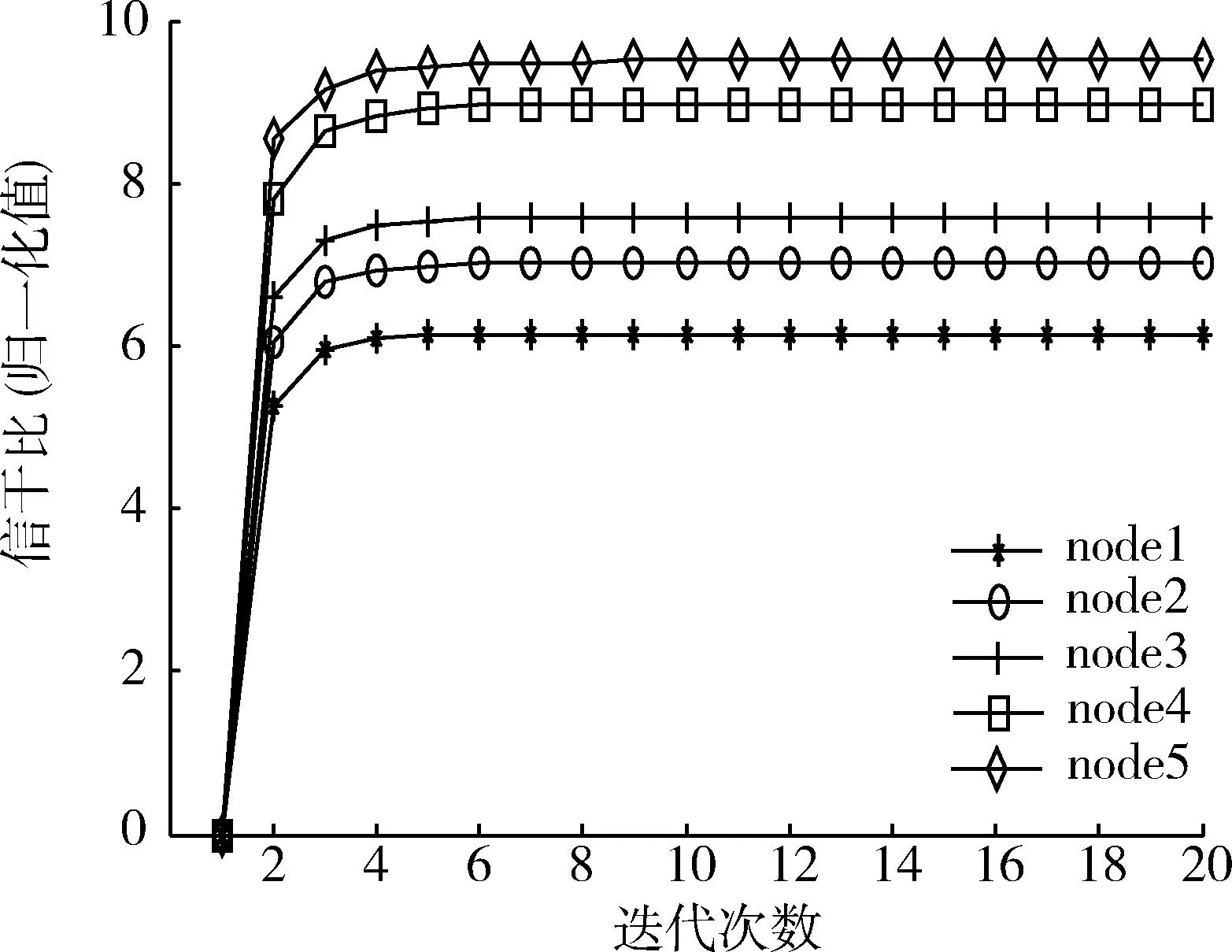
图5　各节点信干比收敛曲线Fig.5　SNR curve of nodes

4结束语

本文以机间数据链为背景，研究了提升数据链系统通信性能的策略，分析了在系统中引入速率与功率联合控制的必要性，建立了相应的系统模型，提出了基于博弈论的分层联合控制算法，解决了速率与功率联合最优化问题，证明了该博弈模型纳什均衡解的存在性和唯一性。并采用Matlab仿真工具对算法进行了性能仿真，对仿真结果进行了分析。仿真结果显示，采用分层博弈的联合控制算法后，数据链系统中各节点能以较低的发射功率获得较高的传输速率，并且具有较好的收敛性能，有利于数据链对大信息量的数据传输，同时最大化系统容量。

参考文献：

[1]谭志强, 徐军. Link11 数据链性能仿真分析[J]. 舰船电子对抗,2011,34(5):81-84.

TAN Zhi-qiang, XU Jun. The Performance Simulation Analysis of Data-Link11[J]. Warship Electronic warfare，2011, 34(5): 81-84.

[2]朱振宇, 林菡, 殷璟.数据链抗干扰技术探讨[J]. 中国水运，2008,16(8): 151-153.

ZHU Zhen-yu, LIN Han, YIN Jing. Anti Interference Technology of Data-Link[J]. China Waterway，2008,16(8):151-153.

[3]SAMPATH A,KUMAR P S，HOLTZMAN J M. Power Control and Resource Management for a Multimedia Wireless System[J]. Proc. IEEE PIMRC’95，1995, 12(3): 21-25.

[4]Yosef Alayev,CHEN Fang-fei, HOU Yun. Throughput Maximization in Mobile WSN Scheduling with Power Control and Rate Selection[C]∥IEEE International Conference on Distributed Computing in Sensor Systems，2012, 5(3): 33-40.

[5]Enzo Baccarelli, Nicola Cordeschi, Tatiana Patriarca. Jointly Optimal Source-Flow, Transmit-Power, and Sending-Rate Control for Maximum-Throughput Delivery of VBR Traffic over Faded Links[C]∥IEEE Transactions on mobile computing, 2012, 11(3):390-401

[6]Parag S Khairnar, Neelesh B Mehta. New Insights into Optimal Discrete Rate Adaptation for Average Power Constrained Single and Multi-Node Systems[C]∥IEEE Transactions on wireless communications，2012, 11(2): 537-543.

[7]Mohammad Mirtavoosi Mahyari, Mohammad R Shikh-Bahaei. Joint Optimization of Rate and Outer Loop Power Control for CDMA-based Cognitive Radio Networks[C]∥International Conference on Computing, Networking and Communications, Cognitive Computing and Networking Symposium，2012, 6(4) :392-396.

[8]ZHOU Shan,WU Xin-zhou,YING Lei. Distributed Power Control and Coding-Modulation Adaptation in Wireless Networks using Annealed Gibbs Sampling[C]∥The 31st Annual IEEE International Conference on Computer Communications: Mini-Conference. 2012, 7(6) :3016-3020.

[9]Shoya TAKEBUCHI, Takuto ARAI. A Novel Clipping and Filtering Method Employing Transmit Power Control for OFDM Systems[C]∥IEEE Wireless Communications and Networking Conference: PHY and Fundamentals，2012, 7(3): 221-225.

[10]YATES R D. A Framework for Uplink Power Control in Cellular Radio Systems[J]. IEEE Journal on Selected Areas in Communications，1995, 13(7): 1341-1347.

[11]BACCI G, LUISE M. A Game-Theoretic Perspective on Code Acquisition in CDMA Wireless Systems[C]∥In Proc. IEEE Conf. Communication, Cape Town, South Africa, 2010, 5(1): 1032-1036.

[12]JI Hong-bin,HUANG Ching-yao. Non-Cooperative Uplink Power Control in Cellular Radio Systems[J]. Wireless Networks，1998, 4(2):233-240.

Joint Control Based on Game-Theory Based on Lamination in Data Link

ZHAO Lei-ming1, FAN Lei2, LIU Hao1, HE Gang1, FANG Xiao-qiang3

(1.Naval Arm Academy,Shanghai 200036,China; 2.AFEU,Training Department,Shaanxi Xi’an 710051, China; 3.PLA,No. 91230 Troop,Fujian Fuzhou 350000,China)

Abstract:In the IFDL(intra-flight data link) system, The node has many kinds of service function and the great data quantity battlefield intelligence transmission demand, Therefore needs carries on the control to various nodes transmission speed and the emissive power. In view of this, This article proposes based on the game theory lamination union control method, Has used the combination price function form, This method solved in the data chain system to transmit the speed and the emissive power union optimization problems effectively, Reduced the network power dissipation, Has promoted the node the data transmission speed, Has satisfied machine the data chain different service different speed request. The simulation result indicated, Proposed the lamination union control algorithm can cause the power and the speed achieved the union is most superior, Simultaneously has the rapid convergence characteristic, Has effectively promoted machine the data chain low interception ability and the antijamming characteristic.

Key words:game-theory; data-link system; joint control of power and rate; low interception; antijamming

中图分类号：TN92

文献标志码：A

文章编号：1009-086X(2015)-02-0096-07

doi:10.3969/j.issn.1009-086x.2015.02.016

通信地址：200036上海市闸北区场中路3519号

作者简介：赵雷鸣(1969-)，男，浙江宁波人。高工，硕士，研究方向为航空电子工程，自动化控制。

基金项目：国家“973”计划(2009CB613306)资助项目

* 收稿日期：2014-01-19；
修回日期：2014-04-22